原子动力学蒙特卡洛程序Open KMC在反应堆压力容器钢缺陷损伤研究中的优化与应用*

尚子豪，商红慧，王东杰，张云泉，贺新福，陈泽华，王 栋，张广婷

（1.太原理工大学大数据学院，山西 太原030024；

2.中国科学院计算技术研究所计算机体系结构国家重点实验室，北京100190；

3.中国原子能科学研究院，北京102413）

1 引言

核能是一种可以大规模使用的工业能源，核能发电具有发电成本较低、发电小时数长、电网接入稳定以及零碳排放等优势。核反应堆压力容器RPV（Reactor Pressure Vessel）是防止放射性物质泄漏的最主要屏障，并且是反应堆中不可拆换的部件，RPV因此成为核电站最关键的部件之一。RPV材料的使用寿命直接决定了核电站的服役寿命，在RPV钢中加入少量的铜能显著提高钢的耐腐蚀性能，同时增加钢的强度和疲劳抗力等。但是，长时间暴露在高能中子辐照场中会导致RPV钢中的铜元素以富铜团簇的形式析出，这些高数量密度的纳米富铜团簇是引起RPV钢产生脆化的主要原因[1，2]。

正常状态下，由于铜的自扩散系数较低，未受到辐照时铜原子基本不能通过扩散聚集而形成团簇，然而高能中子辐照产生的点缺陷会大大提高溶质原子的扩散聚集能力，从而产生原子团簇。利用现代实验技术，如自扩散示踪法、电阻率法和正电子湮没法等[3-5]对点缺陷相关性质的实验测量，可以推断出许多有关缺陷的信息。然而，由于分析方法和仪器分辨率的限制，用这些技术直接观察和研究点缺陷团簇的原子结构和性质很困难。利用计算机模拟的方法可以对各种点缺陷进行深入的研究。

目前对RPV钢的富铜团簇的研究主要集中在辐照注量、辐照温度以及元素含量对其性能的影响，而通过引入点缺陷的方式来观察富铜团簇析出过程的研究较少。动力学蒙特卡洛KMC（Kinetic Monte Carlo）方法[6]可以有效地模拟富铜团簇析出的微观结构演化。许多研究人员致力于开发不同的KMC方法。然而，这类软件多为串行版本，这使得对富铜团簇析出过程的模拟只能在较小的体系中进行，也因此只能引入单个或是少量的点缺陷，限制了模拟的精确程度。为此我们自主开发了可以并行模拟上亿原子体系的Open KMC软件[7]。本文基于Pair势[8]和嵌入原子势EAM（Embedded-Atom Method）[9]，通过引入空位点缺陷的方式，模拟热时效下Fe-Cu二元合金中团簇的析出过程。并对程序中的空位点缺陷选取问题进行了计算优化，通过多组测试验证了优化算法的正确性和有效性，同时对优化后的程序做了大规模并行模拟的性能分析。

2 程序优化

2.1 基于空位跃迁的KMC方法

KMC模拟方法是一种通过构造随机过程来模拟体系长时间演化的方法。经典的原子动力学蒙特卡洛AKMC（Atomic Kinetic Monte Carlo）方法[10]利用晶格点阵来映射原子与格点的位置关系，应用于提供控制微观系统演化的精确解。α-Fe的晶格为体心立方（bcc）结构，空位跃迁事件被认为是空位与其周围第1近邻原子的交换。图1分别给出了bcc晶格中心原子的第1、第2和第3近邻原子（晶格边长为2）。模拟通常包括4个步骤：（1）计算列表中空位的跃迁概率；（2）计算时间增量；（3）执行空位跃迁，增加时间；（4）是否达到时间阈值，若达到则退出，否则循环执行以上步骤。

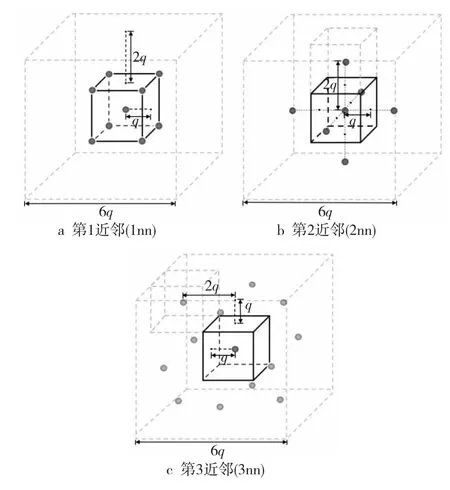
Figure 1 Three kinds of nearest neighbors for a bcc lattice body center atom图1 bcc晶格体心原子的三重近邻

第1步根据当前状态计算空位可能发生的跃迁事件X的概率，这个概率实际上并非真正意义上的0～1的概率，而是一种频率，其计算方式如下所示：

其中，Γ0代表尝试频率，尝试频率被设置为6×1012Hz，k是玻尔兹曼因子，T是绝对温度，EXa表示事件发生需要的激活能。考虑到计算时间和结果精度，我们采用环境相关模型[11]，得到了满足式（2）所示的平衡规则的激活能EXa：

其中，EX0表示参考激活能，仅取决于与空位交换位置的原子的化学性质。本文中使用的包括Fe：0.65 eV，Cu：0.56 e V。Ei和Ef分别表示空位跃迁前后系统的总能量值。

第2步采用驻留时间算法[12]计算时间增量，它与所有可能发生的事件频率之和的倒数成正比，以便将事件的传播与每个独立事件相关联。计算公式如式（3）所示：

其中随机数r∈（0，1）用于选择事件。

第3步是依据概率随机确定空位的跳跃方向，发生跳跃并更新周围原子的能量和跃迁概率。同时，在模拟时间上累积时间增量Δt。最后一步，重复上述步骤，直到模拟时间达到预设阈值。

在计算第1步中的能量时，原子间相互作用势采用Pair势能模型[8]或EAM势能模型[9]，Pair势由于其简洁的形式、较小的计算量和有效的计算结果，在原子层次的计算机模拟中得到了广泛的应用。Pair势中原子间的相互作用最远只考虑到第2近邻位置。组成系统的所有实体间的化学相互作用可以通过式（4）描述：

当方程中a等于1或2时，分别对应于第1或第2近邻相互作用。Va表示空位，b为Fe-Fe键的数目，c为Va-Va键的数目，l为Fe-Va键的数目，m为Fe-Cu键的数目，n为Va-Cu键的数目，p为Cu-Cu键的数目。

EAM势中原子间相互作用由Pair势和多体嵌入势共同贡献，并且至多考虑到第3近邻。其势能计算方式如式（5）所示：其中，μ和v为原子表示，F（）为多体嵌入能函数，ρμ为μ处插值的总电子密度。相比于EAM势能模型，Pair势能模型的局限性在于缺乏多体嵌入势能，不能考虑局部环境的影响。此外，Pair势能模型需要通过实验或热力学数据仔细调整。本文所用的Pair势能模型参数取自文献[13]，可以得到接近EAM模型的结果，也可以推广到更复杂的多元合金研究当中。

2.2 计算优化

KMC算法中模型的最主要部分包括跃迁概率和系统能量的计算。如前面提到的，在模拟的第3步空位发生跃迁之后，需要对该空位周围原子的能量和跃迁概率进行更新。相当于在下次空位跃迁事件发生之前，我们要对体系内所有受到上一次跃迁影响的空位进行更新。以往的KMC版本是将上次发生跃迁的原子附近理想半径下的全部空位作为需要被更新的对象。事实上，这些空位当中有很多因为距离较远，而并没有受到上次跃迁事件的影响，导致模拟过程出现了很多冗余的模拟计算。因此，如何选取需要被更新的空位成为一个关键问题。

被更新空位的选取与采用的势能函数的计算方式有关。对于Pair势能模型来说，原子间的相互作用最远考虑到第2近邻位置。某一空位是否受到上次跃迁影响取决于这个空位的第1近邻原子是否与上次发生跃迁的原子存在相互作用。如果能找到发生跃迁的原子可以影响到的最远距离的空位位置，并将这个最远距离作为截断半径，每次跃迁事件结束后只更新截断半径以内的空位，就能避免大量的冗余计算。

截断半径的推导过程在三维坐标系中完成。假设发生跃迁交换的原子分别为i和j，并在坐标系中固定i和j的位置坐标。确定Pair势能模型下最远处需要被更新的空位位置可以分为下面3个步骤：（1）找到j原子附近2层近邻内的全部原子并记录坐标；（2）分别计算这些原子与i原子的距离，找到其中一个与i原子距离最远的原子记为s；（3）记录s原子的8个1nn近邻原子坐标，并找到其中与i原子距离值最大的对应原子记为k。其中近邻中的nn代表nearest neighbor，表示第几近邻的含义。通过以上3步得到最远处需要被更新的空位k位置。所有原子间位置关系如图2所示，将立体图展开得到图3中的三视图，其中晶格边长为2。

Figure 2 Stereogram of Pair truncation radius derivation图2 Pair截断半径推导立体图

Figure 3 Three views of Pair truncation radius derivation图3 Pair截断半径推导三视图

Table 1 Nearest neighbor distance comparison table表1 近邻距离对照表

通过相同的思路，可以确定EAM势能模型下空位更新的截断半径。与Pair势能模型的区别在于，EAM势能模型的原子间相互作用考虑到第3近邻位置，因此在寻找空位k步骤的第1步里要找到j原子附近3层近邻内的全部原子并记录坐标，接着执行相同的第2步和第3步。计算出的EAM势能模型下的截断半径dEAM=6。在不改变原子间相对距离的条件下能够确定3种情况的原子间位置关系，这里给出其中一组所有原子的位置关系如图4和图5所示。

Figure 4 Stereogram of EAM truncation radius derivation图4 EAM截断半径推导立体图

Figure 5 Three views of EAM truncation radius derivation图5 EAM截断半径推导三视图

算法1为空位选取优化算法的伪代码实现。

算法1空位选取优化算法

输入：lattice_constant，vacant，input_i，events，d。

输出：空位更新后的系统。

1.unitdis←2/lattice_constant；/*晶格常数转换因子，用于获取原子坐标时将晶格常数转换为2，从而与截断半径的推导过程关联起来*/

2.i←vacant[input_i]；//获取发生跃迁事件的空位i

3.proball←sum（events[i].propensity）；/*空位i对应的事件列表内所有跃迁事件的概率和*/

4.ifproball＞0then

5.threshhold←proball*random（）；

6.j←threshhold；//选取发生跃迁交换的原子j

7.do_jump（i，j）；//发生跃迁事件

8.endif

9.d1，d2←0，0；

10.forkinvacantdo

11.round（i，j，k）；/*获得跃迁原子i，j和查询空位k的实际坐标*/

12.round（i，j，k）*unitdis；/*获得晶格常数转换为2后各原子对应的坐标*/

13.d1←compute_linedis（i，k）；/*计算i与k的距离d1*/

14.d2←compute_linedis（j，k）；/*计算j与k的距离d2*/

15.ifd1≤dord2≤dthen

16.site_propensity（k）；/*更新空位k的跃迁概率*/

17. endif

18.endfor

在403规模的盒子中进行模拟，分别验证Pair势能模型和EAM势能模型下优化算法的正确性。首先用无优化的程序，即不考虑截断半径，每次跃迁结束后都对全局空位进行更新的方法对不同空位浓度进行了7组测试，并得到了系统的初始能量和末态能量。接着用空位选取算法优化后的程序在相同的输入环境下同样进行7组测试，并得到了算法优化后的系统始末能量，2种模型下的能量对比分别如表2和表3所示。

Table 2 Comparison of system energy before and after Pair potential model optimization表2 Pair势能模型优化前后系统能量对比

Table 3 Comparison of system energy before and after EAM potential model optimization表3 EAM势能模型优化前后系统能量对比

将2种模型无优化时的末态能量画成曲线的形式，优化后的末态能量画成点的形式得到图6，可以看出，优化后的点均落在无优化时的曲线上面，即2种模型在初始能量相同的情况下，不同空位浓度下算法优化后的末态能量均与无优化时的末态能量保持一致，优化后的程序并没有影响模拟的演化进程，保证了算法优化后模拟结果的正确性。

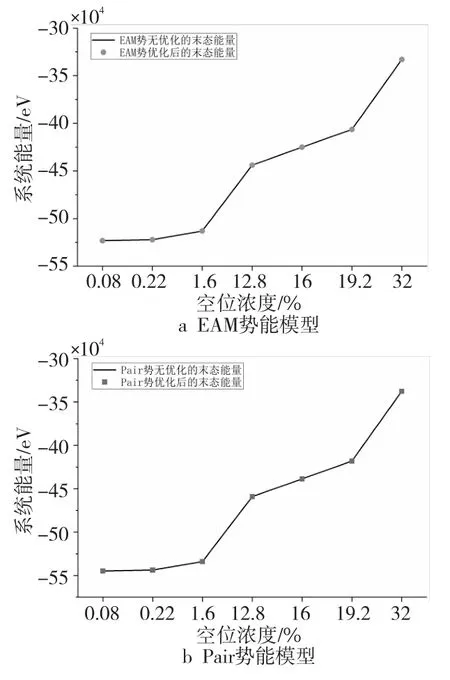
Figure 6 Final energy comparison before and after optimization of two models图6 2种模型各自优化前后末态能量对比

接着为了测试优化算法的效率提升，本文分别对Pair势能模型和EAM势能模型在无优化和空位选取优化算法下进行了不同空位浓度的测试，并统计了模拟用时。另外，本文选用了动力学模拟软件Lakimoca[9]当中的截断半径数值（d=10.5）进行空位选取，同样对2种势能模型下不同空位浓度的体系进行测试并得到相应的模拟用时。最终得到了如图7和图8所示的效率提升对比图。由图7和图8可知，随着空位浓度的增加模拟用时越来越长，EAM势能模型下的无优化模拟用时大幅度多于空位选取优化的模拟用时，当空位浓度为1.6%时，无优化的模拟用时最高达到了空位选取优化模拟用时的26.75倍。同时，Lakimoca空位选取方式下的模拟用时相比于无优化时有很大的减少，但当空位浓度达到1.6%时，仍有超出空位选取优化一倍的时间开销。Pair势能模型下3种方法的模拟用时与EAM势能模型下的用时变化具有相同的增大趋势，但由于Pair势的计算方式本身比EAM势更加简单，因此在相同空位浓度环境下比EAM势用时更少。显然，无论是Pair模型还是EAM模型，空位选取优化算法下的模拟都具备更高的效率，尤其当空位浓度升高时，能够避免很大一部分由于空位更新带来的冗余计算，使得模拟花费的时间开销进一步减小。

Figure 7 Comparison of Pair potential efficiency improvement图7 Pair势效率提升对比

Figure 8 Comparison of EAM potential efficiency improvement图8 EAM势效率提升对比

2.3 性能分析

为了得到优化后的程序在大规模并行模拟当中表现出的性能数据，本文从强可扩展性和弱可扩展性2方面对程序进行了测试与分析。测试环境的相关配置参数如表4所示。

Table 4 Test environment related parameters表4 测试环境相关参数

强可扩展性的测试是指固定模拟体系规模，只增加CPU核数，并观察加速比和并行效率的变化。本文将模拟体系规模固定为10003，初始化模拟时间为t=1×10-4s，并设置用来控制自适应同步算法的时间间隔参数nstop=10（nstop参数为每个子域设定一个可发生事件的平均值，结合所有子域发生事件的概率均值来计算子域的时间增量）。在溶质Cu浓度为1.34%，空位浓度为0.08%，模拟温度T=573 K的体系环境中，将CPU核数从1 000增加到5 000，分别对Pair势和EAM势进行算例测试，得到各组算例的模拟用时，并以1 000核算例为基准计算了其他各组算例的加速比和并行效率，测试结果分别如表5和表6所示。

Table 5 Test results of Pair potential strong scalability（Scale of simulation system：10003）表5 Pair势强可扩展性测试结果（模拟体系规模：10003）

Table 6 Test results of EAM potential strong scalability（Scale of simulation system：10003）表6 EAM势强可扩展性测试结果（模拟体系规模：10003）

2种势能模型并行效率的变化过程如图9所示。结合表5和表6可以看出，当CPU核数从1 000增加到3 000时2种势能模型的模拟用时下降可观，呈现出不错的加速比和并行效率。当CPU核数进一步增加到5 000时加速比增长速度继续放缓，其中EAM势在5 000核时的加速比已经小于4 000核时的加速比，并且整体的并行效率也呈现下滑。这是因为CPU核数增加使得进程间的通信工作量变大，通信时间开销逐渐占有更高比重，使得并行效率呈现下滑的趋势。5 000核的测试算例中，Pair势的并行效率为52%，EAM势的并行效率为49%，在大规模体系并行模拟中总体表现出良好的强可扩展性。

Figure 9 Parallel efficiencies of strong scalability of two models图9 2种模型的强可扩展性的并行效率

弱可扩展性的测试是指保持单个CPU核的工作负载不变，在增大模拟体系规模的同时以相同的比例增大CPU核数，并观察并行效率的变化过程。弱可扩展性的测试采用与强可扩展性测试当中相同溶质浓度、空位浓度和模拟温度的体系环境，将模拟体系规模从2003逐渐增大到10003，同时保持CPU核数以相同比例增长，分别对Pair势和EAM势进行测试，得到了各组算例的模拟用时，并以2003模拟规模的算例为基准计算了其他各组算例的并行效率，测试结果分别如表7和表8所示。

Table 7 Test results of Pair potential weak scalability表7 Pair势弱可扩展性测试结果

弱可扩展性测试中2种势能模型的并行效率随CPU核数增加的变化过程如图10所示。结合表7和表8可以看出，随着模拟体系规模和CPU核数的同比例增加，模拟用时并没有保持相对恒定而是逐渐增加，通信时间增加带来的负面影响变大。在5 000核测试当中Pair势的并行效率为0.60，EAM势的并行效率为0.68，仍保持着较好的并行性能，因此程序在大规模体系并行模拟中总体具有良好的弱可扩展性。

Table 8 Test results of EAM potential weak scalability表8 EAM势弱可扩展性测试结果

Figure 10 Parallel efficiencies of weak scalability of two models图10 2种模型的弱可扩展性的并行效率

3 数值模拟与分析

模拟采用自主开发的Open KMC软件，相比于传统的原子动力学蒙特卡洛（AKMC）串行方法的效率在大规模仿真中会受到模拟时间过长和内存溢出的限制，Open KMC在AKMC的基础上将模拟体系分解成多个进程，同时将每个进程的工作负载划分为更细粒度的扇区，以此避免进程间的边界冲突。利用众核处理器，Open KMC可以实现和加速上亿个原子的大规模KMC并行仿真。本文在文献[7]的Open KMC程序基础上实现了2.2节中的计算优化，在不影响模拟结果的情况下使得模拟速度得到进一步提高，并将优化后的Open KMC程序应用于接下来的大规模并行模拟当中。另外，文献[7]采用Open KMC基于Pair势能模型进行了大规模并行模拟，本文除了采用Pair势能模型外，还将加入模拟结果更为可靠的EAM势能模型做分析和比较。并行模拟所采用的测试环境的各项参数如表4所示。

3.1 并行模拟

首先，构造规模为5003的bcc晶格Fe基体，原子总数为2.5×108。α-Fe的晶格常数为2.855Å。溶剂原子是Fe，溶质原子是占比为1.34%的Cu，体系中引入的空位点缺陷浓度为4×10-4%，模拟温度T=573 K。在保证内存不会溢出的前提下，为了能够充分利用计算资源，本次模拟采用单节点64核进行并行模拟。根据Vincent等人[14]的工作，本文将模拟时间进行了重新标度，从而获得相应的物理时间尺度。其时间标度转换公式如下所示：

在模拟刚开始阶段体系中孤立的Cu原子数目为3 006 580，体系引入的1 000个空位随机分布在并行模拟的64个进程当中。图11显示了Pair势能模型与EAM势能模型下体系内孤立铜原子的下降过程，模拟对应的实际物理时间已经通过式（6）和式（7）缩放为蒙特卡洛模拟时间。由于Pair势能模型下的曲线在模拟初期下降很陡，图11中右上角的小图更好地显示了2种模型在模拟的最早时间内孤立铜原子的变化过程。2种模型体系中孤立Cu原子的数目均在一开始迅速下降，接着下降速度逐渐放缓，最终保持着个位数的下降趋势。显然Pair势相比EAM势的模拟结果仍有差距，但考虑到2种模型下的结果呈现相同的趋势，并且由于Pair势能更小的计算量使得模拟用时大大减少，因此利用Pair势能模型进行数值模拟与分析在多数情况下也是较好的选择。同时，根据本次实验的模拟结果也可以对Pair势能模型参数做进一步的调整，从而使得模拟结果更加能接近EAM势能模型的结果。

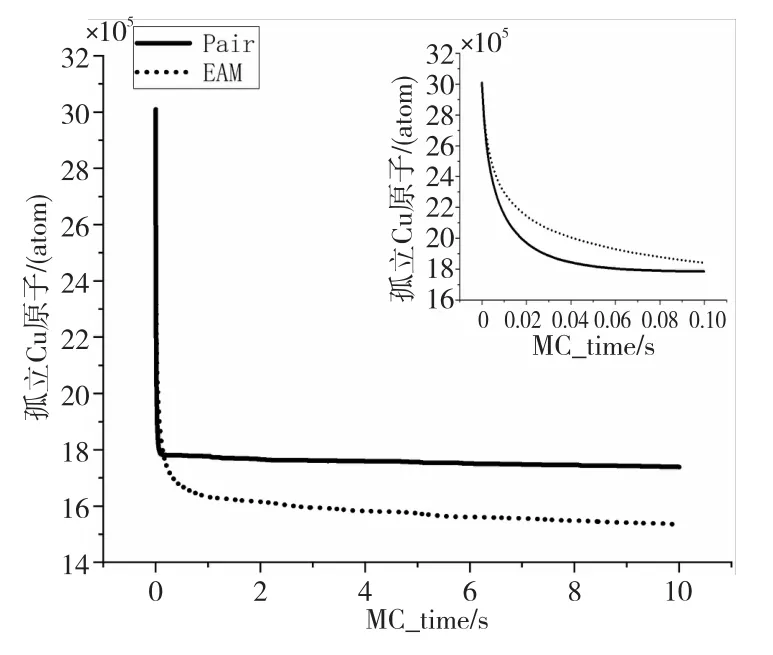
Figure 11 Decline curve of the number of isolated Cu atoms图11 孤立Cu原子数量下降曲线

利用EAM势能模型下的模拟结果对实验现象进行分析。经统计在整个模拟过程的前0.1 s蒙特卡洛模拟时间里，体系内已有超过50%的孤立Cu原子形成了团簇。用时间标度公式换算后相当于Fe-Cu合金服役工作65年。利用粒子可视化软件Ovito对0.1 s蒙特卡洛模拟时间下的形核结果进行输出。此时体系中已经析出大量如图12和图13所示的富Cu团簇和Cu-Va的复合体，其中浅色的圆球代表空位点缺陷，深色的圆球代表Cu原子。

Figure 12 Pure Cu clusters in the system图12 体系内的纯Cu团簇

Figure 13 Cu-Va complex in the system图13 体系内的Cu-Va复合体

为了验证体系中Cu和空位的富集现象，计算了原子间短程有序SRO（Short Range Order）参数值[15]，其中有序参数定义为：

Table 9 SRO value____表9 SRO值

将体系中每帧状态下对应的最大纯Cu团簇尺寸、最大Cu-Va复合体（空位数不少于10）尺寸统计输出如图14所示。因为体系中空位的数量远少于溶质Cu原子的数量，在模拟的前期纯Cu团簇更易形成。但是，随着模拟的进行，空位逐渐聚集并与Cu原子组合形成Cu-Va复合体团簇，复合体尺寸反超纯Cu团簇尺寸，成为了体系内尺寸更大的团簇。这是由于单空位向空位团簇迁移可以使系统能量降低，因此形成更大更稳定的团簇；同时，Cu-Va间的结合能大于Cu-Cu间的结合能，组成的Cu-Va复合体可以进一步降低体系的能量，这也是Cu-Va复合体团簇在体系中可以稳定存活的主要原因。

Figure 14 Comparison of maximum cluster size图14 最大团簇尺寸比较

在溶质的扩散聚集过程当中综合了空位形成能和迁移能的作用，以往的AKMC模拟大多在体系中只放入一个空位，并且体系的规模都很小，例如1×106个原子。而本文模拟结果表明，当体系中空位数量不止1个时，体系中出现了很多较大的Cu-Va复合体团簇，这说明传统的单空位模拟方案未必合理，我们不能忽略空位增加对团簇形成产生的影响。本文模拟的体系中包含1 000个空位，为了研究空位数量对团簇形成产生的影响，本文在与之前相同的体系环境中分别引入500，800，1 200，1 600和2 000个空位进行了5组对比测试。首先是体系中孤立Cu原子的数目变化曲线对比，如图15所示，可以看出，在沉淀析出过程趋于平稳之前空位数量的增多加快了体系内Cu原子的聚集过程。进一步地，为了研究空位数量对团簇的数量密度和尺寸产生的影响，提取了蒙特卡洛模拟时间0.1 s下各组测试中最大的团簇，发现它们的尺寸均不超过40个原子。

Figure 15 Decline curve of isolated Cu atoms in different vacancy number systems图15 不同空位数量体系下的孤立Cu原子下降曲线

本文假设体系中尺寸≥25个原子的团簇为较大团簇，将各组测试环境中全部团簇（尺寸≥5个原子）的数量密度和尺寸≥25个原子的团簇的数量密度统计输出如图16和图17所示。图16和图17的纵坐标表示单位体积内的团簇数量。可以看到，随着空位数量的增加，体系内总团簇的数量密度相对稳定且处于同一个数量级，没有较大差异。与此同时空位越多，体系内的较大团簇数量密度有明显提高。此时体系内的细小团簇会出现分解，相对较大的团簇通过吸收细小团簇分解出的Cu原子来保持尺寸增长。而空位增多能够促进这种团簇粗化现象，进而形成更多较大尺寸的沉淀。

3.2 实验比较

为了与真实的实验过程进行比较，本文在403的体系下对663 K～773 K的温度进行了一系列热时效模拟。其中溶剂为Fe，溶质为占比1.34%的Cu，引入占比8×10-4%的空位浓度。并与Lê等人[5]的实验结果进行了比较。本文对模拟的演化过程进行了蒙特卡洛模拟时间10 s的跟踪，利用式（6）和式（7）转换得到不同温度下实际演化的物理时间real_time=105s，并分析了这段时间的溶质析出过程。105s对应的蒙特卡洛模拟时间分别为：温度为663 K时tMC_Pair=3.2×10-4s和tMC_EAM=9.53×10-3s；温度为693 K时tMC_Pair=1.3×10-3s和tMC_EAM=3.3×10-2s；温度为733 K时tMC_Pair=7.04×10-3s和tMC_EAM=0.15 s；温度为773 K时tMC_Pair=3.2×10-2s和tMC_EAM=0.59 s。按照式（9）计算沉淀推进系数，其中NX（0）是体系初始化时的孤立铜原子数量，NX（t）是时间t时体系内孤立铜原子的数量，NX（∞）为无穷远处的体系内孤立铜原子数量。

Figure 16 Evolution curve of total clusters number density under different vacancy number systems图16 不同空位数量体系下的总团簇数量密度演化曲线

Figure 17 Evolution curve of number density of clusters with large size（≥25）图17 较大尺寸（≥25）团簇数量密度演化曲线

ζ（t）=（NX（0）-NX（t））/（NX（0）-NX（∞））

（9）

图18显示了4种温度下的Pair势能模型和EAM势能模型分别经历蒙特卡洛模拟时间10 s演化的体系内孤立铜原子的下降过程。本文中NX（∞）选用蒙特卡洛模拟时间10 s时的孤立铜原子数量。将计算后的结果与电阻率测量得到的真实实验值进行了比较，结果如图19所示。

显然，在热时效的模拟过程中，Cu的析出是渐进的。在这一部分工作中，文献[7]中的模拟结果与实验值的对比显示出了很好的吻合程度。而本文中的模拟结果与实验值曲线则有明显的区别。这是由于之前的计算并没有将NX（∞）取为理想的无穷远处的孤立铜原子数量，而是在模拟的体系尚未达到相对稳定的状态时取最后时刻的孤立铜原子数量作为NX（∞）并代入计算，导致计算出的推进因子并不能实际反映模拟过程中的沉淀推进过程。本文中的沉淀推进过程与实验值的偏差来自简化模型的定量偏差，例如系统内只有一种类型的缺陷，即空位点缺陷，以及原子间缺乏长程相互作用。但是，模拟曲线至少可以定性地描述体系随时间增加的演化过程，并且当温度升高时，EAM势能模型的拟合结果与实验值更加接近，在温度为773 K时，所得模拟结果与实验值基本吻合。簇粗化，形成尺寸较大的沉淀。最后，本文计算了4种不同温度下模拟的沉淀推进结果，并与实验值计算出的结果进行了比较，在一定程度上本文的沉淀推进过程与实验结果具有相同的趋势，并且当温度升高时具备更好的拟合效果。

Figure 18 Evolution of isolated Cu atoms in Pair potential model and EAM potential model at different temperatures图18 不同温度下Pair势能模型与EAM势能模型的孤立Cu原子演化过程

Figure 19 Evolution of precipitation advance factor in Pair potential model and EAM potential model at different temperatures图19 不同温度下Pair势能模型与EAM势能模型沉淀推进因子演化过程

4 结束语

本文基于Pair势能模型和EAM势能模型，针对Open KMC软件中原子跃迁事件发生后的空位更新问题进行了算法优化，在保证模拟结果与未优化时一致的情况下，缩短了模拟用时，并且当空位浓度升高时具有更好的效率提升。同时，对优化后的程序做了大规模并行模拟的性能分析，其结果显示程序具备良好的强可扩展性和弱可扩展性。进而利用优化后的Open KMC软件并行模拟了热时效下大规模体系Fe-Cu合金中引入多空位后的团簇析出过程。模拟结果表明：（1）本文方法预测了体系中富Cu沉淀和Cu-Va复合体的析出，并通过计算SRO参数验证了原子聚集现象。（2）统计了体系内最大团簇尺寸的变化过程。发现尽管引入空位点缺陷的数量远小于溶质Cu原子的数量，但体系内形成的Cu-Va复合体相比于纯Cu团簇更易成为体系尺寸更大的团簇。（3）在相同的体系环境下，增大引入合金中的空位数量，可以加快沉淀的析出过程。（4）空位数量的增加不会对体系内总的团簇数量密度产生明显的影响，但是能够促进团