基于自适应BP神经网络的压水堆堆芯换料关键参数的预测方法

王 端，王威策，潘翠杰，王东东

(1.核工业研究生部，北京 102413；2.核工业西南物理研究院，四川 成都 610041;3.中国原子能科学研究院，北京 102413)

压水堆核电站堆芯换料设计与核电厂的经济性和安全性密切相关，一个优选的堆芯装载方案，可较好地展平堆芯功率分布，增加卸料燃耗深度，延长堆芯换料周期，从而提高燃料利用率和核电厂安全性。堆芯优化装载方案的搜索是一项十分费时费力的工作，目前国内工程设计单位通常采用手工搜索的做法。随着中国核电迅速发展，核电运行机组增多，欲在短时间内优选换料方案，换料工程师将承受较大的压力和困难。因此，研发高效实用的堆芯换料设计软件具有很高的工程应用价值和实际意义。

压水堆堆芯换料设计是在众多换料方案中选择最优换料方案，本质上是属于多变量、非线性的动态优化问题，现代数学理论已证明这类问题是NP-难问题[1-2]。目前，国内外已围绕该问题利用各种优化方法开展了大量的研究，主要分为确定性优化方法——线性规划、非线性规划、动态规划、直接搜索、专家系统等[3-4]，以及随机优化算法——模拟退火算法、遗传算法、粒子群算法等[5-10]。但迄今为止，尚无快速搜索出全局最优解的通用方法。其中1个主要的困难是，在每种换料方案下，堆芯参数的取得需调用专用的物理和热工耦合程序，计算量大、耗时多。如果能开发出快速预测压水堆堆芯参数的程序，对于节约最优方案的搜索时间，具有非常重要的意义。

另一方面，核电厂在正常运行和运行瞬变中，堆芯的运行工况处于经常变化的状态(如负荷追随运行)，这些变化导致实际运行中的堆芯状态与装料方案中的计算结果发生偏离，操纵员需及时准确地了解堆芯功率因子等参数状况。因此，研制一种能快速判断压水堆堆芯参数的计算机实时预测程序也是十分必要的。

在20世纪90年代，研究者开始使用各种人工智能算法进行堆芯参数的预测。Kim等[11]开发出了基于BP(back propagation)人工神经网络的高丽一号压水堆堆芯参数预测程序，且相对误差在10%以内,引起了后续研究者的兴趣[12]。BP人工神经网络是一种无反馈前向网络[13]，一般由输入层、隐含层和输出层构成。作为人工神经网络的重要模型之一，BP神经网络能将给定的输入输出数据对中的映射关系经过训练学习得到，对于未学习过的数据依然能做出非常不错的预测，理论上具有实现任何复杂非线性映射功能的特点，因而成为较成功的预测方法。但网络本身存在一些缺点需进一步改进，包括神经元节点数难以确定、传统梯度下降算法效率不高等，这也是本次工作的重点。

综上所述，基于BP神经网络的预测方法能快速准确地获得核电厂堆芯换料关键参数，减少最优换料方案的搜索时间，是一个具有重大研究意义的课题。但传统的BP神经网络存在一些问题，影响了预测的精度。本文基于秦山二期压水堆堆芯参数预测问题，在传统神经网络上引入自适应方法，通过调整学习率、权重和网络节点数，得到优化的网络结构，提高预测精度，旨为人工智能在核工业领域的进一步应用做出探索。

1 BP神经网络原理

1.1 BP算法概述

对于隐含层的第j个节点有：

(1)

(2)

对于输出层的第j个节点有：

(3)

(4)

然后定义1个损失函数E：

(5)

式中，di为输出层第i个节点期望输出。

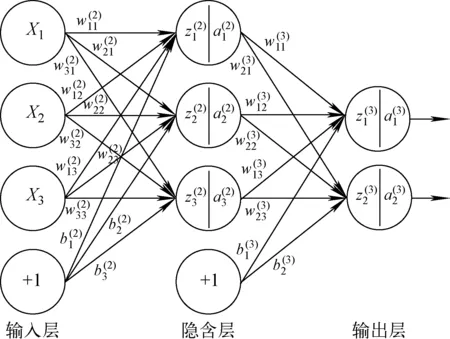
图1 神经网络结构、参数示意图Fig.1 Schematic diagram of neural network structure and parameter

传统的BP神经网络的学习过程就是以降低损失函数E为目标，不断调整输入、输出层的权值w,令期望输出和实际输出靠近的迭代过程。这是一个优化问题，通常采用梯度下降算法来优化权值。梯度下降算法使用如下公式：

(6)

式中：n为迭代次数；ε为固定学习率，ε的取值对算法的收敛性和收敛速度有较大的影响。

1.2 传统BP神经网络特点

传统的BP网络结构简单，工作方式稳定，理论上可实现高精度非线性拟合，对于简单分类、非线性映射、模式识别等问题有一定的应用空间[14]。但传统BP神经网络也有几个较为明显的不足，包括易陷入局部极值、学习率不可调、隐含层节点数难以确定及训练效果严重依赖样本数量等。下面的研究运用了一些优化策略，令网络通过自适应调整一定程度上避免了上述缺陷。

2 秦山二期压水堆实验程序设计与仿真实现

2.1 原始数据集的处理

1) 输入与输出向量的确定

BP神经网络需将原始数据转化为标准的训练集。假设有N个训练样本，则每个训练样本应为Tk=(Xk,Yk)(k=0,1,2,…,N-1)，其中，Xk=[xk1,xk2,…,xki]，Yk=[yk1,yk2,…,ykj]，式中，i、j分别为输入、输出维度。

现有1 000组秦山二期压水堆1/8对称排布的反应堆堆芯数据，是通过方形组件堆芯燃料管理程序系统CMS计算得出，精度较高。每组数据样本由堆芯排布方式与3个堆芯参数(有效增殖因数keff、组件功率峰因子RPF、棒功率峰因子FΔH)组成。输入维度由反应堆堆芯排布决定，输出维度为堆芯参数。反应堆堆芯排布如图2所示。图中每个方形位置代表1个燃耗组件，燃耗组件分为A、B、C、D 4种，分别代表新燃料燃耗组件、1次、2次、3次燃料燃耗组件，燃耗组件不可为空。共有21个组件，所以输入维度为21。

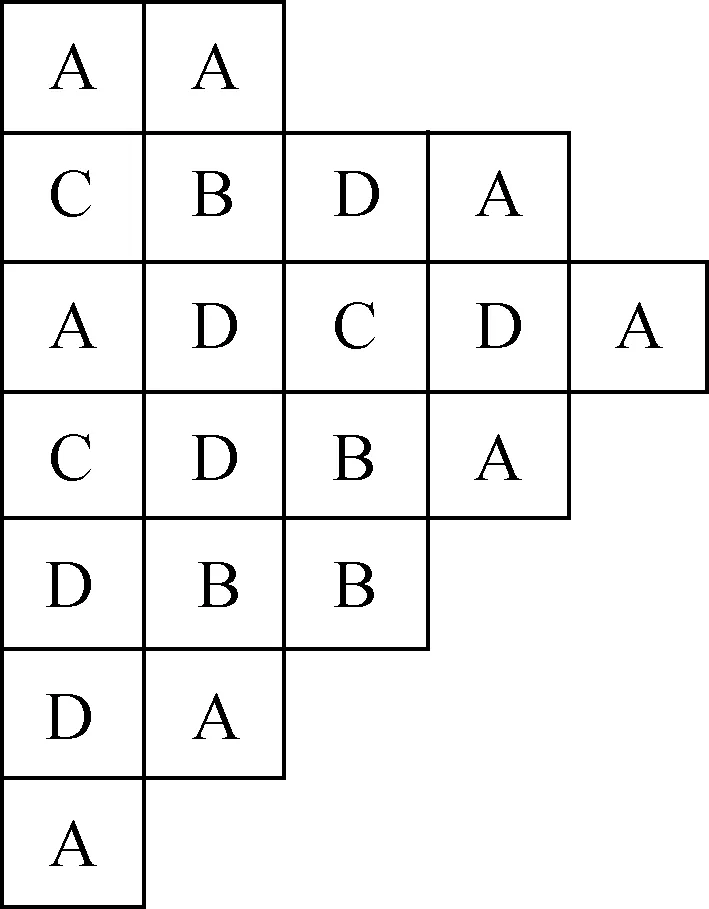
图2 堆芯燃耗组件排布示意图Fig.2 Schematic diagram of core burnup assembly layout

将装载方式转换为向量。为保证归一化以及形式上的对称，在[-1,1]取等间距的4个点，用-1表示A，-1/3表示B，1/3表示C，1表示D，组件读入顺序为先从上到下，再从左到右。以图2为例，输入向量X=[-1,1/3,-1,1/3,1,1,-1,-1,-1/3,1,1,-1/3,-1,1,1/3,-1/3,-1/3,-1,1,-1,-1]。为保证精度，训练时分别用3套独立的网络预测3个参数，因此输出维度为1。

2) 数据集分类

原始数据样本的排布具有一定的规律性，局部特征较为明显。为避免网络过多地学习局部特征(噪声)，每次训练开始前均对1 000个数据随机打乱顺序，得到1个重新随机排列的数据集A，A=[[X0,Y0],[X1,Y1],[X2,Y2],…,[X999,Y999]]。

取A的前970组数据构成1个训练集T，最后30组构成测试集B。再抽取T中的前30组数据构成1个对照集C。网络训练过程中只有训练集T参与网络训练，测试集B只用于预测和误差分析。对照集C参加训练，样本数量与测试集B相同，其功能为分析过拟合程度。网络训练过程中将会对比测试集B与对照集C的预测结果从而监视过拟合情况。

2.2 算法流程图

BP神经网络的算法流程如图3所示。

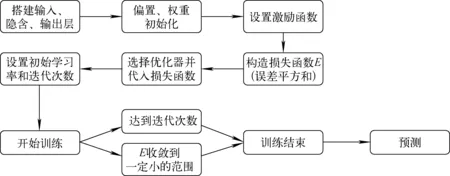
图3 BP神经网络算法流程图Fig.3 Algorithm flow chart of BP neural network

整个网络的搭建基于python上的开源框架tensorflow。

1) 权重、偏置的初始化与激励函数选取

由式(6)，初始权重的值如果相同，初始输入差别就会很小，为加速收敛，使用tensorflow内置的truncated_normal函数，产生[-2,2]范围中服从标准正态分布的随机值作为权重的初始值。

神经网络的偏置一般设置为0.1～1[15]，结合国外关于压水堆的神经网络研究[11]和数值实验，设置偏置为b=0.1。

由于本次实验的输入向量归一化后处于区间[-1,1]，所以选择映射到[-1,1]之间并且具有对称性的tanh函数作为激励函数。

2) 梯度下降算法的改进与自适应学习率优化器的选取

自适应学习率相对于固定学习率优势明显，其能根据损失函数的变化合理调整大小，加速搜索速度。tensorflow中优化器集成了梯度下降算法与权重更新的功能，通过实验比较，在众多优化算法中选择损失函数最小且下降最快的AdamOptimizer算法。

AdamOptimizer是常规梯度下降算法的改进算法。AdamOptimizer的权重更新方式如下：

(7)

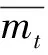
mt=β1mt-1+(1-β1)gt

(8)

(9)

(10)

(11)

(12)

(13)

式中：β1、β2为衰减速率，一般设置β1=0.9,β2=0.999；gt为梯度；lr0为初始学习率，实验设置lr0=0.03。当mt与vt被初始化为0向量，则它们就会向0偏置，所以做了偏差校正，即式(10)、(11)，从数学上来讲，mt、vt实际就是梯度的一阶、二阶矩估计。

AdamOptimizer相较于传统学习率固定的梯度算法，通过式(12)令学习率自适应变化，同时优化了梯度下降算法，令整体收敛效率相对传统算法得到提升，并且提高网络的预测精确性。

3) 隐含层神经元节点数的选取

隐含层节点数的选择对于神经网络的优化至关重要，隐含层节点数会直接影响网络的性能。一个基本原则是，应选择合理的隐含层节点数，使网络的整体自由度与数据样本数相当。选用AdamOptimizer，迭代8 000次，测试神经元数在70～400范围内的误差变化。每间隔10个神经元统计1次测试集30组数据样本的平均相对误差与最大相对误差，如图4所示。

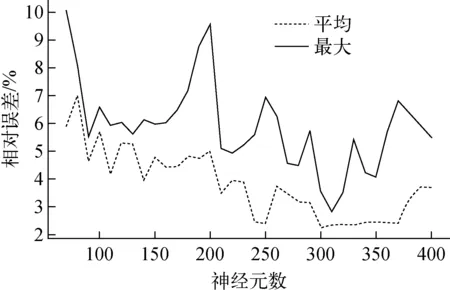
图4 神经元数-误差曲线Fig.4 Curve of neuron number and error

从图4可得，神经元数在[300,350]范围内有较好的预测精度，根据网络结构尽量紧凑的原则，选取神经元节点数为300。

4) dropout方法动态调整节点数

当模型复杂而训练样本数量不足时，网络会在学习全局特征的同时也将局部特征或噪声特性一起学习，出现过拟合，导致网络失真、预测精度下降。在迭代次数8 000次的实验条件下，每50次记录对照集和测试集30组数据的平均相对误差，分析过拟合情况，绘制成图5。

从图5可发现，迭代次数大于1 000次后，对照集与测试集的平均相对误差出现了明显的差距，两个数据集之间结果的差距接近2%，出现过拟合现象。采用dropout方法降低过拟合危害。对于BP神经网络，dropout方法在每次迭代优化器更新权重后，随机将一部分神经元节点对应权重重置为0，实际达到了动态神经元节点的效果。dropout方法的优势可总结为以下3点：1) 每次迭代时各神经元节点均与不同的神经元一起训练，削弱了各神经元之间的耦合性，增强了网络的泛化；2) 增强了数据的特征提高了网络的稀疏度；3) 每个神经元没有百分百参与学习，使得节点不会过度学习。实验中设置dropout重置权重比率为20%，在其他条件与图5实验条件一致的情况下，重新进行实验，绘制曲线示于图6。

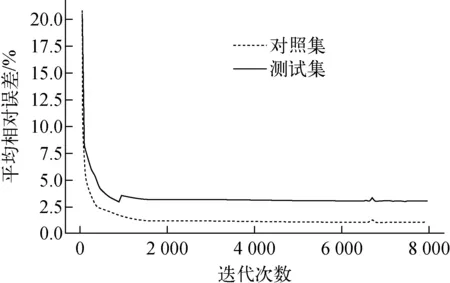
图5 过拟合下测试集、对照集误差对比Fig.5 Error comparison of test set and contrast set under overflow

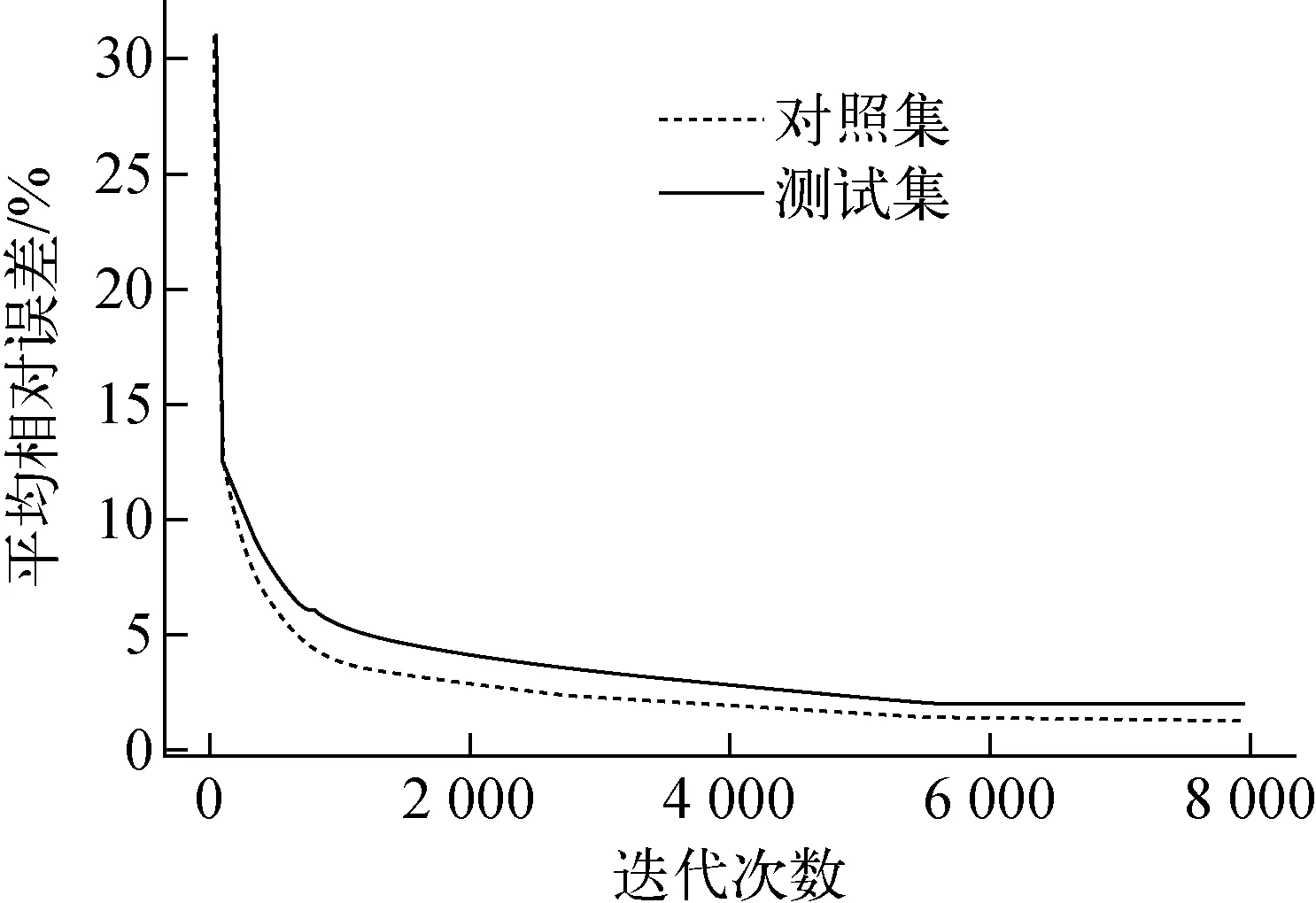
图6 dropout修正后测试集、对照集误差对比Fig.6 Error comparison of test set and contrast set after dropout modification

由图6可明显看到对照集与测试集的平均相对误差曲线相对于图5有了很大的接近。测试集与对照集的差距在1%左右，相对于不使用dropout的方法差距缩小了60%以上，说明dropout方法有效地改善了过拟合现象。

3 实验结果

对3个参数的预测情况进行了数值实验，结果列于表1。实验条件设置为迭代次数为8 000次，初始学习率为0.03，神经元节点数为300。独立重复进行10次实验，统计测试集30组数据样本的预测结果与原始数据对比后的最小相对误差、最大相对误差、平均相对误差(MRE)、均方误差(MSE)，以及相对误差小于1%的样本数与相对误差大于5%的样本数。MSE与MRE由下式给出：

(14)

(15)

式中：fi为预测值；yi为实际值；n为样本数量。MSE与MRE越小，预测效果越好。

从表1发现，每个参数的平均相对误差均小于2%，均方误差均小于0.003，最大相对误差在5%附近，说明预测误差小、精度较高。图7统计了3个参数的误差分布情况，84%的数据相对误差均在2%以下，说明预测可靠性较高。

表1 误差分析Table 1 Error analysis

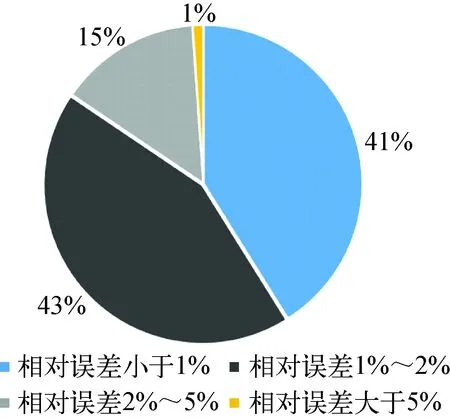
图7 误差分布饼图Fig.7 Pie chart of error distribution

4 结论

本文运用新型人工智能方法——BP神经网络方法，通过自适应调整网络结构和参数，相对于传统方法，快速准确地预测了秦山二期压水堆堆芯燃料换料3个关键参数，其结果可推广至任意堆芯堆型、任意关键参数预测。该方法不需特定领域的专业知识，只要有足够多的数据，即可实现精度较高的快速预测，有很好的应用前景。在核工业领域，对于神经网络方法的理论研究和应用拓展，还需进一步进行研究。