功果桥大坝坝顶水平位移安全监控指标拟定
2020-03-30汪俊波俞年年
汪俊波,李 黎,程 帅,俞年年
(1.西安热工研究院有限公司,陕西 西安 710054;2.华能澜沧江水电股份有限公司,云南 昆明 650206)
大坝安全监控指标是对在役大坝的效应量所规定的正常状态与非正常状态的界限值。对大坝运行期的监测数据进行指标拟定,合理确定监控指标或预警值,对于大坝运行管理以及状态评估具有重要的指导意义。
在拟定大坝安全监控指标的众多方法中,置信区间估计法、典型小概率法较为常用[1],在监测资料丰富可靠的情况下,该两种方法可取得合理的计算结果[2-4]。查阅相关的文献,采用典型小概率方法拟定监控指标主要是以正态分布方法居多[4-6],对数正态分布和极值Ⅰ型分布的检验方法和计算案例较少。本文对典型小概率方法几种常用分布检验步骤、计算方法进行了归纳和梳理。与此同时,以功果桥大坝为工程依托,选取大坝3号、5 号、8号、10号等四个典型坝段的水平位移测点作为监控点,结合历史观测数据,通过典型小概率法和统计模型的置信区间法分别计算了相应坝段的位移监控指标,并对两种方法计算的结果与历史极值进行比较分析,进而对监控指标进行综合拟定,为电厂运行管理和状态评估提供依据。
1 工程概况
功果桥水电站位于云南省云龙县大栗树西侧,电站以发电为主,水库正常蓄水位1 307 m,相应库容3.16亿m3。拦河大坝为碾压混凝土重力坝,最大坝高105.0 m,坝顶总长361.0 m。坝顶布设16个引张线测点用以监测坝顶的水平位移。工程于2007年10月开工,2011年9月底大坝下闸蓄水,2012年3月工程竣工。
2 指标拟定方法
2.1 典型小概率法
选择不利荷载组合时的监测效应量xmi,得到一组样本:
x={xm1,xm2,…,xmn}
(1)
由已知随机变量x的n个观测值,其统计量样本均值μ、标准差σ、变异系数δ可用下列公式估计其统计特征值:
(2)
(3)
(4)
然后,用统计检验方法,对其进行分布检验,确定分布函数F(x)和概率密度函数f(x)。
令xm为效应量的极值,若当x>xm时,大坝将要出现异常或险情,其概率为:

(5)
求出xm的分布后,估算xm的问题转换为确定大坝出现异常概率α,其值根据大坝的级别和重要性而定[7-11],通常取α=5%,由xm的分布函数直接求出xm=F-1(x,σx,α)。
在工程结构可靠度分析中,对于子样较少的分布检验,通常采用K-S检验法,K-S法的步骤为[12-14]:
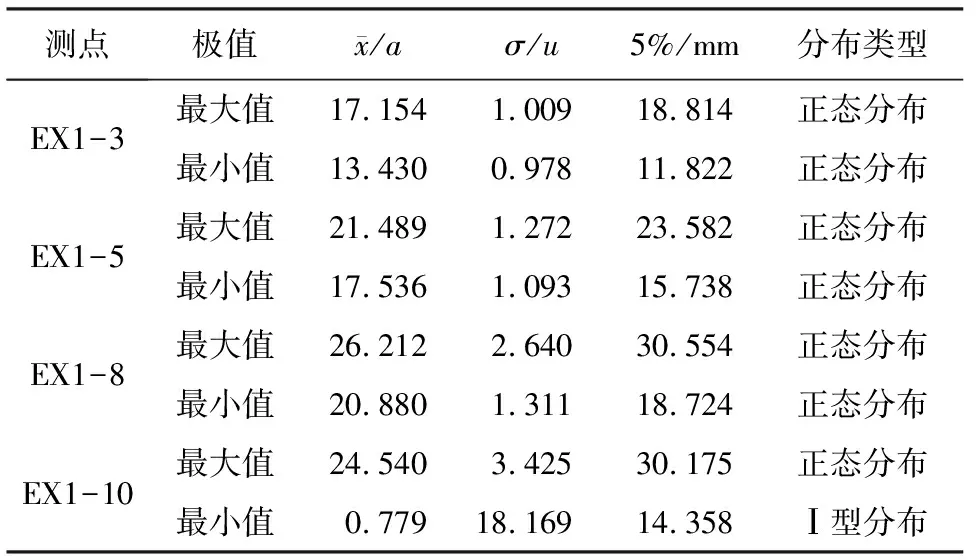
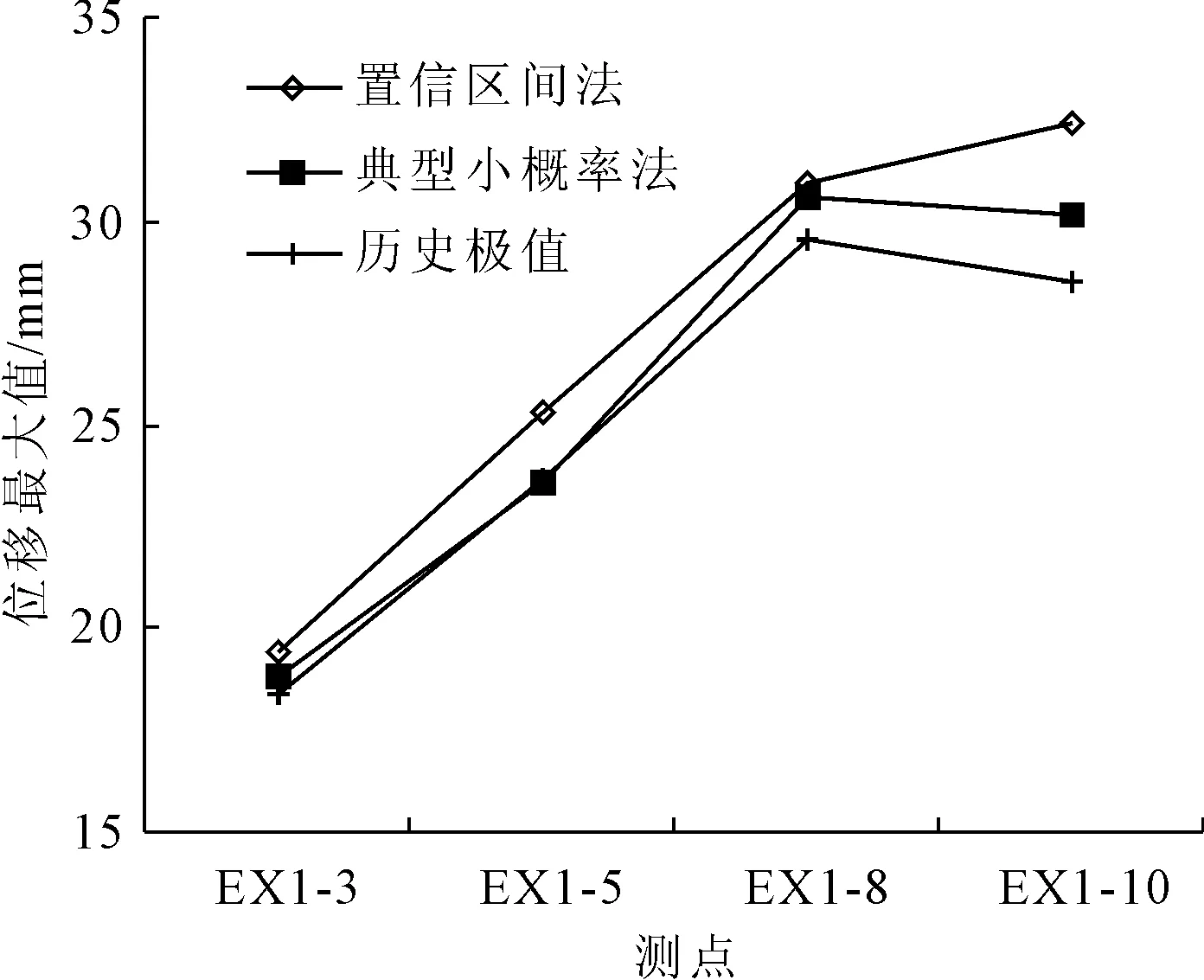
(1) 将各监测量数值排序(x1 (6) (2) 按式(7)—式(9)分别编程计算假设正态分布,对数正态分布、极值Ⅰ型分布函数的理论分布F(xk): (7) 其中μ和σ按式(2)、式(3)计算。 (8) F(xk)=exp[-exp(-a(x-u))] (9) 式中a=1.2855/σ,u=μ-0.57722/α;其中μ和σ按式(2)、式(3)计算。 (3) 用子样的经验分布Fn(xk)和假设的理论分布F(xk)建立统计量: Dn=max1≤k≤n{ |Fn(xk)-F(xk)|,|Fn(xk-1)-F(xk)|} (10) (4) 根据显著性水平(取0.05),查K-S检验临界值表[15],得到Dn,0.05,若Dn 根据成熟的理论模型,结合功果桥大坝的特点,其位移主要受水压、温度以及时效等因素的影响,考虑初始值的影响,其大坝位移的统计模型为: (11) 根据式(11)和去除粗差后的历史观测数据,可计算出监测效应量和原因量的数学模型,当计算精度较高时(一般要求复相关系数大于0.85),则可用该数学模型计算监控指标: (12) 取显著水平α=5%,则β=1.96。由式(12)可计算出相应测点监测量的上下限值,如果实测值在区间内且无明显性趋势变化,可认为运行正常,反之是异常的。 混凝土坝体的表面变形主要受上游水深和温度影响,一般在冬季,即上游水深较大、气温较低时,坝顶位移会出现向下游方向的较大值,反之,在夏季低水位时会出现向下游方向的较小值。因此,选取每年的位移最大、最小值作为典型效应量的样本,极值统计见表1[16]。 表1 功果桥大坝典型坝段水平位移极值统计 下面以EX1-10为例进行计算说明: F(δ>δm1)= (13) 由式(13)可计算出δm1(5%的概率)的最大极值为30.175 mm。 经过K-S检验,引张线EX1-10的最小值满足极值Ⅰ型分布,即δ-F(α2,μ2),其特征值α2=0.779,μ2=18.169,则δ<δm2(位移的极值)时,其概率为: (14) 由式(14)可计算出δm2(5%的概率)的最小极值为14.358 mm。 其他测点的计算结果见表2。 表2 典型小概率法计算结果 结合水位、温度、时间历时资料,计算出上游水位对应5%概率的水位限值。在最大值计算时,选取上游水深的上限值,计算最小值时选取上游水深的下限值。引张线监控指标置信区间法计算结果见表3。由计算结果可知,统计模型的复相关系数都在0.92以上,计算精度较高,与实测值拟合程度较好,该方法计算结果可作为综合拟定时的依据。 以引张线EX1-3为例,统计模型的标准差S=1.118 mm,则置信区间Δ=±1.96S=±2.191 mm。该点的监控指标可用下式估计: δm=δ±2.191=7.66+0.00×(H-H0)+ 0.344×(lnθ-lnθ0)±2.191 (15) 根据引张线EX1-3的测点水位和时间历史资料,根据式(11)和式(12)可求出水平位移的下限值10.731 mm,上限值19.422 mm。如果测值在该区间内且无明显性趋势变化,则认为测值正常,反之,则认为测值异常,应加强观测和分析,查找原因,必要时采取相应的措施。 表3 置信区间法计算结果 变形项目监控指标主要从典型小概率法、置信区间估计法、时段极值三个方面进行综合拟定,在满足三种方法适用条件的前提下,原则上选择上述数值中的最大或最小值,设计计算值作为参考[17]。具体拟定结果见表4和图1、图2。 表4 引张线监控指标综合拟定结果 典型小概率法计算结果和历史极值数据最为接近和吻合,置信区间法计算的最大最小值范围相对较宽,表明大坝有继续抵御更大荷载下的变形余量。在两种计算结果都小于设计值的情况下,综合拟定,主要以置信区间法的计算结果为准。 测点EX1-8位于最大河床部位坝段,从统计的历史极值和典型小概率法计算结果来看,该测点向下游方向的位移比其他测点大,符合工程实际情况。但置信区间法的计算结果,EX1-10的位移最大值明显大于EX1-8的位移最大值,与实际不符,故EX1-10的位移最大值综合拟定采用典型小概率法计算结果。 图1 三种方法确定的位移最大值分布图 图2 三种方法确定的位移最小值分布图 (1) 通过统计模型的置信区间法和典型小概率法可计算大坝典型坝段的位移监控指标,并结合设计值、历史极值对监控指标进行综合拟定,为电厂运行管理和状态评估提供依据。 (2) 典型小概率法计算结果和监测历史数据最为接近和吻合,置信区间法计算的最大最小值范围相对较宽,表明大坝有继续抵御更大荷载下的变形余量。可结合设计值对其监控指标进行综合拟定。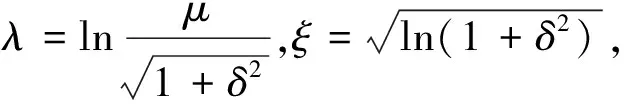
2.2 置信区间法
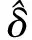
3 拟定结果
3.1 典型小概率法




3.2 置信区间法

3.3 指标的综合拟定


4 结 论
