考虑隧道开挖时间影响的一种支护结构计算方法
2020-03-30白浪峰曹校勇
白浪峰,曹校勇,徐 平
(中交第一公路勘察设计研究院有限公司,陕西 西安 710075)
从十二五计划开始,我国设计行业获得了一个全新的发展契机,由于勘察设计企业众多,加之投资者对工程管理的信息一体化,为了能在诸多勘察设计企业中保持一定的优势,实施精细化设计是一种科学有效的措施。
近年来,数值分析已成为大型地下工程设计的一种重要手段,其关键是选择合适的土体本构模型和计算参数。隧道工程岩土体应力路径复杂,岩土体开挖属于卸载,研究表明[1-4]卸载模量是加载模量的2倍~4倍,这在隧道工程数值分析中应引起充分注意。目前用于岩土工程分析的土体本构模型主要有:邓肯-张(DC)模型、莫尔-库仑(MC)模型、修正剑桥(MCC)模型、硬化土(Hardening Soil,HS)模型及小应变硬化土(Hardening Soil Model with Small-strain,HSS)模型等[5-6]。DC模型为非线性弹性模型,可以反映土体应力、应变的非线性特性,但却不能反映土体的塑性应变,也不能反映隧道工程不同的应力路径;MC模型会过高估计隧道仰拱或底板的隆起量;MCC模型和HSS模型模型参数较多且较难确定[7-8]。HS模型适合软土及较硬岩土体的破坏和变形行为的描述[9],其主应力空间的屈服面并不是不变的,而是随着塑性应变而扩张。HS模型的岩土体刚度模量是与其应力水平相关的,不仅可以反映岩土体应力、应变的非线性特性,而且模型参数简单,可以从常规三轴试验和固结实验获得。
隧道初期支护结构精细化设计的关键点在于围岩应力释放系数的确定。Carranza等[10]用经典的收敛-约束法探讨了隧道纵面变形曲线(LDP)和土体反力曲线(GRC)的关系,Vlachopoulos等[11]考虑了围岩塑性区半径对变形的影响,提出了一种改进的隧道纵面变形曲线计算方法。本文基于前人的工作,提出关于应力释放系数和隧道径向变形的土体反力曲线,从而建立了应力释放系数与隧道掘进尺度的关系,精确定义隧道每一施工步的围岩应力释放系数。
1 数值分析的理论基础
1.1 HS本构模型介绍
土体硬化模型是以经典塑性理论为基础的屈服面模型。它的弹性部分采用了合理的双刚度,加卸载模量分别定义,考虑了岩土体压硬性[12-13]。塑性部分采用非关联流动法则和各向同性的硬化准则,较好地描述了岩土体的双曲线形式的应力-应变关系,如图1所示。其中qa为抗剪强度的渐进值,qf为极限偏应力,qa与qf之间的比值由破坏比Rf给出,Rf=qf/qa。
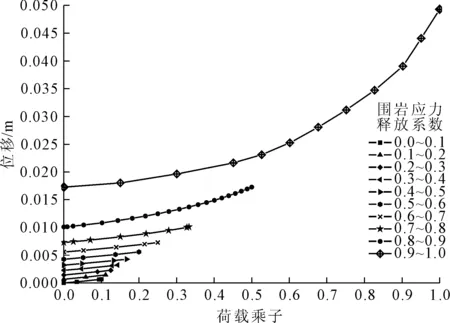
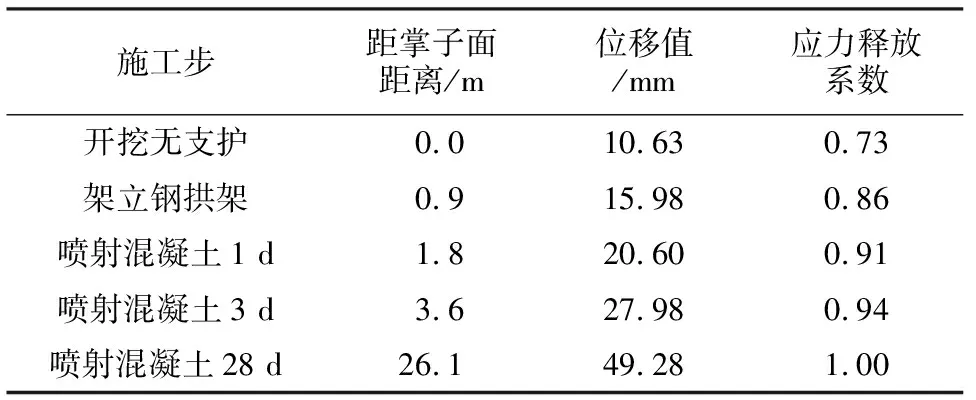
当q (1) 式中:E50是主加载下与围压有关的刚度模量,它由下面方程式给出: (2) 当q≥qf时,岩土体处于塑性阶段,产生塑性变形,随着硬化参数的变化,岩土体同时发生剪切硬化和压缩硬化。 图1 标准排水三轴试验的应力-应变关系 为了确定隧道初期支护的合理支护时机或者优化初支在隧道特定变形下的支护能力,研究隧道的纵面变形曲线是很有必要的。在隧道掌子面前方的围岩已经发生了一部分径向变形,随着掌子面掘进,径向位移逐渐增大,而且距掌子面后方足够远的隧道轮廓的径向变形将趋于收敛,这种把掌子面掘进距离和隧道径向变形关联起来的曲线称之为纵面变形曲线(LDP)。Vlachopoulos等[11]通过三维数值分析,考虑原岩应力、岩体质量、开挖步距、塑性区等因素,基于Panet[14]提出的解析解公式,拟合出改进的LDP曲线公式。 沿隧道轴向,掌子面前后断面的径向位移为: (3) 式中:x*=x/Rt,x为隧道断面距掌子面的距离,x小于0表示断面在岩体内部,反之则在已开挖隧道内。 (4) 式中:R*=Rp/Rt,Rp为塑性区半径,Rt为隧道半径,u0为掌子面处的隧道径向位移,umax为隧道径向位移的最大收敛值。 经典的土体反力曲线(GRC)可由解析解导出,描述的是隧道内部压力pi与隧道径向变形之间的关系,这种关系与岩土体的物理性质密切相关。隧道内部压力pi是一个假想的力,模拟的是隧道内开挖岩土体在隧道轮廓线上的径向反力,这个力在初始开挖前等于原岩应力p0,随着隧道开挖逐渐释放直至为零。LDP与GRC之间的关系如图2所示。SCC曲线为支护特征曲线。 本文建立数值分析模型,以隧道拱顶中心点为监控点,得出围岩应力释放系数与拱顶沉降相关的GRC曲线。假定支护结构承担的压力为(1-β)p0,则隧道开挖后围岩应力释放了βp0,β称之为应力释放系数。运用数值模拟来推导GRC曲线有传统方法不能比拟的优势,数值模拟方法能够考虑围岩水平侧应力系数对隧道径向位移的影响。结合LDP曲线,从而把掌子面掘进距离和围岩应力释放系数联合起来,便于隧道工程结构设计的实际应用。以断面距掌子面距离a为例,ab虚线与LDP曲线交于b点,确定此时对应的径向位移,然后过b点做垂直于x轴的直线bc并与GRC曲线交于c点,过c点做平行于x轴的直线cd并与y轴交于d点,由此可以确定特定断面处对应的围岩应力释放系数。如图3所示。 图2 LDP曲线与GRC曲线之间关系 图3 改进的LDP曲线与GRC曲线之间的关系 隧道的初期支护结构主要有喷射混凝土、锚杆以及型钢或格栅。其中,喷射混凝土和型钢/格栅组合使用,可以看作组合梁结构。组合梁的弹性模量和厚度由混凝土和钢材的刚度决定。由于软弱围岩在隧道开挖时破碎膨胀,塑性区也比较大,锚杆的作用受限,因此本文不考虑锚杆的受力,锚杆仅作为支护体系的安全储备,这样结果是偏于保守的。 二维平面应变模型里喷射混凝土、型钢/格栅的轴向刚度和抗弯刚度可按下式计算: 对喷射混凝土: (5) 对钢材: (6) 式中:E是弹性模量;A是截面积;I是惯性矩;v是泊松比。 组合梁的等效轴向刚度和等效抗弯刚度可由下式表示: Deq=n(Dr+Ds) (7) 式中:n=1/b,b为型钢/格栅沿隧道纵向的间距。 求得组合梁内力后,喷射混凝土和钢材各自承担的内力可按刚度分配: (8) 式中:下标i代表喷射混凝土或者钢材。 求得每种结构承担的内力后,就可以对结构进行安全性评价。由于喷射混凝土物理性质的复杂性,为了消除地下工程不可预知的因素和未知荷载,本文采用一种简便方法,仅使用构材的极限单轴抗压和抗拉强度[15],并采用全局安全系数Fs,来分析构材的承载能力。 (1)N-M承载能力。最大的拉压应力由下式导出: (9) 当M=0时可求得最大和最小轴力: (10) 当最大的拉压应力同时发生时M最大: (11) (2)N-Q承载能力。矩形梁截面的最大和最小主应力由下式表示: (12) 当最大最小主应力同时发生时Q最大: (13) 把式(13)带入式(12)可求得: (14) 以某隧道工程为例,复理石发育,围岩软弱破碎,埋深较深,采用五级围岩支护。支护参数为:C30喷射混凝土28 cm;型钢I20b,纵向间距60 cm;双层Φ8钢筋网20 cm×20 cm。 为了保证本工程施工质量,实验室做了大量关于喷射混凝土强度的试验。试验参数见表1、表2。 表1 喷射混凝土力学性能指标 表2 型钢材料指标 根据表1、表2的材料参数,结合式(5)—式(7),可以算出由钢拱架和喷射混凝土组合成的复合梁的等效刚度,如表3所示。 表3 复合梁刚度 数值分析模型及地质参数如图4所示。 (1) 确定GRC曲线和LDP曲线。为了确定GRC曲线,运用有限元数值方法研究围岩应力释放系数与拱顶沉降的关系。设定围岩应力释放系数β从0.0~1.0按0.1的等差数列增长,共有10个计算步,随着围岩应力释放,隧道轮廓位移逐渐向隧道内方向收敛,进而获得与特定释放系数对应的拱顶沉降值。图5的横坐标荷载乘子表示计算过程,当荷载乘子等于1.0时表示计算完成。图5的每条曲线表示特定应力释放系数区间内的拱顶沉降值变化情况。由计算可得拱顶最大位移值umax=49.28 mm,R*=Rp/Rt=2.9。 图4 数值模型草图(单位:m) 图5 拱顶位移与释放系数的关系曲线 把umax和R*代入式(3)—式(4),可以得出本隧道对应的LDP曲线,如图6所示。 图6 拱顶位移与掘进尺度的关系 (2) 确定围岩应力释放系数。五级围岩段设计掘进尺度0.6 m,平均每天1.5个循环。根据掘进速度可求得特定施工步距掌子面的距离,根据图6可求得与掌子面距离对应的拱顶沉降,然后根据图5曲线,由拱顶沉降值反求应力释放系数。当沉降值为图5中数据的中间值时,释放系数可按内插法确定。详细结果如表4所示。由表4可知,隧道开挖后围岩应力释放系数为0.73,安装钢拱架后应力释放系数为0.86,实际操作时,本计算步的释放系数增量为0.13。后续施工步的释放系数以此类推。 表4 施工步与释放系数的关系 根据1.3节的计算方法,可以绘制出钢拱架和喷射混凝土对应的M-N、Q-N包络图。通常有限元模型的网格节点较多,利用传统方法逐个断面进行安全判断较为麻烦,结合内力包络图,直接与衬砌每个节点的内力进行对比,能够方便快速的判定初支结构是否安全。本文采用的安全系数Fs=1.60。M-N、Q-N包络图见图7、图8。 图7 钢拱架内力与包络图 图8 喷射混凝土内力与包络图 从图7、图8可以一目了然的看出设计的支护参数是在每个施工阶段都是安全有效的。可以发现,钢拱架暂时独立承担围岩荷载时受力最大,随着喷射混凝土的施作和硬化,喷射混凝土承担了越来越多的围岩荷载,喷射混凝土成为承担围岩荷载的主要支护结构。 隧道开挖是一个四维问题,时空效应一直是隧道工程学术研究的一个难点。本文结合经验公式和数值模拟,有效的把时间因素和空间因素联系起来,运用二维平面应变模型简捷快速的计算隧道初期支护结构的安全性,得出以下结论: (1) 硬化土(HS)本构模型比经典的摩尔-库仑(MC)模型更适宜模拟隧道开挖。 (2) 隧道工程支护参数的确定,不仅要保证施工完成后的安全性,而且要满足各施工阶段的安全。 (3) 用内力包络图可以快速评判支护结构的安全性,极大的提高了工作效率。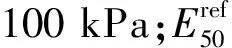
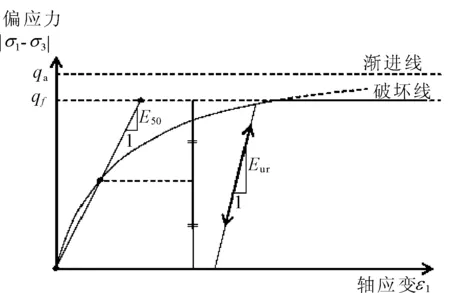
1.2 改进的LDP与GRC之间的关系

1.3 初期支护结构的安全评价方法
Keq=n(Kr+Ks)
2 工程分析实例
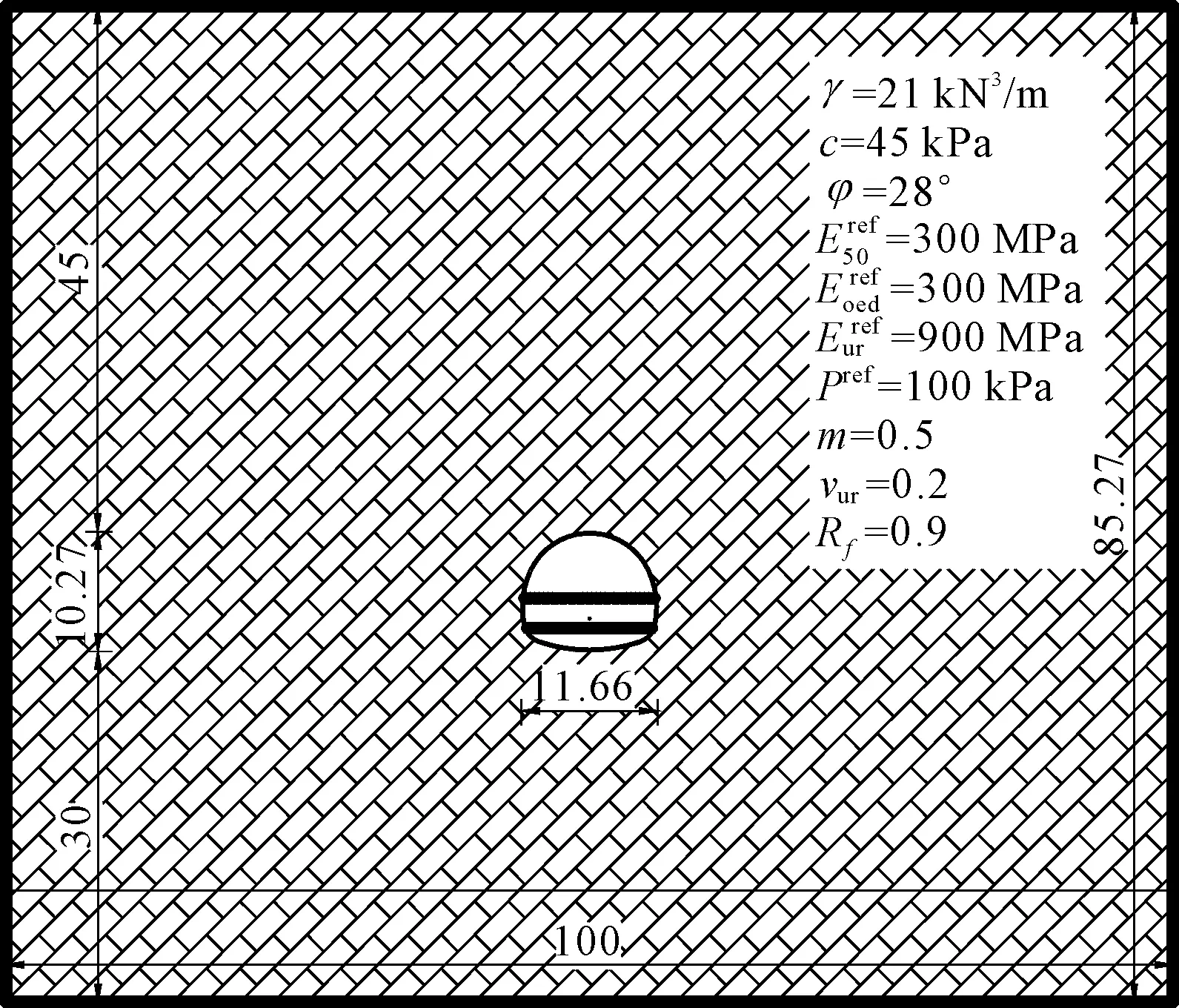
2.1 数值模型的建立



2.2 应力释放系数的确定

2.3 结果分析


3 结 论
