采用底部开缝立方体劈拉试件测定混凝土起裂断裂韧度
2020-03-30于菊瑶
于菊瑶,董 伟
(大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024)
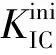
目前实验室测定起裂断裂韧度的常用方法有三点弯曲梁试验方法和楔入劈拉试验方法,由于三点弯曲梁受力形式明确,且试验操作简单,对试验机刚度要求不高,已被国际材料结构与研究实验联合会(RILEM)[8]推荐为断裂韧度测定的标准方法。但由于试件跨高比较大且自重影响不能忽略,搬运过程中可能会给预制裂缝尖端造成不可恢复的损伤从而影响测量结果的准确性[9]。相比于三点弯曲梁法,楔入劈拉法的主要优点体现在消除了试件自重对断裂参数计算结果的影响。2005年,楔入劈拉法被我国《水工混凝土断裂试验规程》[10](DL/T 5332—2005)推荐为混凝土断裂韧度测定的标准方法。但由于试验加载装置较为复杂且刚度对结果有一定影响,增加了试验操作的难度[11]。
除了上述两种常见的断裂试验方法之外,Ince[12-13]于2010年首次采用中央带缺口的立方体劈拉试件测定双参数断裂模型[14]的断裂参数,通过与三点弯曲梁以及圆柱体劈拉试件的试验结果对比,证明了该方法的有效性。在此之后,Pandey等[15]采用中央带缺口的立方体劈拉试件与紧凑劈拉试件开展了双K断裂参数的试验研究,结果表明两种试验方法得到的双K断裂参数与黏聚韧度吻合良好,验证了中央带缺口立方体试件同样适用于双K断裂参数的测量。在此基础上,Hu等[16]采用中央带缺口立方体试件研究了加载速率对双K断裂参数的影响。 相比于其他形式的试件, 中央带缺口的立方体劈拉试件主要优点在于试件轻便且试验加载装置简单,避免了自重对断裂参数计算的影响。但是中央贯通裂缝无法通过后切割制备,需要提前在试件预设钢片,在钢片抽离过程中易对缝尖造成损伤,进而影响测量结果。
基于以上分析,本文提出了一种底部开缝立方体劈拉试件测定混凝土起裂断裂韧度的试验方法。首先测量高度为100 mm、200 mm和300 mm,缝高比为0.2、0.3、0.5和0.7的立方体劈拉试件及三点弯曲梁的起裂荷载,进而结合拟合立方体劈拉试件缝尖的应力强度因子计算公式,计算其起裂断裂韧度。通过对比三点弯曲梁的测试结果,验证了该方法的有效性。
1 试验概况
1.1 试件准备
本试验采用底部开缝立方体(见图1)和三点弯曲梁(见图2)两种试件形式,按照试件高度不同分为A、B、C三个系列,对应的试件高度D分别为100 mm、200 mm和300 mm,三点弯曲梁跨高比S/D=4,宽度B=100 mm。A系列设置了四种不同初始缝高比a0/D,分别是0.2、0.3、0.5和0.7,每组工况制作3个试件,共计36个试件。混凝土配合比为:水泥∶砂子∶石子∶水=1.0∶2.0∶3.7∶0.6。其中水泥采用大连小野田水泥有限公司生产的P.O42.5普通硅酸盐水泥,粗骨料最大粒径为10 mm,所有试件养护80 d后切缝进行试验。参照《普通混凝土力学性能试验方法标准》[17](GB/T 50081—2002),采用300 t电液伺服压力试验机测定混凝土基本力学性能参数。其中劈裂抗拉强度试验和立方体抗压强度试验采用尺寸为150 mm×150 mm×150 mm的立方体试件,静力受压弹性模量试验采用150 mm×150 mm×300 mm的棱柱体试件。试验测定材料的各项力学参数为弹性模量E=33.1 GPa,抗拉强度ft=3.31 MPa,立方体抗压强度fcu=45.1 MPa。
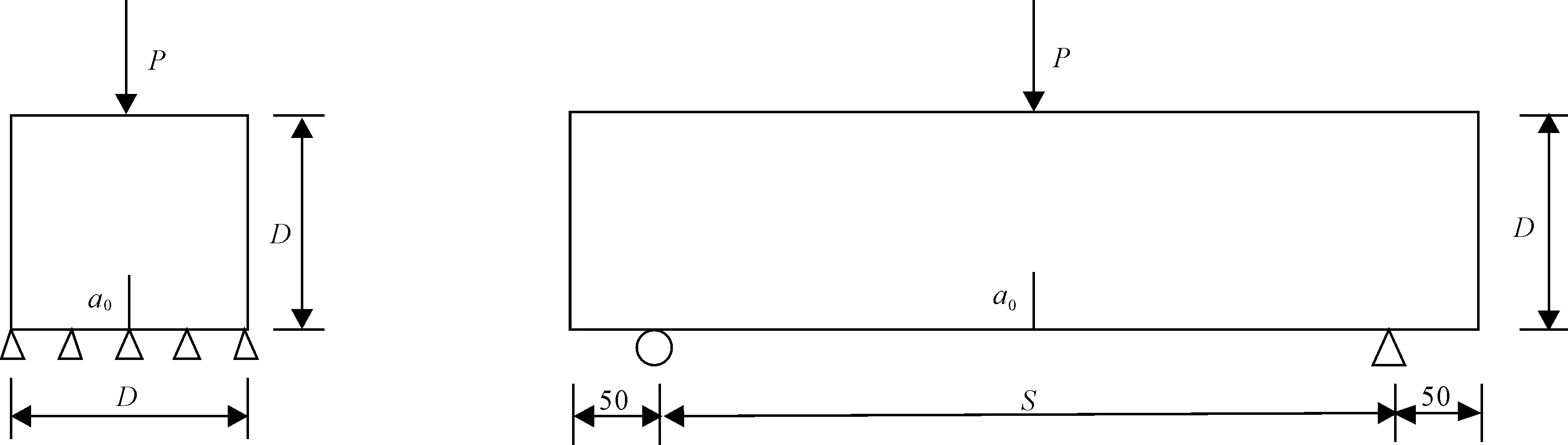
图1底部开缝立方体劈拉试件示意图图2三点弯曲梁试件示意图
1.2 底部开缝立方体劈拉试验
立方体劈拉试验在300 t电液伺服压力试验机上进行,通过IMC数据采集系统采集数据。为了消除立方体劈拉试件与试验机底板的摩擦,将减摩片固定在试验机底板中央,并在其上表面均匀涂抹润滑油后再放置混凝土试件于减摩片上。在预制裂缝尖端左右各10 mm处对称粘贴应变片,监测裂缝尖端的应变变化,从而确定起裂荷载。在预制裂缝中间高度处布置夹式引伸仪测量该位置处的张开位移。本次试验采用位移控制模式,加载速率为0.06 mm/min。
1.3 三点弯曲梁试验
三点弯曲梁试验在25 t电液伺服万能材料试验机(MTS)进行,通过IMC数据采集系统采集数据。应变片布置方式同底部开缝立方体劈拉试件,且在梁加载点处和裂缝张开位置布置夹式引伸仪测量加载点位移δ和裂缝张开口位移w[18]。同样采用加载速率为0.06 mm/min的位移控制模式。
2 试验结果分析
2.1 应力强度因子计算
采用ANSYS有限元软件中提供的位移外推法[19]计算不同试件高度、不同缝高比以及在外荷载作用下的缝尖应力强度因子,进而通过其形状函数拟合得到底部开缝立方体劈拉试件的应力强度因子公式。为了模拟裂缝尖端各点应力的奇异性,把裂缝尖端周围的等参单元各条边中的节点移至靠裂缝尖端的1/4分点处[20]。通过调整试件的缝高比及试件尺寸(缝高比为0.05~0.95,间隔0.01,试件边长为50 mm~2000 mm,间隔50 mm),拟合得到适用于底部开缝立方体劈拉试件的应力强度因子表达式,如式(1)所示:
12.64(a/D)2-12.65(a/D)3+11.51(a/D)4]
(1)
式中:P为外部荷载, kN;D为立方体劈拉试件边长, mm;a为裂缝长度, mm;K为应力强度因子,MPa·mm1/2。
图3为底部开缝立方体劈拉试件在不同加载条件下其应力强度因子随缝高比变化的拟合曲线,拟合结果与计算点吻合良好。
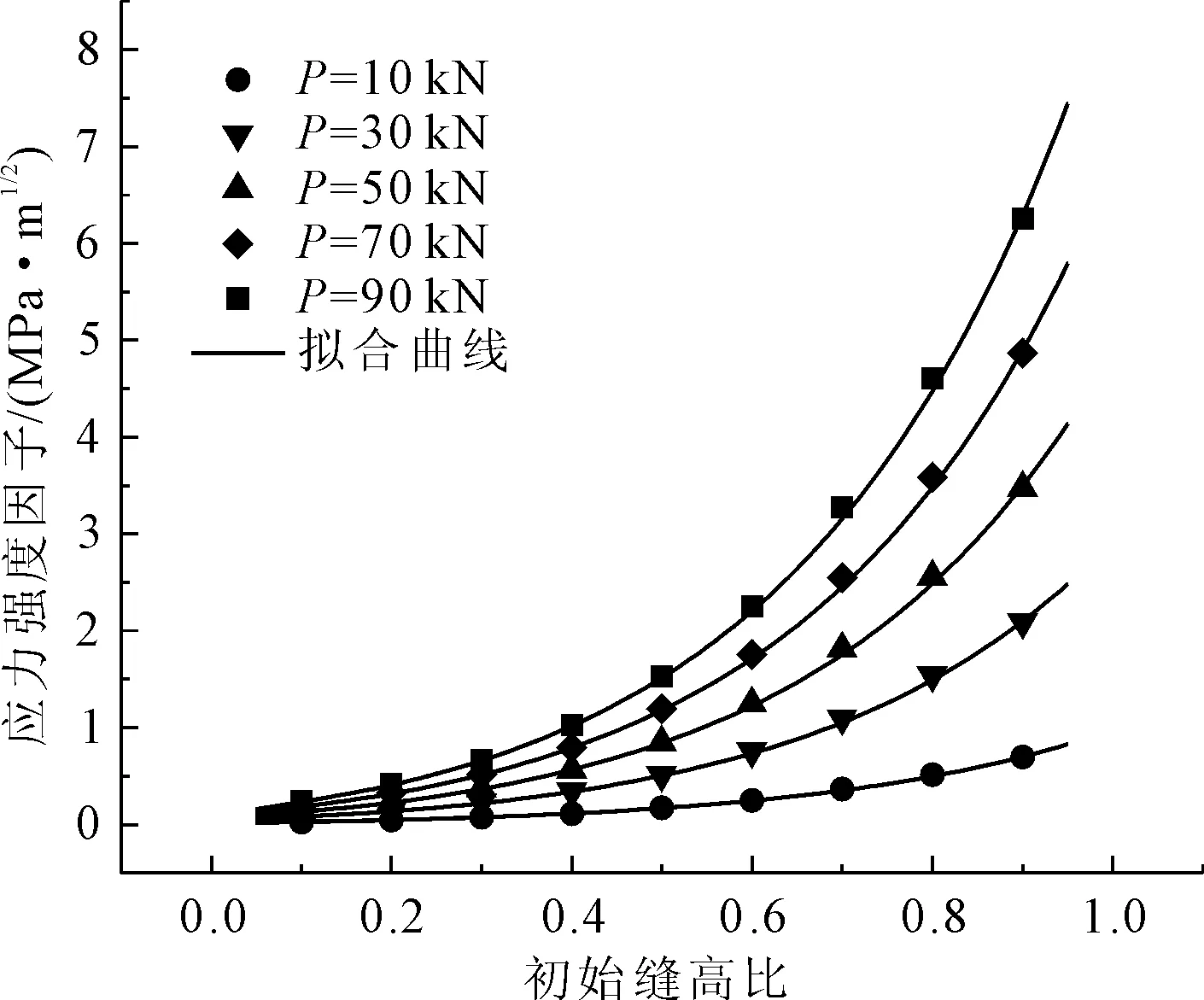
图3 不同荷载条件下应力强度因子拟合曲线
2.2 起裂荷载与起裂韧度的确定
本文采用电阻应变片法确定试件的起裂荷载[21]。由于起裂后裂缝尖端两侧混凝土弹性应变能释放,裂缝尖端左右两端对称粘贴的应变片数值出现回滞,回滞点对应的荷载为起裂荷载,如图4所示。其中Pini为试件的起裂荷载,εmax为最大应变值。
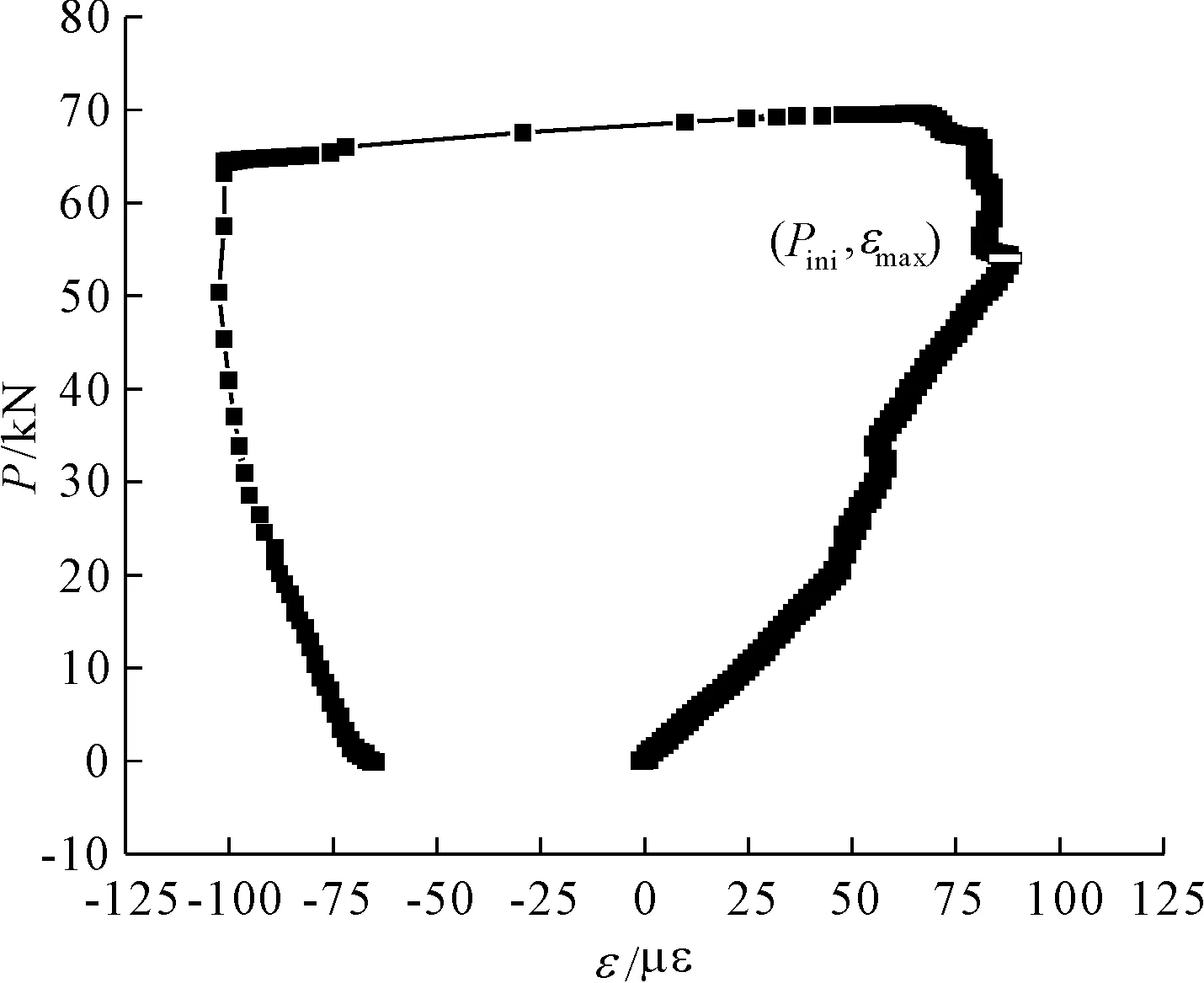
图4 底部开缝立方体劈拉试件起裂荷载确定
三点弯曲梁缝尖的应力强度因子采用RILEM推荐的公式(2)和公式(3)进行计算。将Pini、a0、D分别带入式(1)和式(2)、式(3),即可得到三点弯曲梁试件与底部开缝立方体劈拉试件的起裂断裂韧度,计算结果列于表1和表2。
(2)
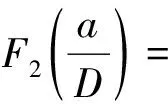
(3)
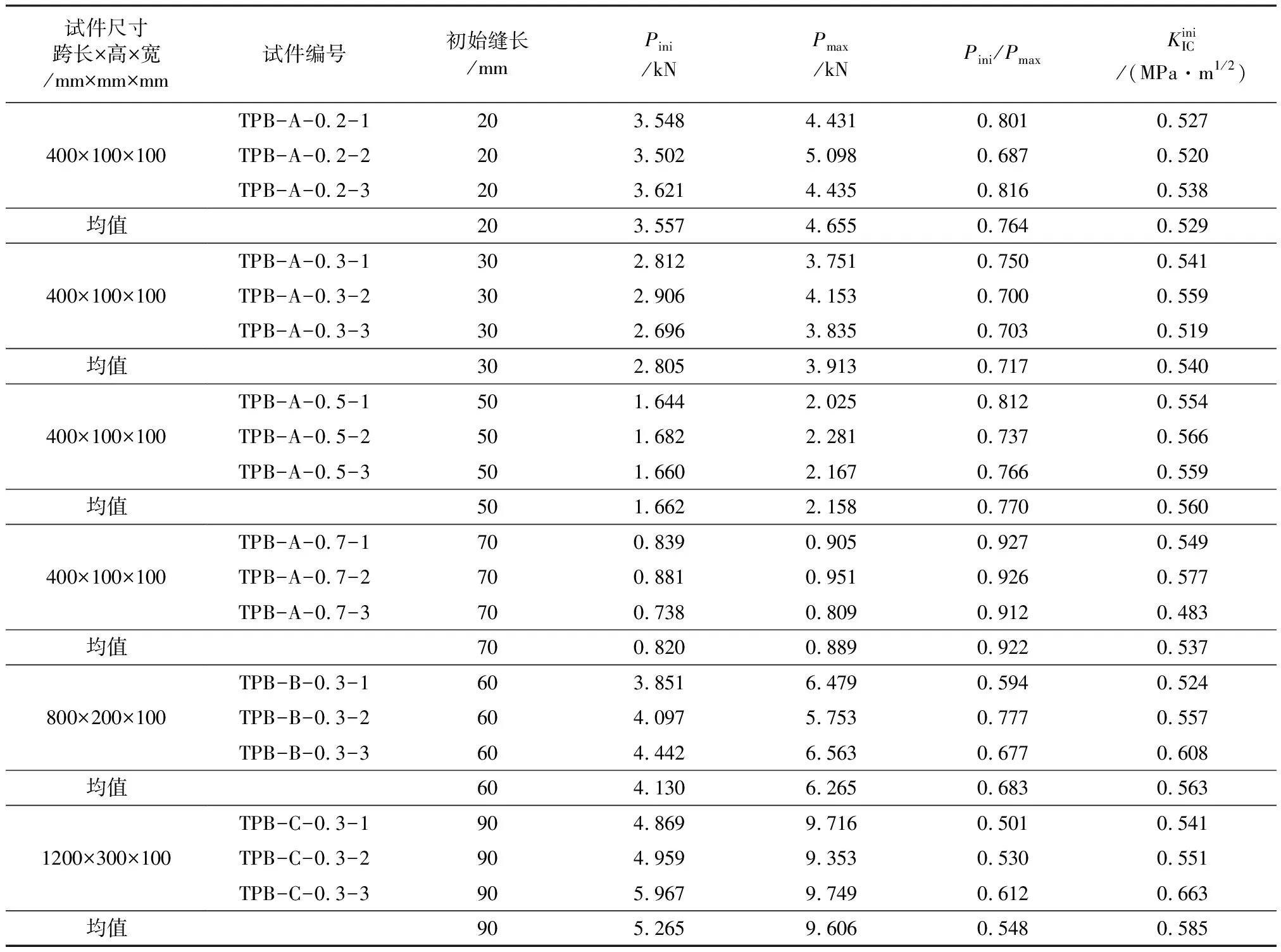
表1 三点弯曲梁试件试验结果
2.3 初始缝高比对起裂韧度的影响
图5和图6分别表示随着缝高比的变化,三点弯曲梁试件和立方体劈拉试件测定的起裂断裂韧度的变化情况。从图中可以看出,虽然测定的立方体劈拉试件的起裂韧度相比于三点弯曲梁离散性高一些,但其平均值依然表现出一定的稳定性。采用三点弯曲梁试件和立方体劈拉试件测定的起裂韧度随缝高比的增大基本保持不变且平均值较为接近,其均值分别为0.542 MPa·m1/2和0.525 MPa·m1/2。
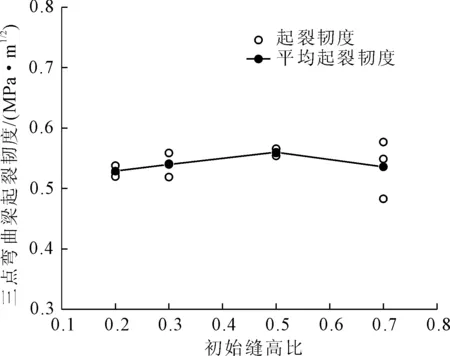
图5 不同缝高比下三点弯曲梁起裂韧度
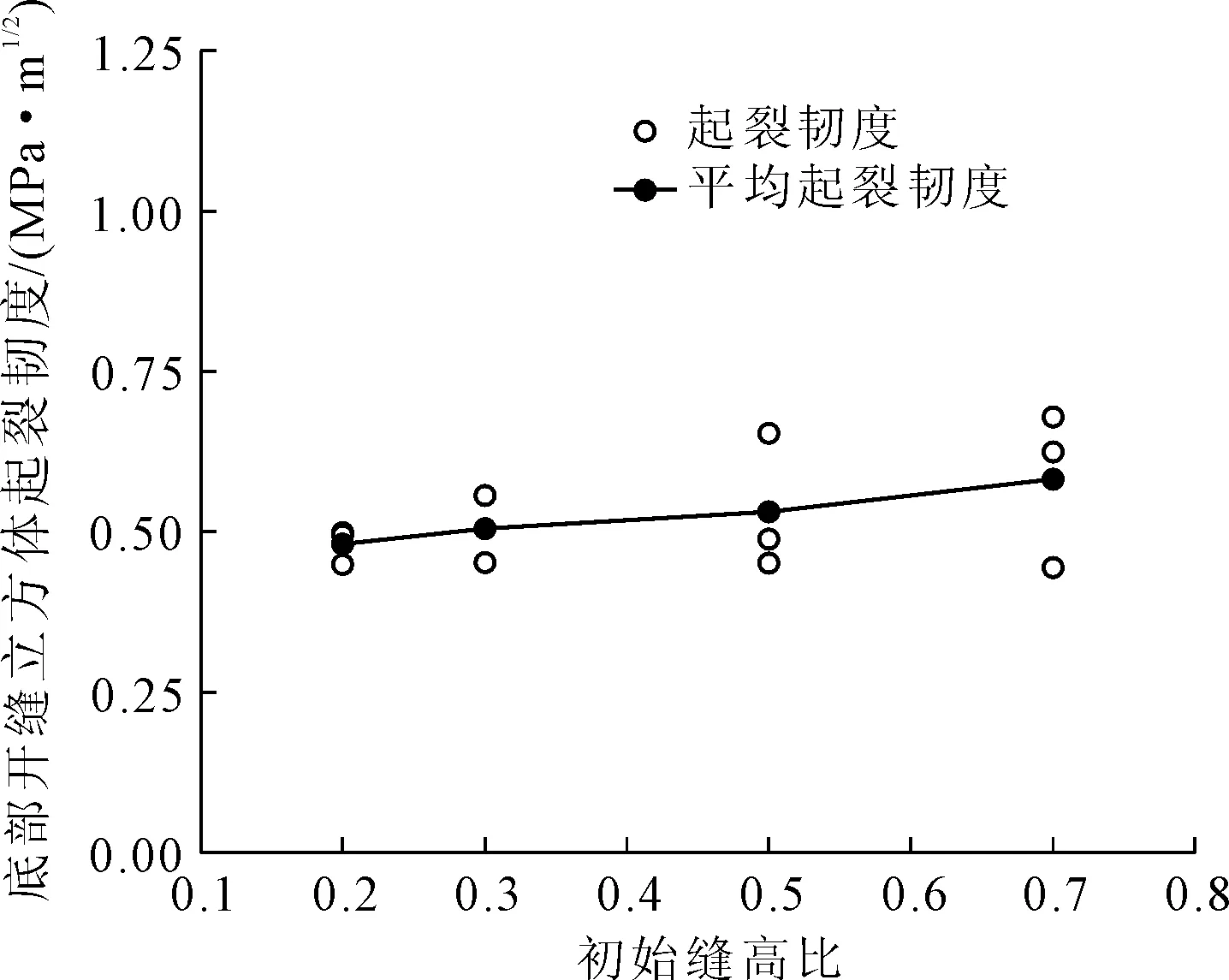
图6 不同缝高比下立方体劈拉试件起裂韧度
2.4 不同试件高度对起裂韧度的影响
图7和图8分别表示缝高比为0.3时,随着试件高度的变化,三点弯曲梁试件和立方体劈拉试件测定的起裂断裂韧度的变化情况。从图中可以看出,采用两种试件形式测定的起裂韧度随试件高度的增加基本保持不变,其均值分别为0.563 MPa·m1/2和0.503 MPa·m1/2。

表2 底部开裂缝立方体劈拉试件试验结果
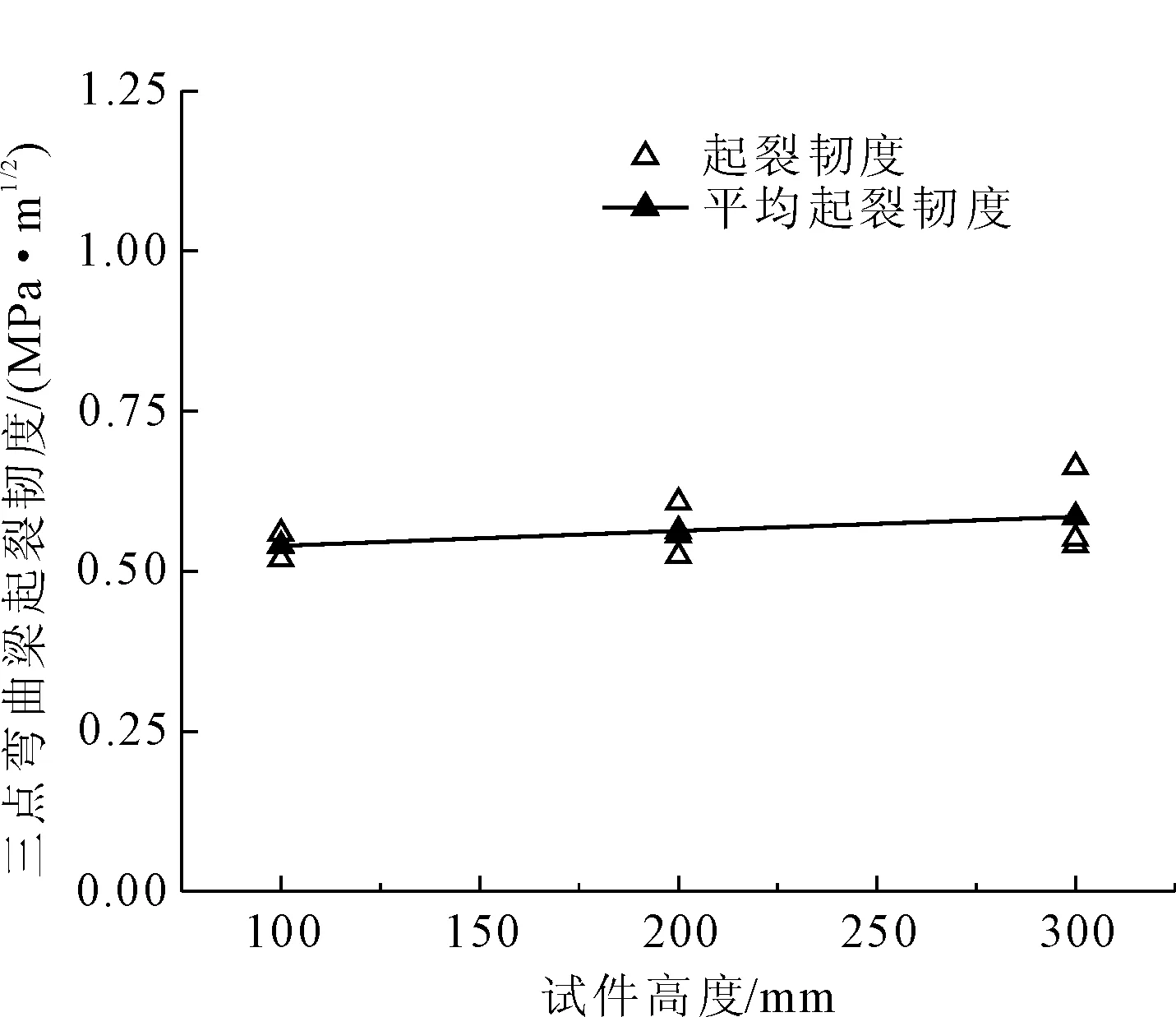
图7 不同高度下三点弯曲梁起裂韧度
在本文的研究范围内,带底部裂缝的立方体劈拉试件的起裂韧度与三点弯曲梁法测定结果基本保持一致。随缝高比或试件高度的变化,两种方法测定的起裂韧度皆无明显的变化,说明其起裂韧度受试件尺寸变化影响较小,证明底部开缝立方体劈拉试件适用于混凝土材料起裂断裂韧度的测定。

图8 不同高度下立方体劈拉试件起裂韧度
3 结 论
本文采用底部开缝立方体劈拉试件进行断裂力学试验,通过拟合缝尖应力强度因子公式,计算其起裂断裂韧度,对比三点弯曲梁的测试结果,得出如下结论:
(1) 根据试验中测得立方体劈拉试件的起裂荷载以及其初始裂缝长度、试件高度,即可采用本文拟合的应力强度因子公式计算混凝土材料的起裂断裂韧度,计算简单便于使用。
(2) 对于本文所采用的立方体劈拉试验,随着缝高比及高度的变化,测定的起裂韧度与采用三点弯曲梁方法测定的在数值基本一致,计算结果没有明显的尺寸效应,验证了该方法的有效性。
(3) 本文提出的底部开缝立方体劈拉试验方法相较于三点弯曲梁试验方法,具有试件制备简单、试验操作方便等优点,便于在实验室及工程中快速测定混凝土试件的起裂断裂韧度。
