某微型电动汽车麦弗逊前悬架设计优化
2020-03-30高坤明郭宗和于瑶瑶张裕晨
高坤明,郭宗和,于瑶瑶,张裕晨
(1.山东理工大学 交通与车辆工程学院, 山东 淄博 255049;2. 山东理工大学 材料科学与工程学院, 山东 淄博 255049)
随着我国经济和技术的不断发展,微型电动汽车以其独特的经济性和实用性,吸引了众多消费者对汽车市场的关注,特别是近些年,中国微型电动汽车的生产和销量经历了突飞猛进的增长。但是由于微型电动汽车的设计和制造成本有限,如何在保证微型电动汽车经济性的基础上,实现更高性能的设计是微型电动汽车的重要课题。目前,国内外很多学者致力于微型电动汽车悬架系统的性能优化[1-3],其中麦弗逊悬架以简单的结构设计、良好的操纵性能以及较小的占用空间成为微型电动汽车最常用的前悬架结构之一。近些年,国内外学者对麦弗逊悬架进行了更加深入的研究[4-6],上官文斌等[7]建立了一种基于麦弗逊悬架的1/4汽车模型,分别将PID控制和开关天棚控制应用于模型中,验证了模型的正确性。为解决微电动汽车麦弗逊悬架系统优化过程中多个目标的冲突性问题,多目标优化控制方法被广泛应用于麦弗逊悬架的设计优化过程[8-10],马娜等[11]以基准车辆的前束角、外倾角和侧向滑移量为设计目标,运用响应面法对悬架导向机构的硬点位置参数进行多目标优化设计,提高了电动汽车操纵稳定性和乘坐舒适性。随着群体仿生进化算法的发展,一些随机搜索方法被广泛应用到汽车悬架的优化设计中,其中遗传算法[12-13]在悬架优化中的应用尤为广泛,梁永勤等[14]运用Adams/Insight对悬架参数进行了灵敏度分析,运用遗传算法对该悬架系统进行优化,改善了悬架的运动特性。
本文以某微型电动汽车麦弗逊前悬架为实例,结合虚位移原理推导出悬架弹簧刚度的求解公式,分析前稳定杆所受到的弯曲应力和扭转应力,推导并计算麦弗逊前悬架侧倾角刚度,并通过多目标遗传算法对麦弗逊悬架参数进行仿真和验证。
1 悬架参数设计计算
1.1 悬架线刚度
悬架的线刚度是车轮保持在地面前提下车厢作垂直运动时,单位车厢位移下,悬架系统给车厢的总弹性恢复力。偏频是悬架系统的重要参数,偏频的大小直接影响乘客的乘坐舒适性,因此选取一个合理范围的偏频,可以达到乘坐舒适性和行驶稳定性的目的。由偏频可以计算出悬架线刚度,即
ka=(2·π·n)2·m
(1)
式中:ka为悬架线刚度;n为偏频;m为前悬架满载簧载质量。
1.2 弹簧刚度
悬架的弹簧刚度是悬架设计过程的重要参数之一,正确求解弹簧刚度是悬架设计的关键。虚位移原理是解决力学问题的一种方法,利用虚位移原理可以更准确地求解悬架的弹簧刚度。
麦弗逊悬架系统可以看做是一个具有理想约束的质点系,作用于质点系的所有主动力在任何虚位移所作虚功之和等于零即可使得系统平衡。
∑Fi·li=0
(2)
在麦弗逊悬架系统中,某轮胎接地点等效刚度和悬架弹簧线刚度的关系由悬架某时刻瞬心位置确定,通过瞬心的位置可以求得各个主动力在虚位移上所作的虚功。麦弗逊悬架某时刻的瞬心由三心定理作图求得,其刚度计算示意图如图1所示。
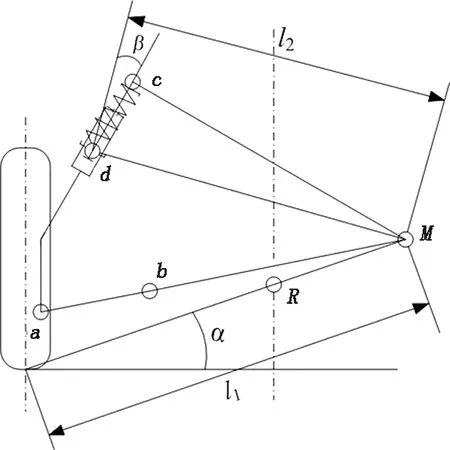
图1 麦弗逊悬架刚度计算示意图Fig.1 Schematic calculation diagram for McPherson suspension stiffness
图1中:a点为车轮轮毂和三角摆臂连接的球铰运动副;b点为三角摆臂的两个衬套与车架之间连接的等效点,是与空间直角坐标系yoz平行的平面和穿过摆臂球铰与两衬套中心连线相交的交点;c点为阻尼器和螺旋弹簧的上支座支撑点;d点为螺旋弹簧下支座支撑点。由三心定理可知,通过c点作螺旋弹簧中心线的垂直线与ab两点连线的延长线的交点M即为悬架在某一时刻的瞬心。车辆轴线和轮胎接地点到瞬心连线的交点即为悬架的侧倾中心R。
由虚位移原理可知,在麦弗逊悬架系统中所有主动力所做虚功之和等于零,即
W1+W2=0
(3)
其中:
W1=F1·l1·dθ·cosα
(4)
W2=-F2·l2·dθ·cosβ
(5)
式中:
F1=ka·l1·dθ·cosα
(6)
F2=ks·l2·dθ·cosβ
(7)
则可以求得一侧螺旋弹簧的线刚度为

(8)
1.3 横向稳定杆的线刚度
横向稳定杆结构如图2所示,当汽车转弯时,稳定杆扭转并变形,稳定杆各段变形产生的能量分别为:lT和l1段的扭转位能U1、U2,l4、l1、l2、l0段的弯曲位能U3、U4、U5、U6以及橡胶支座的变性能,且
U1=F2l2lT/4GJP
U2=F2l52l1/4GJP

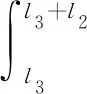
F2l2(l22+3l2l3+3l32)/6EJ
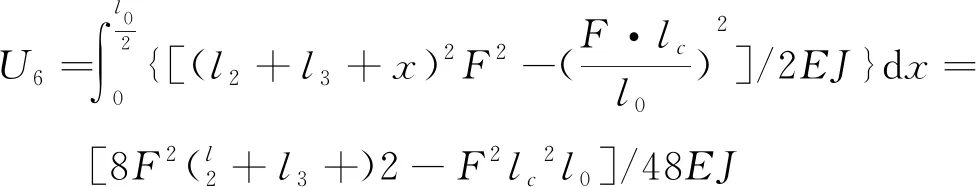
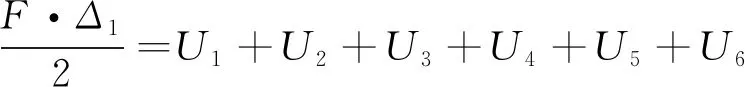
(9)

图2 横向稳定杆结构示意图Fig.2 Structural diagram of stabilizer bar
因此可以求得由稳定杆各段杆件引起的一侧变形为

(10)
又由于稳定杆橡胶支座是弹性体,在汽车转向时会产生一定的变形,引起稳定杆端点处产生一定的变形,通过力偶平衡和力与橡胶支座刚度关系可以求得橡胶支座的变形位移为Δb=Flc/l0c0,其中c0为橡胶支座径向刚度。由三角形相似可以求得由橡胶支座变形引起的稳定杆一端变形为Δ2=Flc2/l02c0,由此可以计算得到整个稳定杆的变形为Δ=2(Δ1+Δ2)。从而可以得到横向稳定杆的线刚度为
(11)
根据虚位移原理可以求得稳定杆轮胎接地点等效刚度计算公式为
(12)
式中:c为稳定杆下球销中心到瞬时转向中心的水平距离;p为轮胎接地点到瞬时转向中心的水平距离。
1.4 前悬架侧倾角刚度计算
悬架侧倾角刚度是汽车的重要参数之一,体现了汽车转弯时的转向及操纵稳定性,它由两部分组成:横向稳定杆角刚度和螺旋弹簧角刚度,计算公式如下:
(13)
式中,B为麦弗逊悬架轮距。
1.5 减震器参数计算
减振器的阻尼系数是影响汽车舒适性的重要参数,阻尼器中阻尼力F与振动速度v之间的关系为
F=δv
(14)
式中,δ为减振器阻尼系数。
在行驶过程中,车身与车轮产生相对位移,悬架阻尼器起作用,车身的振动模式为周期性衰减振动,相对阻尼系数ψ的大小用于评价振动衰减的快慢程度,ψ的表达式为
(15)
式中:C为悬架系统刚度;ms为簧载质量。
悬架阻尼系数δ为
δ=2ψmsω
(16)
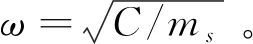
2 麦弗逊悬架系统模型
本文采用1/4的车身与车轮两自由度振动系统悬架模型,模型如图3所示。

图3 二自由度1/4汽车模型Fig.3 The 2-DOF model of quarter-vehicle body
图3中,ms和mt分别为簧载质量和非簧载质量,轮胎等效为一个刚度为kt的弹性体,悬架由螺旋弹簧ks和δ阻尼组成,xs、xt和xr分别为车身位移、轮胎位移和路面随机激励。
根据牛顿第二定律,可以建立悬架系统的微分方程。悬架系统动态模型如下:

将悬架系统模型的状态变量定义为
x=[x1,x2,x3,x4]T
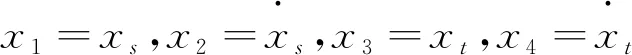
南太平洋温暖的海水中蕴藏着大量的营养物质,这也是飞鱼选择在热带及暖温带水域生活的原因。经过一个月左右的时间,小飞鱼已经长大了不少。它们逐渐强壮起来,尾鳍摆动的力量增强了,游泳的速度也越来越快。这个时候,浅海区的浮游生物已经无法满足它们生长的需要。小飞鱼必须离开珊瑚礁“幼儿园”,到更广阔的大海里去寻找食物。
则系统的状态方程为
3 多目标优化设计
3.1 目标函数选择
对微型电动汽车麦弗逊悬架进行优化时,既要考虑车辆的乘坐舒适性,还要考虑车辆的行驶稳定性。车身垂直加速度和悬架动行程是评价汽车乘坐舒适性的重要指标,在悬架动行程不超过极限要求的前提下,选择尽可能小的车身垂直加速度可以极大改善汽车的乘坐舒适性。同时车轮与地面之间的动位移直接影响车轮与地面的附着效果,可以通过降低车轮动位移改善汽车的行驶稳定性,目标函数如下:
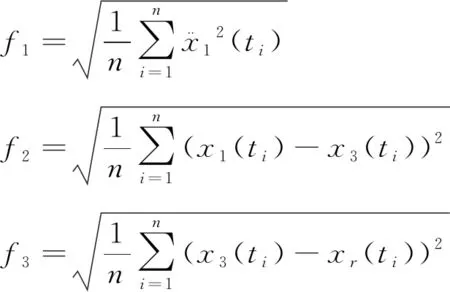
式中,f1、f2和f3分别为车身垂直加速度的均方根、悬架动行程的均方根和轮胎动位移均方根。
多目标优化方法的关键是解决目标之间的矛盾性,使多个目标能够达到均衡最优,在麦弗逊悬架的优化过程中,多个目标之间存在冲突,车身垂直加速度的优化将不可避免地导致悬架动行程和轮胎动位移性能的损失,因此多目标优化方法的应用尤为重要。
同时悬架侧倾角刚度也是汽车行驶稳定性的重要参考指标,侧倾角刚度过大或者过小都不好,当侧向惯性力等于车重的2/5时,要求车身侧倾角在2.5°~4°之间。
3.2 多目标优化问题的提出
多目标优化是多准则决策的一个领域,即涉及多个目标的数学问题的同时优化。由悬架数学模型可知,悬架设计优化的实质是具有多个变量及各类约束的非线性优化问题,电动汽车的乘坐舒适性和行驶稳定性由麦弗逊悬架中的3个参数K=[ks,δ,cw]所决定,通过选择这些参数的取值来满足3个目标,同时根据麦弗逊悬架的3个参数可以将多目标优化设计问题写成函数
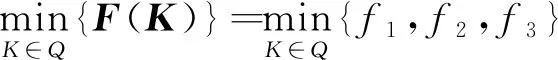
合适的适应度函数可以显著增加算法的收敛速度,各目标函数值满足约束条件下尽可能小是主动悬架优化问题所要实现的,所以直接将多目标函数转化为适应度函数即可获得较好的效果,适应度函数可表示为
Fit(K)=min{f1,f2,f3}
3.3 多目标遗传优化算法
利用进化算法求解多目标优化问题是近年来的研究热点,遗传算法将问题参数编码为染色体,然后通过迭代过程实现选择、交叉和变异,不断更新新的个体和种群,最终获得满足优化目标的染色体。在优化过程中调用遗传算法运行程序,整个优化程序的流程如图4所示。
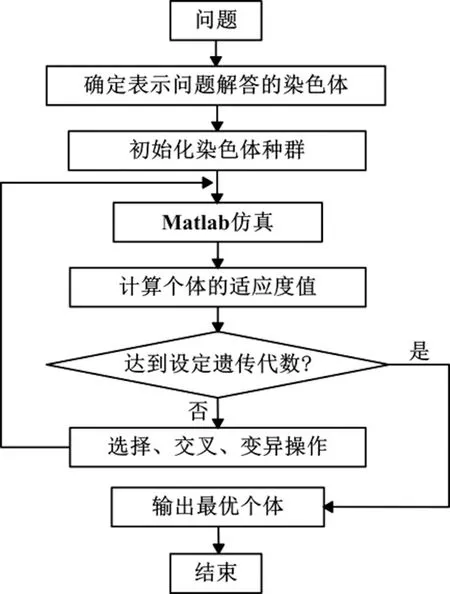
图4 遗传算法优化流程Fig. 4 Process of genetic algorithm optimization
1)染色体编码
将优化模型的3个变量依次连接成编码串,每个编码串代表种群中的1个个体,每一个个体都是可行解,初始种群数量设为100。
2)选择、交叉和变异
选择是为了从当前迭代群体中找到更加优秀的个体,并且使这些个体有更大的几率遗传到下一代,选择概率设定为0.9。
交叉是将优秀的个体进行结合,使其在迭代过程中能够更大概率地产生优秀个体,交叉概率设定为0.8。
变异可以保证种群的多样性,通过变异能够生成不同于父辈的新个体,变异概率设定为0.02。
3)终止条件
终止条件是用于实现遗传算法迭代终止的条件,通过终止条件,算法程序自动停止,并输出结束时的最优解,最大迭代次数设为300。
在应用多目标遗传算法对麦弗逊悬架进行参数优化时,选择参数K的取值范围如下:
在Matlab下建立仿真程序,仿真时间为15 s,多目标最优解如图5所示。
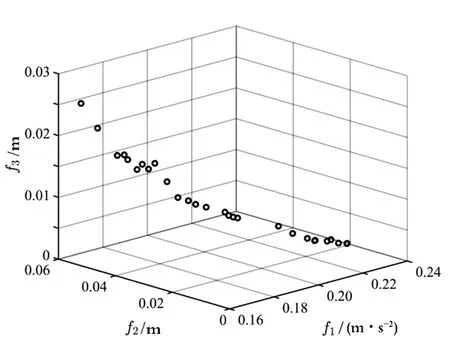
图5 多目标最优解分布图Fig.5 Distribution of multi-objective optimal solutions
4 仿真结果分析
为验证所设计的多目标遗传算法的可靠性,对某微型纯电动汽车进行实例仿真,其中ms=175 kg,mt=49 kg,kt=190 000 N/m,悬架动挠度xR=0.08 m,根据实际需求初定前悬架满载偏频为1.36 Hz。将初定前悬架满载偏频带入公式(1)~(8)可以求得螺旋弹簧线刚度为14 300 N/m,由公式(9)~(11)可以求得横向稳定杆的线刚度为44 540 N/m,由公式(14)~(16)可以求得麦弗逊前悬架减振器阻尼系数为968.5N/(m/s)。
本文采用Deshpande[15]提出的随机路面函数方程,表达式如下:
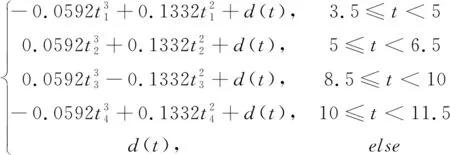
根据已建立的模型和算法,在上述路面条件下进行Matlab仿真,将优化后的麦弗逊悬架与优化前的悬架进行比较,仿真结果如图6~8所示,优化参数和目标值对比见表1和表2。
从仿真结果中可以看出,采用多目标遗传算法对麦弗逊悬架优化后,车身的垂直加速度、悬架动行程和轮胎动位移均在一定程度上得到了改善,同时麦弗逊前悬架侧倾角数值在合理的范围内。从图6和表2可以看出,与优化前的麦弗逊悬架相比,优化后悬架的车身垂直加速度的均方根值减少了29.2%,有效提高了汽车的乘坐舒适性;由图7和表2数据可以看出,悬架动行程保持在限位要求的0.08 m之内且均方根值减少了22%,降低了弹簧支座撞击限位块的风险;由图8和表2可以看出,轮胎动位移的均方根值减少了 15.8%,有效改善了汽车轮胎的抓地能力,减少了侧向力的产生,从而提高了汽车的行驶稳定性。

图6 车身垂直加速度对比曲线Fig.6 Vertical acceleration curve of the vehicle body
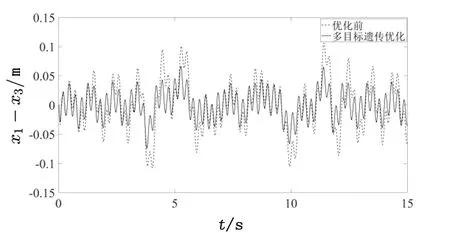
图7 悬架动行程对比曲线Fig.7 Suspension travel comparison curve
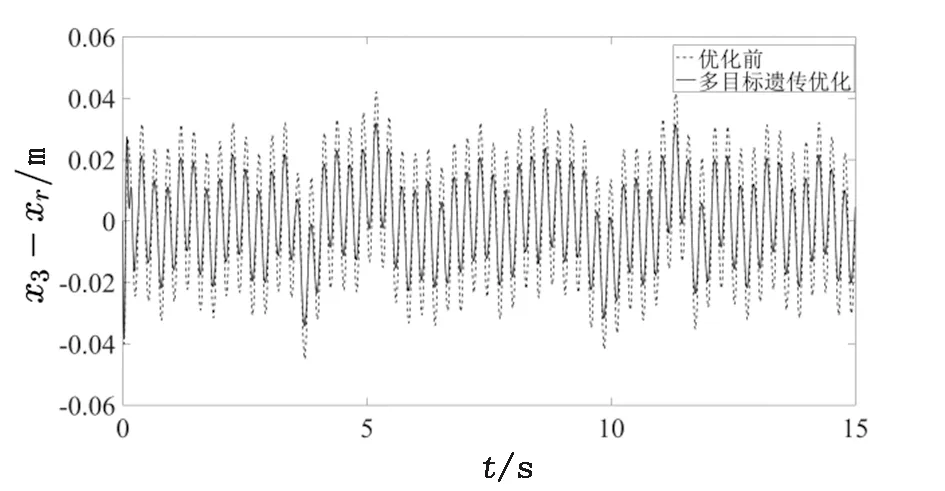
图8 轮胎动位移对比曲线Fig.8 Tire dynamic displacement curve
表1 优化前后悬架参数
Table.1 Suspension parameters before and after optimization

参数弹簧刚度/N·m-1偏频/Hz稳定杆线刚度/N·m-1阻尼系数/N·(m·s-1)-1侧倾角刚度/N·m·rad-1优化前14 3001.3644 540968.54.158×1010优化后12 8611.2541 226812.81.362×1010
表2 优化前后目标值
Tab.2 Target value before and after optimization

目标值f1/(m·s-2)f2/mf3/m侧倾角/(°)优化前0.7680.0860.0380.86优化后0.5440.0670.0322.93
5 结束语
本文结合虚位移原理推导出麦弗逊悬架弹簧刚度和稳定杆线刚度,计算了麦弗逊前悬架侧倾角刚度和减振器阻尼系数,建立了汽车1/4悬架物理模型,并运用多目标遗传算法对麦弗逊悬架系统进行了参数优化。仿真结果表明,与优化前的麦弗逊悬架相比,车身垂直加速度明显减小,悬架动行程和轮胎动载荷也得到了改善,减振效果显著,提高了汽车的乘坐舒适性和行驶稳定性。
