基于名义应力法的结构疲劳评估方法

2020-03-29刘海涛陈海波李宝珠

中国金属通报 2020年18期

刘海涛，陈海波，李宝珠，张帅

（航空工业西飞民机，陕西西安 710089）

飞机在寿命周期内，机体结构承受交变载荷循环，在循环载荷作用下机体结构可能会由于疲劳损伤而产生裂纹[1]。结构的疲劳性能与结构的构型、材料、制造工艺以及结构所受的载荷状态等因素有关，目前计算结构寿命主要应用名义应力法、基于名义应力法的应力严重系数法以及由美国波音公司提出的细节疲劳额定值（DFR）法等。名义应力法计算有限疲劳寿命需要各种应力集中系数下各材料的S-N 曲线或等寿命曲线，虽然目前已积累了大量的S-N 曲线，但是由于实际结构和载荷的复杂性[2]，导致一些具体的结构很难有合适的曲线，而DFR 法可以根据结构形式及载荷状态确定分析结构的疲劳额定值，但是其曲线的拟合需要大量的试验数据支持，成本巨大，耗时较长，目前国内学者做了大量研究以快速得到结构的疲劳额定值，郑修麟[3]对Manson-Coffn 应变疲劳公式做了修正，文献[4]中针对钉传载结构计算疲劳额定值，假定基准板的最大应力和结构的最大应力相等，适用范围较小，文献[5]提出一种考虑尺寸效应的疲劳预测方法，需确定裂纹可能萌生区域大小且其中疲劳强度通过试验得到。

本文提出一种基于传统的名义应力法和等寿命转换，通过统计总结S-N 曲线中各参数中的对应关系模型而得到的疲劳寿命计算方法，并与试验结果进行对比分析，表明该方法在工程中评估结构的疲劳性能的可行性。

1 传统名义应力法疲劳模型

目前疲劳寿命模型主要是基于S-N 曲线拟合推导得到，1920年由Basquin 用公式σa=C×Rn表述了有限寿命的S-N 曲线。通常一条完整的S-N 曲线可分为三段，即低周疲劳区（LCF）、高周疲劳区（HCF）和亚疲劳区（SF）[2]，见图1。为了摸索S-N 曲线的变化规律，人们进行了不少的工作，目前用来近似表达S-N 曲线的经验公式一般有4 种，分别为幂函数表达式、指数函数表达式、三参数函数表达式和以及四参数函数表达式[6]以及其他形式的Weibull 公式。

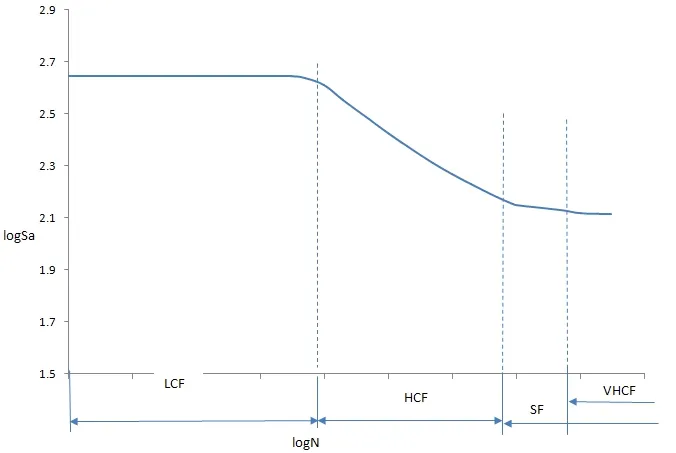
图1 S-N 曲线图

现代飞机结构的寿命普遍分布在104～106的高周疲劳区（图1 中的HCF 区域），因此现代飞机的疲劳寿命分析主要是基于S-N 曲线的高周疲劳区进行计算的，在该范围内，疲劳寿命与循环名义应力幅aS的关系通常用Basquin 幂函数方程[7]表示，即公式（1）：

随着人们大量的工作，发现该式在短寿命区是适用的，而当疲劳寿命较长时，试验结果与公式（1）存在偏离，因此本文根据工程计算实际情况，采用三参数幂函数表达式，即weibull 公式：

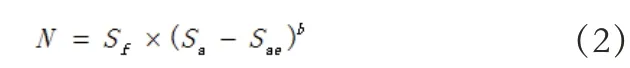
2 基于传统疲劳模型的工程推论

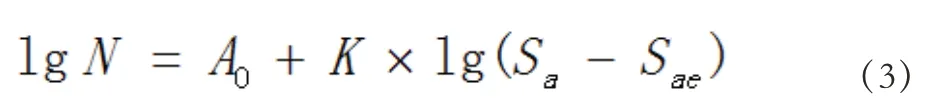
K 为S-N 曲线的斜率，根据郑修麟[8]通过总结比较Coffn 和Martin[9]的分析工作，结合试验结果分析总结，得出K=-2，波音公司提出标准S-N 曲线的斜率参数，对于铝合金材料s=2[10]，即斜率K 值为-3.2，黄啸等[11]关于斜度参数对疲劳额定值的影响进行了分析，斜率的取值对于额定值的影响较大。对于新的材料，斜率K 值需进行测定，这里暂将K 值作为定值进行下面的公式展开，通过公式（3）可见只需确定0A 的值，即可得到在一定应力比或者平均应力下，通过结构载荷的应力幅值aS 和疲劳应力极限快速计算结构疲劳寿命的方法。现以R=0 情况下给定结构50%可靠度的S-N 曲线进行计算，在直线上取一点现代民航飞机结构的中值寿命已多数达到25 万次及以上，因此本文取，对应的即为结构在R 比为0，寿命为3*105的情况下的最大应力（ Smax），将点代入方程（3）中，得公式（4）：

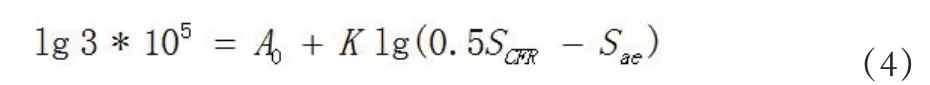
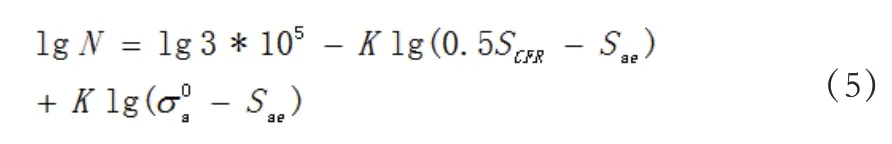
采用等寿命转换公式进行不同R 比的应力转换，陈先民等[12]结合不同的等寿命曲线分别建立了数学模型，为工程应用提供参考，樊俊玲[13]对Gerber 型等寿命曲线导出的疲劳寿命计算方法同Goodman 公式进行了比较，本文采用工程上常用的Goodman[14]公式（6）：

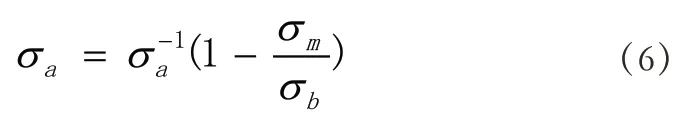
对于R 比为0 的等寿命转化为：

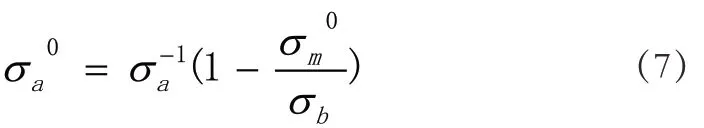
3 分析参数关系模型的建立及推论

通过公式（8）可见，在确定了一个结构的载荷谱之后，结构的寿命计算需要确定参数 SCFR、和K 值，K 值为定值或由试验测定，若通过试验测定具体结构的参数 SCFR、值要耗费大量人力物力和时间成本，因此确定参数 SCFR、值与结构特性之间的关系便可满足工程中快速评估结构疲劳性能的需要，将带来重大的经济效益。目前国内外研究者已经做了大量的试验和研究工作，本文通过整理试验结果，提出具体结构在给定应力比和寿命下的最大应力与结构疲劳细节点的应力集中系数接近幂函数关系，并针对寿命为3*105所对应的 SCFR、与结构特性的关系模型，提出函数关系见公式（9）：为关于材料的参数。根据文献[15]中的试验数据和S-N曲线，整理了几种国内外航空铝合金材料的参数值且画出拟合曲线见图2，统计整理并给出统计学相关系数R，见表1。

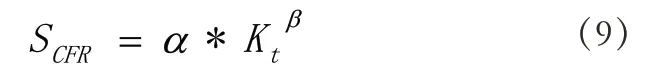
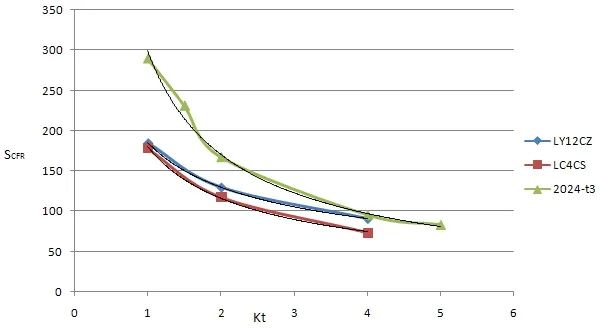
图2 不同结构对应的额定值及趋势线

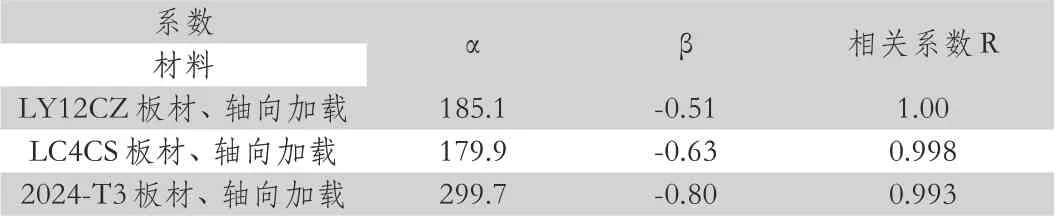
表1 部分铝合金的额定值拟合参数

同样整理几种国内外航空铝合金材料的参数值且画出拟合曲线，统计整理并给出统计学相关系数R，见表2，便于以后计算分析时使用。

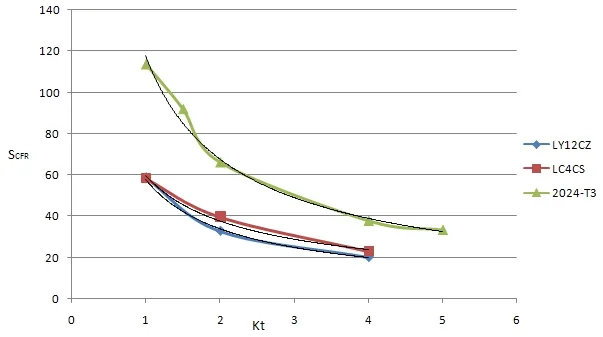
图3 不同结构对应的疲劳极限及趋势线

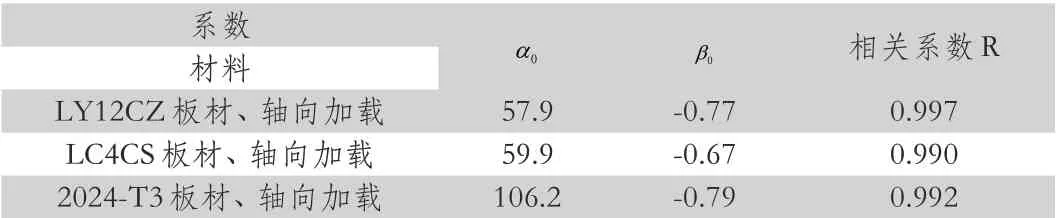
表2 部分铝合金的疲劳极限拟合参数

疲劳寿命公式（8）是根据材料标准试验总结的S-N 数据得到的，而在计算飞机结构的疲劳寿命时需要进行多因素的修正，影响结构疲劳性能的因素很多且很复杂，通常包括材料因素、几何因素、表面状态、残余应力、工作条件等，需要将拟合后的S-N曲线进行影响因素的修正。本文不对影响疲劳强度的因素进行研究，进一步的资料需要查阅相关的资料或在以后的试验研究中进行探讨。

4 算例

为了验证该疲劳分析方法的可行性，现针对具体结构通过公式计算在不同的载荷情况下的寿命，同试验结果的拟合曲线进行比较，并对结果进行说明。

4.1 国产LY12-CZ 铝合金材料疲劳试验

带有中心圆孔和长圆孔，板厚2.5mm 的板材见图4，材料为LY12-CZ 铝合金，载荷幅值等幅谱疲劳试验[16]。建立细节有限元模型，计算两个孔周围的应力分布情况，见图5，比较圆孔和长圆孔边的最大应力以及应力分布情况，可以确定圆孔为疲劳性能最薄弱位置，这在试验中得到证实。

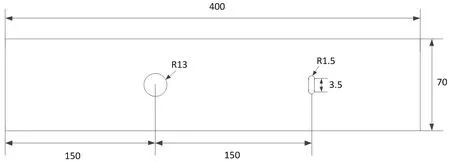
图4 试验件结构模型示意图

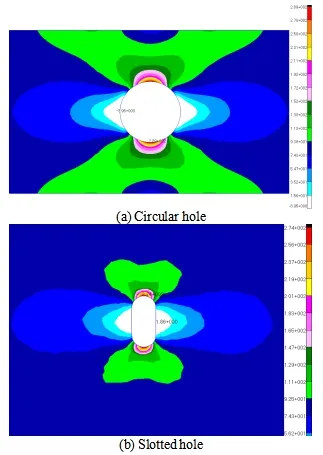
图5 孔周围的应力分布

针对圆孔进行疲劳分析，通过有限元结果可以计算得到试验件应力集中系数，根据表1 和表2 中读取LY12-CZ 铝合金材料对应的系数，取K=−2，通过公式(8)计算得，与试验结果进行对比，结果见表3，可见计算结果与试验值相当。

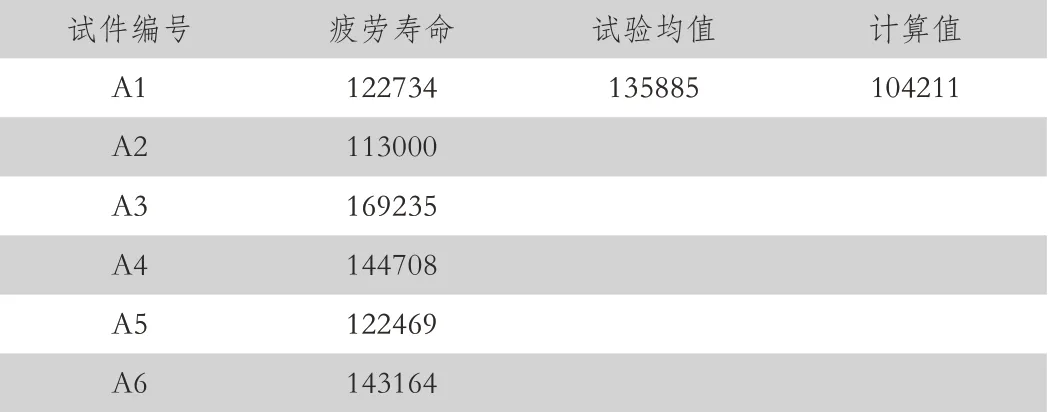
表3 LY12-CZ 铝合金的疲劳试验数据比较

4.2 国外2024-T3 铝合金材料疲劳试验

中间具有凹槽的2024-T3 铝合金板材，板材厚度2.3 毫米，应力集中系数为4，即Kt=4。

从表1 和表2 中读取2024-T3 铝合金材料对应的系数：。通过公式（8）计算在不同的载荷情况下的寿命，同试验结果的拟合曲线[17]进行比较，结果见图4。

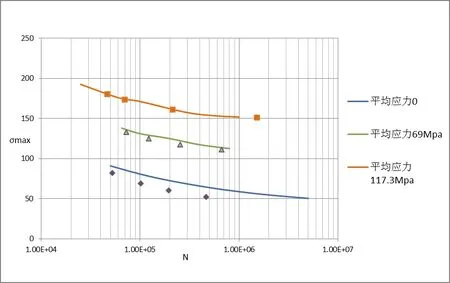
图6 2024-T3 计算结果与试验拟合曲线的比较

通过图6 可见计算数据与材料曲线拟合度可以满足工程评估需要，但不同平均应力下拟合度不同，平均应力0Mpa 下的计算结果比试验数据偏保守，这跟Goodman 等寿命转换公式低估平均应力的影响是一致的[7]。后续的研究中，将继续深入研究不同的载荷水平下的等寿命转换关系，和各影响疲劳性能的因素，以对评估方法进一步修正，提高寿命预测精准度。