筒式武器有限空间内发射流场特性研究*
2020-03-29郭保全栾成龙李鑫波
丁 宁,郭保全,黄 通,栾成龙,李鑫波
(1 中北大学机电工程学院,太原 030051; 2 中北大学火炮技术研究中心,太原 030051)
0 概述
单兵筒式武器作为一种步兵肩射武器,具有质量轻、机动性高、隐蔽性强、 低后坐或无后坐等优点, 可以进行防空反导、反装甲和摧毁敌方防御工事等作战任务,有利于在战壕、巷子、居所等狭隘作战环境内实施作战[1-2]。在我国单兵器发展规划中,单兵筒式武器因具有“有限空间发射”的能力被着重强调[3]。
探究筒式武器在有限空间内发射的流场特性对进行有限空间发射技术的研究有重要的指导意义。目前,国内外学者对单兵筒式武器“有限空间内发射”技术开展了大量研究,主要集中在如何减少后喷流场的冲击波、噪声、火焰等,例如通过在发射筒尾部放置液体、塑料碎块等,来达到降冲击、消焰降噪的目的[4-6];且对于筒式武器后喷流场的研究主要是针对自由射场开展的[7-10]。而针对筒式武器在有限空间内发射后喷流场特性研究较少,未能探究后喷火药燃气冲击波经过墙壁面反射后空间内流场的变化特性。
文中以某82 mm单兵筒式武器为例,通过构建其在有限空间内发射后喷流场数值仿真模型,利用ANSYS Fluent软件对后喷流场进行数值模拟。研究了后喷火药燃气冲击波与壁面相互作用引起的流场变化,并探讨了在不同发射环境内发射近、远场流场压强变化规律。该研究对实现有限空间发射技术以及预测冲击波对炮手的危害有一定的指导意义。
1 计算模型及网格划分
1.1 基本假设
筒式武器后喷流场存在复杂的火药燃气与挡板碎片耦合过程,为了方便计算模型的建立以及减少计算量,作出以下假设:
1)将火药燃气后喷过程,由实际三维问题简化成便于建模计算的二维仿真模型。
2)高温高压火药燃气作为理想气体考虑,忽略其化学反应过程。
3)不考虑火药燃气和喷管壁面的热量交换。
4)忽略火药燃气压破药室挡板的过程以及挡板碎片对后喷流场的影响。
1.2 计算模型
如图1所示,在数值计算模型中将喷管入口端设置为压力入口边界条件,窗户设置为压力出口边界条件,喷管内外壁面、发射筒外壁面、地面、墙顶、后壁面设置为壁面边界条件。

图1 有限空间发射后喷流场计算模型
为分析筒式武器后喷流场变化规律,设立监测点如图2所示。其中,p1、p2、p3为远场监测点,设于发射筒轴线上,分别距离喷管尾端1.2 m、2.4 m、3.8 m,主要用于监测空间内远场压力变化。r1、r2、r3为近场监测点,设于以喷管入口为中心,半径为0.5 m的圆弧上,其与喷管入口中心的连线与发射筒轴线的夹角分别为90°、60°、30°,主要用于检测空间内近场压力变化。

图2 监测点位置示意图
1.3 网格划分
本模型全网格采用结构化网格。由于尾喷管内部涉及超高速流动,为保证计算准确,对喷管喉部和其出口区域网格进行加密处理。在计算后期,冲击波会与墙壁面存在碰撞反射现象,因此对墙壁面附近的网格也进行加密处理。局部网格如图3所示。

图3 计算模型局部网格
1.4 边界条件及算法
文中以某筒式武器内弹道数据为入口边界条件,入口压力取内弹道膛压曲线,入口温度取内弹道膛温曲线,如图4、图5所示。

图4 入口压力曲线
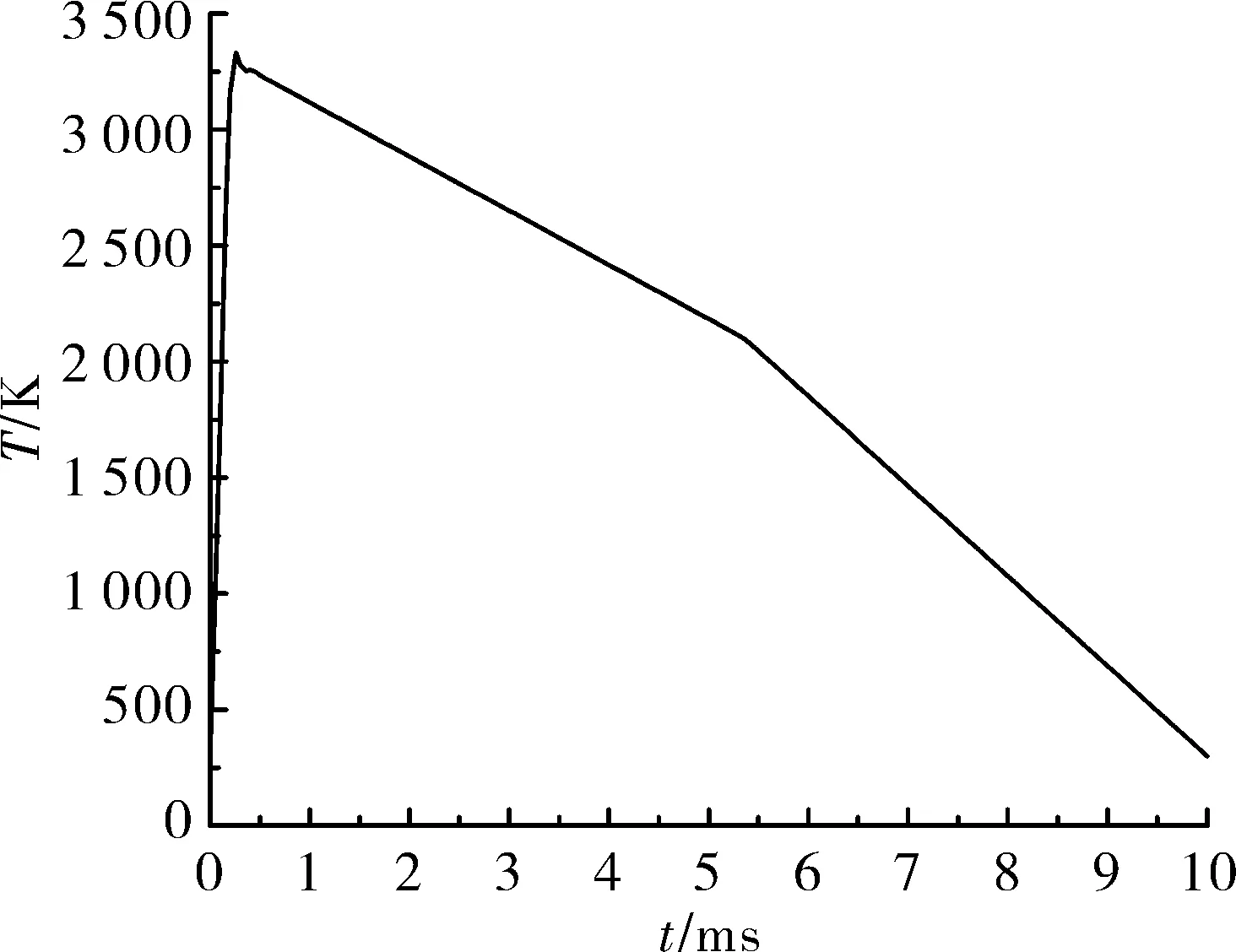
图5 入口温度曲线
出口压力取一个大气压,出口温度取300 K;壁面函数采用标准壁面函数,壁面不考虑热量交换;对计算域进行初始化时,计算域压力取一个大气压,温度取300 K。求解方法采用基于密度的耦合求解方法,对二维控制方程的离散采用有限容积法,对导数项采用二阶迎风格式,控制方程中的湍流模型采用Realizablek-epsilon模型。
2 仿真分析
2.1 后喷流场分析
根据流场仿真结果,筒式武器后喷流场可分为3个阶段:初始波系形成阶段、冲击波反射阶段、紊乱阶段。
第一阶段:发射药点燃后,燃气射流压缩药室空气,生成一系列压缩波,压缩波不断叠加逐渐形成为一道强激波,从喷管喷出。如图6所示,火药气体从喷管迅速释放,形成非定常欠膨胀射流结构,强激波不再受到喷管限制作用迅速膨胀形成球形的火药燃气冲击波,同时由于高速火药燃气射流的从喷管尾部喷出对周围空气的卷吸作用,在喷管出口周围形成两个低压漩涡。如图7所示,0.7~3 ms之间,冲击波不受空间约束自由膨胀,呈球形不断往后运动,直到冲击波与墙顶、地面碰撞,第一阶段结束。该阶段后喷流场与在自由射场发射后喷流场规律相同。

图6 0.7 ms后喷流场压力云图

图7 3 ms后喷流场压力云图
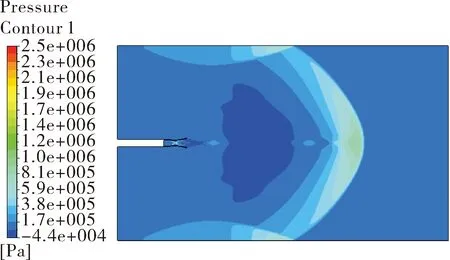
图8 4 ms后喷流场压力云图
第二阶段:如图8所示,随着冲击波的不断膨胀,球形冲击波直径大小超过3 m,波面与地面、墙顶发生碰撞,形成弓形反射波。弓形反射波波与原冲击波相碰撞叠加。如图9所示,在6.5 ms左右,冲击波与后壁面碰撞反射,由于后壁面与冲击波运动方向垂直,后壁面出现较高压强峰值。
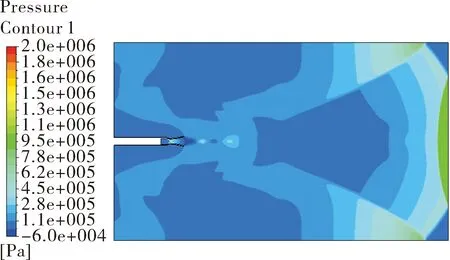
图9 6.5 ms后喷流场压力云图
第三阶段:如图10、图11所示,7 ms左右,冲击波与墙顶、地面碰撞形成的弓形反射波和冲击波与后壁面碰撞形成的强反射波交汇,逐渐形成一高压紊乱气流团。紊乱气流团逐渐向窗外移动,在16 ms左右,紊乱气流作用于近场监测点。

图10 7 ms后喷流场压力云图
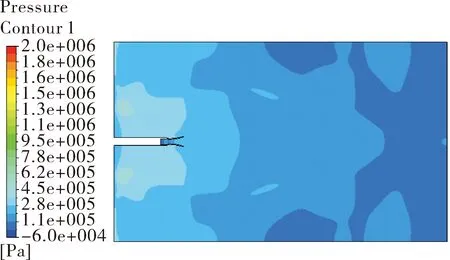
图11 16 ms后喷流场压力云图
2.2 近、远场压强变化规律
图12描述了近场监测点压强随时间变化规律。在0~3 ms之间,球形火药燃气冲击波经过监测点,3个监测点分别出现压强峰值并迅速跌落,并且越靠近轴线,其压强峰值越大。在5~10 ms之间,由于冲击波与地面、顶面碰撞形成弓形反射波,导致近场监测点压强升高并产生锯齿状波动。但由于与地面、墙顶产生碰撞的冲击波波面强度较弱,因此产生的弓形反射波也较弱。在16 ms左右,冲击波与地面、墙顶碰撞形成的弓形反射波和与后壁面碰撞形成的反射波相互叠加形成的高压紊乱气流团逐渐向窗外移动,经过近场监测点从而引起高压峰值。随着紊乱气流团从窗口逐渐消散,近场监测点压强逐渐趋于一个大气压。
图13描述了远场监测点压强随时间变化规律。在0~7 ms之间,火药燃气冲击波依次经过监测点,出现高压峰值, 随着冲击波运动,能量消耗,峰值逐渐减小。7~12 ms之间,冲击波与后壁面碰撞,导致远场监测点压强峰值回升,产生齿型波动,监测点越靠近后壁面,回升越高,波动越剧烈。之后,远场压强逐渐稳定到一个大气压。

图13 远场不同监测点压强变化曲线
2.3 不同发射条件下流场压强变化规律比较
为更好探究筒式武器在有限射场发射后喷流场特性,对其在自由射场发射的后喷流场进行仿真分析。图14、图15描述了筒式武器在有限射场与在自由射场发射时相同位置监测点压强变化规律。其中,r1、p3为有限射场内监测点,r′1、p′3为同位置自由射场内监测点。r1、r′1为炮手点,p3、p′3为近壁点。由图14可知,0~3 ms内,由于后喷流场处于初始波系形成阶段,两种发射条件下炮手点压强变化一致。 在7 ms左右,由于燃气射流对周围空气的卷吸作用,r1曲线出现低压峰值,之后炮手点压强开始回升并逐渐稳定在一个大气压。在有限射场内,5~10 ms阶段,由于冲击波与地面、墙顶碰撞形成的弓形反射波经过炮手点,使压强升高,其峰值为1.5个大气压左右。在16 ms左右,由反射波引起的高压紊乱气流团经过炮手点,出现高压峰值,值为4个大气压左右,为自由射场峰值的2.5倍。
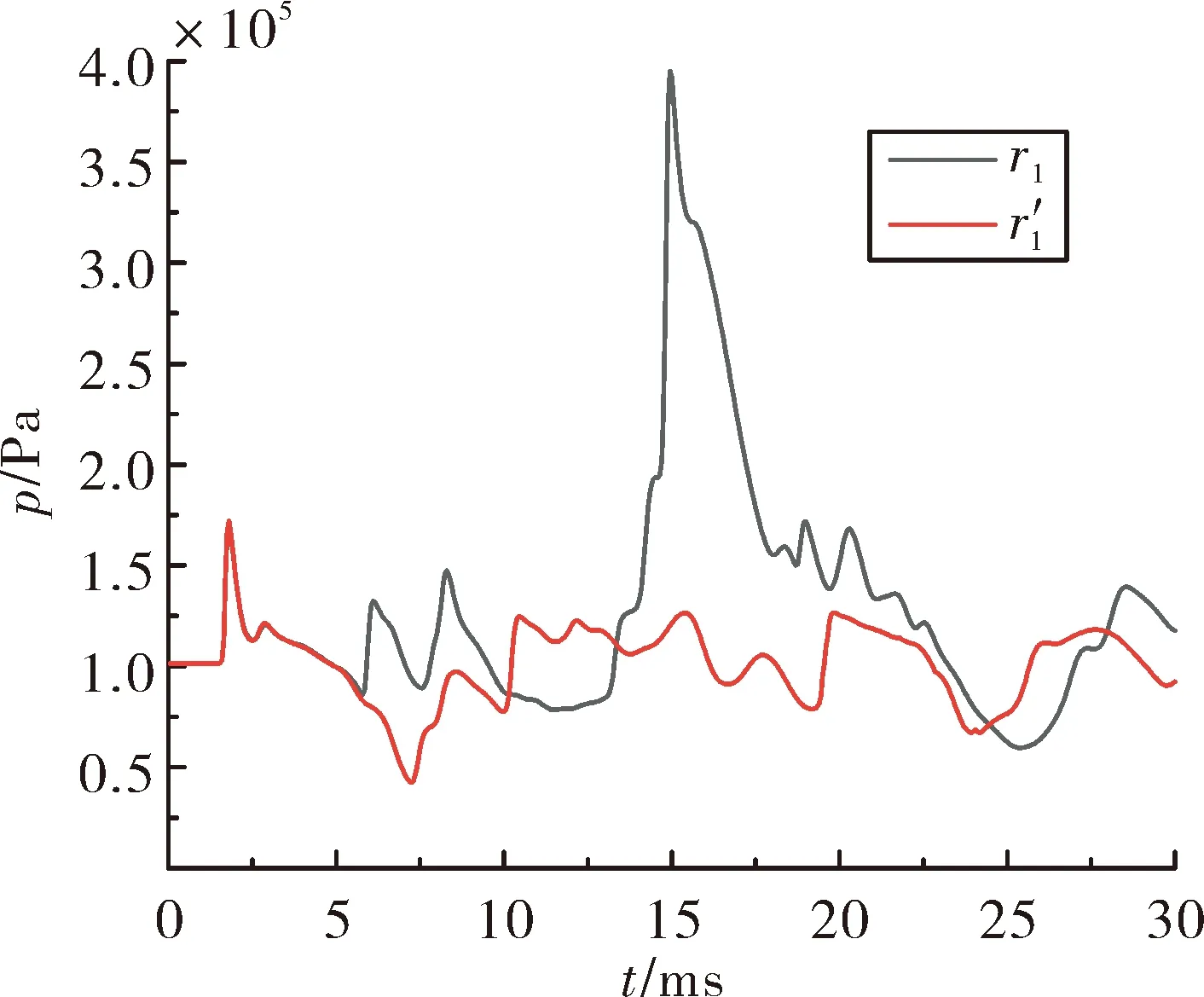
图14 不同发射环境下炮手点压强变化曲线
由图15可知,在0~7 ms之间,不同发射条件下近壁点压强变化规律基本相同。在有限射场内,7 ms左右,冲击波与后壁面垂直碰撞形成的较强反射波经过近壁点,该点压强回升并出现齿形波动。当较强反射波完全通过该点,该点压强迅速回落。有限射场与自由射场的流场相比,近壁点压强峰值提升较小,是因为入射冲击波本身强度越低,反射波强度提升就越小[11-12]。

图15 不同发射环境下近壁点压强变化曲线
3 结论
通过对单兵筒式武器有限空间发射后喷流场进行分析,得出以下结论:
1)筒式武器有限空间内发射后喷流场可以分成3个阶段:初始波系形成阶段、冲击波反射阶段、紊乱阶段。第一阶段:火药燃气从喷管高速喷出,形成球形火药燃气冲击波,并在喷管尾部形成两个低压漩涡;第二阶段:冲击波首先与地面、墙顶碰撞形成弓形反射波,然后与后壁面碰撞反射形成较强反射波;第三阶段:弓形反射波与强反射波相互作用形成高压紊乱气流团逐渐向窗外移动。
2)筒式武器在有限射场内发射时,冲击波与地面、墙顶碰撞产生的弓形反射波对近场影响较小,幅值在1.5个大气压左右;冲击波与后壁面碰撞产生的反射波对远场监测点影响较大,幅值在2.5~6.5个大气压左右;高压紊乱气流团对近场影响较大,幅值在4个大气压左右。
3)筒式武器在有限射场与在自由射场相比,炮手点压强峰值出现在发射结束之后,是由高压紊乱气流团经过引起的,峰值是自由射场的2.5倍左右,近壁点高压峰值提升较小。
