基于非线性车辆模型的行驶状态与路面附着系数估计
2020-03-28张航星路永婕2张俊宁
张航星, 路永婕2, 张俊宁
(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.河北省交通安全与控制重点实验室,河北 石家庄 050043)
0 引言
对车辆行驶状态和路面附着系数的准确估计,是实现汽车主动安全控制的重要瓶颈问题[1],车轮纵向速度、侧向速度、质心侧偏角是评价汽车安全行驶状态的重要变量,路面状况估计主要是针对轮胎与路面之间附着系数的估计。汽车行驶中这些待估计的状态变量,虽然都可以通过传感器直接测得,但硬件成本较高,测量精度的耐久性差,测量的实时反馈存在时滞。理想的状态估计算法,不但可以减少传感器数量,降低系统成本;也可提高响应速度和可靠性,降低对硬件制造精度和工艺要求。所以,寻求理想的估计算法一直是国内外学者研究的热点问题[2-8]。Hahn O et al[9]和Han K S et al[10]提出了一种根据车辆侧向运动状态来估计轮胎-路面附着系数的算法,将轮胎侧向力参数化为与侧偏角、附着系数、法向力和侧偏刚度相关的函数,它是利用差分GPS系统和陀螺仪的测量值实现对轮胎-路面附着系数和轮胎侧偏刚度系数的识别参数实时算法,并验证了该算法可以有效地识别干燥路面和湿滑路面。Tanelli M[11]基于摩擦曲线的经验拟合估计当前道路状况,并结合速度估计算法提出了在线算法,测试了该算法无论是在复杂程度和估计精度上均适用。Chen L et al[12-13]建立了采用Dugoff轮胎模型的非线性三自由度车辆模型,基于无迹卡尔曼滤波(Unscented Kalman Filter,UKF)理论,将路面附着系数估计和车速估计结合起来,实现对车辆纵向力、垂向力、滑移率和路面附着系数的估计,但UKF算法的缺点在于其参数的选择问题尚没有得到完全解决,且参数的选择受系统噪声的影响。对于非线性系统滤波问题,常用的处理方法是利用线性化技巧将其转化为一个近似的线性滤波问题,其中应用最广泛的方法是扩展Kalman滤波(Extended Kalman Filter,EKF)方法。
本文的研究对象是重型四轮汽车,建立了三自由度四轮整车模型,并验证了该模型的合理性。采用扩展卡尔曼滤波实现了汽车各状态变量及路面附着系数的估计,轮胎模型采用了Dugoff轮胎模型[14]。从Simulink仿真模型中获取各车轮转速和前轮轮胎转角,通过Matlab编程实现EKF算法,算法估算得到的汽车状态参量和路面附着系数与设定值进行仿真对比。通过在设定的典型双移线工况下,对比EKF算法得到的估计值和Simulink仿真值,验证了估计算法的有效性。
1 非线性三自由度车辆动力学模型
1.1 三自由度车辆转向动力学模型

图1 非线性三自由度车辆转向模型
车辆在车轮牵引力作用下做转向运动时,因侧向加速度的出现,轮胎产生侧偏力,随着轮胎滚动,车体出现侧偏现象;由于前轮和后轮的垂向载荷分配不同,所以轮胎与路面相对运动产生的附着力不同,导致车辆会出现横向摆动,轮胎纵向行驶力也随之发生变化。为了能够准确描述车辆转向时的行驶状态和附着力,取纵向位移、侧向位移、横摆角速度3个方向的运动建立整车模型,非线性三自由度四轮车辆转向运动学模型如图1所示。
由图1的车辆模型,可得到车辆在转向行驶下的运动微分方程,如式(1)和式(2)。
(1)
(2)
当车轮转向角较小时,有式(3)和式(4)的运动学关系。
(3)
(4)
由此,可以得到车轮纵向和横向加速度的表达
(5)
(6)
横摆角加速度可以表示为

(7)
式中,m为车身质量;vx为车辆纵向速度;vy为车辆侧向速度;r为车辆横摆角速度;Iz为车辆横摆转动惯量;ax为车辆纵向加速度;ay为车辆横向加速度;a为前桥至车辆质心处的距离;b为后桥至车辆质心的距离;δ为前轮转角;Tf、Tr分别为前轮和后轮的轮距;Fx_fl、Fy_fl、Fx_fr、Fy_fr、Fx_rl、Fy_rl、Fx_rr、Fy_rr分别为前后轮左右两侧轮胎的纵向力和侧向力。
各轮侧偏角可表示为
(8)
各轮胎纵向速度、侧向速度可表示为
(9)
车辆在转向时各个轮胎的垂向力可表示为
(10)
1.2 Dugoff非线性轮胎模型
目前,轮胎稳态模型可以分为理论模型、经验模型和半经验模型。理论模型是根据轮胎变形的物理过程建立的轮胎模型,轮胎的物理结构及材料特性非常复杂,直接决定了轮胎力学特性的研究难度。Dugoff轮胎模型是一种描述轮胎纵滑侧偏的模型,即假定轮胎与路面的接触区近似为矩形,其结构简单,参数物理意义明确,该模型中,侧向力与纵向力和轮胎-路面附着系数具有明显的直接关联,这对实现车-路之间的附着系数估计提供了重要的途径,该模型原理如图2所示。

图 2 Dugoff轮胎模型原理图
Dugoff轮胎模型的轮胎纵向力、侧向力表达为
(11)
(12)
其中

(13)
(14)
式中,μ为轮胎与路面附着系数;Cx、Cy为轮胎纵滑及侧偏刚度;ε为速度影响因子,与轮胎结构及材料有关,通过ε可以修正轮胎滑移速度对计算轮胎力值的影响[14],ε取0.015;λ为轮胎与路面之间的滑动率;f(L)为Dugoff轮胎模型的修正系数;L为轮胎滑动造成的轮胎力非线性特征参数[15]。
Dugoff轮胎模型公式可以写成
(15)
(16)

1.3 非线性车辆动力学模型
在很多文献中滑移率和滑转率混为一谈,甚至滑转率视为滑移率,其实滑移率和滑转率是有所不同的,滑移率和滑转率统称为滑动率。滑移率是指车辆在制动行驶时,车轮的抱死程度,即λ=(ωre-v)/v;滑转率是指车辆在驱动行驶时,车轮的滑转程度,即λ=(ωre-v)/(ωre),其中,re为车轮的滚动半径;ω为车轮的转动角速度;v为车轮中心的纵向速度。故各轮的滑动率应统一为
(17)
式中,i、j为轮胎的位置,i为前轮或者后轮,j为左轮或者右轮。联立Dugoff轮胎力表达式(15)和(16),以及车轮转向时的运动学表达式(5)、式(6)、式(7),得到整车四轮转向时的非线性动力学微分方程
(18)
上述车辆微分方程在Matlab/Simulink中求解,如图3所示,采用的数值计算方法是Ode45。
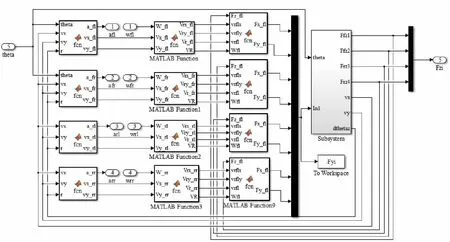
图3 基于Simulink的非线车辆模型数值计算
2 车辆状态与路面附着系数估计器设计
EKF算法建立在线性Kalman滤波方法上,其核心思想是,对一般的非线性系统,首先围绕滤波值将非线性函数f(*)和h(*)展开成Taylor 级数并略去二阶以上项,得到一个近似的非线性化模型,然后应用Kalman滤波完成对目标的滤波估计等处理。
EKF的优点是不必预先计算标称轨迹(过程噪声和观测噪声均为0时非线性方程的解),但它只能在滤波误差和预测误差较小时才能使用。EKF算法的求解过程包括:状态方程与观测方程的建立,模型的线性化,赋初值计算。卡尔曼滤波方法的核心为将非线性方程在其最优估计点做Taylor级数展开,取其一阶分量,使得方程线性化。
EKF滤波观测器选取纵向加速度、侧向加速度和横摆角速度3个参量作为观测量,构成了3个观测方程[16]。
扩展Kalman滤波算法流程如下:
(1)状态方程和测量方程。
状态方程
x(t)=f(x(t-Δt))
(19)
式中,f(x)=x;Δt为采样时间步长。
测量方程
y(t)=h(x(t),u(t),v(t))
(20)
车辆行驶状态矢量表示为
x(t)=[μfl,μfr,μrl,μrr]T
(21)
测量矢量表示为
(22)
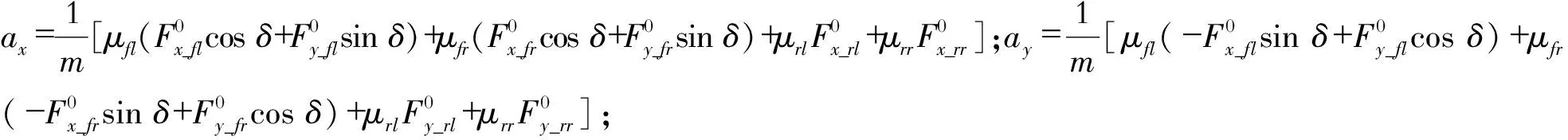
控制输入矢量表示为
u=[δ]
(23)
(2)模型线性化。H(t)表示函数h(x(t),u(t),v(t))对参数变量x求偏导之后的雅可比矩阵
(24)
(25)


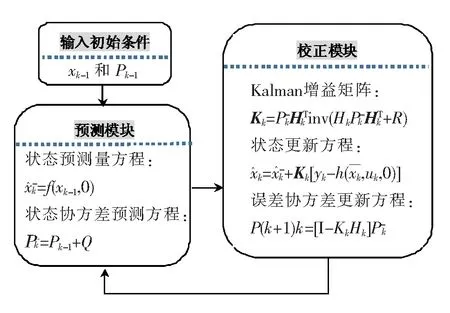
图4 EKF算法流程图
(3)给系统赋初值,进行递推运算,算法流程如图4所示。

对整车行驶状态和附着系数估计的完整算法流程为:
①在Simulink中搭建非线性车辆模型,计算任意工况下车辆的纵向速度、侧向速度、横摆角速度、质心侧偏角等反映行驶状态的时域响应,以及输出变量侧向加速度,控制输入转向转角和各车轮转速时域响应。
②将上述时域响应量代入到Dugoff轮胎模型中,求得8个重型车辆轮胎归一化的纵向力和侧向力。
③使用Matlab编程实现EKF控制算法,将归一化的轮胎力和转向轮转角等参数代入到EKF算法中,实时估计轮胎与路面的附着系数、行驶状态。
基于EKF的路面附着系数的算法原理如图5所示。

图5 基于EKF的路面附着系数的算法原理图
3 车辆状态与路面附着系数估计算法验证
由于篇幅所限,此处仅列出典型的双移线路线进行仿真试验,参考ISO—3888标准中的双移线工况[17-18],车辆行驶的轨迹如图6所示。试验车辆初始速度50 km/h,轮胎与路面的附着系数0.8,仿真时间8 s,采样时间间隔0.01 s。通过仿真,得到车轮前轮转向角和4个轮胎的转速,分别如图7和图8所示。

图6 ISO双移线工况的路线示意图(单位:m)

图7 前轮转向角位移
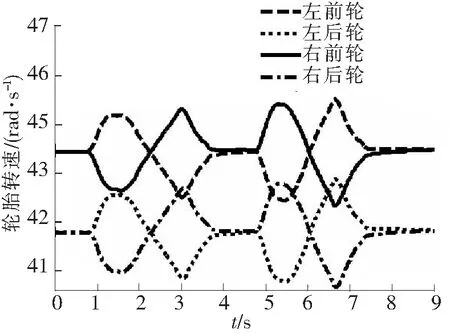
图8 轮胎转速
3.1 车辆行驶状态估计
通过双移线工况仿真结果分析,得到反映车辆行驶状态的质心纵向、侧向加速度和横摆角速度的时域响应,如图9、图10所示。对比图7可以确定,车辆的运动状态与转向角的输入激励的趋势是一致的,由此可以验证重型车辆侧偏的动力学模型是有效的。

图9 质心加速度

图10 横摆角速度
基于上述EKF算法,分别估计车辆的纵向速度、侧向速度、质心侧偏角、质心纵向加速度、质心侧向加速度、质心横摆角加速度,反映车辆行驶状态。对比分析EKF估计值与Simulink数值解,如图11~图16所示。
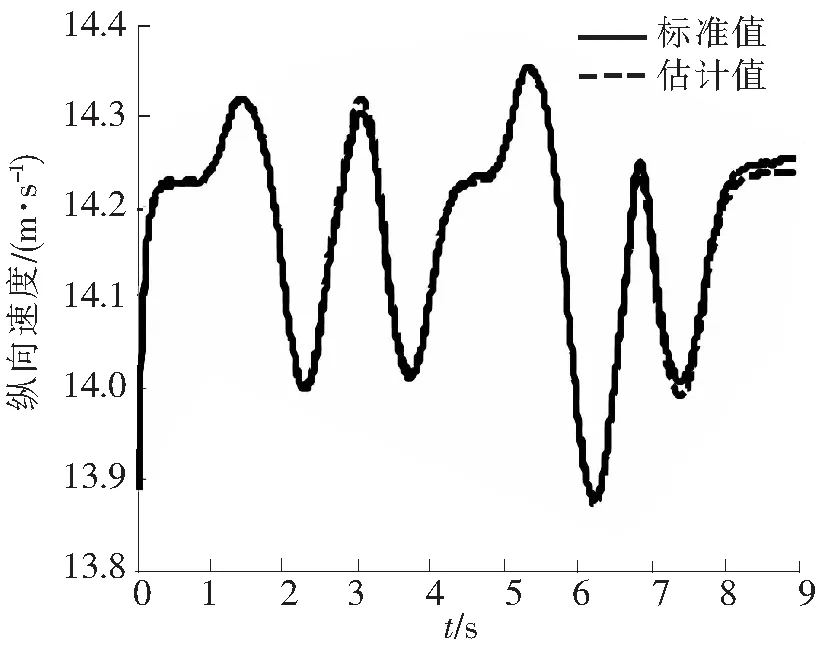
图11 纵向速度对比图

图12 侧向速度对比图

图13 质心侧偏角对比图

图14 质心横摆角加速度对比图

图15 质心纵向加速度对比图
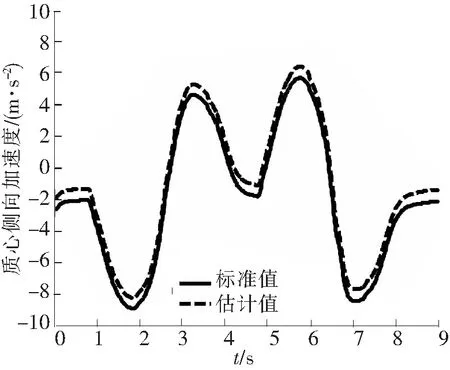
图16 质心侧向加速度对比图
估计值相对于Simulink数值解的均方根误差(RMSE)指标表达式如下
(26)

通过EKF估计值与Simulink数值解的对比曲线和其均方根误差,可以看出其精度和稳定性较好,趋势基本保持一致。其中,纵向速度、质心侧偏角和质心纵向加速度的EKF估计值精度较高,误差指标分别是0.014 0、0.017 1和0.002 14;侧向速度、质心横摆角加速度和质心侧向加速度的EKF估计值次之,误差指标分别是0.024 1、0.028 3和0.022 3。
3.2 车辆与路面附着系数估计
图17为车辆在同样的双移线工况下路面附着系数设定值分别为μ=0.8、μ=0.7、μ=0.6时与EKF估计值的对比图。

图17 轮胎附着系数对比图
可以看出,车辆在1 s后开始转向,由于轮胎与路面是动态接触,所以附着系数在系统设定值上下波动。该控制算法得到的汽车的状态和实际车辆状态基本吻合,控制算法获得的路面附着系数能够拟合出真实的路面附着系数。说明EKF控制算法在试验工况下能够有效地估计出汽车的状态和路面的附着系数。
4 结论
(1)基于Dugoff轮胎模型建立了非线性三自由度四轮整车模型,将轮胎力归一化代入,整个模型搭建过程在Simulink中实现,通过模拟双移线工况分析得到,车辆的运动轨迹和运动状态趋势吻合,初步验证了重型车辆侧偏动力学模型的合理性。
(2)从Simulink模型中获取各车轮转速和前轮轮胎转角,通过Matlab编程实现EKF算法,算法估算得到汽车状态参量。通过EFK估计值与Simulink数值解的对比曲线和其均方根误差,可以看出其精度和稳定性较好,趋势基本保持一致,且均方根误差指标最大值小于0.03;在路面附着系数分别为0.8、0.7、0.6的双移线工况下,将EKF算法估得的路面附着系数与设定值进行对比,来验证算法的有效性。充分证明了EKF算法具有较高的估计精度,同时也为后续的重型车辆稳定性控制奠定了基础。
