列车交叠动荷载对邻近基坑结构动力响应分析

(1.天津大学 建筑工程学院,天津 300072；2.天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072)

0 引言

近年来，随着城市轨道交通和高速铁路的大量修建，地铁运营所引起的周边环境振动响应问题越来越受到人们的关注，对地铁运营所引起的环境振动响应问题的研究具有重要意义，并有不少学者在相关方面进行研究[1]。对于列车动荷载，常采用现场实测或激振励函数法进行模拟[2-3]，或将列车荷载转换为静载进行分析[4-6]。通过这些荷载模拟方法的运用，广泛开展了列车动荷载对基坑结构动力响应的影响研究。张学民等[5]针对列车动载对偏压基坑围护结构的影响问题，建立了动力有限元模型，通过导入现场测试获得的列车激振荷载时程作用曲线，讨论了列车动载对偏压基坑围护结构的振动响应。马哲[7]采用人工数定法确定列车动荷载时程曲线，并通过FLAC 3D计算软件Drucker-Prager本构模型，对邻近地铁结构在列车荷载影响下的动力响应进行了分析。高广运等[8]通过推导动应力蠕变本构方程，并建立蠕变本构模型，利用数值模拟方法，讨论了列车移动荷载作用下的地基长期沉降。Meng Ma et al[9]通过开发地铁列车-轨道-隧道-土壤三维动态有限元模型，分析了2个重叠隧道的地铁列车振动对西安钟楼的影响，并根据模拟结果，研究了相应的隔振措施。Konstantinos Vogiatzis[10]对雅典地铁3号线新扩建段周边建筑物的地面噪声和振动水平进行了数学分析，并根据计算结果，对地面噪声高于允许值的建筑物提出了相应的减震措施。

然而，随着城市地下交通设施的大规模建设，交叠隧道已成为地铁隧道结构的重要布置形式。相较于一般情形，上下交叠隧道处地形条件更加复杂，交叠隧道处动荷载对周边基坑动力响应也更为复杂。但是，国内对于交叠隧道动荷载的振动响应研究主要集中在隧道结构及周边环境的单次响应上[11-12]，而对基坑开挖过程中列车交叠动荷载对基坑结构产生的影响少有研究，交叠隧道建设缺少完善的理论与技术支撑。因此，本文通过利用Abaqus有限元模拟软件，建立了交叠隧道-土体-围护结构三维动力有限元模型，对交叠隧道动荷载引起的周边土体及基坑围护结构的动力响应规律进行了研究，以期为相关的工程实践提供经验。

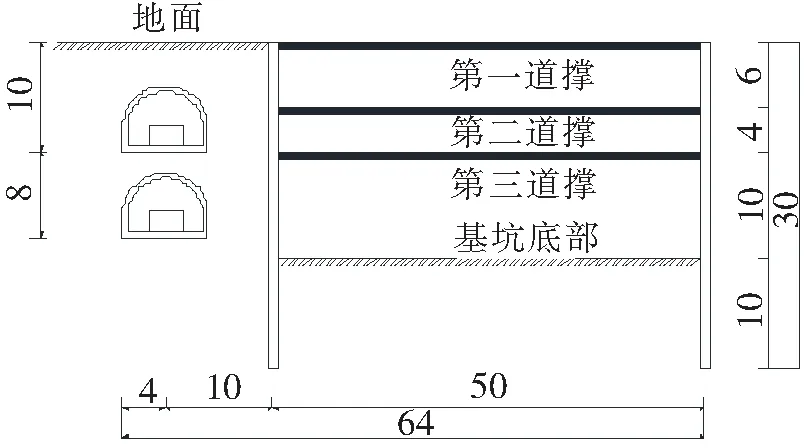
图1 基坑断面图(单位：m)

1 工程概况

某基坑开挖工程与周边地铁线路交叠隧道段相邻，交叠隧道与基坑工程的具体位置如图1所示。

该工程在开挖的过程中，不仅受到开挖卸载的影响，同时受到列车交叠动荷载的作用，直接影响到基坑工程的施工安全。为此，本课题以该工程实际为依托，讨论了列车交叠动荷载影响下的基坑围护结构变形与内力，以及周围土体的响应规律。

2 列车振动荷载的确定

列车在不平顺的轨道上行驶，竖向激振荷载可用一个激振力函数来模拟[13]，其表达式为

F*(t)=p0+p1sin(ω1t)+p2sin(ω2t)+p3sin(ω3t)

(1)

式中,p0为车轮静载，p1、p2、p3分别为①按行车平顺性、②按作用到线路上的动力附加荷载和③波形磨耗3种控制条件的振动荷载典型值。令列车簧下质量为M0，则相应的振动荷载幅值为

(2)

式中,ai(i=1，2，3)为典型矢高，i=1，2，3分别对应于控制条件①，②，③(以下同)；ω(i=1,2,3)为对应车速下不平顺振动波长的圆频率，故有

(3)

式中,v为列车的运行速度；Li(i=1，2，3)为典型波长。

考虑到列车轮对力在线路上的移动，叠加组合与钢轨、轮枕的分散传递因素[14]。将式(1)修正为

F(t)=k1k2F*(t)

(4)

式中,k1为相邻轮轨间的叠加系数；k2为轨枕间的分散系数。

k1、k2可根据车辆类型和轨道结构等条件选取，k1一般为1.2～1.7；k2一般为0.6～0.9，趋于结构安全性考虑，取最不利状况下的系数组合，即k1=1.7,k2=0.9。其他参数的具体取值见文献[1]，分别进行60 km/h、80 km/h、120 km/h的列车荷载计算，其中60 km/h列车的振动荷载如下

(5)

3 列车振动响应数值分析

3.1 动力计算模型的建立

为客观反应基坑结构对交叠动荷载的动力响应特征，拟建立三维动力有限元差分模型。为减少边界条件的影响以及考虑到计算机的计算能力，最终选择模型尺寸为x方向(横向)180 m，z方向(纵向)120 m，y方向(竖向)70 m。其中,土体、隧道围护结构分别采用实体单元，基坑围护结构采用壳单元，基坑支撑采用梁单元模拟。模型四周设置法向约束，底部为固定边界。三维网格模型及材料属性如图2所示。

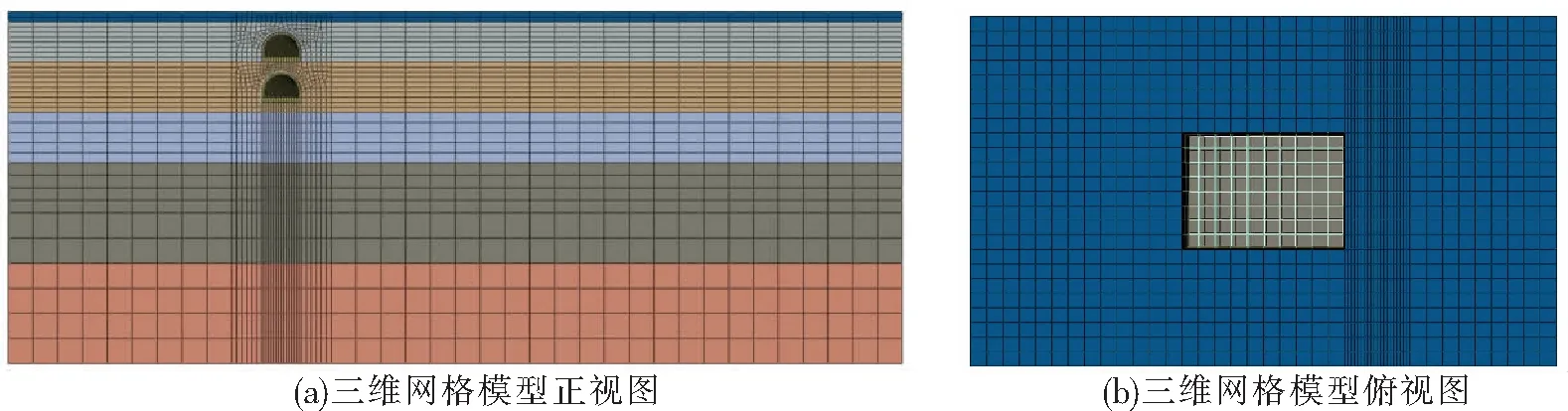
图2 三维网格模型

3.2 动力分析步骤与计算工况

限于问题的复杂性，动力分析中列车动载的长期累积效应和疲劳效应对围护结构变形和内力累计损伤的影响未进行考虑，而是通过将动力荷载作用产生的应力场导入余下分析步，从而考虑列车动载对基坑施工的影响[6]，具体施工步如下：

①重力作用下，计算地应力平衡。

②施做连续墙。

③施加动力荷载，进行动力分析。

④基坑开挖2 m,施做第一道撑。

⑤基坑开挖8 m，施做第二道撑。

⑥基坑开挖15 m，施做第三道撑。

⑦基坑开挖至基坑底。

分别建立列车时速为60 km/h,80 km/h，120 km/h列车交叠动载激励作用下的计算分析，并与只考虑列车静载以及不考虑列车荷载的分析工况进行对比，从而得出交叠动载对地表沉降及基坑内力与变形的影响规律。为了讨论交叠动载与单层动载作用规律的差异，建立120 km/h时速下，上层列车动载单独作用以及下层列车动载单独作用的工况，通过与交叠动载作用工况的对比，从而得出交叠动载与单层动载作用规律的差异。

3.3 动力计算参数的选取

模型的材料物理参数见表1。

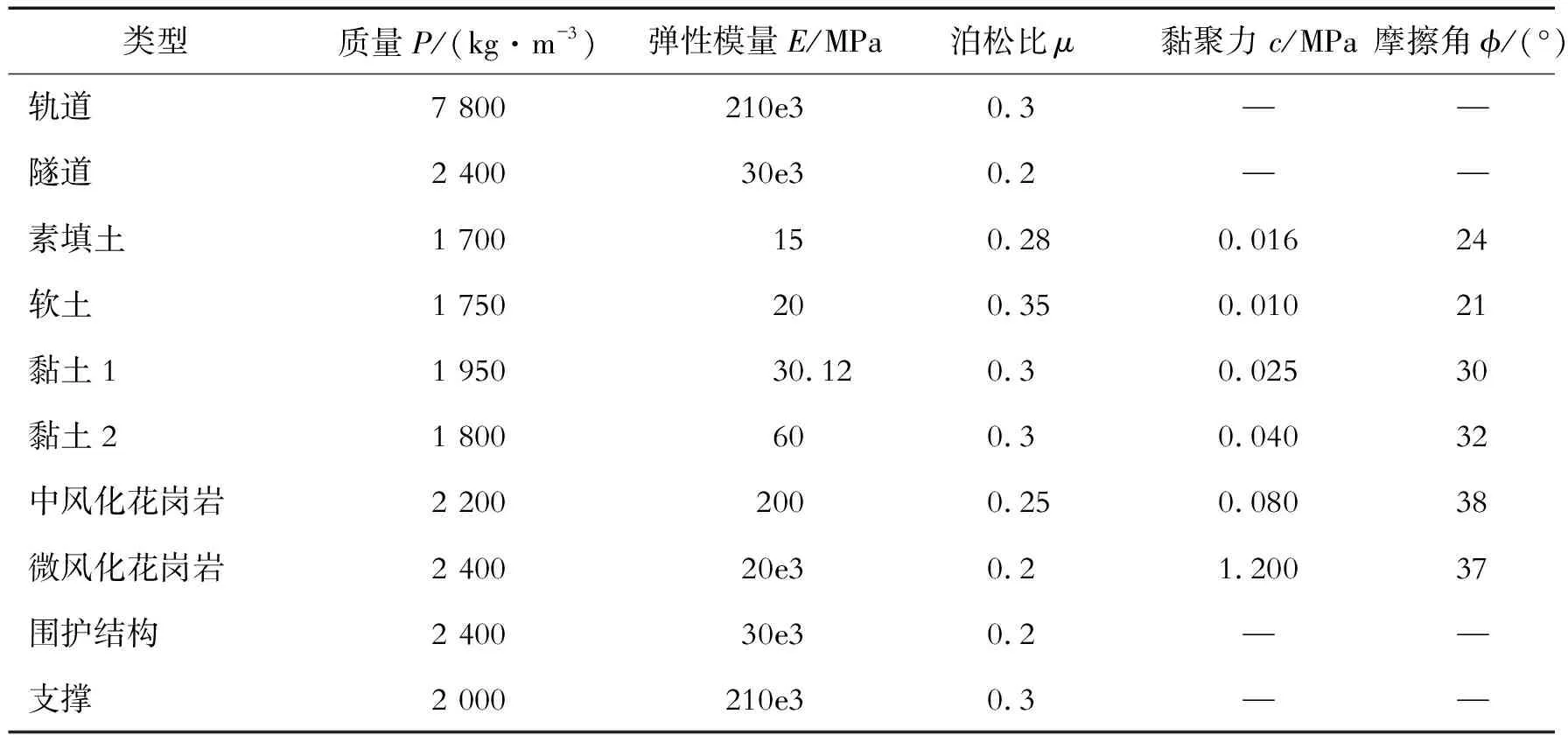
表1 动力模型土层及结构物理参数值

为了考虑振动过程中的能量耗散特性，在模型中采用Rayleigh阻尼，其表达式为[15]为

[C]=α[M]+β[K]

(6)

式中,[C]为阻尼矩阵；[M]为质量矩阵；[K]为刚度矩阵；α为质量相关阻尼系数；β为刚度相关阻尼系数。Rayleigh阻尼的系数α和β与体系的阻尼比和固有频率有关[1]，有

(7)

式中,ω0为系统的基频；ε0为相应振型的阻尼比。

由于在讨论体系的固有特性时，阻尼对固有频率以及固有模态的影响比较小，因此可以按无阻尼系统进行模态分析，提取体系的固有频率，求取阻尼系数[16]。

3.4 动力模拟的计算结果及分析

通过数值计算，获得列车动载作用下基坑两侧地层及围护结构的变形和内力响应分布曲线，在(1)-(4)小节中，为交叠列车动载作用的5种工况下结果分析对比。在第(5)节中，为列车时速为120 km/h时，上层列车荷载单独作用、下层荷载单独作用、交叠列车荷载作用的模拟结果，与不考虑列车荷载工况模拟结果差值的对比分析。

3.4.1 基坑连续墙外侧土层沉降变化规律

以隧道方向的基坑两侧围护结构中心处为基准点，向外延伸绘制地表沉降图，如图3所示。

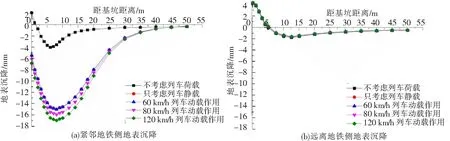
图3 5种工况地表沉降曲线对比

图3是5种工况下基坑开挖至基坑底后相应的最终地表沉降曲线。由图可知，考虑地铁荷载后，远离铁路侧的地表沉降稍有变小，但影响较小，不同工况下的沉降曲线基本重合。而紧邻铁路侧的地表沉降差异显著，不考虑列车荷载工况地表沉降量最小，考虑列车荷载后沉降明显增大。

对于近地铁侧，60 km/h列车动载作用与列车静载作用的结果接近，差值在3%以内，这表明低速行驶的列车，可以只考虑列车静载的作用。而随着列车速度的增加，地表沉降量也逐渐增大，列车时速为120 km/h时，地表最大沉降达16.98 mm，相比等效静载的计算下，增大13.28%。从力学机理而言，随着列车时速的增加，由列车振动所引起的附加动载部分也逐渐增加，所引起的振动响应也逐渐增大。对于高速行驶的列车，在讨论地表沉降之时，不能只考虑列车静载的作用，还需考虑列车振动引起的附加荷载的影响。

3.4.2 连续墙水平位移变化规律

以隧道方向基坑两侧的中心处为基准点，向下延伸绘制基坑围护结构变形与内力图，如图4、图5所示。

图4 5种工况下连续墙水平位移对比

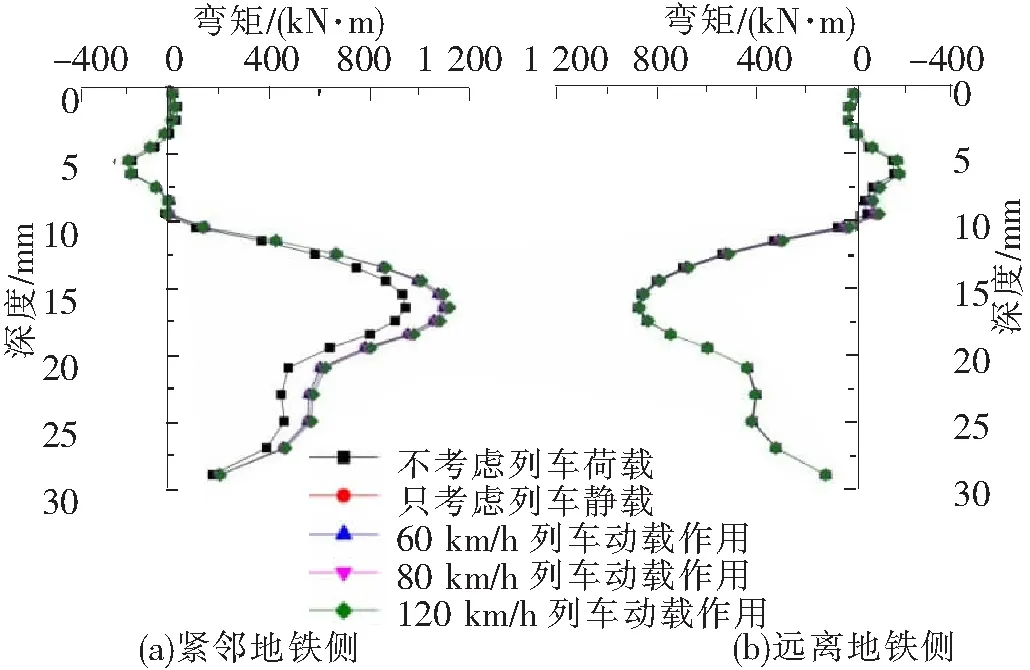
图5 5种工况下连续墙弯矩对比图

随着列车时速增加，紧邻铁路侧墙体水平位移增大，而远离铁路侧墙体水平位移减小，但连续墙水平位移的变化幅度受列车时速的影响不大。对于近地铁侧，120 km/h列车荷载工况与列车等效静载工况相比，紧邻铁路侧墙体水平位移仅增大1.94%， 120 km/h列车荷载工况与不考虑列车荷载工况相比，紧邻铁路侧墙体最大水平位移由20.84 mm增大为24.23 mm，增大16.27%。从力学机理而言，围护结构自身的抗侧刚度较大，抵抗周边荷载的能力较强。而列车荷载相当于一个较大的偏压荷载，随着列车时速的增加，其所产生的附加动载虽然不断增加，但总体而言，仍是静载处主要控制作用。因此，在讨论列车荷载对墙体水平位移的影响时，列车荷载的作用不能忽略，而在列车荷载的作用中，又以列车静载起主要作用。

3.4.3 连续墙弯矩变化规律

5种工况计算结果(如图5)表明，随着列车时速的增加，紧邻铁路侧连续墙的弯矩增大，而远离铁路侧连续墙的弯矩稍有减小。对于近地铁侧，基坑开挖至基坑底时，考虑列车动载工况与只考虑列车静载工况相比，计算结果比较接近，列车时速120 km/h工况与只考虑列车静载工况相比，连续墙最大弯矩增加2.23%。而120 km/h工况与不考虑列车荷载工况相比，墙体最大弯矩由942.084 kN·m增加到1 118.590 kN·m，增值为18.74%。这表明，在讨论列车荷载对墙体弯矩的影响时，不能忽略列车荷载的作用，而在列车荷载作用中，以列车静载起主要作用。

3.4.4 内撑轴力的变化规律

对比表2的数据可知，对于第一道撑的轴力，列车荷载的影响很小，增幅仅不到1%，且列车静载起主要作用。对于第二道撑的轴力，列车静载部分起增大作用，而列车动载部分起减弱作用，时速120 km/h相比列车静载作用，第二道撑的轴力减少28 kN,减幅为2%。对于第三道撑的轴力，列车静载与列车动载均起增大作用，且列车动载起主要作用，相比不考虑列车荷载工况，120 km/h列车动载工况作用下，轴力增大3.05%。总的来说，列车荷载对于内撑轴力的影响较小。

表2 5种工况下计算的支撑轴力 kN

3.4.5 与单层列车动载作用的对比

为了讨论单层列车动载与交叠列车动载动力响应的影响差异，利用列车时速为120 km/h时，上层列车荷载单独作用、下层荷载单独作用、交叠列车荷载作用的模拟结果，与不考虑列车荷载工况模拟结果的差值进行对比分析，结果如图6、图7所示。

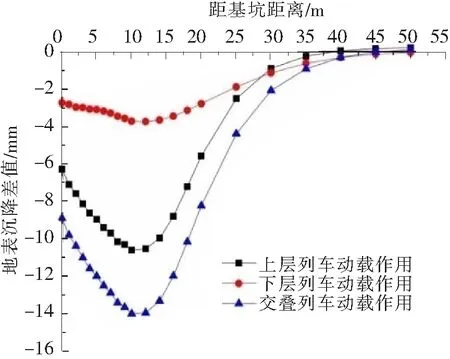
图6 地表沉降差值曲线图

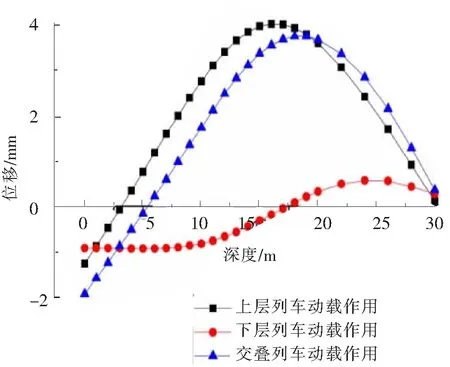
图7 连续墙侧移差值曲线图

由图6可知，对于地表沉降，无论是单层列车动载作用又或是交叠列车动载，均起加大的作用，而其影响值的最大值约在距基坑10 m远处(即隧道中心线的位置)。列车荷载对于地表沉降的影响范围约为以隧道为中心的30 m区间内，在这个区间之外的影响，可以忽略不计。从3种工况影响数值大小上来看，总的来讲，交叠动载的影响>上层动载的影响>下层动载的影响，这说明在交叠列车动载对于地表沉降的共同作用中，以上层列车动载的影响起主要控制作用。

与地表沉降不同，列车动载对于连续墙侧移的影响则较为复杂，总的来讲，是先减小后增大的趋势。从图7来看，在单层列车荷载作用时，对于高程高于隧道荷载作用位置的连续墙侧移往往有减小作用，而对于高程低于隧道荷载作用位置的连续墙侧移则有增大作用，两者的分界处约在列车荷载作用处上下2 m内。交叠列车动载的作用规律，与起主要控制作用的上层列车动载的规律接近，但减小与加剧的分界处不明朗，需要结合具体工程情况具体分析。值得注意的是，在本工程实际下，由于下部隧道位置较深，最低处位于地底18 m的位置，因此下层列车荷载对于上部的围护墙侧移起衰减作用，这也导致出现了上层列车荷载单独作用下连续墙侧移大于交叠列车动载作用的情况。对于本工程实际，在上层动载单独作用时，连续墙的最大侧移为25.17 mm，比交叠动载作用时多出2%，比不考虑列车荷载作用时高出19%。因此，遇到上下交叠动载作用的工程实际，在考虑列车动载对围护结构的影响时，不应只考虑交叠动载的作用，还需要与单层列车动载单独作用的情况进行对比。

4 结论

联系某基坑工程的工程实际，对列车交叠动荷载影响下的基坑围护结构变形与内力，以及周围土体的响应规律进行了三维数值分析，得到了以下相关结论：

(1)列车荷载作用对近地铁侧地表沉降影响较大，对远地铁地表沉降影响较小。列车动载作用使得邻近地铁侧的地表沉降加大，且随着列车时速的增大地表沉降也逐渐增大。当列车时速低于60 km/h时，考虑列车动载与只考虑列车静载作用的结果接近，可以用列车静载等效考虑。对于高速行驶的列车，必须考虑列车动载的作用，而不能只考虑列车静载的作用。

(2)列车荷载作用对近地铁侧基坑围护结构的弯矩和变形影响较大，对远地铁侧基坑围护结构的弯矩和变形影响较小。列车荷载对基坑围护结构弯矩和变形的影响中，以列车静载起主要作用，而列车动载的影响较小，在设计中可以只考虑列车静载的作用。列车荷载对支撑轴力的影响较小，在5%以内，在设计中可以忽略列车荷载对支撑轴力的影响。

(3)交叠列车动载对地表沉降的影响规律与单层列车动载影响规律相似，均是增大作用，且最大影响位置均处在隧道中心处，而向两侧不断减弱，影响范围大概是30 m内。交叠列车动载对与地表沉降的影响大于单层列车动载的影响，且以上层列车动载的作用起主导作用。

(4)交叠列车动载对基坑围护结构侧移的影响规律较为复杂，总的来说是先减小后增大的趋势。单层列车动载作用下，两者的分界处较为明确，约在荷载作用处上下2 m内，交叠列车动载作用时则不明确。由于下层列车动载对于基坑围护结构的减小作用，可能会出现交叠列车动载对围护结构侧移的影响小于上部列车动载单独作用下的情况，在实际工程中，必须针对具体问题进行具体分析。