小型高温加热装置内部传热特性的模拟计算

姜 琦 余南阳

小型高温加热装置内部传热特性的模拟计算

姜 琦 余南阳

（西南交通大学机械工程学院 成都 610031）

以用于小型金属试样材料高温动态力学性能试验中的加热装置为研究对象，对与实验室现有小型压入测试试验机相匹配的加热装置进行传热特性研究。运用数值模拟方法得到并分析动态传热过程，以试样内能增加量一致时所需时间为衡量指标，讨论了总输入功率一定时，腔体几何参数对试样升温效率的影响。研究表明：随着传热过程进行，腔体对流热损失比重逐渐减小，辐射热损失比重逐渐上升并最终占据主导地位；在设计与优化加热装置腔体结构时，适当增大开口比有利于加快试样升温速度；开口比一定时适当增加高宽比或改变腔体形状也对改善试样升温效率有利。

高温加热装置；非接触式加热；数值模拟；工程应用

0 引言

材料动态力学性能实验在指导实际工程应用中具有重要作用，当前工程材料的工作环境越来越苛刻，高温条件下材料的动态力学性能是人们非常关心的一个问题[1]。材料热力学性能实验中的加热装置要求具有较快的升温速度、较短的处理周期和较高的温度控制精度[2]。加热方式和新型加热材料的研究开发已经成为材料科学和能源开发领域的研究热点[3]。因此，需要对应用于此类试验的加热装置进行传热特性研究，而数值计算的方法具有成本较低和能模拟较复杂过程的优点，从而能减少成本昂贵的实验工作量[4]。

本文针对实验室现有小型金属材料压入试验机的规格选取合适热源并设计相应的高温加热装置，然后运用Fluent流体仿真软件进行瞬态数值模拟，得到加热装置动态热传递情况并分析了不同腔体几何参数对试样升温情况的影响。

1 高温加热装置简介

本文所研究的加热装置是为材料高温动态力学性能实验服务，采用非接触式加热方式[5]，在试样上升到指定温度后需将压头压入加热腔内给试样施加一定压力，加热装置截面示意图见图1。选用氮化硅陶瓷加热器作为高温发热元件，它是以陶瓷为基体，以钨丝为发热源，钨丝埋在陶瓷基体中，通过热压烧结的方法形成一体，再磨削加工，焊接引线，制成的发热元件，具有热惯性小、升温速度快等优点，在空气中加热到1000℃以上时，急剧冷却再急剧加热也不会碎裂，可以满足试验的温度需求。加热腔顶部设计为开口形式，已有大量关于开口空腔热特性的研究表明[6,7]，开口大小和内壁温度对空腔辐射热损失起着决定性作用，因此腔体开口需在满足压头规格下尽量减小。考虑到热源温度较高，采用保温效果较好的硅酸铝陶瓷保温棉作为保温层材料。在总输入热量一定时，腔体的几何参数会对试样单位时间内得到的热量即升温速度产生影响，因此本文将从开口比、高宽比、腔体形状等方面进行讨论。

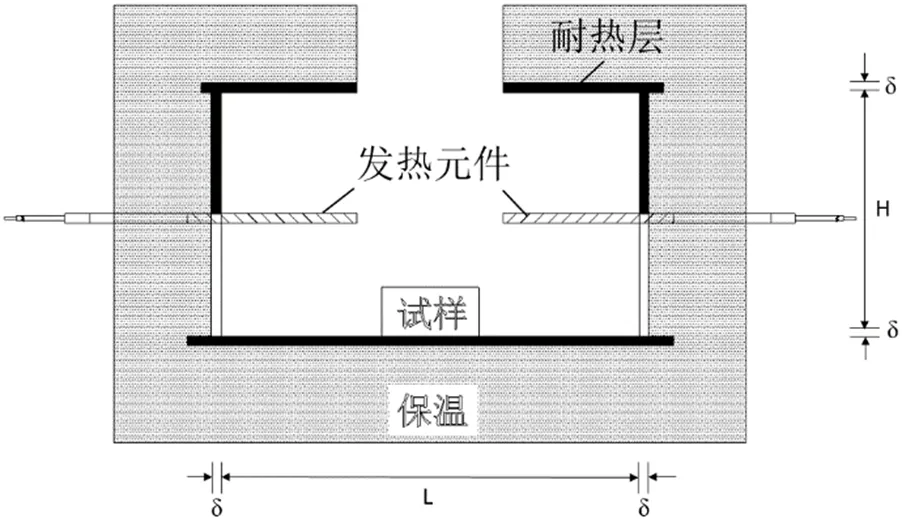
图1 加热装置截面示意图

2 数理模型及求解方法

2.1 物理模型

对图1所示的加热装置进行模拟计算，模拟所用具体尺寸为：和分别表示腔体高度和宽度；腔体开口尺寸为30×30mm；氮化硅陶瓷加热器的尺寸为30mm×12mm×2mm，单个发热元件额定功率为300W；耐热层厚度为10mm；保温层厚度设为50mm；待测金属试样的材料为16Mn，尺寸为20mm×20mm×10mm。

2.2 数学模型与求解方法

本文采用Fluent软件对模型进行三维瞬态数值模拟。将氮化硅陶瓷加热器设为体热源，产热率为3.57×107W/m3；加热腔内壁面和试样表面为耦合边界；保温层外表面为对流传热边界，其对流换热系数利用流体相似理论确定，不考虑保温层表面向周围空间的辐射散热；根据文献[8,9]中的处理方式，计算区域与加热装置尺寸大小一致，腔体开口设为压力入口边界。

表1 各表面发射率

加热装置内部传热过程是一个伴随有流动与换热的动态变化过程，由于发热元件温度较高（900℃以上），属于高温传热范畴，因此辐射传热不可忽略。加热腔内部辐射属于多表面辐射换热，所有参与辐射的表面均为漫灰表面。表面发射率设置见表1。计算采用Discrete Ordinates（DO）辐射模型，辐射传热基于灰体假设，同时开启能量方程。空气视为不可压缩流体，由于腔内物体与外界环境的温度差异较大，加热腔内部的空气物性参数会发生较大变化，Boussinesq假设将不再适用，因此在大温差情况下，空气拟采用变物性处理[10]。空气流动属于牛顿流体的湍流流动，采用RNG-湍流模型。控制方程描述如下：

连续性方程：

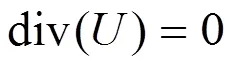
动量方程：

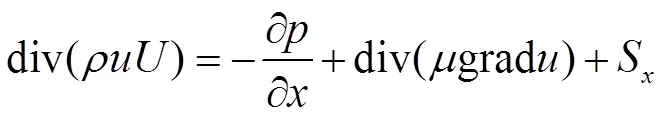
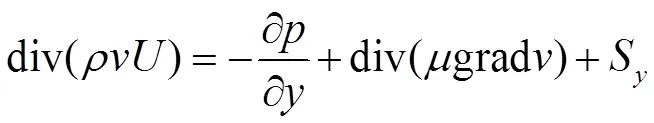
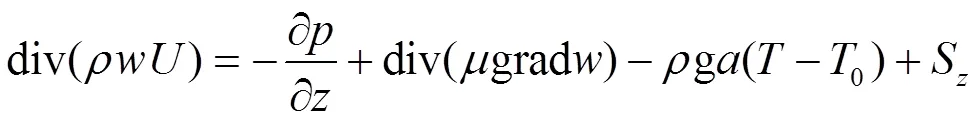
能量方程：

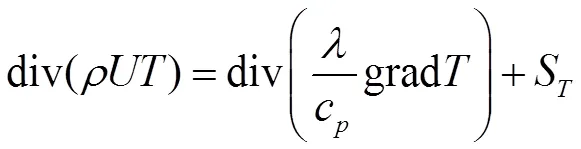
本文采用六面体非结构化网格，通过试算对网格和时间步长进行无关性验证后，选定网格尺寸为1×1×1，时间步长为0.5s。

2.3 计算模型验证

将本文选用的数值计算模型对文献[11]中的实验工况进行计算，结果对比如表2所示，其中，下标“”和“”分别代表腔体侧面和底面温度，“exp”为文献中的实验数据，“num”为计算数据。由表格可知，三种工况下，稳态计算结果与实验结果基本吻合，最大偏差为10.6%，说明本文所用模型较为可靠。

表2 本文模拟表面温度与文献[11]对比

3 模拟结果与分析

3.1 耦合传热瞬态过程分析

图4和图5为瞬态过程发热元件、试样、内壁的温度及表面热流密度随时间的变化曲线，其中，离开壁面的热流为正值[12]。对试样而言，其表面热流密度的变化趋势与其同热源和壁面温度之差的变化都是先增加后减小直至平稳的过程。试样升温曲线斜率较大时对应其表面吸收的热量不断增加，此时试样表面辐射热流占总热流的60%以上且之后的占比不断增加，说明腔内辐射传热对试样升温情况影响较大，提升试样升温效率可从改善腔体辐射传热入手，而影响固体表面间辐射换热的主要因素[13]包括固体表面的辐射物性、表面的几何特征（大小与形状）和相对位置、表面温度。

图6为加热装置三种传热热损失及试样得热量占热源输入总热量的比例随时间变化曲线，在初始时间内，腔内温度较低，通过开口的对流热损失占主导地位，随着传热过程进行，对流散热占比随之减小，辐射热损失比重不断增加，这是由于热源温度持续上升，加热腔内外温差增大，导致辐射换热增强。保温层隔热效果优良，因此导热损失随时间变化幅度较小。650s后辐射热损失强于对流热损失，且三种传热量占比趋于稳定，与各表面温度变化趋势一致。

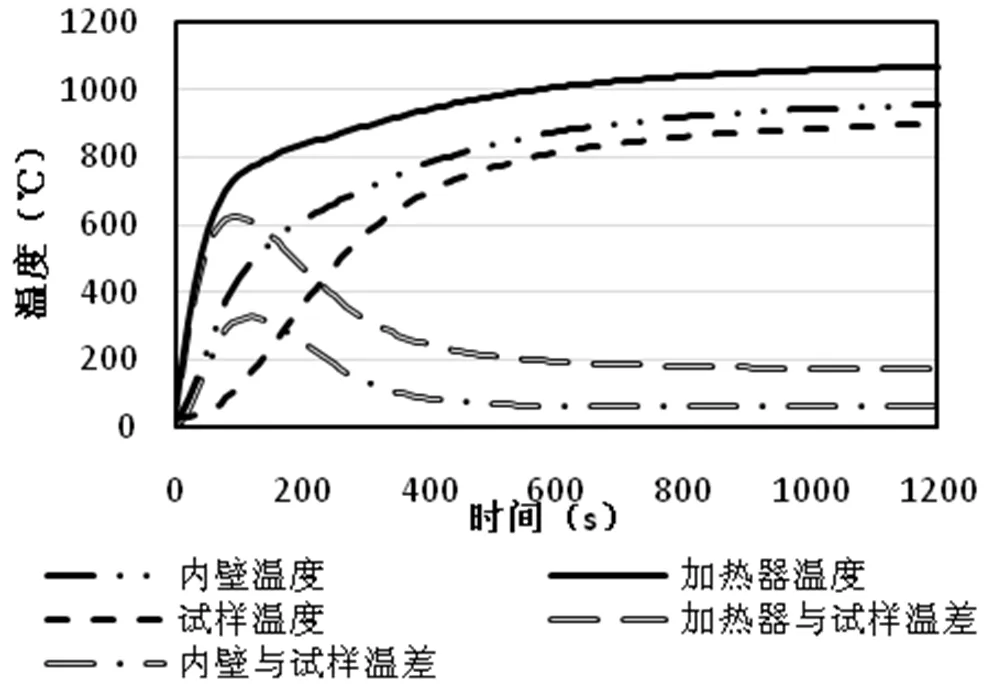
图4 温度变化曲线

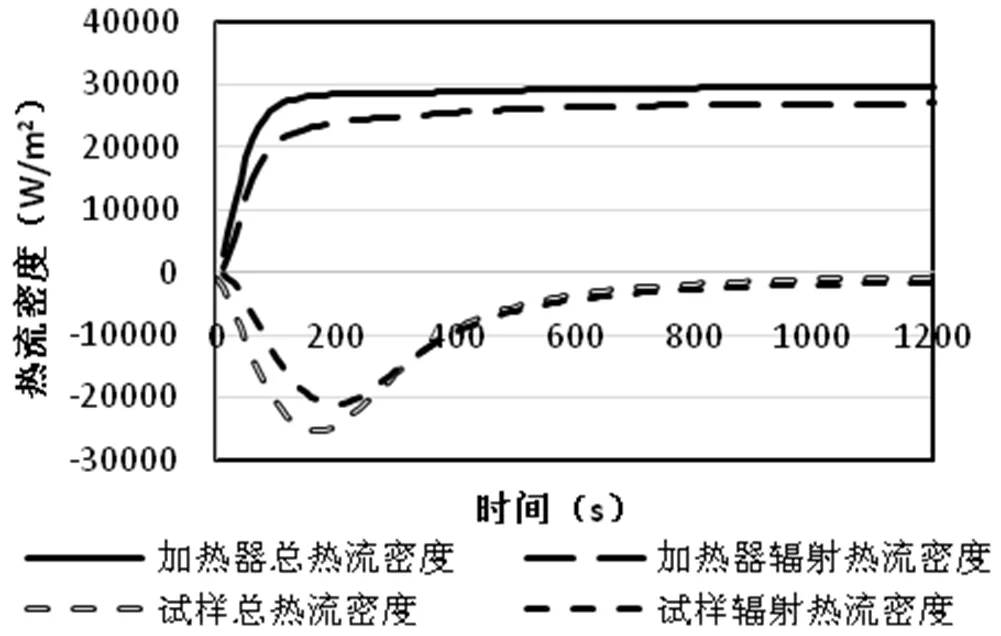
图5 热流密度变化曲线

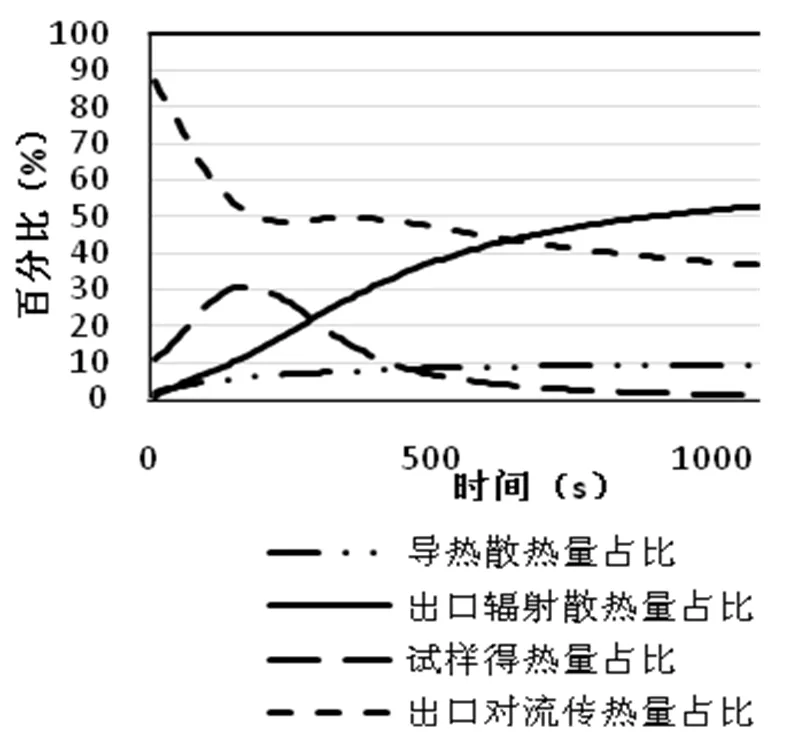
图6 腔体热损失及试样得热量占比变化曲线

3.2 腔体开口比的影响

腔体的内壁面可视为散热面，会对腔体热性能产生影响。本小节将探讨腔体开口面积A一定，通过改变内表面积A来改变腔体开口比A/A时对试样升温效率的影响。腔体编号及具体规格见表2，腔体1#～6#的开口比依次增加，其中，腔体1#～4#高宽比依次减小，腔体4#～6#腔体高宽比依次增加。计算结果如图7所示。

当试样达到800℃时，在本节计算范围内，无论高宽比如何，试样的升温效率随开口比增加而提高。使用2#～6#腔体时试样升温所需时间依次比1#腔体缩短了7.9%、15.3%、22.9%、35.9%和53%。进一步对比方腔2#和6#以及方腔3#和5#，前一组高宽比约为0.4，后一组高宽比约为0.3，在高宽比相同的情况下，增大开口比对于试样升温速度影响显著。在发热元件输入功率一定时，腔体内表面积减小，热源在单位时间内传递给腔内物体单位面积上的热量增加，试样内能增加速度也随之加快。

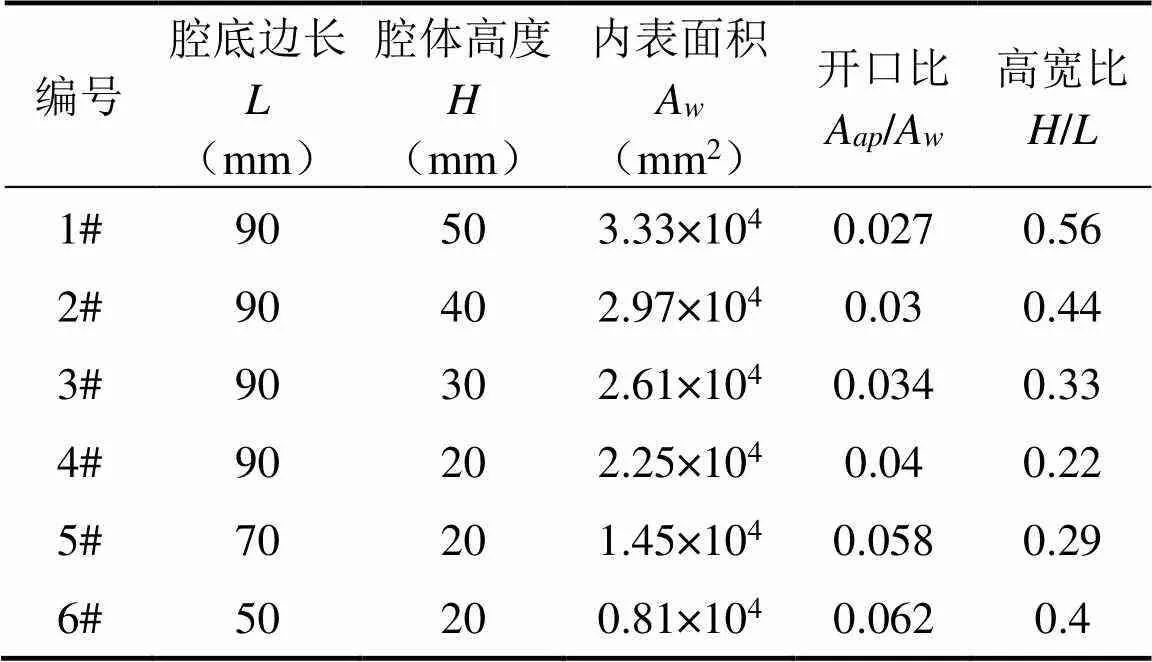
表2 腔体规格

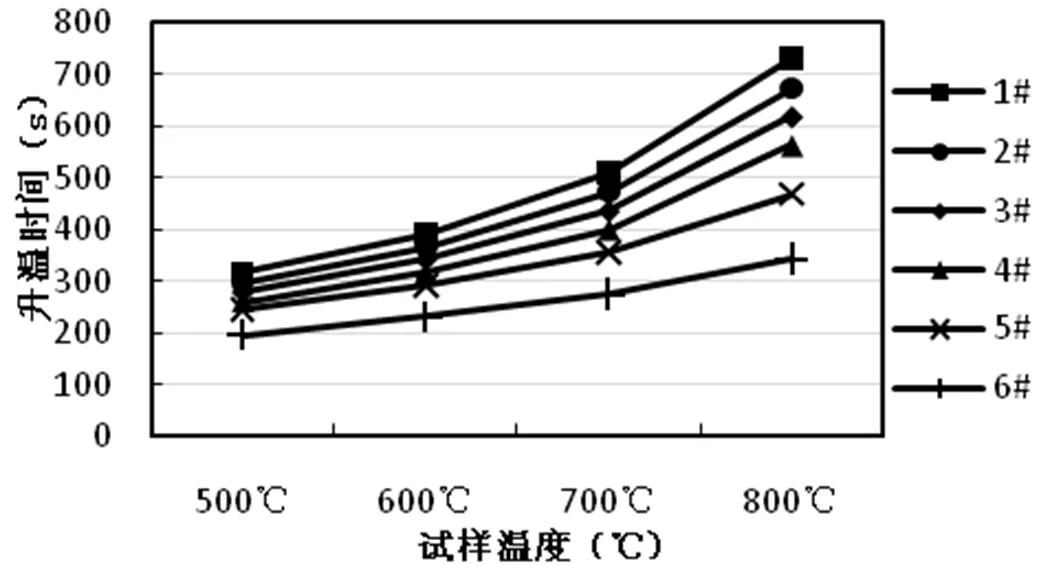
图7 温度变化曲线

3.3 腔体高宽比及形状的影响

本小节将讨论腔体开口比A/A不变的情况下，改变高宽比或腔体形状对试样升温过程的影响。取A/A=0.04，具体尺寸见表3，腔体4#～11#的高宽比依次增加，9#的高宽比约为1，12#为棱台型腔体，腔体侧壁面与底面夹角为75°。试样升温曲线见图8。

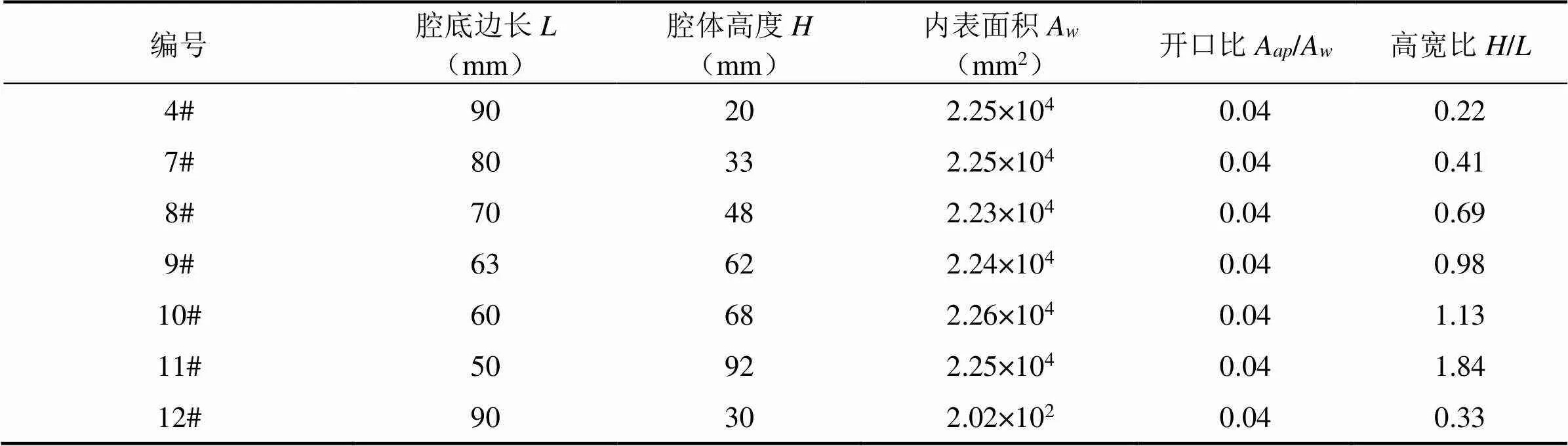
表3 腔体规格

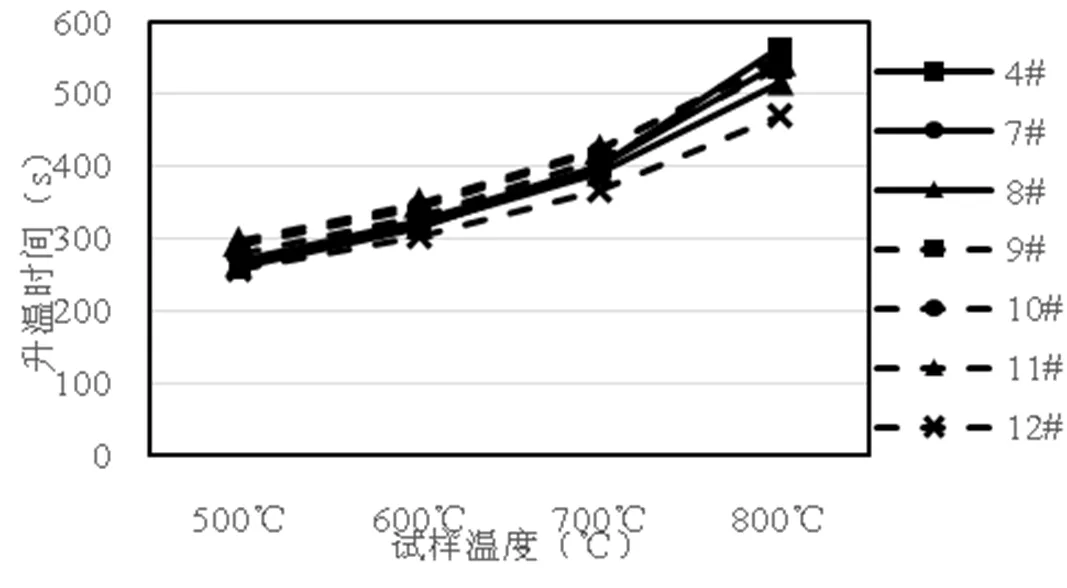
图8 温度变化曲线

由计算可知，在腔体开口比A/A相同即腔体内表面积一定时，改变方型腔体的高宽比对试样升温过程影响较小，当试样达到800℃时，7#～11#腔体中的升温时间依次比4#腔体缩短了3.6%、8.3%、5%、2.1%和2.8%，8#腔体表现更优，＞1以后改善效果不再显著，且根据实际情况，方型腔体的高宽比最好控制为不大于1。继续比较12#腔体的效果，试样内能增加量一致时，所需时间比4#腔体减少了16.5%。可见在腔体开口比一定时，通过减小腔体侧面与底面夹角等方式改变腔体形状可有效提高试样升温效率。

4 结论

通过对加热装置的传热过程进行模拟计算，可以得到以下结论：

（1）在试样升温过程中，辐射传热量可占其表面吸收总热量的60%以上，因此提升试样升温效率可从改善腔体内部表面间的辐射换热入手。

（2）当腔体开口面积不变时，通过增大腔体开口比及减小内表面积可以有效提高试样的升温效率。

（3）当腔体内表面积一定时，腔体高宽比的变化对于试样升温速度的影响较小，但通过减小腔体侧面与底面夹角等方式来改变腔体形状可进一步提升试样的升温效率。

[1] 邓志方.高温SHPB实验中的界面热传导特性及其影响[D].绵阳:中国工程物理研究院,2006.

[2] 蒋玉雷.快速热处理设备温度场控制技术研究[D].北京:北方工业大学,2013.

[3] 张颖异,李运刚,张快,等.高温电热材料的研究发展[J].热加工工艺,2011,40(18):40-43,47.

[4] 陶文铨.数值传热学(第2版)[M].西安:西安交通大学出版社,2001.

[5] 徐智.高精度加热平台的研制[D].武汉:华中科技大学,2009.

[6] 徐连辉.一侧开口式圆柱形腔体热损失特性的实验研究[D].重庆:重庆大学,2012.

[7] 郭凤华.基于壁面均匀热流的部分开口式圆柱形腔体耦合热损失特性的数值模拟[D].重庆:重庆大学,2013.

[8] Kambiz Vafai, Javad Ettefagh. Thermal and fluid flow instabilities in buoyancy-driven flows in open ended cavities[J]. International Journal of Heat and Mass Transfer, 1990,33(10):2311-2328.

[9] E Bilgen, H Oztop. Natural convection heat transfer in partially open inclined square cavities[J]. International Journal of Heat and Mass Transfer, 2005,48(8):1470- 1479.

[10] Sendhil Kumar Natarajan, K S Reddy, Tapas Kumar Mallick. Heat loss characteristics of trapezoidal cavity receiver for solar linear concentrating system[J]. Applied Energy, 2012,93:523-531.

[11] Zu-Guo Shen, Shuang-Ying Wu, Lan Xiao, et al. Experimental and numerical investigations of combined free convection and radiation heat transfer in an upward-facing cylindrical cavity[J]. International Journal of Thermal Sciences, 2015,89: 314-326.

[12] Fluent Inc. Fluent user’s guide[M]. 2006.

[13] 余其铮.辐射换热原理[M].哈尔滨:哈尔滨工业大学出版社,2000.

Numerical Simulation of Heat transfer Characteristics in a High Temperature Heating Device for Experiment

Jiang Qi Yu Nanyang

( School of Mechanical Engineering, Southwest Jiaotong University, Chengdu, 610031 )

The research object is the high temperature heating device used in the dynamic mechanical properties of materials under certain high temperature conditions in this paper. The device was designed according to the small-sized press-in material testing machine developed by our laboratory. Taking the time required for the increase of internal energy of the sample as a measure, the effect of cavity geometry on the heating efficiency of the sample is discussed when the total input power is constant based on numerical simulation. The results show that as the heat transfer process proceeds, the proportion of convective heat loss in the cavity gradually decreases, and the proportion of radiant heat loss gradually increases and eventually dominates; When designing and optimizing the cavity structure of the heating device, appropriately increasing the opening ratio is beneficial to speed up the heating rate of the sample; Appropriate increase of the aspect ratio or changing the shape of the cavity when the opening ratio is constant is also beneficial to improve the heating efficiency of the sample.

high temperature heating device; non-contact heating; numerical simulation; engineering applications

TK32

A

1671-6612（2020）01-122-05

姜 琦（1993-），女，在读硕士研究生，E-mail：jqecho007@163.com

余南阳（1961-），男，博士，博士生导师，E-mail：rhinos@126.com

2019-11-09