基于阻塞滤波器的抗主瓣干扰方法

(国防科技大学电子对抗学院电子对抗信息处理军队重点实验室， 安徽合肥 230037)

0 引言

为了能够在复杂电磁环境下依然能获得较好的探测目标能力，要求雷达具有较好的抗干扰能力。当干扰从雷达的副瓣进入雷达天线时，采用旁瓣对消、自适应波束形成、旁瓣匿影、旁瓣对消等方法[1-2]可以获得较好的抗干扰效果。但是当干扰从天线的主瓣进入时，这些方法几乎完全失效。

随着研究的深入，近年来提出了很多抗主瓣干扰方法。尹洪伟等提出了基于时频解耦的盲源分离算法，来解决单通道欺骗干扰，通过将混合时频线性调频信号转化成两个差额信号，通过二次拉伸变换构造出虚拟信道[3]，从而将欠定问题转化为适定的莽原分离算法。周青松等提出了利用盲源分离算法对信号进行分离，然后利用分数阶傅里叶变换(FRFT)对分离的信号进行处理[4]，但是这种方法破坏了信号的相位信息，对后期信号的参数估计带来了困难。文才等利用天线的极化特性，研究了利用信号的极化特性滤除主瓣干扰的方法[5]，但是这种方法的抗干扰性能有限。苏保伟等提出了基于阻塞矩阵预处理的抗主瓣干扰方法研究，但此方法需要准确知道主瓣干扰信号的波达角(Direction of Arrival, DOA)，而对于干扰信号的估计需要利用MUSIC等算法，算法的复杂度较高[6]。Yu等研究了基于四通道主瓣干扰抑制算法，该方法与传统的单脉冲测角相比多构造出一个双差波束，形成特殊的旁瓣对消结构，从而将主瓣干扰抑制掉，但是该系统增加了系统的硬件复杂度且只能对消掉一个主瓣干扰信号[7]。目前国内外对于利用对发射波形设计的方法来抑制从雷达主瓣方向进入的干扰成为研究的热点之一。粘朋雷等提出了根据线性调频信号(LFM)起始频率不同的特点，将接收信号移频，使目标信号无脉压输出，得到干扰信号和目标信号在时域的不同位置将其分开[8]，达到抗干扰的目的。Rohling等设计了一种滤波器，利用使互相关函数旁瓣为零的特性来优化滤波器的系数，但是该方法会导致信噪比有一定的损失[9]。Li等设计了一种基于阻塞滤波的抗主瓣干扰系统，但是该系统形成目标功率图时，会导致在不同距离上出现不同程度的抬高，给目标的检测带来了困难[10]。

1 雷达发射信号模型及性质分析

1.1 Frank编码性质分析

为了能够从信号的时域出发，设计出与发射信号正交的滤波器，选取Frank码作为发射信号的相位编码矩阵。Frank编码是由海米勒(Heimiler)和法兰克(Frank)共同提出的，长度为m2的Frank编码可以由Frank矩阵组成。设Frank编码矩阵第p行第q列的元素为xpq，则

xpq=exp[j2π(p-1)(q-1)/m]

(1)

Frank编码矩阵作为一种特殊的矩阵，具有以下性质：

1) 正交性

设X为M×M维矩阵，xij为矩阵第i行、第j列元素：

(2)

则第i行的自相关函数为

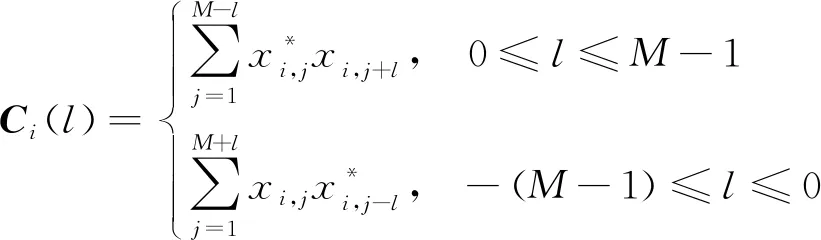
(3)

Frank编码矩阵是一组正交的编码矩阵，得到的各子码的自相关函数，将其相加得到的结果除了匹配点之外，其余值均为零。

(4)

可以利用Frank编码这一性质，使用式(4)进行多通道匹配滤波处理，这样可以获得较低的旁瓣。为了使得到的旁瓣更低，本文采用切比雪夫窗对Frank编码矩阵的旁瓣进一步抑制。

2) 零互相关性

Frank编码的任意两行的互相关函数为零，即Frank编码任意两行的元素互不相关。设Frank编码矩阵中的第i行与第j列(i≠j)的互相关函数为Gij(k)，则

(5)

根据Frank编码的这一特性，可以设计出与发射信号相对应的阻塞滤波器组，将目标信号滤除。

1.2 信号模型

用Frank编码对发射信号进行相位编码，从而得到雷达的发射信号，具体编码规则如图1所示。

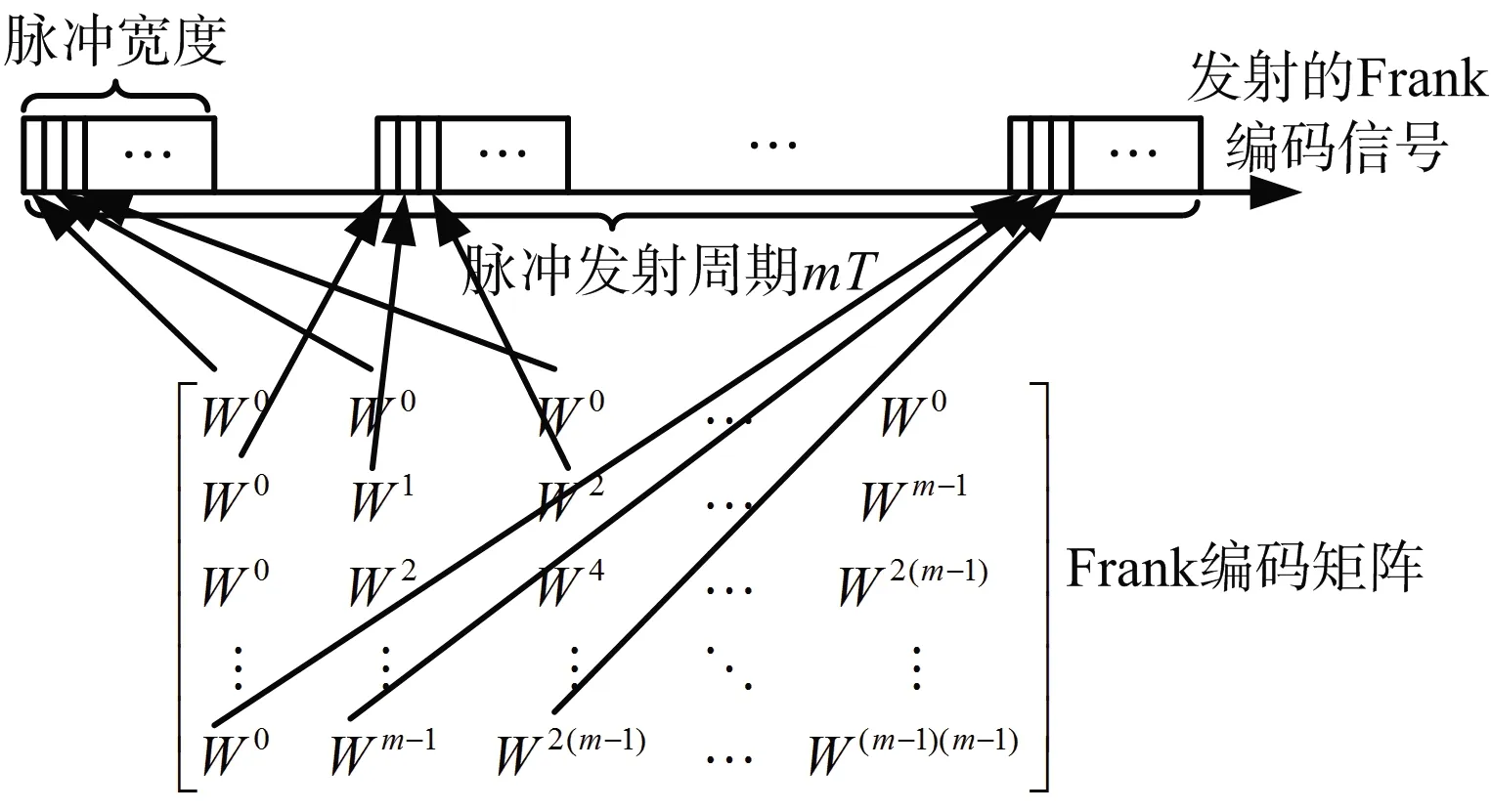
图1 雷达发射经Frank编码相位调制后的信号

假设每个脉冲的周期为T，脉冲组的周期为mT。每个脉冲的脉冲宽度为τ，在每个脉冲宽度τ中又均分为m个子脉冲，利用Frank编码矩阵的第i行对第i个脉冲进行编码，其中编码矩阵中第i行中第k个元素对应于第i个子脉冲第k个相位。

假设发射信号的幅度为A,子脉冲宽度为τsub=τ/m，则在一个脉冲组内，第i个脉冲编码信号为

(6)

令多相位编码信号的幅度调制函数为

(7)

则发射信号可以写为

Si(t)=ψi(t)exp[j(2πf0t+φin)]

(8)

假设目标信号距离雷达为R0，并且以速度v0向雷达径向运动，则第i个脉冲信号的回波信号为

(9)

式中，τ=2(R0+vt)/c。

2 基于阻塞滤波器的抗主瓣干扰算法

2.1 阻塞滤波抗干扰系统

阻塞矩阵抗主瓣干扰方法抑制系统信号处理流程如图2所示。系统主要有3个模块组成，分别为匹配滤波处理模块、阻塞滤波处理模块和自适应对消处理模块。

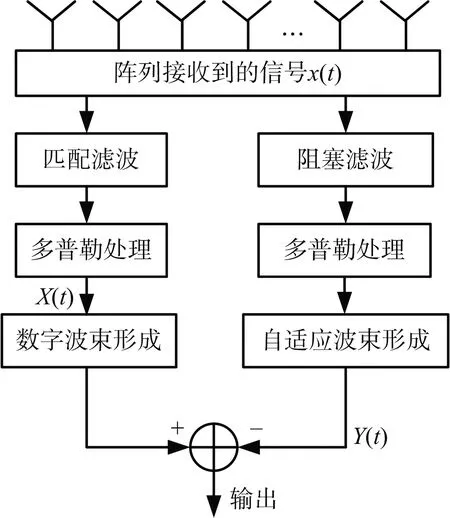
图2 信号处理流程图

(a) 匹配滤波处理模块

主通道中的匹配滤波处理模块是对接收数据进行匹配处理，其目的是为了让输出信号的信噪比达到最大。匹配滤波的冲激响应函数可表示为

h(t)=kS*(t0-t)

(10)

式中，S(t)为雷达发射信号，t0为脉冲积累时间。然后沿着脉冲维对数据进行多普勒处理，得到目标信号回波的距离-多普勒数据。

(b) 阻塞滤波处理模块

辅助通道中的阻塞滤波处理模块对阵列接收到的信号进行阻塞滤波处理，其目的是将目标信号从回波信号中滤除，得到回波信号中干扰和噪声的估计。阻塞滤波利用的是Frank编码矩阵各行之间零相关的性质，由于编码矩阵中任何一行子码和其他子码都是正交的，因此，除本身以外的任何子码信号行都可以作为该子码阻塞滤波器的冲激响应。各通道冲激响应可表示为

hb(t)=kS′*(t0-t)

(11)

式中，t0为脉冲积累时间，S′(t)为与发射信号S(t)正交的信号。可知经滤波后的回波信号中的目标信号被抑制，仅包含外部干扰和噪声。

(c) 自适应旁瓣相消算法

旁瓣对消算法是通过自适应的改变辅助阵列的权值来改变天线的方向性，实现在空域中信号的方位增强，而在干扰的方位形成波束零陷，达到将干扰信号滤除的目的。假设N个阵列天线接收到的信号yn(k)作为信号处理的主通道，为了不增加系统的硬件复杂度，将天线所有阵列接收到的信号作为信号处理的辅助通道，记为xn(k)，xn(k)=yn(k)=[xn1,xn2,…,xnm]T。主通道中经匹配滤波处理单元后的数据记为Y(k)，辅助通道经阻塞滤波处理单元后的数据为X(k)，其中k为采样点数。则由最小均方误差准则可以得到最优加权矢量为

(12)

式中，RXX=E[XXH],RXY=E[XYH]。

2.2 基于目标数据剔除的阻塞滤波抗干扰系统

由于上述方法在旁瓣对消后会导致目标所在距离旁瓣电平升高等问题，不利于目标的检测。而导致距离旁瓣电平升高的原因为当干扰从目标相同方向进入雷达天线时，在计算目标所在多普勒单元的权值时，主通道中包含信号、干扰和噪声，而辅助通道中仅包含干扰和噪声，造成两通道之间的能量瞬时增大，所以计算权值时所得的权值也突然增大，造成了目标所在多普勒单元的距离旁瓣电平突然增高。

根据上述分析，为减小目标所在多普勒单元的旁瓣电平，在进行权值计算时，将目标所在距离多普勒单元的数据去除，使得在计算目标所在多普勒单元时，主通道和辅路通道的能量相差不会太大，距离旁瓣不会有明显的升高。而对于目标所在距离多普勒单元的获取，可以利用上述阻塞滤波抗干扰系统大致找到目标所在距离多普勒单元。信号处理流程如图3所示。

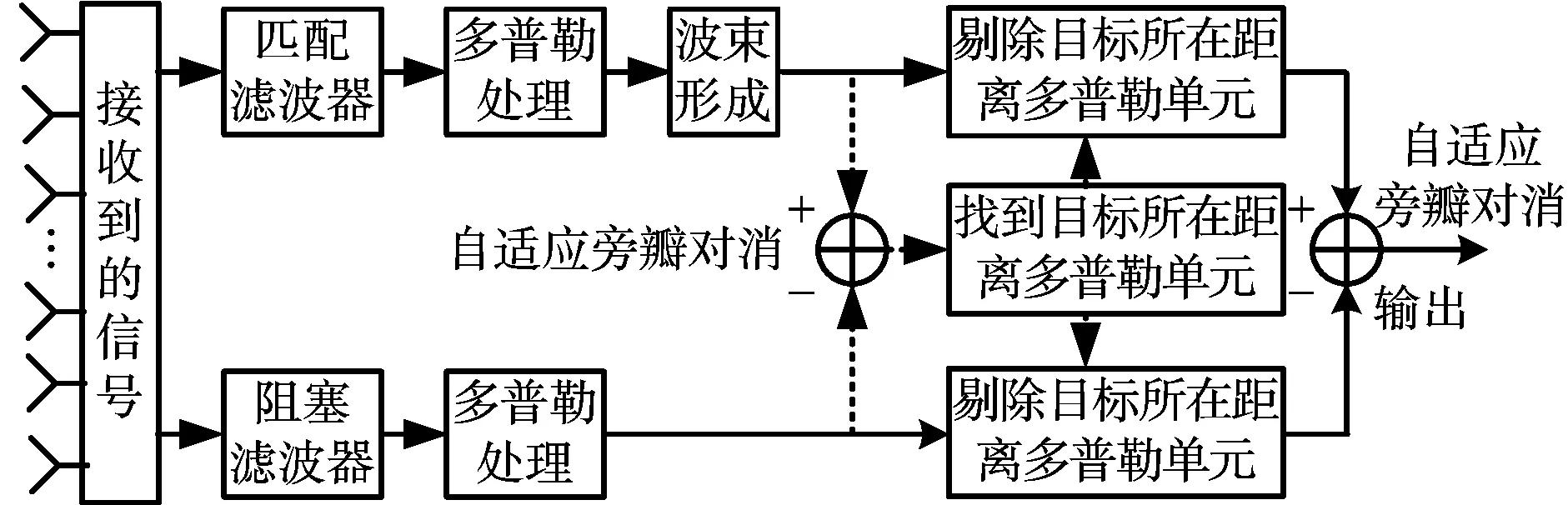
图3 改进的基于目标数据剔除的抗干扰方法流程图

3 仿真实验及分析

图4为目标信号和从主瓣进入的同载频干扰共同形成的距离-多普勒频率图，从图中可以看出目标信号已经被干扰信号淹没，无法正常检测出目标所在位置。图5为接收信号分别通过匹配滤波器和阻塞滤波器后，再经过旁瓣对消后形成的距离-多普勒频率图，从图中可以看出经过该算法处理后，目标信号已经非常明显，但从图中可以看出，在目标所在多普勒频率单元上，目标所在距离门旁瓣相对其他多普勒频率距离门旁瓣高了许多，不利于目标的检测，在干扰较强时，甚至无法对目标进行有效检测。

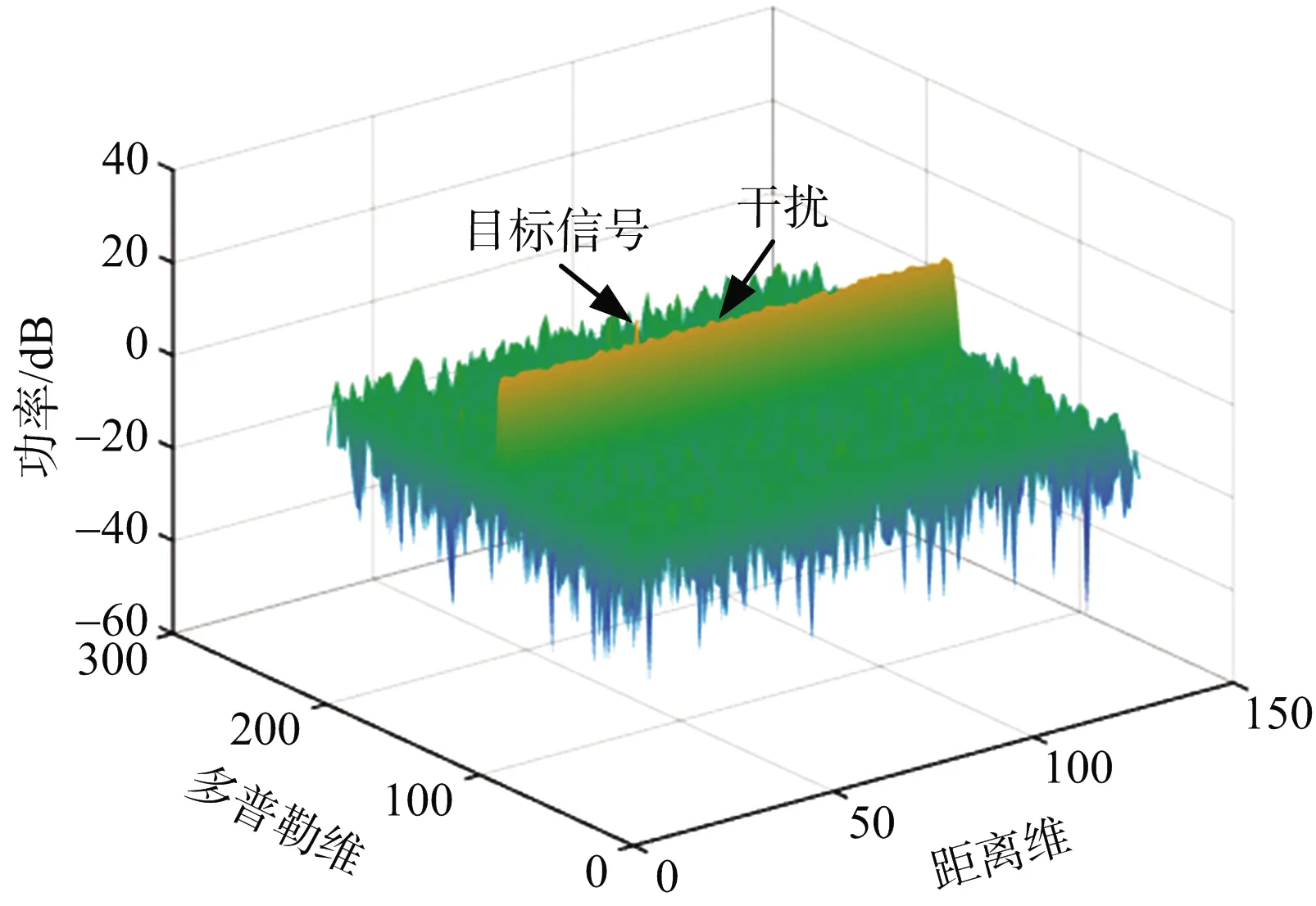
图4 旁瓣对消算法前距离-多普勒频率图

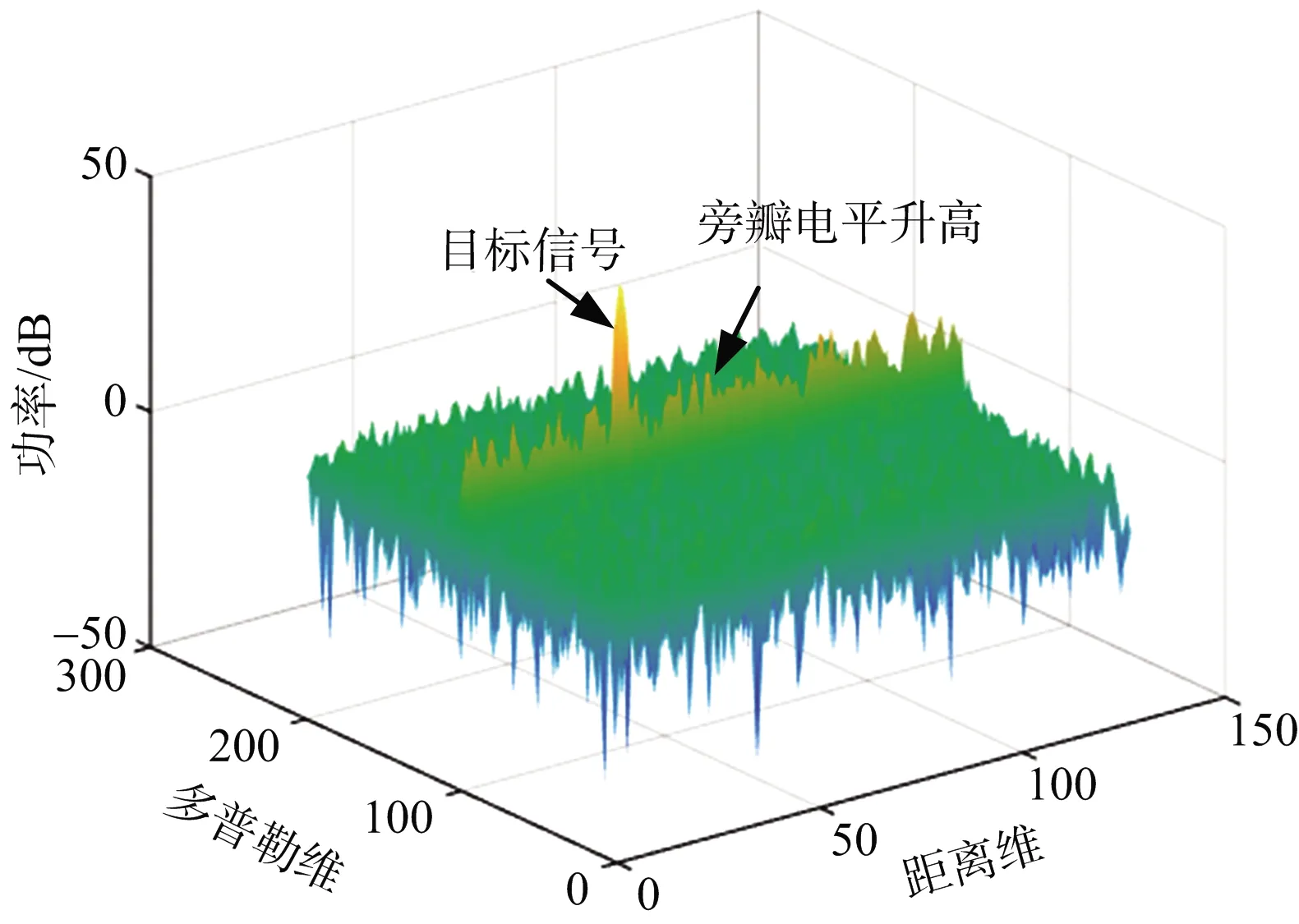
图5 旁瓣对消算法后距离-多普勒频率图

图6 改进旁瓣对消算法后距离-多普勒频率图

实验二：仿真条件与上述相同，从图6可以看出经改进后的算法和原来的算法相比，改进后的算法在目标所在的多普勒频率维上，目标所在距离旁瓣得到了有效抑制，目标信号所在位置非常明显，更有利于目标的检测。图7为旁瓣对消算法和改进后的算法目标所在多普勒维的切片对比图，从图中可以看出，改进后的算法目标能量几乎没有变化，而距离旁瓣电平降低了15 dB。

图7 改进前后目标所在多普勒频率切片对比图

4 结束语

当干扰从雷达的主瓣方向进入雷达天线系统时，传统的旁瓣对消系统会导致波束变形、波束指向偏移等问题。针对这一问题，本文利用Frank编码的正交性和零互相关性设计出发射信号的匹配滤波器和阻塞滤波器，分别将信号通过两滤波器，得到两路信号，然后利用旁瓣对消算法将主通道中的干扰对消掉。通过仿真发现，当目标信号较大时，主通道和辅路通道的能量相差较大，导致目标所在多普勒频率单元的距离旁瓣会升高，不利于目标信号的检测。为了进一步降低目标所在多普勒单元的距离旁瓣，本文提出了改进算法，将目标所在距离-多普勒频率单元的数据去除后，再进行权值的计算。通过仿真表明，改进后的算法可以有效地将目标所在距离旁瓣降低，相比于其他算法而言，本文提出的算法具有不需要增加额外的硬件设施、算法复杂度较低等优点，为抗主瓣干扰提供了新思路。