三个“把握”优化学生思维

梁静雯

【摘要】 美国认知心理学家布鲁纳认为：儿童认知的成长过程会经过三个把握阶段，即： 行为把握（从动作中发展认知）、图像把握（由直观图像来发展认知）、符号把握（接受语言符号的信息来发展认知）。 于是本课则按照“充分感知——建立表象——抽象概括——巩固内化” 的步骤来开展教学。 实践证明，这样做有助于学生立足于具体事物的形象去理解抽象的数学概念和掌握计算公式，有利于学生建构初步的空间观念和发展创新意识，让学生的思维能力进一步向上发展。 当然，如果只过分强调形象思维，则很容易走入思维的单一性的狭隘空间，于是，数学教学中的我们在抽象与直观间建立了一条适度的平衡线，不断地经历图像、文字、符号之间的切换，使学生的直觉、形象思维上升到理性思维的层次。

【关键词】小学数学;教学思维

学生数学核心素养的重要组成部分之一便是数学思维，数学思维水平会直接影响学生解决数学问题的能力。在当前的数学教学中，学生对具体的、形象的内容最感兴趣，然而对抽象的内容则不易吸收。因此在本课的教学中，我着重于把握学生已有的认知规律，引导学生有序地探寻规律，交流探索包装方法的多样化，体验多样化的策略，然后再进行对比，逐一筛选，把握一个本质规律便是“重叠面积越大，包装纸越少”。

一、唤醒经验，把握起点

无论学什么，学生都不是一张白纸，他们拥有丰富的生活经验，并或多或少地以先前的知识技能作为基础，从而再进一步学习新知识。

教学中，笔者创设情境一：现在我有一盒糖果（长是11厘米，宽是8厘米，高是4厘米），想给它包装一下，至少需要多少包装纸（接口处不计）？这个问题需要用到长方体的哪些知识呢？有学生根据经验算出该长方体的表面积是（11×8+11×4+8×4）×2=328平方厘米，知道需要328平方厘米的包装纸。此处，笔者有意识地抛出问题，让学生有意识地知道在接口处不计的情况下，生活中需要多少包装纸与长方体的表面积相联系，关注了学生的已有经验，准确把握学生的学习起点，便于找到新知的着力点，有效地节约课堂教学时间，提升教学时效。

二、重视操作、把握过程

“纸上得来终觉浅，绝知此事要躬行。”学生的学习过程不能由老师包办、只有让学生经历充分的体验，才能内化新知。

（一）动手操作，提升抽象思维

通过情境一的铺垫，笔者继续引导学生思考：两盒糖果包成一包，你会怎么包装？ 说说它的长宽高，怎样子求它需要多少包装纸？这里，学生借助于学具的摆弄，以小组合作的方法去探究如何把两盒糖果包装成一包， 并通过平板电脑把各种各样的包装方法拍下来，上传到云端，这样所有学生的摆法都得到了展示， 老师也能快速地把全班的摆法都浏览一遍。 随后全班一起总结，发现共有三种包装方法，第一种是2个大面重合，第二种是2个中面重合，第三种是2个小面重合。并由学生口述其包装方法需要多大包装纸的计算方法。

苏霍姆林斯基说过：“手和脑之间有着千丝万缕的联系，手使脑得到发展，使它更加明智，脑使手得到发展，使它变为思维的工具和镜子。”可见学生的思维是从动手操作开始的，因此在教学中教师应当根据教学内容和学生的已有经验，抓住学生的思维特点，为学生提供丰富的情境材料，让学生多动手、从而把这些动手经验转化为学生认知结构中的一部分，为他们的本节学习提供宝贵的学习财富。学生便在旧知的基础上，运用计算长方体表面积的公式很快地算出三种包装方法各需多少包装纸，通过比较发现第一种包装方法是节省包装纸的。

（二）动手验证，引发数学思考

在日常教学中，我们必须根据教学内容和学生的认知思维规律，把握学生的思维特点，为学生提供丰富的背景材料与动手操作机会后，引发学生进行数学思考。

通过上面的动手操作，已经有一小部分学生会自己猜测到底哪种方法是最节省包装纸的，在思考片刻后，学生的猜测便通过计算进行验证。我接着又让学生猜，为什么第一种方法是最节省包装纸呢？ 学生指出因为第一种方法重合了两个大面。 如何验证这个猜想呢？ 除了计算出长方体的表面积以外，另外，也可以使用这一方法：总表面积-重叠的两面面积之和=包装纸的面积。计算对比后，发现确实是第一种方法最节约包装纸。继续追问学生，引发学生进行数学思考。 学生就会用自己的语言述说：由于两个原长方体的面积之和是一样的，减去的重叠面积越大，则包装纸的面积越小;减去的重叠面积越小，则包装纸的面积越大。 教师则适时总结：要想知道谁最节约包装纸，关键要找出重叠的面积的大小，重叠面积越大、则包装纸的面积越小。

面对三种包装策略，最优的方法应从最节约包装纸的角度来寻找的，一开始需要学生凭借经验来合理猜测，接着通过计算来验证。而计算的方法也是多样的，有根据以往经验算表面积，也有用总面积-重叠面积=包装纸的面积，而笔者引导学生着重关注后者方法，采用追问的方式引导学生分析计算结果，再与操作结合，使学生聚焦于重叠面积的大小与包装纸面积大小的联系，体验到重叠面积越大，则包装纸的面积越小。从表到里地把学生的思维引向深处，不断优化学生思考问题的途径，从而发展了推理能力与反思能力，为后续的探究道路指明了方向。

（三）动手思考，培养思维能力

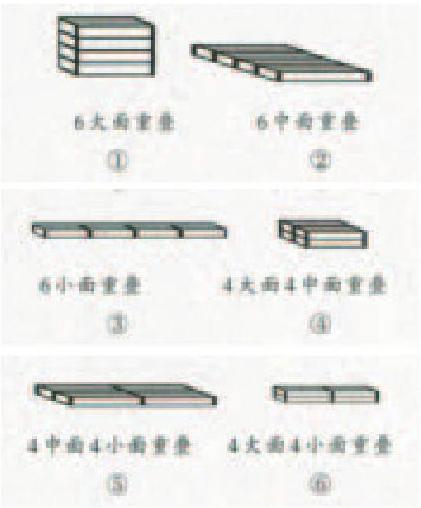
教学中，笔者创设了情境二：4盒同样的糖果盒打包成一包，有几种包装方案？学生自主操作摆一摆，发现一共有以下6种包装方法。 “那谁最节约包装纸呢？ ”引发猜想，发现并没有学生认为②和③是最节约包装纸的。因为学生通过情境一已初步知道重叠面积越大，包装纸面积越小，学生运用了新知和直观的感受，知道①重叠6个大面的面积>②重叠6个中面、①重叠6个大面的面积>③重叠6个小面的面积， 因此排除了②和③，而其余4种方法的重叠面积则需要学生进一步分析，因此学生都在这4个选项里徘徊。

那我们便请学生在小组里讨论一下各自摆法重合了什么面，如何判断谁更节约包装纸。①重叠6个大面;④重叠4个大面和4个中面;⑤重叠4个中面和4个小面;⑥重叠4个大面和4个小面。由于④⑤⑥都重叠了几种面积大小，所以学生一时间很难进行准确判断，而这时就需要他們讨论、分析、并大胆猜测。学生在与同伴思维的碰撞后，会发现④重叠4个大面和4个中面的面积⑤重叠4个中面和4个小面的面积，因此排除⑤;④重叠4个大面和4个中面的面积>⑥重叠4个大面和4个小面，因此也排除⑥。剩下①和④，就很容易比较了，学生很快就计算后得出：①重叠6个大面>④重叠4个大面和4个中面，所以方案①重叠6个大面是最节省包装纸的。

数学的基本思维方式之一便是推理，我们在学习和生活中也经常使用到这种思维方式。在这，学生从已有的事实出发，知道大面积>中面积>小面积，接着凭借着经验和直觉，通过归纳和类比的方法先排除某几种摆法，再通过计算确定结果。在这一系列顺其自然、顺学而导的教学过程中，学生的合情推理能力必然得到有效的提升和发展。

三、适度抽象，把握本质

数学教学的最终目的是探究知识的本质。我们的教学不能停留在表面的热闹有趣，而应该带领学生在有趣的环节中继续深入，揭开表面现象的理解，在充分地感知后适度抽象，直达数学的本质。

如果没有数学思维，数学学习便谈不上是真正的确确实实的学习。 在解决包装两盒磁带时，让学生自己动手摆放、比较、交流，给予他们自主思考、自主探究的时间，让他们充分体验解决问题的基本过程和方法。 当学生体验解决策略多样化的同时，再引导他们进一步探究最优策略，通过探究最后得出：重叠面积最大，包装纸面积就最小，从而知道这是最节约包装纸的。 让学生根据看到的事实进行推断和解释，养成“推理有理有据”的习惯，在推理过程中不断反思自己的思考过程; 在与同伴交流多样策略时，能与他人进行有效沟通，并使学生能够理解他人的思考方式和推理过程。

克罗韦尔指出：“教育面临的最大挑战，不是资源，不是技术，不是责任感，而是需要教师和学生一起去发现新的思维方法。”所以，教学中应着重进行学习者的头脑思维锻炼，发展学习者的思维能力。从包装1盒糖果，复习旧知，让学生从已有的知识水平和思维水平出发，先让思维打开、活跃起来; 到包装2盒糖果、4盒糖果探究新知时，教师给学生设置思维障碍，使学生产生“山重水复疑无路”之感，又要循循善诱，让学生通过自身兴奋的头脑思维活动找到解决问题的路子。最后不断完善、总结最节约包装纸的包装方案：不仅要考虑是否重叠了最大的面，还要考虑重叠最多的面才能减少最大的面积。我们要为学生创造一个思维阶梯，鼓励学生进行动手操作，使他们的思维和直觉更直接、更快速、更深入，从而真切感受到成功果实的甜味。

参考文献：

[1]俞秉钧.关注图像学习，彰显思维价值[J].小学数学教育，2016.

[2]陈晓燕.把握转化三要素，有效渗透转化思想[J].小学数学教育，2016.