基于循环平稳的疲劳损伤检测方法
2020-03-27王猛松张二亮李大磊
王猛松,张二亮,李大磊
(郑州大学机械工程学院,河南 郑州 450001)
1 引言
疲劳是零件或构件的主要失效形式,据统计,大约有80%的机械断裂事故是由疲劳失效引起。疲劳损伤检测一直是材料、机械、力学的研究热点,关键是要找到对疲劳损伤演化敏感的损伤变量,国内外疲劳损伤检测发展了很多方法,如固有频率法、塑性变形能法、刚度法、弹性模量法、金属磁记忆信号法等[1-2]。刚度法和固有频率法基本思想是,在疲劳损伤过程中,刚度逐渐减小,引起动态响应固有频率不断下降,可用固有频率和刚度的变化规律来监测损伤[3-4];金属磁记忆信号法基本思想是磁信号在稳定循环阶段随疲劳循环周次增加无显著改变,疲劳裂纹萌生后,磁信号逐渐增加,并在断裂后发生激变,可基于磁记忆信号建立疲劳损伤累积模型[5]。弹性模量法基本思想是低周疲劳过程表现为弹性模量的下降和名义应力的衰减,可用弹性模量研究疲劳损伤累积[6]。
循环平稳理论在信号处理中的应用始于20世纪80年代中期,研究的是一类特殊的非平稳信号,它的统计参量,如均值和自相关函数,是时间的周期函数。循环平稳信号处理方法广泛应用在旋转机械故障诊断领域,并取得了很多成果,引起广泛的关注[7]。二阶循环统计量能反映循环平稳信号中隐含的周期性成分,该周期性成分与齿轮、轴承等的故障信息有关。常用的二阶循环统计量主要有循环自相关函数、谱相关密度函数和谱相干函数[8]。疲劳试验机与疲劳试样组成的试验系统在循环加载下,其振动信号也属于循环平稳信号,可将该方法用于疲劳损伤的检测。在循环平稳理论基础上,提出了一种基于循环平稳的疲劳损伤检测方法。通过采集金属试样在疲劳过程中的振动信号,使用循环平稳信号处理方法进行分析,可得该振动信号的谱相关密度函数,再基于谱相关密度函数建立监测变量,通过定义的监测变量可在线描述疲劳损伤累积状态。并开展疲劳试验和数值仿真验证该方法的可行性。
2 循环平稳理论与算法
2.1 循环平稳理论
循环平稳信号具有周期变化的统计量称为循环统计量,根据统计量的不同,循环平稳信号可分为一阶(均值)、二阶(自相关函数)和高阶循环平稳[9]。
谱相关密度函数可同时显示频域能量的变化和波形的演化。循环平稳信号r(xt)在t时刻一个时间间隔τ的瞬时自相关函数(τ)是时域上的周期函数,可通过傅里叶展开,如式(1):

式中:f—原始信号的谱频率;α—信号的循环频率,表示循环平稳性信号隐藏的周期形成分的频率,循环频率是离散的,A—一个包含所有循环频率α的集合。二阶循环统计量可将能量流分解成周期性部分,反映与周期性相关的能量随时间变化规律。
2.2 循环平稳算法
循环平稳信号x(t)可以分解为确定性部分mx(t)和残余部分rx(t),确定性部分就是均值,包含信号的所有周期性成分,可由原始信号同步平均得到,其策略,如图1所示。可基于残余部分rx(t)求取谱相关密度函数。
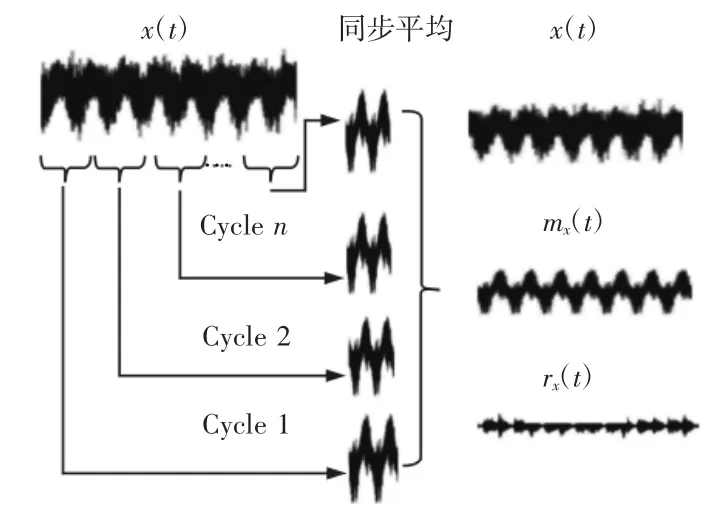
图1 同步平均Fig.1 Synchronous Average
谱相关密度函数是一个理论值,平均循环周期图法(ACP)、循环调制谱法(CMS)、快速谱相关法(Fast-SC)是三种谱相关密度函数估计量的求取方法[10]。采用快速谱相关法估计谱相关密度函数。ACP是一个常用的估计量,但算法效率较低。CMS算法中谱频率不能取很高分辨率,影响谱相关密度函数估计精度。Fast-SC在前两种方法基础上发展而来,能够快速准确估计谱相关密度函数。
快速谱相关法的基本过程,首先对循环平稳性信号加窗并进行短时傅里叶变换,如式(3):
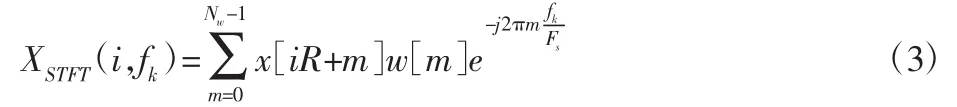
式中:Nw—一个窗的长度;R—两个连续窗的间隔;w[m]—窗里的数据,fk=kΔf,k=0,…,Nw-1,如图 2 所示。谱频率分辨率 Δf=Nw/Fs,Fs—采样频率。
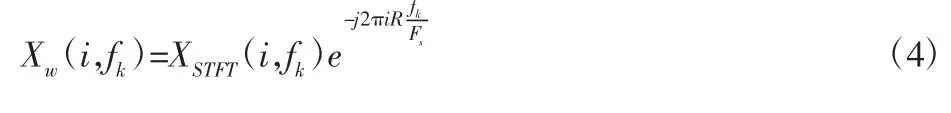
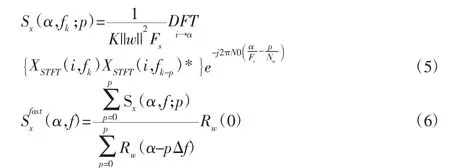
式中:Xw(i,fk)—带宽为Δf的复包络,p的取值为0,…,Nw/2R,将式(3)~—(5)代入式(6)可得谱相关密度函数的快速谱相关估计量。详见文献[12]。
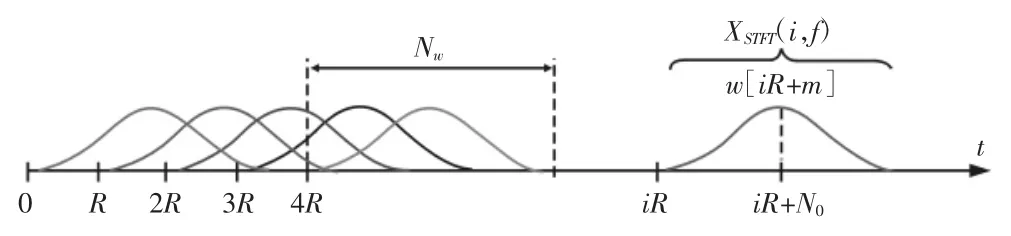
图2 短时傅里叶变换参数图解Fig.2 Illustration of Parameters in the Short-Time Fourier Transform
3 监测变量
采集的整个疲劳过程的循环平稳信号需要分段进行处理,每段的时间过长,会导致部分信号特征的湮没,划分过细会导致信号处理效率降低,应选取适当的分段长度。再使用循环平稳算法对信号处理,得到每一段时间内的谱相关密度函数,寻找谱相关密度函数变化与疲劳损伤演化之间的关系。
可用谱相关密度函数的变化反映疲劳损伤累积,为了更直观的描述谱相关密度函数随疲劳损伤的演化规律,需定义一些监测变量,如循环频率谱区(CFSA)[10]。循环频率谱区如式(7),是将谱相关密度函数上不同频率和循环频率对应分量的累加,将谱相关密度函数随疲劳累积的变化特征集中体现;

4 仿真算例与实验验证
4.1 仿真算例
4.1.1 仿真模型
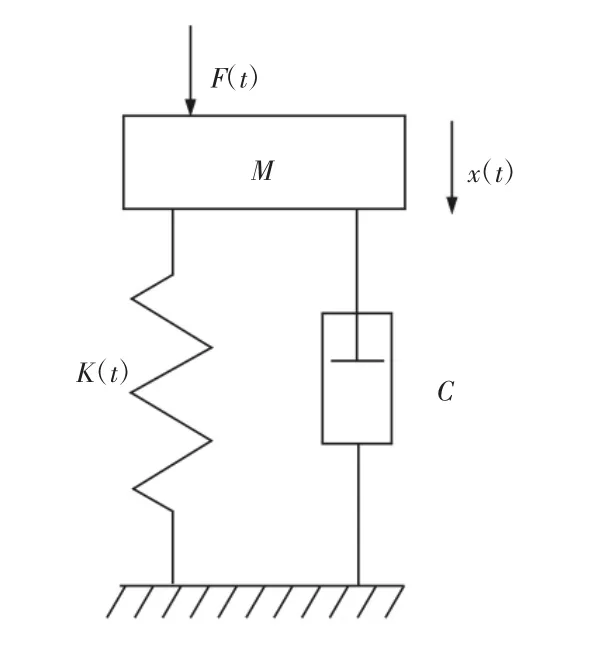
图3 单自由度模型Fig.3 Single Degree of Freedom Model
单自由度模型来模拟承受循环载荷的金属试样,如图3所示。该单自由度系统的平衡方程为:

通过单自由度模型仿真疲劳试样的振动信号,来研究疲劳损伤规律。在疲劳实验当中,因疲劳裂纹的变化,试样的刚度会随着时间改变。在该模型当中定义了裂纹张开和闭合时的刚度变化规律,刚度模型为[2]:

式中:ω0—裂纹开闭频率;k0—裂纹完全张开时的刚度,定义k0在疲劳过程中线性衰减;刚度变化的幅值定义为:-k0);kc—裂纹闭合时的刚度。
4.1.2 Simulink仿真及结果分析
为了仿真承受循环载荷的金属试样的振动响应,结合单自由度模型,可对的试样振动过程进行Simulink数值仿真,可以得到试样在刚度随时间变化情况下的响应x(t),该位移信号理论上应具有循环平稳性,下面将使用循环平稳信号处理程序分析x(t),寻找每一段时间内的谱相关密度函数与疲劳损伤演化之间的关系。通过仿真得到疲劳试样位移信号,如图4所示。再用循环平稳信号处理程序分析振动信号,可以得到每一段时间内的谱相关密度函数。
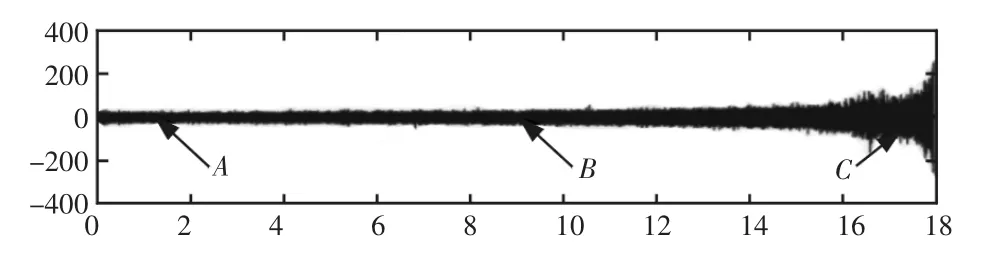
图4 仿真的位移信号Fig.4 Simulation of Displacement Signal
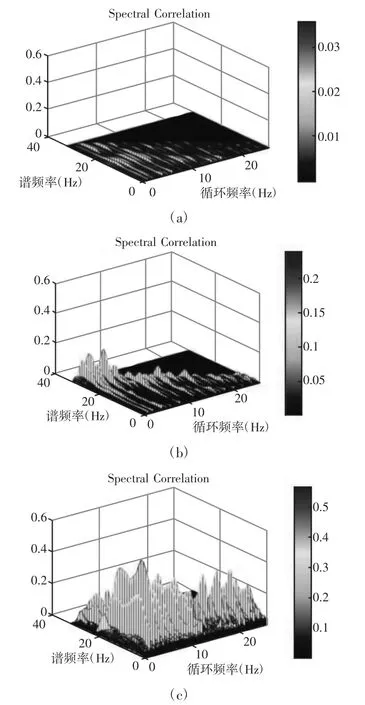
图5 仿真信号的谱相关密度函数Fig.5 The Spectral Correlation Density Function of the Simulation Signal
在振动信号A、B、C三个阶段的谱相关密度函数,在不同循环频率下,能够观察到均匀分布的波峰,对应基频和各个倍频,说明该信号符合循环平稳信号的特征,如图5所示。随着疲劳损伤演化,谱相干密度函数图像发生明显变化,幅值呈上升趋势,说明疲劳过程中,周期性的冲击摩擦不断加剧,试样的损伤累积导致其物理性能逐渐削减。该仿真结果验证了使用循环平稳信号处理方法来检测疲劳损伤的可行性。疲劳过程中每一段时间内的谱相关密度函数对应的CFSA,如图6所示。可看到CFSA值随着疲劳损伤的累积不断增大,说明该循环平稳性监测变量可以很好地反映疲劳损伤的累积,因此可在疲劳试验中,通过采集试样振动信号并计算其监测变量,来检测疲劳损伤。
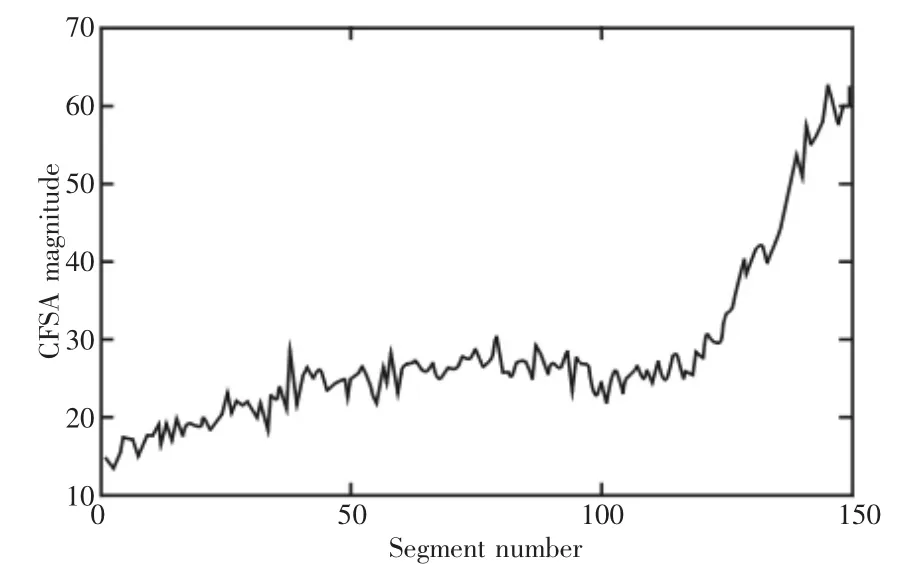
图6 疲劳过程的监测变量CFSAFig.6 The Monitor Variable CFSA of the Fatigue Process
4.2 疲劳试验
4.2.1 材料及试验方法
为了进一步验证循环平稳信号处理方法在金属试样疲劳损伤中的敏感性,使用MTS液压伺服试验机开展了疲劳试验,并用信号采集器采集疲劳过程中的振动信号。圆柱疲劳试样,材料是45号钢,长度为160mm,危险截面直径9mm。疲劳试样采用正弦加载,应力比为-1,幅值30kN,加载频率8Hz。搭建的疲劳试验系统,如图7所示。传感器的固定位置如夹具的局部放大图所示,使用传感器采集疲劳过程中试样的振动信号。

图7 疲劳试验系统Fig.7 The Fatigue Test System
4.2.2 试样结果分析
疲劳试样断裂后,对整个疲劳过程的振动信号使用循环平稳信号处理方法进行分段处理,可以得到各个时间段试样振动信号的谱相关密度函数,疲劳开始,疲劳中和疲劳断裂前的谱相关密度函数,在不同的循环频率下,同样可以观察到均匀分布的波峰,如图8所示。非零循环频率下分量不为0,说明循环加载的疲劳试样的振动信号属于循环平稳信号。并且随着疲劳损伤的演化,谱相关密度函数的幅值有增大趋势,表示循环平稳信号处理方法对试样的疲劳损伤是敏感的。
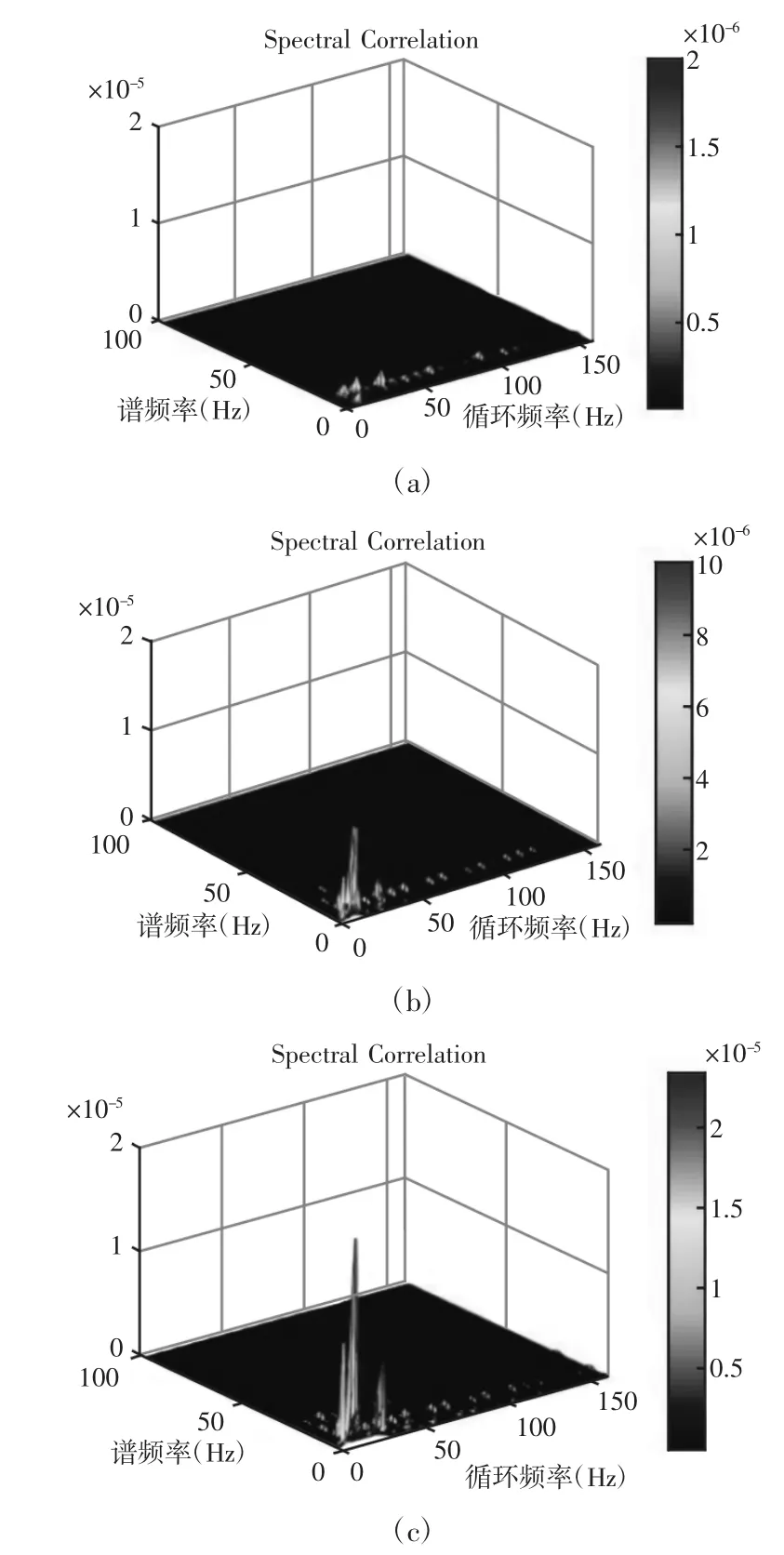
图8 试样振动信号的谱相关密度函数Fig.8 The Spectral Correlation Density Function of the Sample Vibration Signal
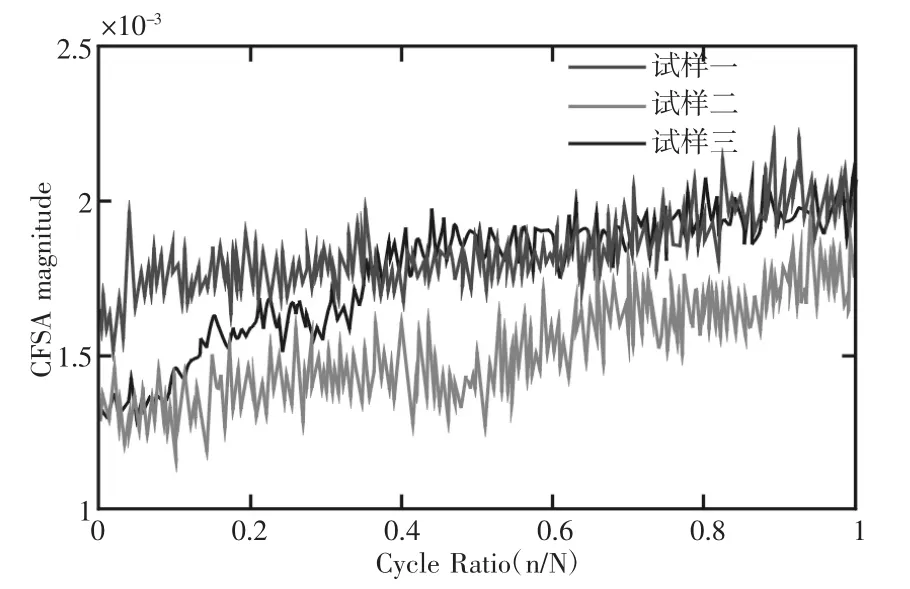
图9 疲劳过程中的监测变量CFSAFig.9 The Monitor Variable CFSA of the Fatigue Process
将周期数归一化,每个试样的疲劳过程分为N段,n表示当前段,分别对三组低周疲劳数据处理可得到监测变量CFSA在疲劳过程中的变化规律,如图9所示。在疲劳过程中,随着疲劳损伤的不断累积,监测变量CFSA逐渐增大。
5 结论
通过仿真算例和实验验证,证明了基于循环平稳的疲劳损伤检测方法的可行性,循环平稳信号处理方法可用于检测疲劳损伤累积,定义的监测变量CFSA在低周疲劳中随着试样内部冲击摩擦的加剧,幅值逐渐增大,即监测变量CFSA与疲劳损伤累积呈正相关关系。
