基于深度确定性策略梯度算法的双轮机器人平衡控制研究
2020-03-27刘胜祥林群煦杨智才吴月玉翟玉江
刘胜祥, 林群煦, 杨智才, 吴月玉, 翟玉江
(五邑大学轨道交通学院,广东江门529020)
0 引 言
随着人工智能的兴起,强化学习在人工智能领域占据着一个重要的位置,强化学习现在主要应用于机器人的控制、网络游戏中的电脑玩家等方面[1]。倒立摆是一种高阶次、非线性、连续,多变量的不稳定系统。对于倒立摆平衡控制问题,国内外许多学者提出了各种强化学习算法,例如演员评论家、神经网络等。然而基于倒立摆平衡原理研制的双轮机器人大部分使用PID控制,但PID控制需要多次调整参数,同时经典PID控制中的积分在无扰动时,系统的动态特性变差。
本文将深度确定性策略梯度算法应用于双轮机器人的平衡控制,以解决深度强化学习在双轮机器人中应用的问题。该算法无需建立复杂模型,只需算法给出动作对双轮机器人的姿态进行调整。深度确定性策略梯度算法以机器人与水平地面的角度作为状态,驱动轮的运动作为动作,并使用角度信息构建奖励函数,有效地改善了双轮机器人直立状态时的平稳性。针对深度确定性策略梯度算法收敛问题,提出了分层奖励的方法,提高了经验池的学习效率,加快了学习速度。同时针对在实验中遇到的延时问题,提出了回转策略的方法。
1 相关理论
1.1 强化学习分类
强化学习的一种分类方法可分为基于概率(Policy-Based)和基于价值(Value-Based)[2]。基于概率的强化学习算法通过感知周边的状态信息,直接得出下一步要输出的不同动作概率,然后根据概率输出动作,此类算法通常用于连续动作,但无法表示连续动作的价值,主要算法有策略梯度算法等;基于价值的强化学习算法输出所有动作的价值,根据最高价值来选择动作,但无法用于连续动作,主要算法有Q学习、Sarsa等。
1.2 行为者评论家算法
行为者评论家算法(Actor_Critic)结合了两类算法的优点,算法包含一个策略网络(Actor)和一个价值网络(Critic)。如图1(a)所示的策略网络结构图,输入状态s,输出动作a。如图1(b)所示的价值网络结构图,输入为动作和状态s,输出为Q(s,a)。
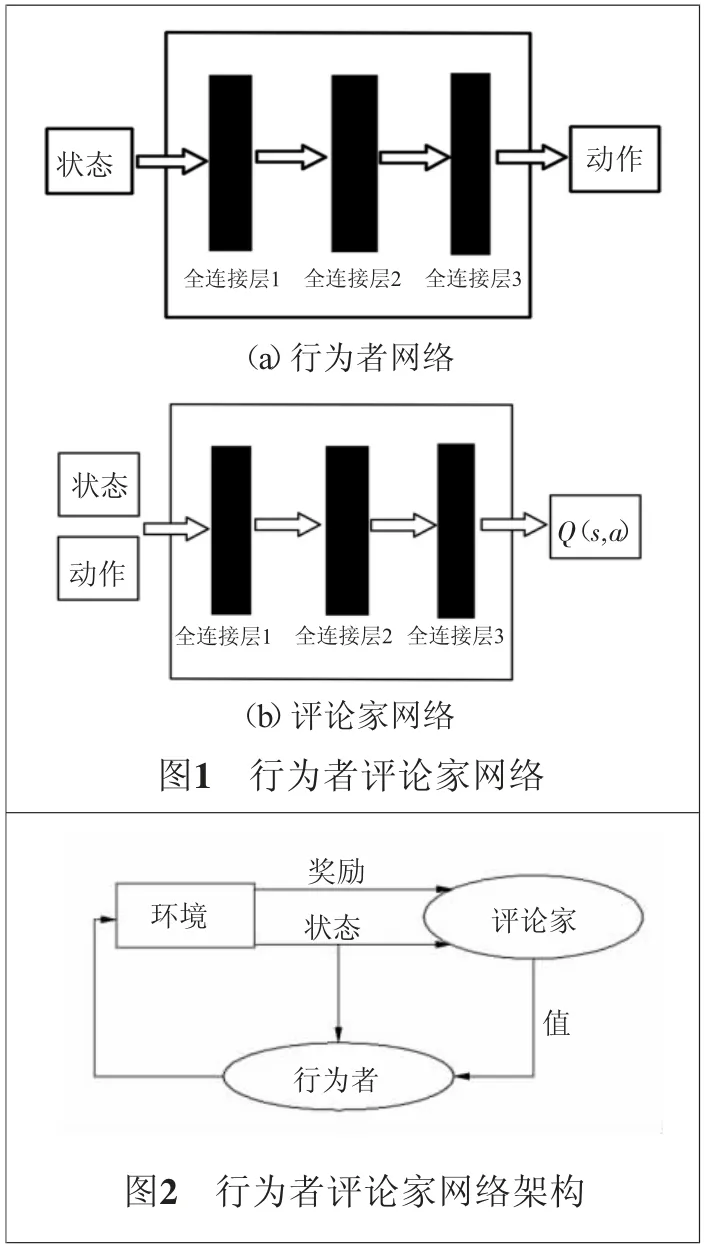
行为者评论家算法的网络架构如图2所示,行为者网络和评论家架构是将策略梯度和状态行为值函数相结合。行为者网络的作用是通过调节参数来确定状态下的最佳行为,评论家网络的作用是评估行为者网络产生的行为。评论家网络是通过计算时间差分误差来评估行为者网络产生的行为。由于评论 家的 价值 判断, 使得 评论 家难 以收敛,同 时行 为者 的更新,导 致了收敛更加困难。
1.3 深度确定性策略梯度算法
深度确定性策略梯度算法结合了深度强化学习算法和行为者评论家算法。行为者评论家算法中行为者网络通过调节参数θ确定状态下的最佳行为,评论家网络评估行为者网络产生的行为,结合深度强化学习之后,使用经验缓存,通过采样小批量的经验来训练行为者网络和评论家网络,另外还使用一个独立的行为者目标网络和评论家目标网络来计算损失。因此深度确定性策略梯度算法包含了4个神经网络,分别为:

行为者网络记为μ(s;θμ),以状态为输入,并产生行为,其中θμ为行为者网络的权重。评论家网络记为Q(s,a;θQ),以状态和行为为输入,并返回Q值a,其中θQ为评论家网络的权重。同理,行为者网络和评论家网络分别有一个目标网络μ(s;θμ′)和Q(s,a;θQ′),其中θμ′和θQ′分别为行为者目标网络和评论家目标网络的权重。
2 平衡控制算法
2.1 深度确定性策略梯度算法
DDPG算法的伪代码如算法1所示,其中步骤4中的循环如图3所示。
算法1:1)步骤1。初始化行为者和评论家的线上神经网络及参数: θQ和θμ;2)步骤2。将线上网络的参数复制给对应的目标网络参数:θQ′←θQ,θμ′←θμ;3)步骤3。初始化记忆库; 4)步骤4。对于每个回合,循环以下步骤:a.行为者网络根据动作策略选择一个at;b.智能体执行动作at,返回奖励值rt和新的状态st+1;c.行为者网络将(st,at,rt,st+1)存入记忆库中,作为训练线上网络的数据集;d.从记忆库中,随机采样N个训练数据,作为线上策略网络和Q网络的一个训练数据;e.计算线上Q网络的梯度;f.更新线上Q网络;g.计算策略网络的策略梯度;h.更新线上策略网络;i.软替换目标网络μ′和Q′;j.结束步循环。5)步骤5。结束回合循环。

2.2 算法实现
1)动作和状态。为了简化实验,仅训练了双轮机器人在0°位置的平衡。双轮机器人作为智能体,运动机构为直流减速电动机,直流减速电动机的电压决定了电动机转动的速度,实验中将5 V电压分为255份,动作的输入为0~255之间,单位时间为0.02 s。由于训练双轮机器人在0°位置的平衡,根据调试将动作的范围缩小到20~150之间。状态信息为MPU6050读取的x轴角度,读取的范围为-90°~90°之间,当x轴角度越大,双轮机器人的状态越不平稳,实验中将状态信息设置为-20°~20°之间。
2)奖赏。算法中提出了分层奖励,为了确保数据的准确性和减少训练次数,当状态在-10°~10°之间时,给与奖励,当超出此范围,奖励减5。

3 实验
3.1整体结构

双轮机器人的整体实物如图4 所示,双轮机器人的控制器采用了树莓派3 B+,电动机驱动器为树莓派3机器人扩展板Stepper Motor HAT,系统使用了Ubuntu16.04,传感器为MPU6050,驱动电动机采用了直流减速电动机。
3.2 算法参数设定
算法的参数设定对学习的效果起到至关重要的作用,其中学习速率体现了对于数据学习的快慢程度:学习速率太小会导致收敛过慢;而学习速率太大,则会导致代价函数振荡,无法收敛。实验中将行为者学习速率设定为0.1,评论家学习速率设定为0.2。
折扣因数取值为[0,1],学习效果不仅需要考虑当前的回报,还要考虑未来回报。实验中,将折扣因数设置为0.9。根据不同的参数带入实验和硬件的能力,设定的参数如表1所示。

表1 深度确定性策略梯度算法相关参数
3.3 训练过程
强化学习类算法在平衡车上应用的一大难点是智能体的训练,模拟仿真训练较为简单,且得到的数据准确,但是在实际训练智能体时,几万次的训练,一般很难做到,而且实验的数据并不一定准确。本文实验的训练环境如图5所示,将两轮机器人沿运动方向吊起,两边的倾斜角度为20°,此角度与设置的奖励角度留有余量,去除左右各10°的实验数据,保证了 实验 数据 的准 确性。另外 由于 设置 的角 度范 围较小,减小了实验的训练量,加快了实验的速度。

3.4 回转策略
实验过程中,新的状态与奖励传回算法中到算法给出新的动作耗时0.05 s,而在这个期间没有运动指令下,机器人根据惯性继续运动。当角度较小时惯性较小,延时性体现得并不明显,而当角度较大时,机器人往往会因为惯性较大的原因而摔倒。针对延时性的问题,实验中采用了回转策略,当新的状态和奖励传回算法中,控制机器人根据当前的状态信息继续往0°位置运动0.025 s再回转运动0.025 s。同时为了减小机器人的振荡,此期间机器人的运动速度采用了最小速度。
3.5 结果分析
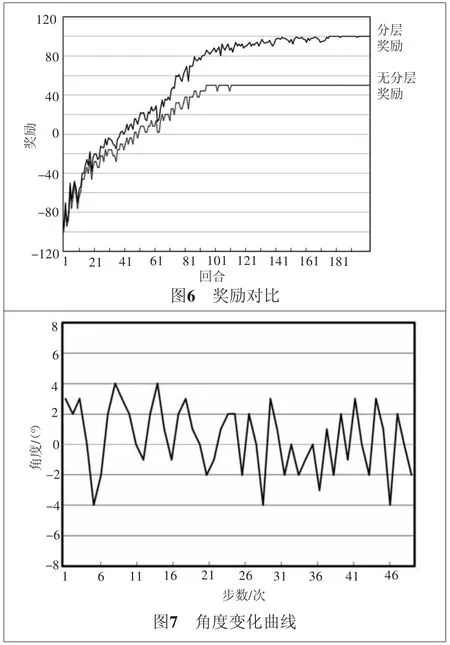
图6为双轮机器人未采用分层奖励和采用了分层奖励的情况对比。从图6中可以看出,采用了分层奖励策略可以清楚地看出机器人学习状态的变化,而未采用分层奖励策略的数据不能清楚地看出双轮机器人学习效率的大小。
在经过100回合之后的角度变化曲线如图7所示,由于回转策略的应用,双轮机器人的角度变化保持在-4°~4°之间。通过对上述实验数据的分析,在通过多回合的训练之后,DDPG算法有效地保持了双轮机器人的稳定。
4 结 语
本文针对深度强化学习在双轮机器人中的应用问题,提出了分层奖励和回转策略等方法。实验结果显示,双轮机器人的姿态角度波动范围在-4°~4°以内,双轮机器人能够保持直立平衡,证明了算法的有效性和分层奖励、回转策略的合理性,为解决深度强化学习在平衡控制提供了新的思路。
