一种上肢康复机器人机械臂的结构优化分析

柳海瑞， 王钰

（青岛大学，山东青岛266071）

0 引 言

在运动神经康复和关节肌肉的康复中，等速训练运动是不可缺少的一项关键环节[1]。目前市场上的上肢等速康复机器人均为单自由度运动，上肢的运动轨迹只能限于平面内，不能形成任意空间轨迹，使康复疗效受到限制，而且当上肢大角度伸展时，肩关节中心会随之升高，造成人机关节轴不对齐，进而给训练者带来附加约束力[2]。针对这些问题，本研究实现了一种两自由度等速运动，且能实时实现人机关节轴的动态对齐康复机器人结构，如图1所示。

由于自由度的增加及构型的要求，对运动臂的高刚性和低惯量提出了较高的要求，在设计上即是要限制某些方向上的变形量，同时实现结构的轻量优化。本文通过拓扑优化有限元法，对结构进行了轻量化设计，然后根据工作中的动态受力形式，对结构进行了谐响应分析[3]。与分析前的实物样机对比，有效减轻了运动部分的质量和转动惯量，同时改善了结构刚性和稳定性[4]。

1 上肢康复机器人的结构描述

图1所示的等速康复机器人由6个部分组成。垂直转轴和水平转轴的合成运动，代表肩关节两根正交轴的合成运动，使手臂末端走出一条空间轨迹。工作时水平臂板2、臂杆4、人机关节对齐机构5和水平转轴机构6是运动的，且臂杆4、人机关节对齐机构5和水平转轴机构6的重力均作用到水平臂板2上。已知运动部分的总质量为68.79 kg，质心坐标为（406.6 mm，305.5 mm，-0.3 mm）。

2 结构的设计要求

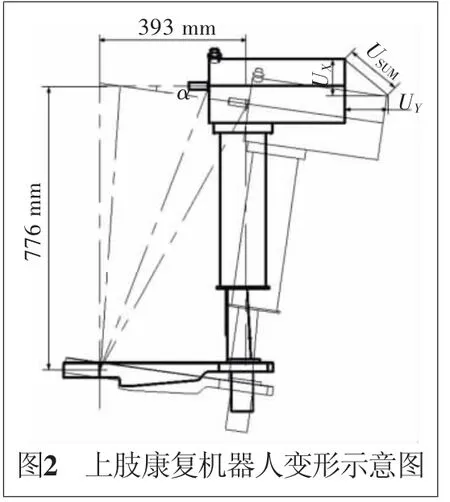
由于臂杆4的质量相较其他运动部分的质量小得较多，为简化计算过程将其忽略，其余运动部分的装配结构模型如图2所示。由于水平臂板呈悬臂梁状，首先对其静态下的挠度要有限制，如图3所示。设计上要求夹角α不能超过1°，根据平面几何关系可得α求解公式为

根据式（1）可以确定水平臂板的最大挠度值，以此建立轻量化的基本目标。

3 上肢康复机器人有限元分析

3.1 有限元模型的建立

本节为对康复机器人进行数值分析建立有限元模型，对实际结构进行几何清理和简化，并选取相应的单元类型，根据各个零件的连接状态选取不同的有限元装配技术。为了减少畸形单元的产生，将一些不受力的孔和窄边清理掉。其次，康复机器人上一些线圈、防护罩等零件对机器人的受力情况几乎没有影响，可以忽略不计。对于一些外购的标准件如减速器、传感器等零件，可以看成是一个整体，以减少不必要的装配关系，减少计算量。

将螺栓简化，以BEAM188单元代替螺杆，CERIG刚性区域代替螺帽与连接板之间的刚性区[5]。对于一些紧密接触的零件，由于始终不会分离，可以使用绑定接触来模拟零件之间的装配关系，由于水平臂板是本文主要的研究对象，其与垂直转轴机构之间的连接处的螺栓连接需要按照实际情况来分析。如图3所示，接触面1为绑定接触，接触面2为普通接触，螺栓中间施加预紧力单元，螺栓下端与垂直转轴机构之间通过刚性区域CERIG连接。

3.2 约束的创建与荷载的施加

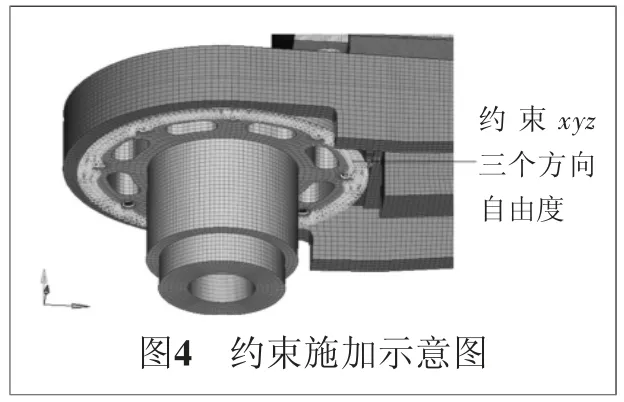
由于整个康复机器人都是通过水平臂板连接到机器人垂直转轴机构上，要重点分析水平臂板，因此只约束与水平臂板连接的结构即可，约束3个平动方向的自由度，如图4所示。

由试验得到康复机器人工作时患者施加在水平转轴机构上的最大力矩为26.29 N·m，根据臂杆的有效长度643 mm计算施加在水平转轴机构端部的力为40 N。患者运动频率一般可以达到4 Hz，极限状态可达到8 Hz左右。计算静力学分析时，仅计算机器人在重力作用下的变形和应力，施加一个全局重力加速度[6]。

3.3 上肢康复机器人静力学分析

本节对机器人进行静力学分析，观察康复机器人的力学性能是否可以满足要求，进而根据分析结果提出优化方案[7]。

将有限元模型导入ANSYS中，对整个康复机器人施加全局重力加速度，进行静力分析，在后处理器中观察康复机器人的分析结果，找到最大变形和最大应力，分别如图5和图6所示。由位移和应力云图可以看到，康复机器人的最大变形为0.50 mm，最大应力值为44.37 MPa，远远小于许可变形和应力。x方向位移为0.27 mm，y方向位移为0.46 mm，根据式（1）求出α为0.04°，满足α不超过1°的结构设计要求。

4 康复机器人的结构优化

4.1 结构的整体优化

对机器人进行减重处理，主要修改部分为人机关节对齐机构和水平臂板。为减少各连接板的装配，将原来的4块连接板改为2 块连接板。并将原来的丝杠改为选用小一型号的丝杠。由于机器人垂直转轴机构在运动时，水平臂板宽度过大可能会碰到患者的腿部，将水平臂板变窄，使用单梁支撑并加厚，水平臂板修改后模型如图7所示。

4.2 水平臂板的拓扑优化

4.2.1 拓扑优化设计

对修改后的水平臂板进行拓扑优化。采用OptiStruct 拓扑优化技术，材料模式采用密度法，即优化设计变量为设计空间的每个单元密度，单元密度按重要性从0～1连续取值，单元密度靠近0代表材料不重要，可以去除。

将约束部分（A部分）作为保留区域，以其他部分为优化设计空间，如图8所示，本次目标优化问题是目标体积最小化，约束则是水平臂板右侧的节点2 212 305的位移0.25 mm。

4.2.2 优化分析结果

查看密度结果等值面图如图9所示，红色部分密度接近于1，保留；蓝色区域密度接近于0，取优化阈值为0.25，最优化布局等值面图如图10所示。

根据最优化等值面图对水平臂板进行结构设计。如图11所示，将水平臂板左端的边沿减薄，应力集中部分加厚，将中间肋板掏空，将右端的连接部分减薄。

4.3 优化前后康复机器人动静态性能对比

对优化后的康复机器人进行静力分析，并与优化之前结构对比，结果如表1所示。由表格数据可以看到，优化之后的模型，质量减轻了38.8 %，变形和应力都有减小，且康复机器人绕转轴中心的3 个方向的转动惯量明显减小。

表1 优化前后对比结果

5 结 语

本文对上肢康复机器人进行静力学分析和谐响应分析，计算出其在自身重力和工作时的变形与应力。并根据分析结果，对康复机器人进行结构优化设计。通过对主要受力零件水平臂板进行拓扑优化设计，优化后的康复机器人质量明显减轻，且力学性能有很大提高。本文针对结构设计所采用的研究方法，同样适用于其他类似结构的设计与分析。