基于频率变化平方比的压力管道损伤定位方法探究

2020-03-27郑尚书高彩玲梁博

中国设备工程 2020年3期

郑尚书，高彩玲，梁博

（西安特种设备检验检测院，陕西西安 710065）

压力管道在工业制造与生产中是非常普遍的素材，尤其是化工、石油与食品行业。经过生产实践发现，压力管道检测过程中存在超标的问题，必须紧急组织检测，总结缺陷根本原因、位置与解决方案，为后期修复提供参考。通过文献与理论研究发现，断裂力学评定法、失效载荷评定法是压力管道损伤的有效方法，针对压力容器、机械设备展开无损检测时，往往是以超声波探伤、磁场探伤和工业X 射线探伤这几种技术为主，尽管在各个领域的应用已经非常普遍，但是对比振动损伤检测法，后者在信号提取、探测器安装等方面有着非常明显的优势。分析可以确定，该检测方法是在频率变化平方比的基础上运行，下面便以此为前提分析压力管道损伤定位的有效方法。

1 压力管道损伤与检测方式

常用的压力管道检验方法是以工业管道定期检验规范为依据，在明确地检测规范、方式、比例、管道级别等的要求下，也扩大了压力管道检验方法的适用范围。然而，因为待检测管道的实际情况存在差异，根据规范组织检测有可能引发检验针对性差、检验过度等问题。根据压力管道定期检验要求，一些成套装置压力管道，建议采用风险检验的方法。但是，这种检验方法对检验机构专业性、实际应用管理水平有非常高的要求，加之压力管道本身具有特殊性，无法快速判断是否为成套装置。另外，需要注意的是，如果DCS 控制系统缺失，使用该技术进行检测也存在一定的难度。所以，在实施压力管道损伤检测时，需要和检验机构达成一致，根据常规检验要求，提前判断管道损伤模式，并且结合损伤基本形态、损伤高发部位与检测方法，制定内容完善的检验规划。

2 基于频率变化平方比的压力管道损伤定位方法原理

以频率变化平方比为前提的压力管道损伤定位，如果不考虑阻尼带来的影响，可以得出结构振动特征值方程式：（K-ω2M）φ=0（1）。该公式中的K 代表结构整体刚度阵，M 代表结构整体质量阵，φ 代表正则化振型，而ω 则表示固有频率。这里提到的结构损伤，一般会引发质量阵、刚度阵改变，这时φ、ω 也会出现变化量。针对压力管道这一类大规模的工程结构，定位损伤时需要降低结构刚度，质量分布不会受到较大的影响。鉴于此，结构动力方程式也可以转变为：[（K+△K）-（ω2-△ω2）M]=（φ+△φ）=0 （2）

针对公式（2）进行整理，可以将二阶项忽略，得出公式：

针对其中的一个阶模态i，整理公式（3）得出：

针对公式（4）进行单元变形，依据结构振型计算，得出：

公式（5）中的εm 表示单元变形，整理之后得到：

该公式中的Q 表示结构单元总数，针对单一的单元N 可以将公式（4）转变为：

（7）

该公式与公式（4）对比，是将单元属性、结构频率的改变有效连接。因为结构单元变形从振型中得出，当损伤发生于其中一个阶振型当中，并且成分占比较大，方可对频率变化带来明显的影响。

3 压力管道损伤定位

3.1 损伤判断

通过公式（7）可以发现单元刚度矩阵与频率两种变化的必然联系，这时可以确定单元损伤系数的表达式：

该公式中的αN=Tij代表的是损伤系数矩阵，如果将公式（9）代入到（7）当中，可以得到：

一般在判断损伤时，公式（10）的αN为损伤单元常数，被称作损伤因子，经过整理之后可以将公式（10）转化为：

式（11）中将特征值变化在单元损伤程度、位置上的依赖性真实的表示出来，因为结构中的任一阶模态所表现的“频率变化平方”，所包括的单元损伤程度数据一致，通过i、j这两个振动模态便可以获得i 阶、j 阶频率损伤之后发生变化的频率变化平方比，从而证明其与损伤单元位置相关。最后再通过公式（12）定位结构中的损伤。

3.2 实际应用

某厂在压力管道生产与设计时，所使用的钢管长度为250cm，技术人员分析发现钢管存在轴向振动。测量得到该钢管的内外径分别是35mm、50mm，生产过程中，0.550 ～0.680m 与1.450 ～1.660m 这两个位置出现损伤。0.550 ～0.680m 处的损伤圆心角是30°，另外一处损伤的圆心角则是15°。随后展开有限元计算，将损伤部分划分为均等的10 个单元，压力管道结构如图1 所示。

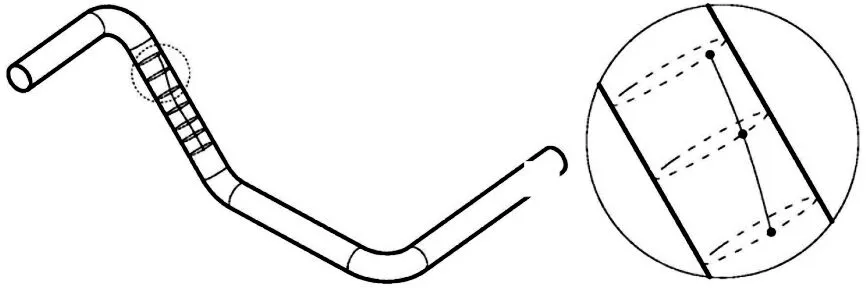
图1 压力管道结构图

根据上述理论进行推导，结构损伤所在位置，推导流程如下：第一，压力管道接受有限元模拟，管道损伤之前与之后分别展开动力分析，获得频率、振型基础数据。如果管道是因为损伤而发生自振频率的变化，可以将获得的各阶频率制成频率变化平方比。本次试验主要包括3 根压力管道，1 号管道未损伤之前的自振频率是12735680，损伤之后的自振频率是12256470，2 号管道未损伤之前的自振频率是112744660，损伤之后的自振频率是110085200，3 号管道未损伤之前的自振频率是3029732650，损伤之后的自振频率是，2609100。通过数据对比，发现模拟管道0.550 ～0.680m 与1.450 ～1.660m 这两个位置发生损伤之后，管道的前5 阶特征值和原本管道特征值进行对比，可以得出管道受损之后的频率变化平方比。随后再对比所有计算值，按照现有数据，结合振动阶次便可以绘制直方图，观察结构损伤位置。

第二，根据公式（12）对划分的10 个单元管道损伤之后的频率变化平方比进行计算，并且结合振动阶次，对比各个单元计算值，发现其中有几个单元相同。考虑到结构性质，主要通过结构单元信息将其表述。因此，0.550 ～0.680m 与1.450 ～1.660m 两个位置可以确定为损伤单元。采用以上方式判断管道损伤，并且实施检测可以获得明显的成效，最终结果和损伤位置的关系非常密切，根据频率变化平方比绘制直方图，验证压力管道损伤定位结果。

3.3 结论建议

第一，通过结构振型、频率判断结构中是否存在损伤，在实际应用中有非常直观的成效，且这种方法的操作流程比较简单，最终得出的结果准确率高；第二，压力管道结构的频率变化平方比中，涉及到大量结构损伤程度、位置数据，经过理论分析之后发现频率变化平方比只是和结构损伤位置有比较密切的关系，所以可以将其用在损伤定位中；第三，以上分析中是以的理论计算方式，如果将其用在管道的有限元损伤模拟计算环节，能够准确识别一些比较细小的损伤，如果在工程领域运用，因为测试模态振型有非常高的噪声水平，所以最终实际测量的频率、振型无法保证准确性，这便会对损伤识别结果造成影响。如果压力管道的局部刚度损伤规模不大，需要在实践操作中探索有效的判定方法。