基于等效电路图的锂离子电池SOC 估计及卡尔曼滤波器应用方法

毕福亮

（中车长春轨道客车股份有限公司，吉林 长春 130062）

电池电荷状态（SOC）检测是电池管理系统（BMS）的主要任务之一。目前，安培计数方法被认为是最精确的SOC 估计方法，但它需要一些条件，如初始SOC 值，以及常规的完全充电或充电。在一些应用中，这些条件并不总是满足，因此，由于测量误差累积，不能直接从电流测量进行SOC 计算。对此，可以通过使用数学模型来估计SOC 以表示电池的动态特性。卡尔曼滤波器本质上是实现预测——校正估计器的递归数学方程。它基于输入控制和输出测量来生成系统状态的最佳估计，因此，主要用于无法直接测量系统状态，且需要从输出测量中得到最佳估计。本文首先介绍了离散卡尔曼滤波器和扩展卡尔曼滤波器（EKF），最后，对锂离子电池的状态空间建模。此外，对比了安培计数和EKF 两方法所得的SOC。

1 卡尔曼滤波器

卡尔曼滤波通常用于估计一个用线性随机差分方程描述的离散过程的状态变量，该模型原理及离散过程在文献[5]中已有详细的介绍说明。然而，如果被估计过程和（或）观测变量与这个过程的关系都为非线性时，直接使用卡尔曼滤波是不能处理这些情况的。将期望和协方差线性化的卡尔曼滤波称为扩展卡尔曼滤波(EKF)，它是解决非线性滤波问题经常使用的方法，其详细介绍在文献[6]中有说明。

2 电池空间状态模型

2.1 电池模型

本文运用了基于等效电路图建立了两种电池模型。第一个模型为“一阶常数模型（OTC）”，如图1a 所示。它由电压源Voc，电阻0R， ROTC和电容 COTC组成。 vOTC是 COTC的电压； iOTC是流入 COTC的电流。OTC 模型的电性能在离散时间内可表示为：

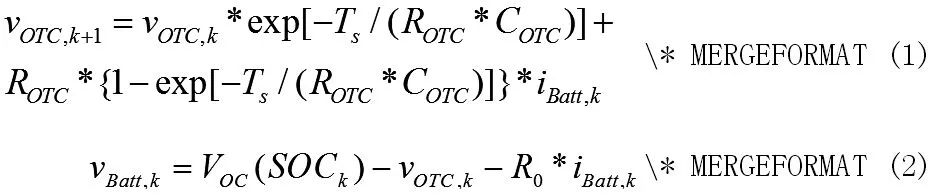
第二种模型称为“二阶常数模型（TTC）”，如图1.b 所示，它由四部分组成：电压源Voc，电阻 0R， RTTC1和电容 CTTC1用来描述短期特征， RTTC2和 CTTC2描述长期特征。 vTTC1和 vTTC2分别是 CTTC1和 CTTC2的电压。 iTTC1和 iTTC2分别是流出 CTTC1和的电流。TTC 电路的电气特性在离散时间内表示与式（1）、（2）相似，在此不赘述。

图1 电池等效电路

2.2 OTC 模型空间状态

Sk是SOC 在第k 步的缩写，由下式定义：

其中，T 是采样时间，η 是库仑效率，CN是电池标称容量。

通过代入，OTC模型的离散时间状态空间形式如（4）（5）所示：

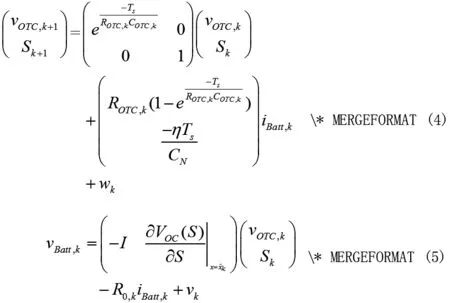
2.3 TTC 模型状态矩阵

TTC 模型的离散时间状态空间如下。

。

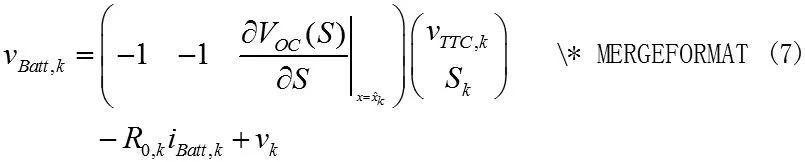
3 实验和计算结果

3.1 自适应模型参数的SOC 估计

通过使用具有自适应模型参数的扩展卡尔曼滤波器来完成SOC 估计。在估计期间，参数值随着每一时间步的变化作为SOC 的函数。实验运用了线性插值进行参数计算。图2 显示了与安培计数结果相比，模型OTC 和TTC 的SOC 估计结果。由该图可知，三种SOC 的曲线大致相同。

由EKF 估算的OTC 和TTC 模型的SOC 值与通过安培计数法计算的SOC 值之间的百分比误差如图3 所示。它表明，使用TTC 模型的SOC 估计比使用OTC 模型更准确（参见图3，8 小时后）。与OTC 相比，TTC 模型的绝对平均误差减少了约20%，绝对最大误差减少约3 倍。因此，TTC 模型比OTC 模型能更准确地描述锂离子电池。

3.2 不同初始值下的SOC 估计

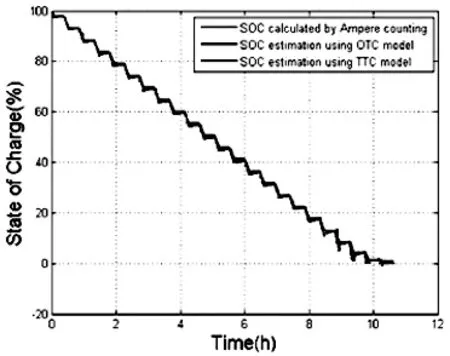
图2 比较EKF 和安培计术法用于OTC、TTC 模型的电池SOC 估计

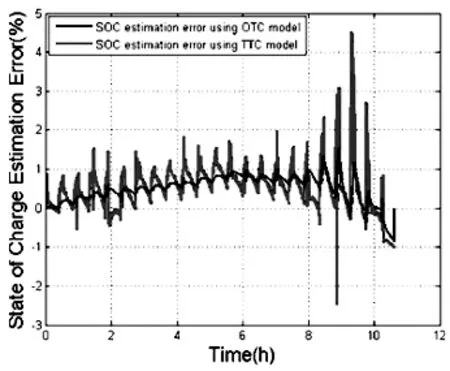
图3 OTC 与TTC 模型的SOC 估算百分比误差

由式（2）、（3）可看出，准确的SOC 估计取决于两个方面。一是SOC 初始值，二是计算方法。为了研究SOC 估计如何受SOC 初始值的影响，以电池容量90%作为SOC 初始值，用EKF 法对OTC 对TTC 两种模型进行SOC 估计，结果如图4 所示。它表明了该方法一开始会有误差，但很快收到实际SOC 值。

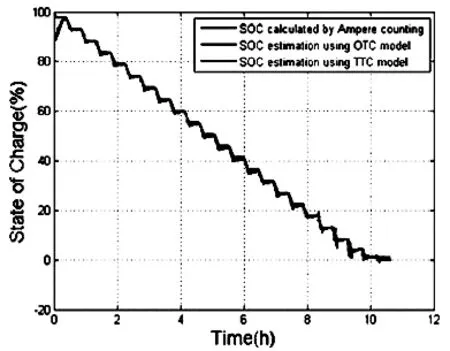
图4 SOC 初始值为电池容量90%时，EKF 法对OTC 对TTC进行SOC 估计

4 结语

本文介绍了扩展卡尔曼滤波器在锂离子电池上的应用，为获得最佳的SOC 估算，应用了卡尔曼滤波器及其扩展滤波器。本文比较了安培计数方法与EKF 两种方法用于SOC 估计结果。结果表明，TTC 模型有着更高的SOC 估计精度，且错误的初始值几乎不影响SOC 估计。最后，该算法将用于在线SOC 估计的硬件实现。