基于下垂控制的低压微网控制策略

陈 莹，义 琦

（广西大学 行健文理学院，广西 南宁 530000）

0 引 言

微电网是建立在用户侧附近的小型发电系统[1]。由于线路电压等级的不同，线路阻抗所呈现的阻感性也不相同[2]。本文根据低压输电线路的特性，提出适用于低压微网的下垂控制方法，并通过MATLAB软件仿真。

1 低压微电网的结构与线路阻抗

以光储作为发电单元为例，微网主要包含发电单元、逆变单元、负载以及电网电源4个部分[3]。逆变单元一般靠近发电单元安放，从逆变单元到用户侧交流母线的电压等级不同，线路阻抗的阻感性也不相同[4]。典型线路阻抗如表1所示，其中X为感抗值，R为阻抗值，X/R为阻抗比。

表1 典型线路阻抗

对于微电网而言，发电单元往往建立在距离用户较近的地方，传输线路一般为低压线路，线路阻抗与传统大电网不同，因此不可直接套用传统大电网的下垂控制方法[5,6]。

2 控制策略

两个光伏分布式电源并联发电的微网结构如图1所示。其中，DG1和DG2为光伏发电单元，通过光伏逆变器转换为三相交流电，传输到交流母线后供给负载。

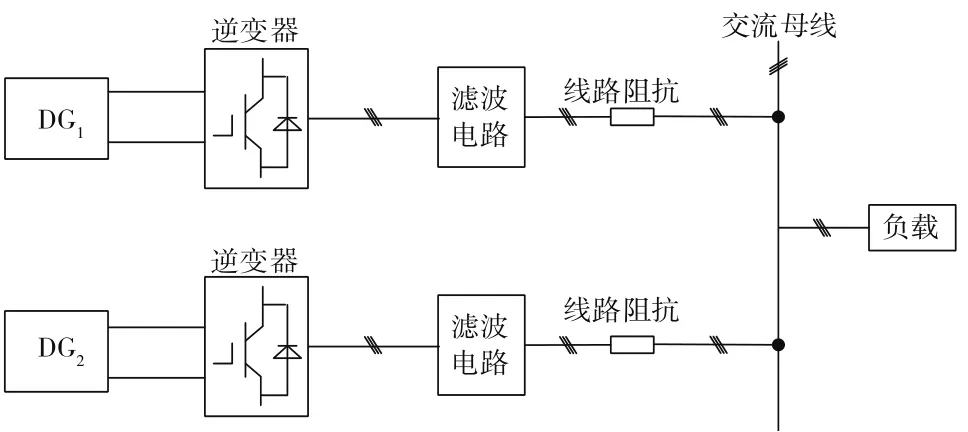
图1 微网结构示意图

经化简，得到该微网模型的等效电路图如图2所示。其中，E∠0为交流母线上的电压；Un∠δn为逆变器n的输出电压，n=1,2；Z1∠θ1为负载阻抗；Zn∠θn为逆变器n的线路阻抗，n=1,2[7]。

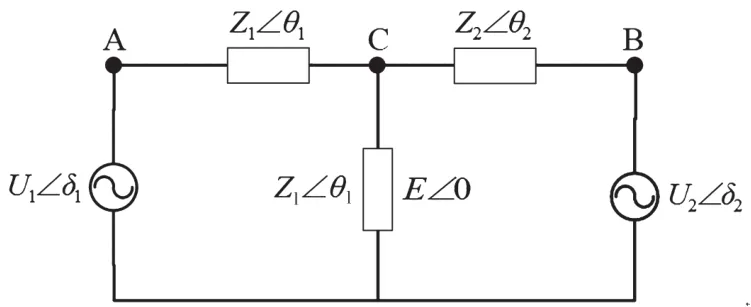
图2 光伏逆变器并联运行等效电路图

A点处的视在功率为：

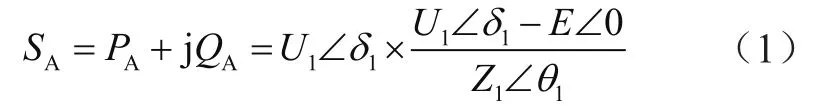
根据式（1）可求得A点处的有功功率PA和无功功率QA为别为：

在逆变器的作用下，C点处功率为：

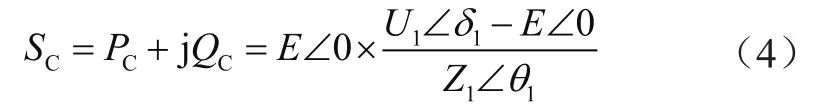
求得对应的有功功率PC和无功功率QC分别为：

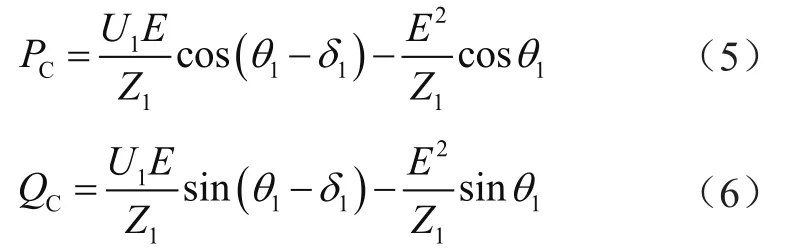
由此可得PCC节点处功率与逆变器输出电压的幅值相角之间的关系，其中相角通常用频率f代替相角并带入计算[8]。

由于传统分布式电源都是远距离高压输送电能，因此输出线路阻抗呈感性[9]。线路阻抗角θ≈90°，此时PCC节点处的功率为：

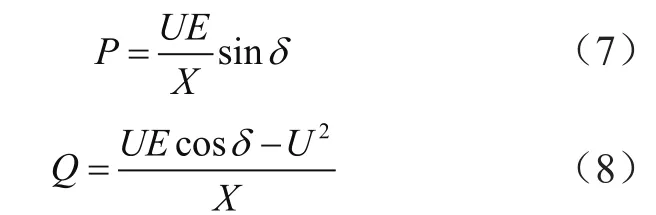
传统下垂控制方法为：

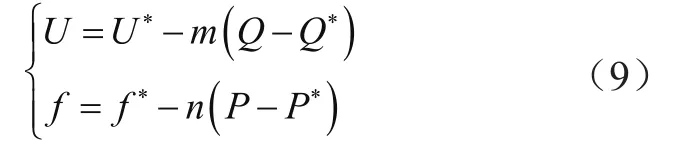
式中，U和U*分别为逆变器输出电压幅值的参考值和额定值；f和f*分别为逆变器输出频率的参考值和额定值；P和P*分别为逆变器输出有功功率的参考值和额定值；Q和Q*分别为逆变器输出无功功率的参考值和额定值；m和n分别为有功功率和无功功率对应的下垂控制系数。

微电网一般建立在用户侧附近，采用中低压输送电能，因此输出电路阻抗呈阻感性。若直接采用传统下垂控制方法控制逆变器输出，那么会由于受线路阻抗中的阻性部分影响，输出效果较差。

光伏微网一般通过低压传输线路接入用户侧，线路阻抗的感性很小[10]。若线路阻抗角θ≈0°，此时PCC节点处的功率为：

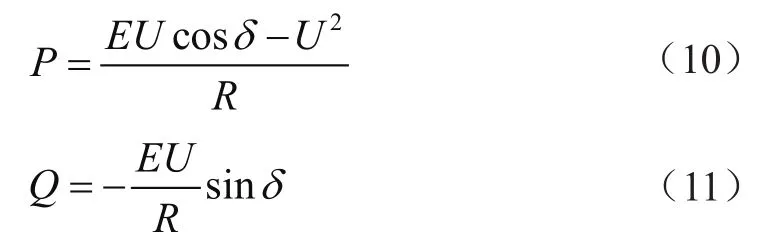
此时，下垂控制方法应改为：

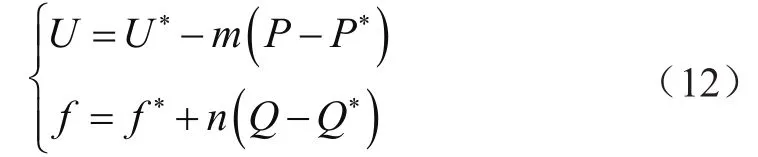
虽然阻抗中感性部分所占比例较小，但依然会引起逆变器输出在传输过程中产生不小的偏差。

下垂控制方法实际上是通过检测逆变器输出的功率变化来判断负载的需求，而在传输过程中由于线路阻抗的干扰，阻性线路阻抗和感性线路阻抗对下垂控制调节的影响并不相同。本文将线路阻抗等效化为纯阻性和纯感性两个部分进行分析，并结合纯感性线路情况下的下垂控制方法和纯阻性线路阻抗情况下的下垂控制方法提出改进后的下垂控制方法。

单个微源供电的线路阻抗等效电路如图3所示。将线路阻抗Z∠θ等效拆分为两个部分，分别是阻性阻抗R和感性阻抗jωL，设两者之间的电势设为U′∠δ′，该处有功功率和无功功率分别为P′和Q′。

图3 线路阻抗等效电路图

当负载发生变化时，通过式（12）的下垂控制方法克服线路阻抗R所产生的影响，使U′∠δ′跟随对于控制律变化。U′∠δ′输出的电压幅值增量ΔUR和频率增量ΔfR分别为：

式中，m1和n1分别为克服阻性线路阻抗时电压和频率对应的下垂控制系数。

再用式（9）的下垂控制方法令U∠δ随U′∠δ′的变化而变化。U∠δ输出的电压幅值增量ΔUL和频率增量ΔfL分别为：

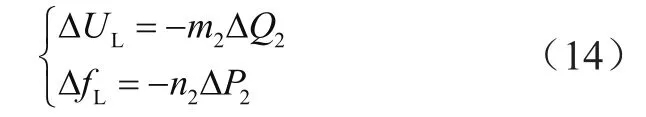
式中，ΔP2=P-P′；ΔQ2=Q-Q′；m2和n2分别为电压和频率对应的下垂系数。

设U′∠δ′处功率P′、Q′与逆变器输出功率P、Q的关系为：

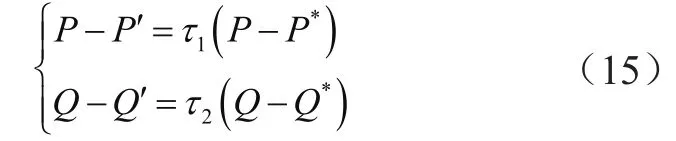
将线路阻抗看做感性部分先单独作用，再由阻性部分单独作用。即将感性部分作用后所产生的电压幅值增量ΔUL和频率增量ΔfL嵌入式（12）控制方法中，以克服感性部分线路阻抗的影响，得新的下垂控制方程为：

令m1=m，τ2m1m2=m′，τ1n1n2=n，n1=n′。式（16）可化简为：

式中，m和m′是电压幅值下垂系数；n和n′是电压频率下垂系数。

根据式（18）改进下垂控制方法，在MATLAB软件中搭建该模型，如图4所示。

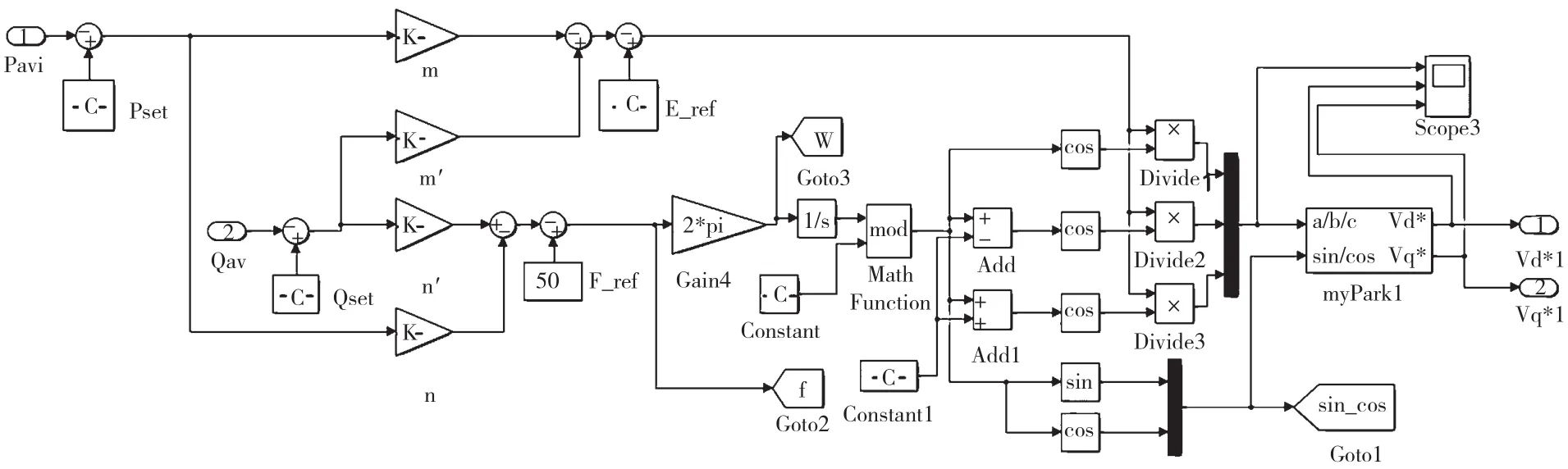
图4 改进后的下垂控制模型

3 模型仿真

模拟在距离用户侧PCC节点线路长度为1 000 m处安装光伏微源DG1，其额定输出电压的幅值为403 V，频率为50 Hz。额定情况下，输出有功功率为2 127 W，无功功率为2 400 Var。经估算，线路阻抗约为（0.642+j0.083）Ω。配置系统模型对应参数，进行投切实验。

3.1 引入传统下垂控制方法

由于低压线路阻抗角约为7.366 5°，阻抗角较小，因此可近似认为线路阻抗为纯阻性。利用对应线路阻抗为纯阻性情况下的下垂控制方法进行仿真实验。根据式（12）在MATLAB软件平台上搭建出对应线路阻抗为纯阻性情况下的下垂控制模型如图5所示。

图5 下垂控制模型（纯阻性）

其中，下垂控制系数m=0.68，n=0.000 16，逆变器输出限幅403 V。在0 s时，将负载设置为P=2 100 W，Q=1 300 Var，3 s时，切断700 Var无功负载，6 s时，切断1 500 W有功负载。投切实验仿真结果如图6所示。

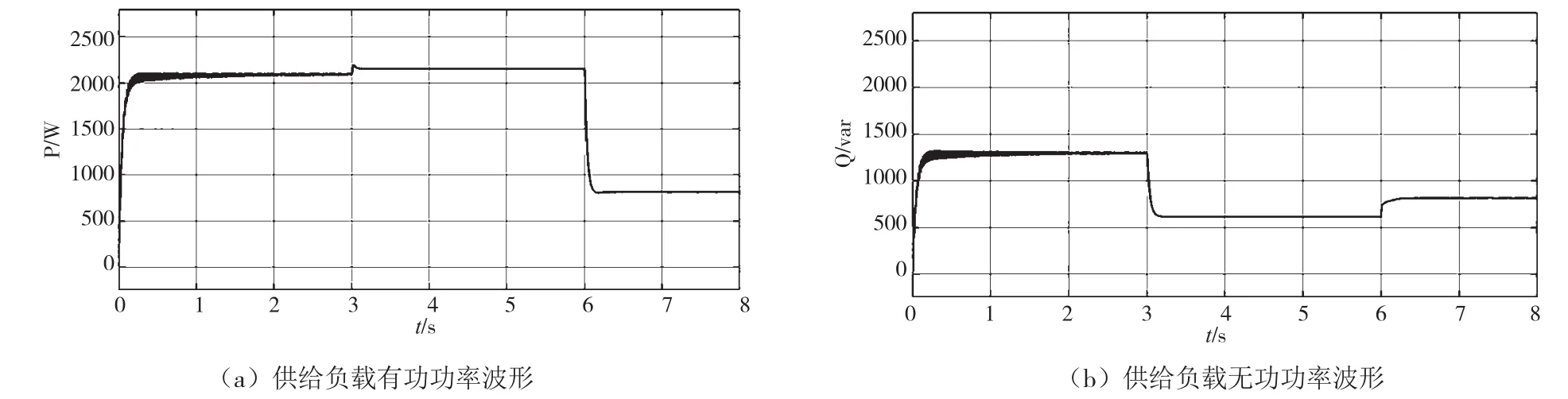
图6 引入下垂控制方法（纯阻性）后，供给负载功率波形

由仿真结果可知，当负载发生变化时，逆变器供给负载的功率随之变化，但受到线路阻抗的影响，调节后系统功率的供需关系存在明显误差。其原因主要是线路阻抗中感性部分不受控，引起的误差。

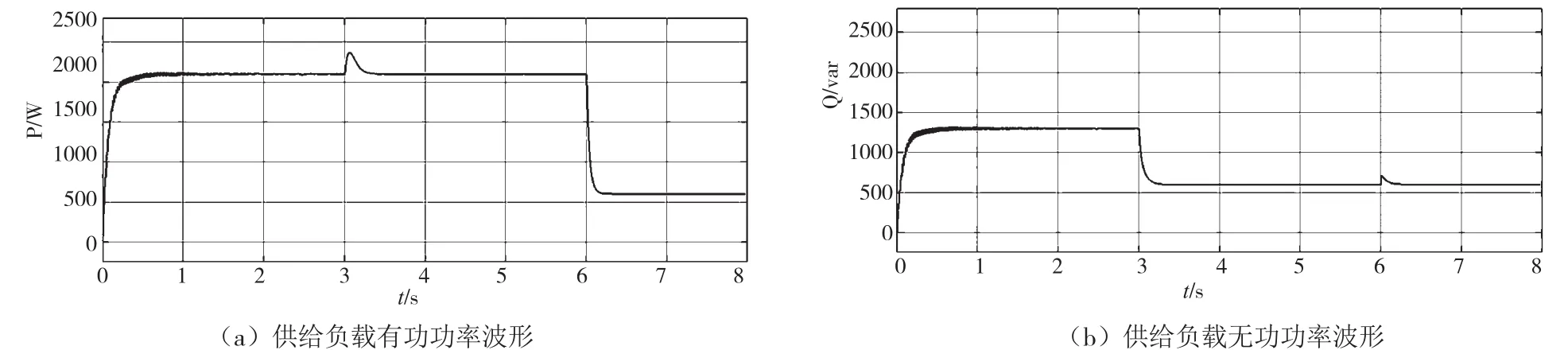
图7 改进下垂控制后，供给负载功率波形图

3.2 引入改进下垂控制方法

为了解决线路阻抗中感性部分不受控这一问题，用改进后的下垂控制方法代替纯阻性线路阻抗对应的下垂控制方法，进行相同的投切实验。配置各项下垂控制系数m=0.006 8，n=0.000 17，m′=0.039 8，n′=0.000 16。仿真结果如图8所示。

由图7可知，在3 s时，负载需求的无功功率下降，系统供给负载功率发生突变，新的下垂控制律能迅速做出调节，并将供给负载的功率调节至供需匹配，在6 s时，突然切除部分有功负载，系统能快速检测到并做出调节，使功率的功率关系回归稳定。

实验结果表明，改进后的下垂控制方法对比纯阻性线路阻抗对应的下垂控制方法，能克服线路阻抗中感性部分的影响，使系统调节更精确。改进后的下垂控制不但提高了系统的供给准确度，还提高了系统的鲁棒性。