储能变流器孤岛模式下控制策略研究
2020-03-27黄日帆范丽波
王 鹏,黄日帆,高 帅,2,范丽波,2
(1.许昌学院 国际教育学院,河南 许昌 461000;2.华北水利水电大学 电力学院,河南 郑州 450000;3.广西科技师范学院 机械与电气工程学院,广西 来宾 546100)
0 引 言
20世纪90年代,以Dewan S B、Wu R为代表的科研人员较为全面地分析了三相变流器的时域数学模型,建立了低频和高频模型[1]。Dong Y H和Chun T R等人提出对变流器进行dq旋转坐标变换,并建立了低频的变流器等效电路模型[2]。
按拓扑结构,储能变流器可分为AC/DC型储能变流器和DC/DC-AC/DC型储能变流器[3-5]。AC/DC型储能变流器具有结构简单、控制策略容易实现以及运行效率高等特点。在结构上,DC/DC-AC/DC型储能变流器比AC/DC型储能变流器多一个DC/DC直流变换环节。DC/DC-AC/DC型储能变流器的器件较多,导致其效率低下,且需要充分考虑DC/DC变流环节和AC/DC变流环节的协调控制,控制方法复杂[3-6]。隔离变压器可以实现电压和电流的变比,同时能够有效隔离系统一次侧和二次侧的电气,在电网发生故障时能对储能变流系统起到关键的保护作用,以有效减少损失[7,8]。变压器隔离一般分为工频变压器隔离和高频变压器隔离两种。工频隔离变压器具有结构简单、体积大、效率低以及故障率较低等特点。高频变压器的特点是体积小、噪音低以及效率高,应用范围广泛,能有效提高储能变流器的功率密度。
在控制算法方面,为实现变流器网侧电流正弦化和单位功率因数运行,科研人员将脉宽调制(Pulse Width Modulation,PWM)技术引入变流器[9]。基于PWM技术的控制技术研究具有重要的现实意义,符合我国建设资源节约型社会发展的需要。
本文主要针对储能变流器在孤岛模式下的控制策略进行研究,建立了储能变流器的孤岛恒压恒频工作模式,并设计了相应的控制策略。通过搭建MATLAB仿真模型,验证了系统的稳定性,并为后续储能变流器系统在结合电网、光伏与负载不同情况下的应用提供了理论支撑。
1 控制结构
根据储能变流器的孤岛模式工作方式,给出孤岛控制结构框图,如图1所示。当储能系统脱离电网运行时,三相交流母线失去了公共电网电压和频率支撑。首先设定的系统工作频率为fref,本文选定fref=50 Hz。系统的角速度为2πfref=100πrad/s,通过系统角度积分得到相角θ作为系统输出电压相位。给定有功电压分量Vdref与无功电压分量Vqref指令,通过电压、电流双环控制器控制变流器输出电压幅值和相位。将Park反变换后的电压信号U*通过SVPWM调制输出驱动脉冲来驱动开关管,以获得所需的理想电压。

图1 孤岛模式控制结构图
2 控制器设计
2.1 功率控制器设计
将电网电压、电流变换到同步旋转坐标下,得到Vd和id以及储能变流器实时功率P和Q:

本文采用电网电压矢量定向的方式,锁相环输出Vd与d轴重合,有Vd=0,则式(1)表示为:

在电网电压矢量被锁相环精确锁相的条件下,储能变流器输出的有功P、无功Q分量只与同步坐标系下的电流id、iq有关。通过控制id、iq,可以实现电网对有功、无功的独立控制。通过式(2)求出电流环给定电流iq、id的大小为:
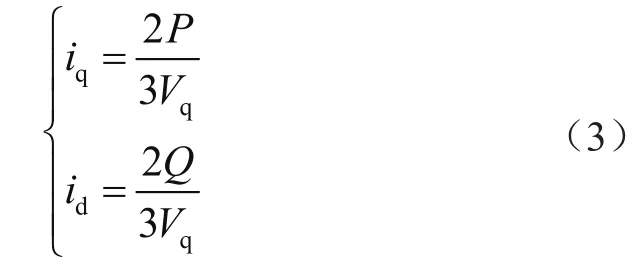
2.2 电流环控制器设计
对两相旋转坐标系下的d轴和q轴分量进行解耦,变流器在两相dq旋转坐标系下的数学模型为:
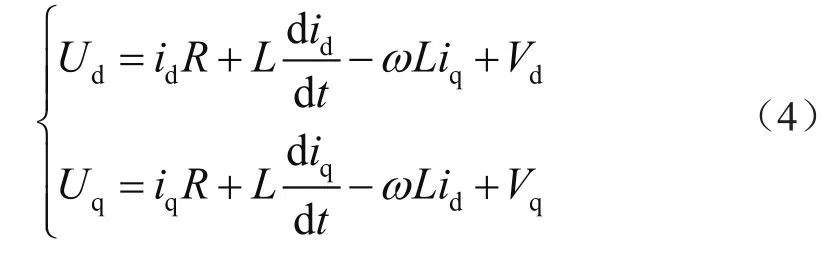
式中,dq旋转坐标系下的d轴、q轴分量处于耦合状态。控制器的设计相对复杂,首先要进行PQ解耦,即:

式中,KiP和KiI分别为电流PI调节器的比例系数和积分系数;id*和iq*为dq坐标系下d轴和q轴电流的给定值。当旋转坐标系d轴和电网电动势矢量一致,有d轴分量Ud=Uq,则q轴的分量Uq=0。
通过电流内环的解耦,实现有功分量和无功分量的单独控制。考虑电流环的对称性,详细分析d轴的电流环设计,分析计算出PI调节器参数。解耦后的id电流内环控制框图如图2所示。

图2 id电流环控制结构框图
在理想状态下,Ud扰动量忽略不计,KPWM为变流桥路的等效放大系数,值等于1。PI调节器积分时间常数用τi表示,电流内环电流采样周期用Ti表示,流内环信号采样延迟用1/(1+Tis)表示,PWM控制的小惯性环节用KPWM/(1+0.5Tis)表示。
本文按典型Ⅰ系统原则设计电流环[10]。取τi=L/R,抵消开环传递函数的零点与极点。对结构图中的小时间常数进行整理合并,根据电流闭环结构图可知其开环传递函数Go(s)为:

将PI调节器的传递函数GPI(s)写成零极点形式:

式中,KiI=KiP/τi。加入PI调节器,采用零极点对消法,加入补偿环节,系统开环传递函数数Goc(s)为:

式中,T1=1.5Ti;K1=KPWMKiP/R。由Ⅰ型系统的二阶最佳整定法,将其与典型Ⅰ型系统开环传递函数标准式进行比较,此时ξ=0.707[10]。可得:

根据式(9),得:

式(10)中,根据设计要求带入数值即可求出电流内环PI调节器的比例系数KiP和积分系数参数KiI。
2.3 电压环控制器设计
直流电压环主要用于控制变流器直流侧电压稳定,实现对储能电池恒压充电。该模式下,电流环为电压外环的一个传递函数。当储能变流器运行于单位功率因数时,由交直流侧能量守恒原理,可得交流侧电流idc与直流侧电流Im的关系为:

式中,PWM调制度m≤1;θ为初始相位角度。系统电压外环的控制结构如图3所示,Tv表示直流电压外环的采样时间常数,其中KvI+TvKvPs/Tvs表示PI环节。电压外环对直流侧电压进行控制,具有稳定直流侧母线电容电压的作用。同时,电压外环的输出值将作为电流内环的给定值。电压外环的截止频率较低,时间常数较大。对电压外环来说,电流内环的采样时间Ti很小,因此可忽略传递函数二次项,将其简化为一个简单的惯性环节。

图3 电压环控制结构图
电流内环作为电压环的传递函数Gic(s),表示如下:

当m=1、cosθ=1时,设计最复杂,此时设计的电压控制器在任何情况都能达到控制系统需求。
因为1/(1+Tvs)为电压外环信号采样的延时环节,1/(1+3Tis)为电流闭环传递函数,其中Tv和Gci(s)中的3Ti都是小惯性时间常数,所以可以将这两项合并,得到新的传递函数Gov(s)为:

忽略iL的影响,简化电压环控制结构,如图4所示。

图4 简化的电压环控制结构
电压环控制的目的是稳定变流器直流侧电压,以满足储能变流器对储能电池进行恒压充电。考虑到电压外环的抗干扰性,按典型Ⅱ型系统设计电压PI调节器。
电压环的开环传递函数Kvi为:

由此得电压环中频宽hv为:

根据典型Ⅱ型系统控制器参数整定原则,可知:

由式(15)~式(17)可得电压控制器PI参数设计公式:

式(17)为直流电压环PI参数计算公式,在工程调试时进行适当修改,可得到一组最合适的PI参数。
3 仿真分析
在MATLAB/simulink中搭建三相储能变流器仿真模型,通过仿真分析验证系统在孤岛模式下的运行控制原理及其控制策略。整体仿真模型如图5所示。
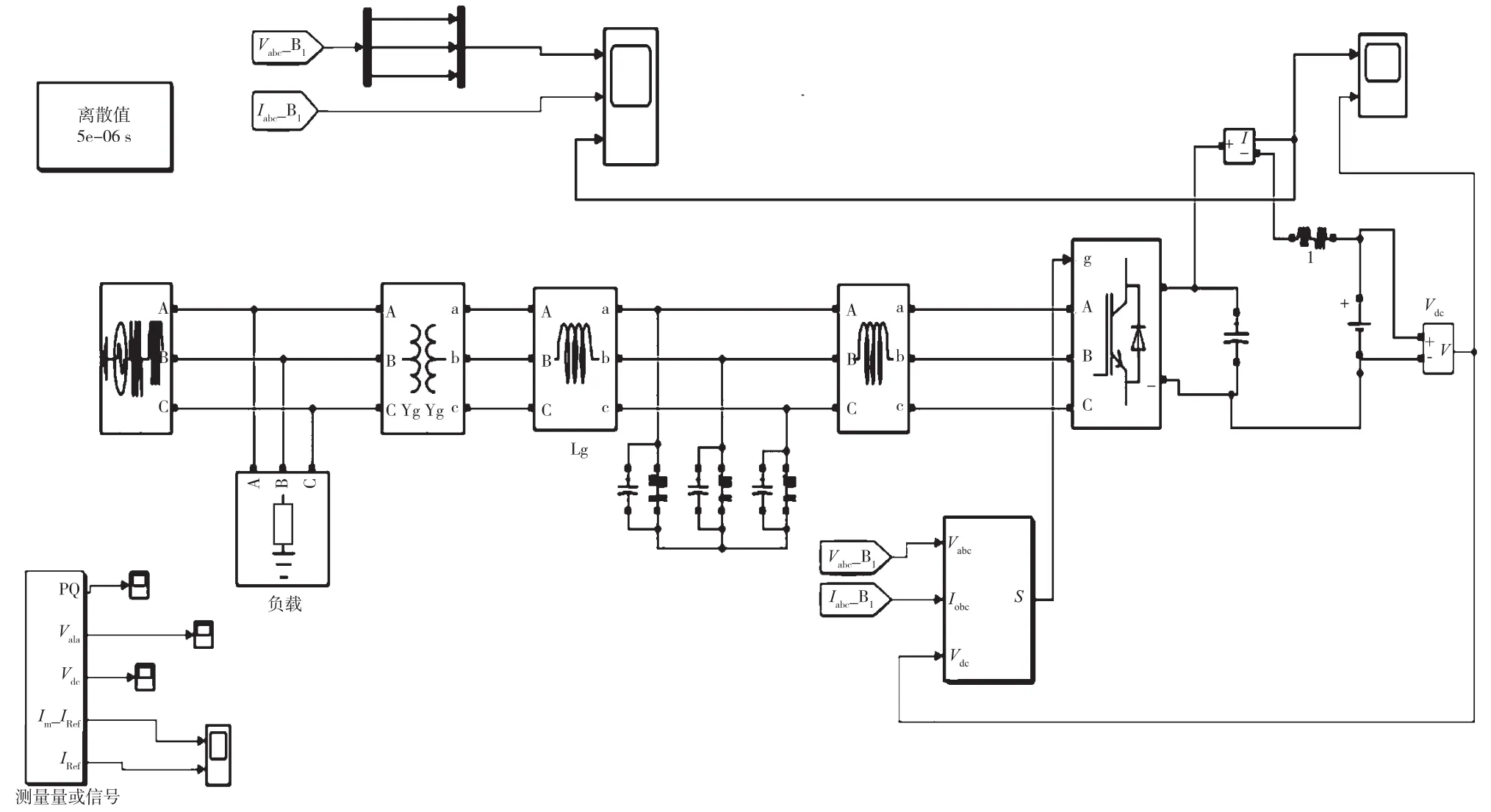
图5 储能变流器仿真模型
仿真模型的相关参数如表1所示。

表1 仿真参数
图6为储能变流器孤岛运行模式下空载启动波形。由图6可知,电压经过0.01 s达到额定值,交流输出电压THD小于1%。需要说明的是,图中的3条波形对应电压三相电的每一相。

图6 孤岛模式下空载启动波形
图7为储能变流器孤岛模式下由空载切到满载的仿真波形,0.1 s系统由空载切到满载,系统输出电压无明显跌落,交流输出电压THD小于1%。需要说明的是,图中的3条波形对应电压三相电的每一相。

图7 孤岛模式下空载切满载波形
图8为离网模式下交流侧A相电压、电流波形和直流侧A相电压、电流波形。由图8可知,0.1 s负载由空载切到满载,直流侧电流经过0.02 s达到稳定状态且电流纹波较小,交流侧电流稳定后其THD小于1%,系统平稳运行。
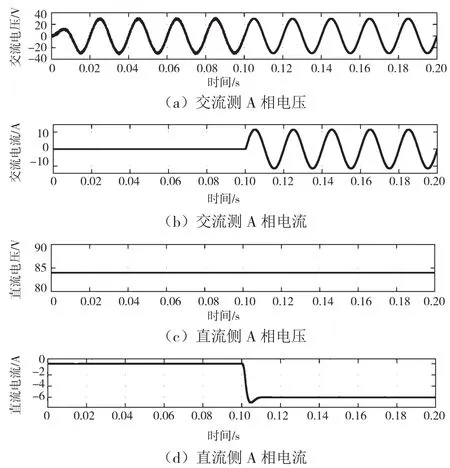
图8 空载切换满载电压、电流波形
图9为系统在空载和满载工况下交流侧输出电压谐波含量分析,可知系统孤岛模式下空载模式下交流侧输出电压THD为0.62%,满载运行模式下THD为0.40%。

图9 A相电压谐波畸变率
通过模拟储能变流器系统并网模式和孤岛模式,对并网模式下系统启动、充放电切换、负载突变以及离网模式下启动带载等工况进行了仿真。仿真结果表明,设计的储能变流器具有响应速度快、平稳运行以及电能质量较高等优点。
4 结 论
本文主要研究储能变流器在孤岛模式下的控制策略,给出了孤岛控制框图,设计了变流器的控制系统,并根据不同的性能指标要求完成了不同工况下系统的电流环、电压外环的设计,最后给出了储能变流器系统在孤岛模式下的MATLAB仿真模型。仿真分析表明,设计的储能变流器具有响应速度快、平稳运行以及电能质量较高等优点。
