生产外包下的服装企业订单分配优化研究
2020-03-27谢雪妍
文/谢雪妍
对于服装企业来说,需要进行产品设计与研发、面料质量检验、产品生产加工、衣服款式确定、产品销售等环节。由于服装行业的特殊性,从产品设计研发到最后送到消费者的手中,大约需要一年的时候,而生产环节前期需要投入大量资金购置机器设备,且后期的场地租金和人工成本也较大,因此企业会将生产环节外包给供应商完成,而将核心竞争力放在产品研发和销售环节。
本文研究的D公司采取的是生产外包模式,把生产面料及成衣的任务交给供应商完成,把自己的优势资源集中在设计研发和终端销售两大模块。生产制造是供应链中重要的一环,因此根据外包供应商的成本、质量和交货能力等指标对其进行生产订单的分配任务显得尤为重要,能够达到降低生产环节成本、提高产品质量和准时交货比率、提高客户满意度的效果。

图1 订单分配影响因素评分
一、相关数据分析
本文选用了D服装公司及其生产外包供应商2018年7月-12月的相关数据,主要讨论泳衣、运动上衣和运动内衣等3款产品及4个供应商之间的订单分配情况。供应商信息汇总表,如表1。D服装公司对各产品的生产需求,如表2。
二、实际订单分配
在实际订单分配任务中,D服装公司会根据工业采购中心计划小组计划员的经验进行分配,主要将供应商分为长期合作供应商和新供应商两类,与D服装公司合作超过两年的供应商为长期合作供应商,不超过两年的为新供应商,其中供应商4(HF)为长期合作供应商,供应商1(DR)、供应商2(DJ)和供应商3(HL)为新供应商。
长期供应商其所分配的订单量大约是新供应商的2倍,同一类型的供应商平均分配订单量。由表2得2018年7月-12月期间3类产品的需求量。表3为各供应商实际订单分配情况。
根据表1的产品报价、固定成本、产品不合格率、交货延迟率等指标数据,结合表3的订单分配情况,可计算出D公司实际订单分配过程中各品类的生产报价总成本、固定总成本、不合格产品数量和延迟交货产品数量。计算公式为:
总成本=生产报价*分配任务量+固定成本
不合格产品数量=产品不合格率*分配任务量
延迟交货产品数量=交货延迟率*分配任务量
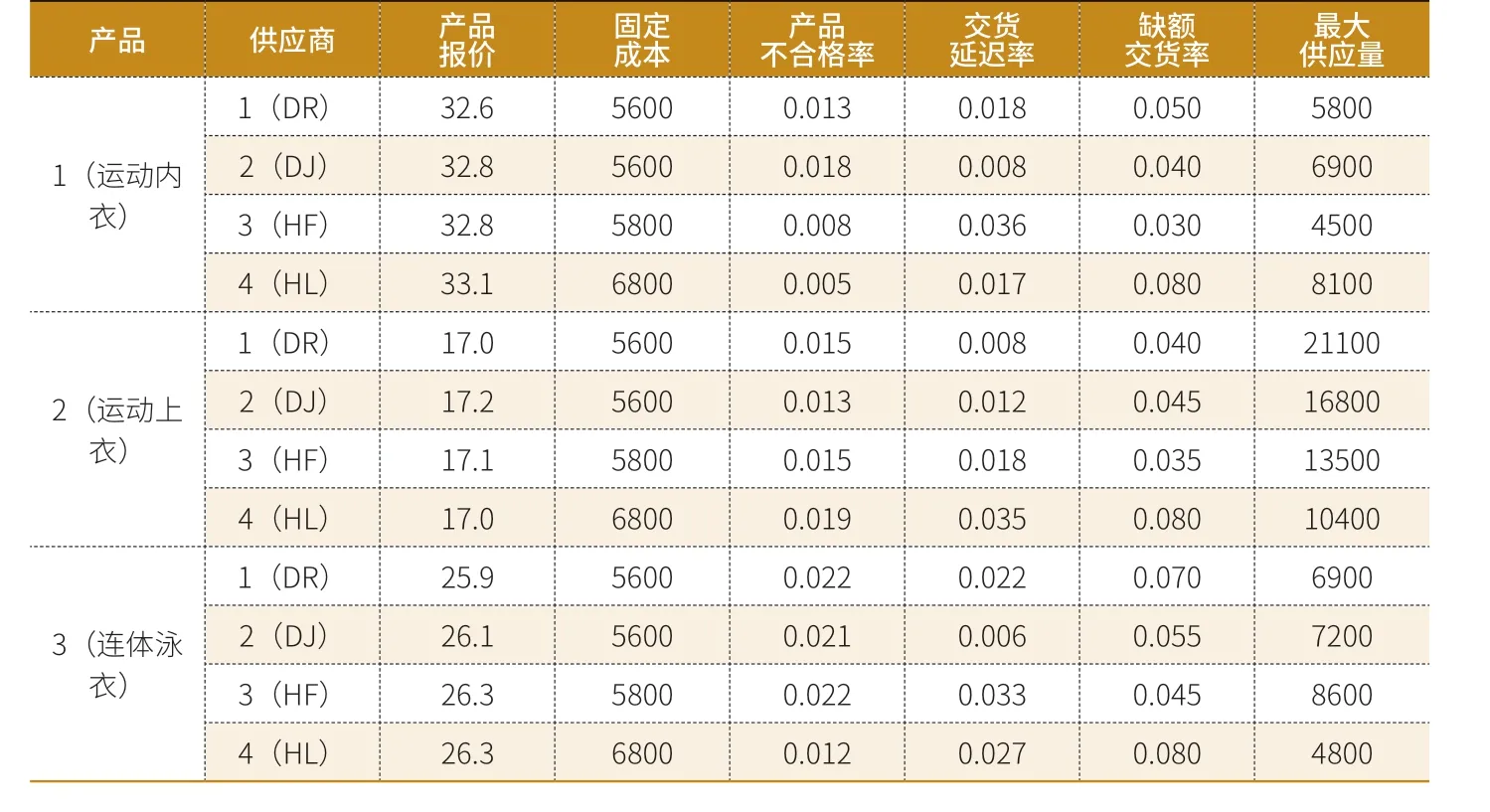
表1 供应商信息汇总表

表2 D服装公司对各产品的生产需求
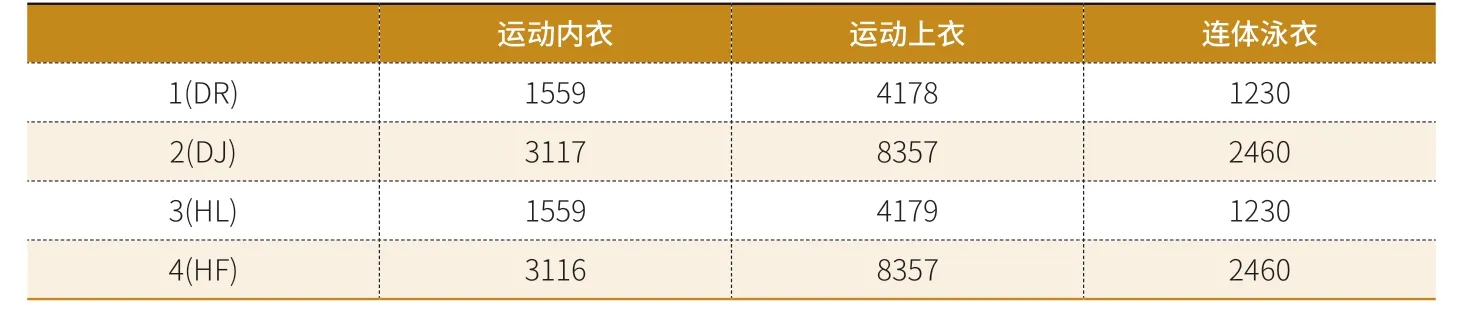
表3 供应商实际订单分配情况
三、模型构建与求解
1.模型影响因素及目标函数权重确定
影响D公司对生产供应商订单选择的因素有很多,通过问卷调查方式选取了7类因素,分别是成本、质量、交货能力、产能、供应均衡、服务、信息化水平,如图1。通过D公司负责对接生产供应商的广州工业采购中心的40名员工对7类因素进行评分,结合因素能否量化和企业内部数据获取的难易程度,选择模型的参数和目标函数。
通过调查问卷的统计结果选择平均得分排名前三的成本、质量和交货能力三个因素作为多目标规划模型的目标函数,产能和供应均衡两个因素作为模型参数在约束条件中体现,服务和信息化水平两个因素因为较难量化、且得分排名靠后,因此不作考虑。
接下来同样利用问卷调查法对质量、成本、交货能力相对重要程度进行评价,整理后的结果为成本相比质量的重要程度为2.55,成本相比交货能力的重要程度为2.4,质量相比交货能力的重要程度为1.75,质量相比成本的重要程度为1/2.55=0.39,交货能力相比成本的重要程度为1/2.4= 0.42,交货能力相比质量的重要程度为1/1.75=0.57。整理形成以下判断矩阵:

Matlab 软件运行结果:w=[0.5490,0.2645,0.1866]T,CR=0.0379<0.1,因此矩阵通过一致性检验。可得成本、质量、交货能力的权重分别为0.5490,0.2645和0.1866,此数据可用在后续多目标规划模型确定各目标的占比。
2.多目标随机规划优化模型的建立
通过构建随机需求下的多目标混合整数规划模型,对选出的4个优质供应商进行3类产品的订单任务分配,其中目标函数为生产报价加上固定成本得到的总成本最小,以不合格产品数量为指标使质量最优,以延迟交货产品数量为指标使交货能力最强为三个目标函数。
以下定义与模型相关的假设条件、符号、决策变量和相关参数。
模型假设:
(1)不同供应商都可以生产每种产品;
(2)产品的需求服从正态分布;
(3)供应商有供应能力限制,即在满交货期条件下的最大供应量;
(4)生产环节以成本、质量、交货能力三个指标为目标,以其他因素作为约束进行订单分配的研究。
符号定义:
i:供应商序号,i=1,2,..n.:
j:产品序号,,j=1,2,..m.;
n:供应商的总数量;
m:产品的种类数;
决策变量:
:企业是否选择供应商i负责产品的生产,若是,yi=1;否则,yi=0
:供应商i是否生产产品j,若是,=1;否则,xij=0
:供应商i生产产品j的任务量
相关参数:
pij:供应商i对产品j的单位生产报价;
fi:供应商i 每个生产周期的总固定成本;
bij:供应商i 供应产品j 的供应能力,即最大供应量;
dij:供应商i 对产品j 的交货延迟率;
qij:从供应商i订购供应产品j的不合格率;
hij:供应商i 对产品j 的缺额交货率。
确定目标函数:
(1)总成本最小:总成本=生产报价成本+固定成本最小化
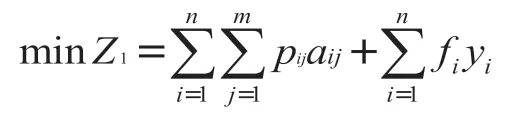
(2)产品质量最优:所有产品不合格数量最小化
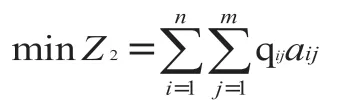
(3)交货能力最强:产品交货延迟数量最小化
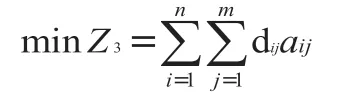
约束条件:
(1)达到一定比例的产品准时交付(准时交货率不小于90%)
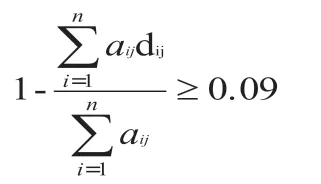
(2)各供应商对每款产品的足额交货率达到一定比例(缺额交货率不超过8%)
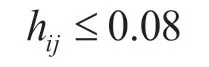
(3)保持订单的均衡分配(单个供应商生产总量小于等于总需求量的75%)
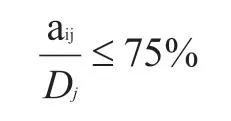
(4)供需平衡(各供应商对于某产品的总生产供应量≥该产品的需求量)
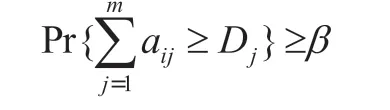
(5)满足供应商产能负荷(最大供应量≥生产供应量)
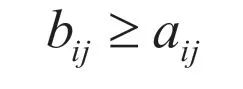
3.模型的求解
本文的订单分配为随机需求下的多目标混合整数规划模型,因此首先要利用机会约束处理随机需求,使得模型变为一般的多目标规划模型。接着,利用最大满意度法确定各目标的隶属度函数,将多目标函数转化为单目标函数进行求解。此模型目标函数中的成本、延迟交货数量和产品不合格数量的单位不相同,因此在求解多目标函数时会出现问题。运用最大满意度法确定隶属度函数能够解决多目标规划模型中各目标函数单位不一致的问题,最终能综合三个目标函数进行多目标函数的求解。
(1)利用机会约束规划处理随机需求
机会约束规划是指当约束条件中含有随机变量时,随机变量出现不满足约束条件的可能,这时需要使约束条件成立的概率不小于某一置信水平。D公司产品的需求量为随机需求,本文把它简化成服从正态分布,利用机会约束可将随机变量等价转换为确定性变量:

其中当落在置信区间的概率为90%时,对应概率函数的反函数为1.28。
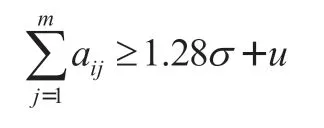
带入软件计算时取等号。
(2)计算各目标函数最大值和最小值
将表1和2数据代入Lingo软件运行,Lingo软件运行结果,如图2。

(3)确定隶属度函数
隶属度函数是模糊综合评价函数中用来综合评价多个影响因素的方法,利用理想向量确定多目标规划函数中各目标的隶属度函数。
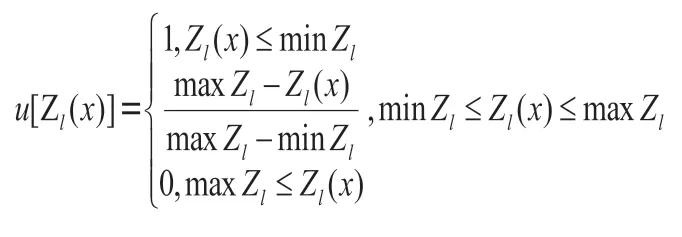
将各目标函数的最大值和最小值代入上述公式可得:

(4)多目标函数转化为单目标函数求解
确定了各目标的隶属度函数后可利用最大满意度法将将多目标函数转化为单目标函数。定义为最大满意度,则最大满意度满足:
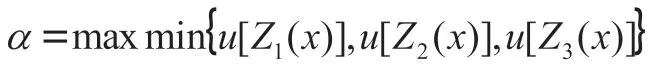
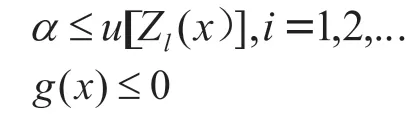
(5)目标函数加权处理
利用4.1得出的各目标重要程度权重对最大满意度进行加权可得:
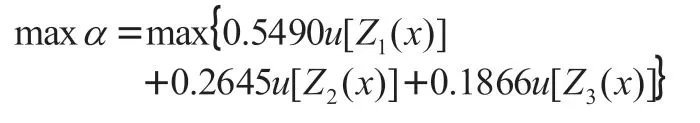
4.模型结果分析
利用多目标混合整数随机规划模型对D公司订单分配任务进行求解,相比于原来仅凭经验分配订单,使得订单分配有多个方面的优化效果,订单分配模型结果,如表4。
(1)优化生产环节的总成本、产品质量和产品交货能力
优化前后的成本、质量、交货能力对比,如表5。其中,总成本降低了2.3%,产品不合格数量和交货延迟数量分别降低了48.6%和51.4%,证明本文所运用的供应商选择方法和订单分配模型对D公司生产环节具有优化效果。
(2)考虑供应商的综合能力
由表4可得,在产品类别3(连体泳衣)中,供应商DJ比供应商DR的成本要高,但因为供应商DJ的质量和交货能力方面比供应商DR更有优势,因此分配给DJ的量更多。这说明了在多目标规划模型所选定的是成本、质量和交货能力三个目标而非单一目标,并按各权重得到最终结果,这样能够使D公司在多个方面对供应商的综合能力做出评价,从而更有依据地完成订单分配的任务。而在D公司实际订单分配流程中,没有以目标为导向,简单地进行平均分配,没有依据性。
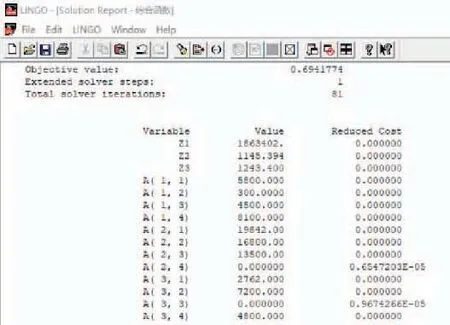
图2 Lingo软件运行结果
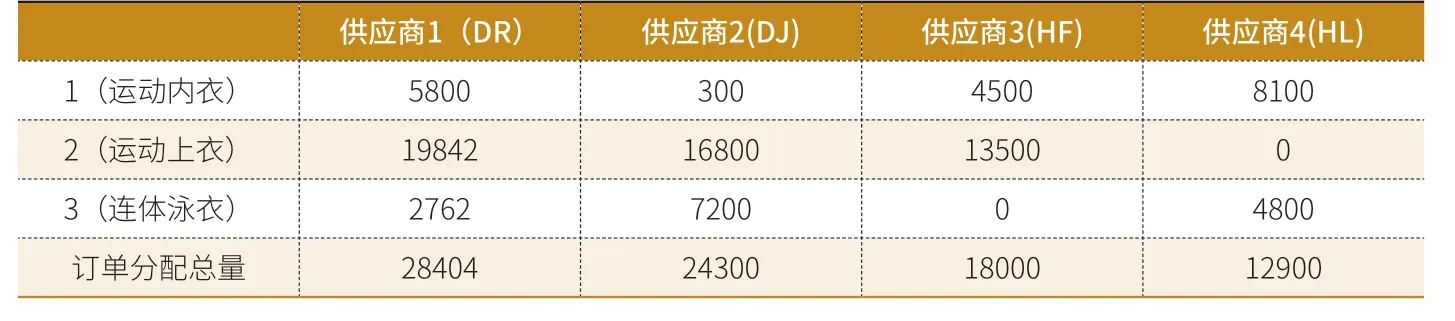
表4 订单分配模型结果
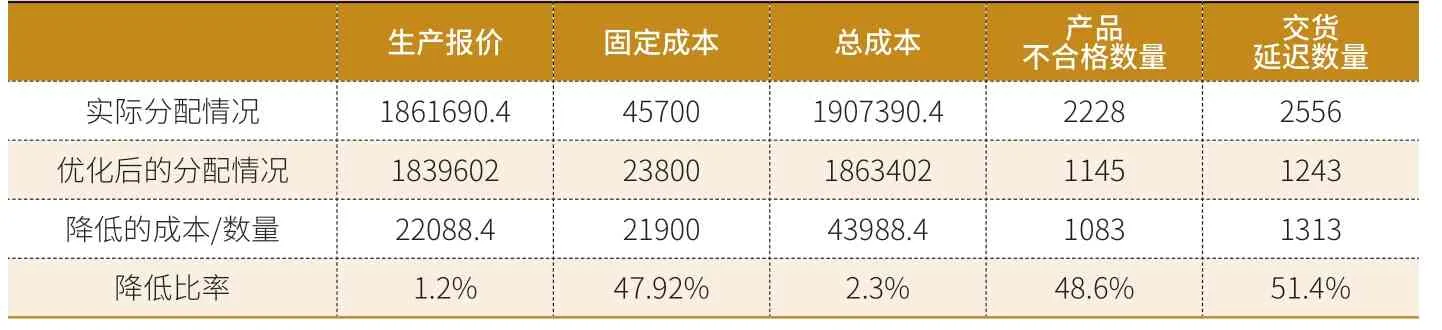
表5 优化前后的成本、质量、交货能力对比
(3)考虑各目标的重要程度
分析表1和表4数据可发现,在产品类别1(运动内衣)中,供应商2(DJ)的交货延迟率为0.8%,相比另外三个供应商来说交货能力最有优势,但因为4.1小节中所算出交货能力的权重较小,供应商2(DJ)在产品1中的综合能力排名仍然靠后,因此所分配到的订单量较少。因此,不同目标的权重对模型结果十分重要,在确定权重时要全方位考虑,如本文中的权重采用D公司工业采购中心的40名内部员工的评分数据,他们与生产供应商的接触最密切,评价出来的分数具有说服力。
在实际订单分配流程中,D公司仅凭计划员和供应链经理等人的经验和主观意见进行订单分配任务。而此优化模型综合考虑了影响订单分配的多方面因素,且模型数据容易获取,能够对D公司的订单分配任务进行改进和优化,且在日后能定期统计更新供应商的数据,使模型结果更准确。
四、总结
在订单分配优化模型中,舍弃了D服装公司参考以往订单分配方案和依赖计划小组计划员进行订单分配的主观方法,改为采用随机需求下的多目标规划模型,设置了成本最小、质量最优和交货能力最强三个目标,供应商最大供应量、D公司产品需求量、订单均衡等因素为约束条件,根据目标函数和约束条件分配生产任务,接着运用机会约束和最大满意度法求解多目标随机规划模型,最后得到订单分配结果。
通过实证分析结果表明,本文订单分配优化策略有效地降低成本、提高质量和准时交货率。
