基于高斯过程的TGDI发动机充气模型试验研究

徐宁宁 张文韬 郑海亮 王艳龙 陈立 郝伟 闫涛

（中国第一汽车股份有限公司 研发总院，长春 130013）

主题词： 充气模型 高斯过程 模型精度 DoE 模型试验验证

1 前言

降低排放、改善油耗一直是各大汽车厂商追求的目标，可变气门正时、进气翻板、可变容积腔等技术被广泛应用以改善汽油发动机进气和燃烧特性。随着可变机构数量的增加，需要标定的MAP呈指数级增加，发动机试验台试验任务量急剧增加。以神经网络（BP）为代表的人工神经网络已被证明是一种适用于变量化的标准多输入黑箱模型[1-2]，然而神经网络易出现因过学习而导致的泛化能力差、网络结构难以确定的问题；支持向量机也有其局限性，例如，需采取适当惩罚函数防止过度拟合、难以推广到多类问题等。高斯过程模型通过结构风险最小化原则描述过度拟合与泛化能力之间的关系，可有效地提高对小样本问题的预测性能[3]。

本文通过对发动机进气过程进行物理特性分析，阐述充气模型的基本原理，通过试验对训练数据进行采集，并采用高斯过程模型评估相对进气量，采用稳态和慢动态数据进行验证，结果表明，精度良好，可以作为黑盒模型用于ECU控制算法开发以及虚拟开发。此外，本文研究了减少训练数据点和减少输入参数对高斯模型精度的影响。

2 充气模型原理

准确评估发动机充气模型的重要前提是理清影响充气的主要因素，本文基于物理分析的方法，找到影响充气的主要因素并建立模型。充气模型[4]来源于进气门开启到进气门关闭期间进气过程的物理分析。根据理想气体方程PV=mRT，缸内气体质量在进气门关闭时缸内状态为：

在标准大气压，0℃状态下气体质量为：

相对气体质量：

缸内气体成分主要有新鲜空气和残余废气，残余废气又分为滞留废气与回流废气，则缸内新鲜气体相对量：

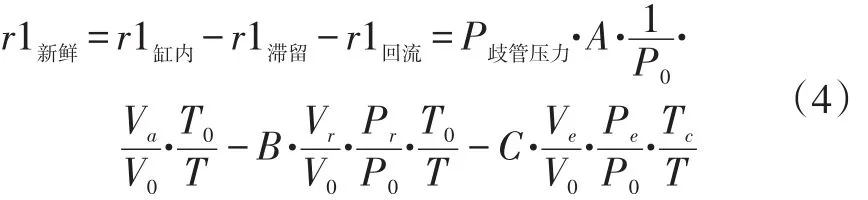
式中：A为歧管压力到缸内气体压力的修正量；B为对滞留废气体积的修正量；Vr为排气关闭时缸内气体体积；C为对回流废气体积的修正量；Ve为回流气体体积。

充气模型逻辑如图1所示。

图1 充气模型逻辑

3 充气模型试验研究

3.1 试验对象

本次试验采用一款2.0 L增压直喷四缸发动机，发动机的参数如表1所示。

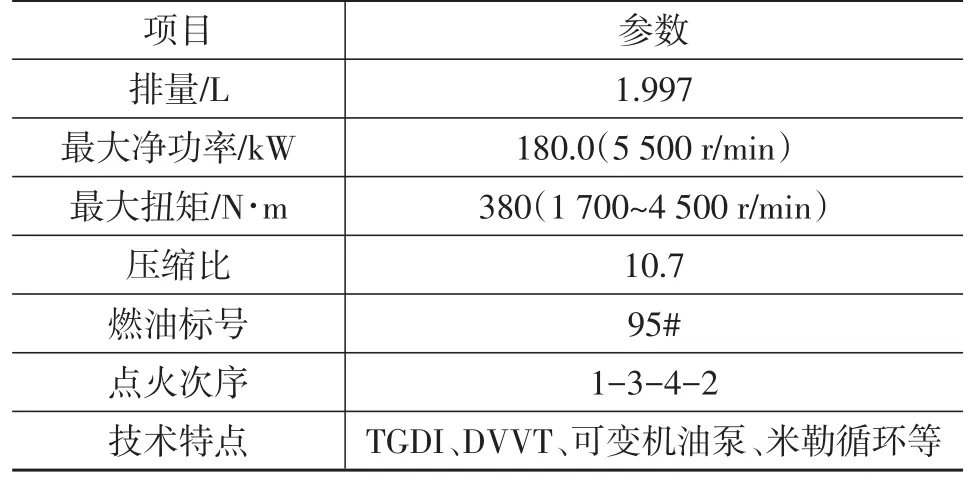
表1 发动机参数

试验中使用的设备及系统构成如图2所示。

3.2 数据采集

输入、输出参数对建模有重要影响，发动机充气取决于进气歧管条件，即Pim和Tim以及由气缸体施加的边界条件。发动机转速具有足够的代表性描述气缸内的充气现象，进排气可变气门正时（DVVT）对气流运动也有着重要影响。本文采集不同转速、不同DVVT组合下的歧管压力。试验采集的变量如表2所示。对于测得的数据集，用于高斯过程训练，同时另测一组万有特性及慢动态数据，用于验证模型。

3.3 数据处理

3.3.1 数据处理方法

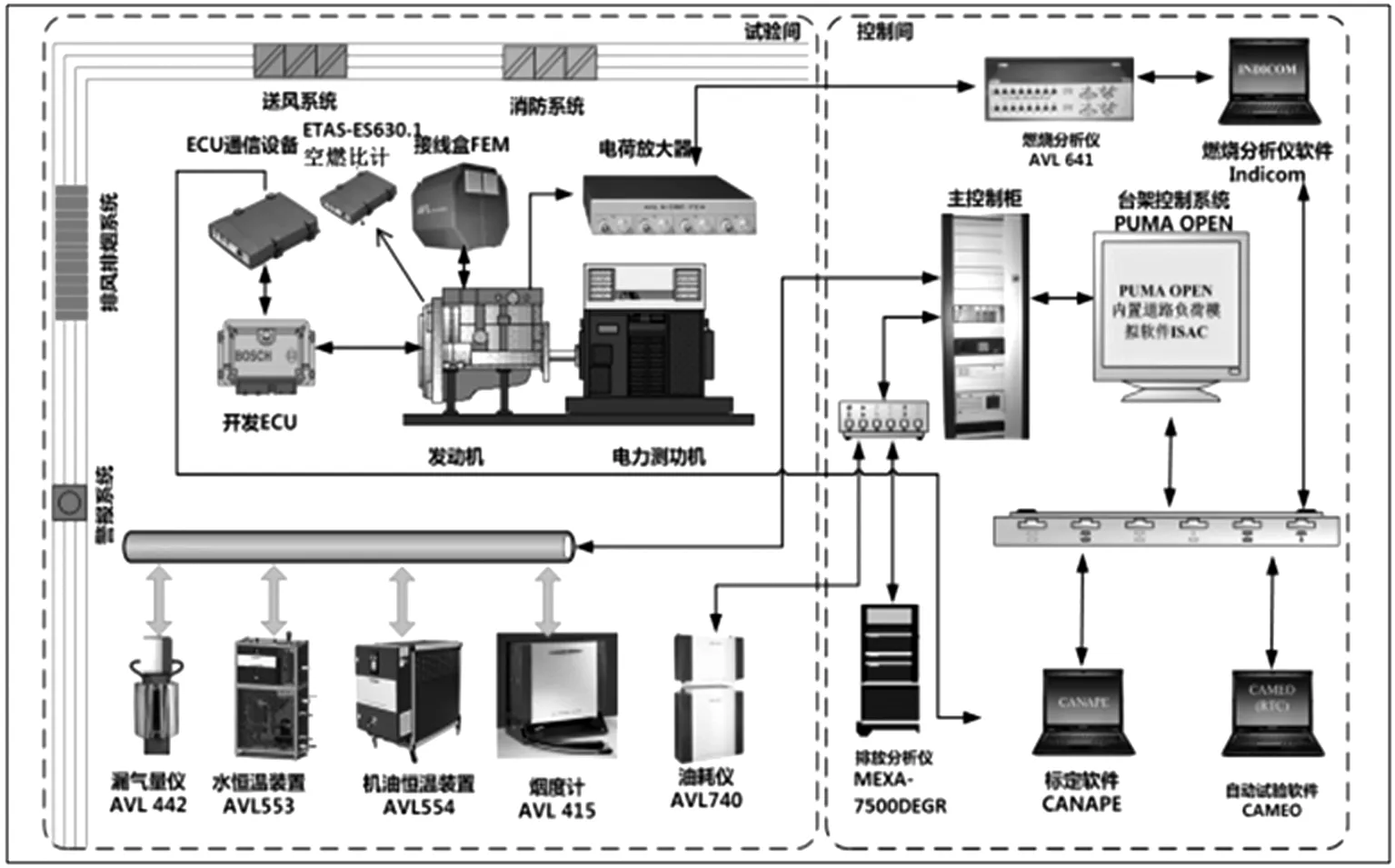
图2 试验装置及系统（横排版）

高斯过程又称正态随机过程，其基本思想是赋予假设空间一个高斯过程先验，噪声必须满足高斯分布。任意有限变量集合都有着联合高斯分布的特性，其全部统计特征完全由它的均值和协方差函数来确定[5]。但是许多实际情况并不满足这个假设，因此对其进行统计分析时需对数据进行转换，使得变换后的数据符合正态分布。本文采用平方指数协方差函数，对数据进行Box-Cox变换，并采用LOO（Leave One Out）交叉验证方法防止模型过于复杂而引起的过度拟合。对于不同的输入变量，定义不同的长度尺度，理论的联合高斯分布为下式。

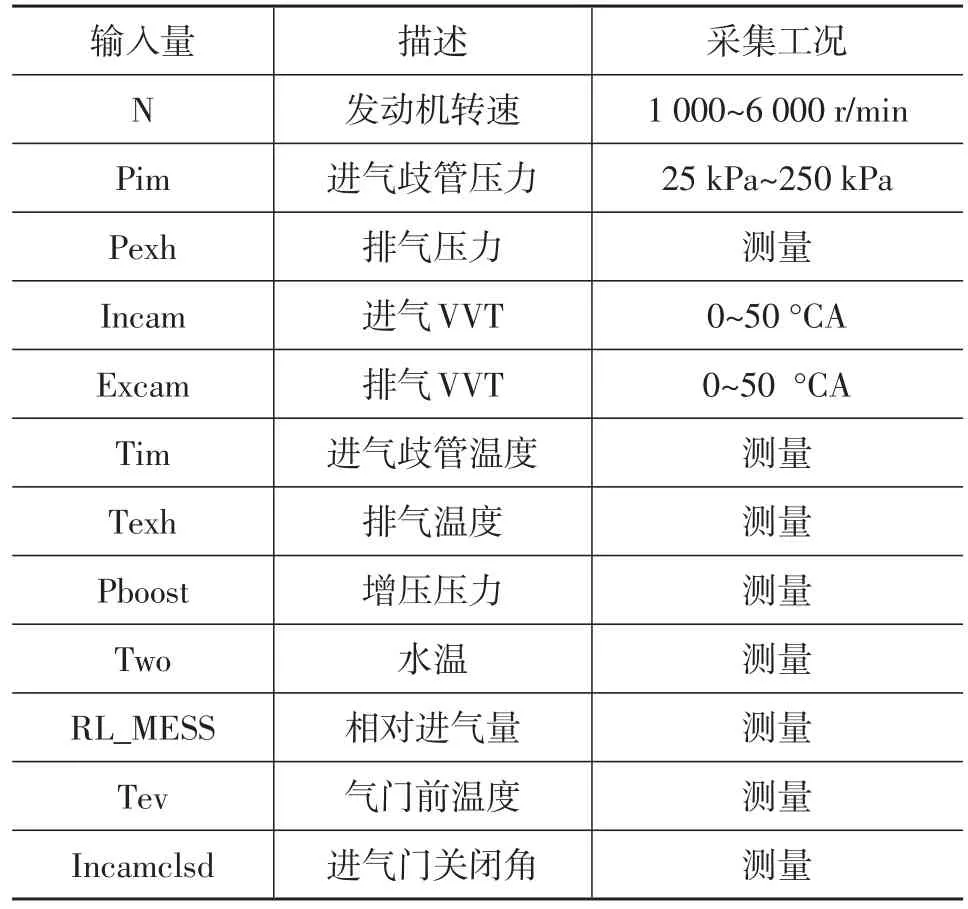
表2 试验采集工况

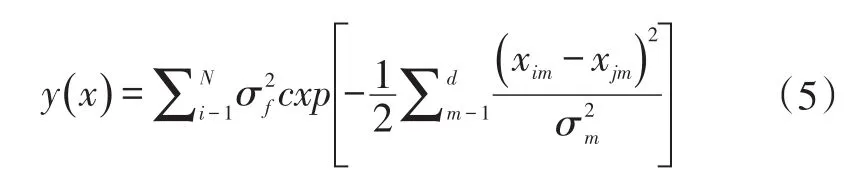
式中：σm代表d（m=1,2,……d）维空间每个变量的长度尺度；σf是核函数的信号方差，用来控制局部相关性的程度；θm=logσm；θd+1=logσf。

3.3.2 高斯过程训练

本研究采用的稳态工作点集含6 273个点，该点集由所采集的输入量及相应的变化量组成，代表高维模型输入的全因子映射。在训练中使用全部点集，进行交叉验证，通过标定数据集上的残差最小化平方和实现该模型的识别，建模训练方式如图3所示，训练结果如图4、表3和图5所示。

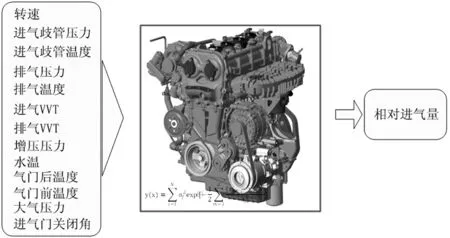
图3 建模训练方式

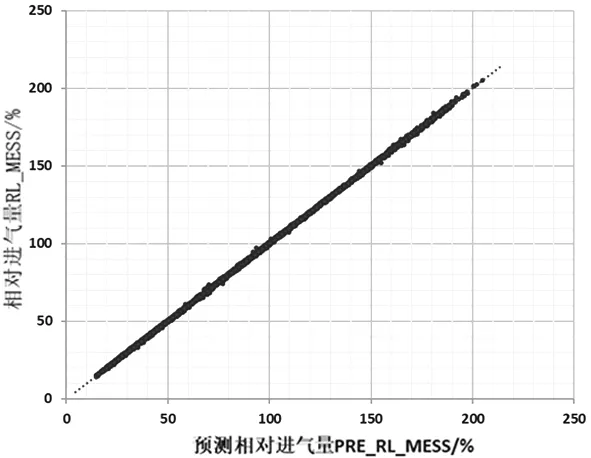
图4 实际相对进气量vs模型预测

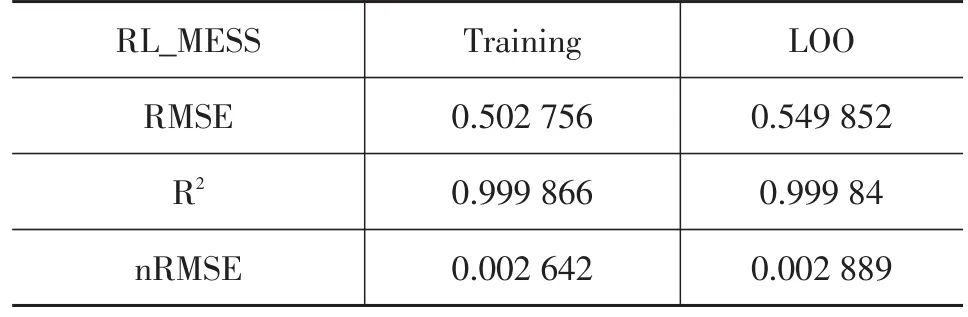
表3 统计结果

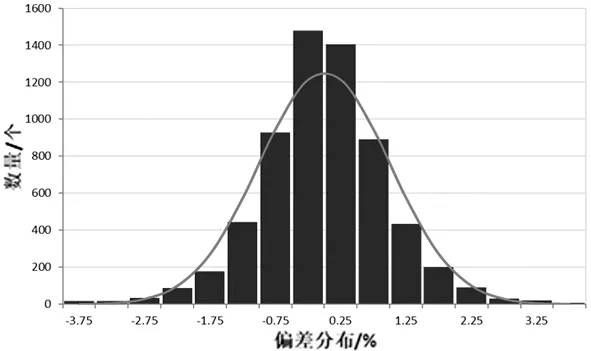
图5 偏差分布

3.4 模型验证

3.4.1 稳态点集

当高斯过程参数化完成，需要对模型进行评估，检查在训练数据集上获得的性能是否代表模型的实际行为，防止过度参数化。验证数据集必须与要使用的模型紧密相联且相互独立，采集发动机万有特性中共318个点用来验证，以获得更好的验证评估效果。可接受模型的标准是95%的点误差在±5%以内，否则，模型将被拒绝，稳态验证相对进气量偏差如图6所示。

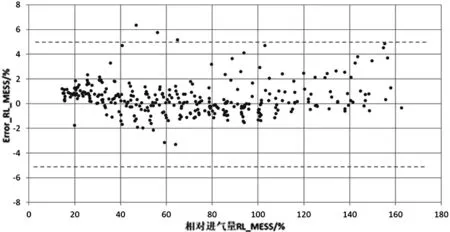
图6 稳态验证相对进气量偏差

3.4.2 慢动态点集

采集发动机的慢动态数据用来验证，以获得更好的验证评估效果，慢动态工况如图7所示。慢动态数据验证整体的趋势与稳态点相似，整体结果较好，慢动态工况验证相对进气量偏差如图8所示。

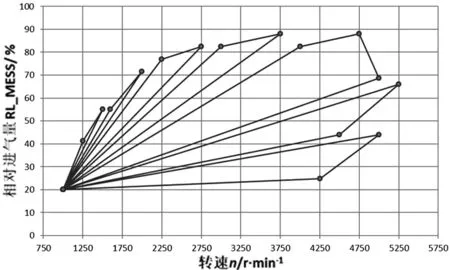
图7 慢动态工况

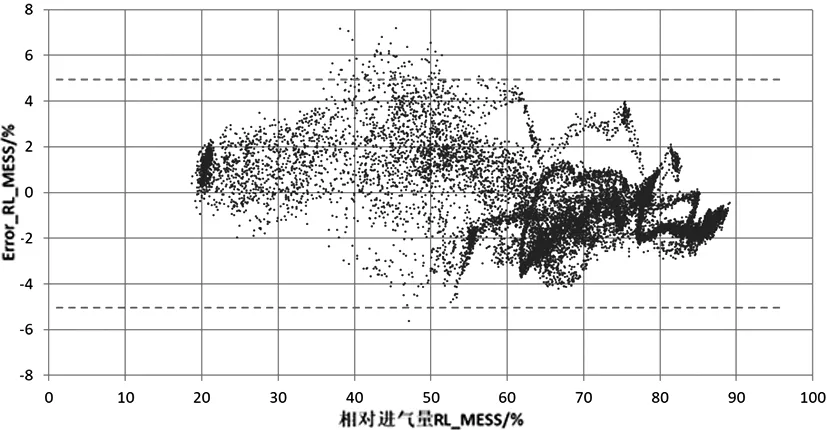
图8 慢动态工况验证相对进气量偏差

3.5 高斯模型精度影响

3.5.1 减少数据点对模型精度影响

获得广泛的数据集是高斯过程训练和验证的关键，考虑到范围越宽，使用高斯模型获得的不期望行为的风险就越小。然而，获得数据集的台架试验工作量非常繁重，在该情况下，应该考虑获得期望性能所需的最少点数，所使用操作点的数量和点的空间分布是高斯模型的一个重要问题。空间填充方法和拉丁超立方体抽样方法是近年来常用的DoE方法[6]。本文并未采取直接减少训练数据点的方法，而是在所有数据中采用空间填充的方式从模型中随机抽取数据点，分别抽取1 500个和3 000个，以分析获得最优高斯模型的精度所需要的最少的点。图9、图10分别为采用1 500个和3 000个点建模的稳态验证，可以看出，采用DoE减少数据点，模型精度会有一定的发散，但考虑到抽取数据点不是实测数据，而是通过已经训练的模型获得，本身就存在一定的误差，故采用的数据点增加模型精度有较大改善。

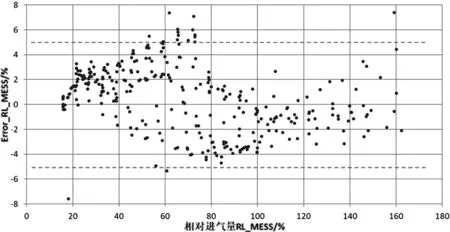
图9 采用1 500个点建模的稳态验证

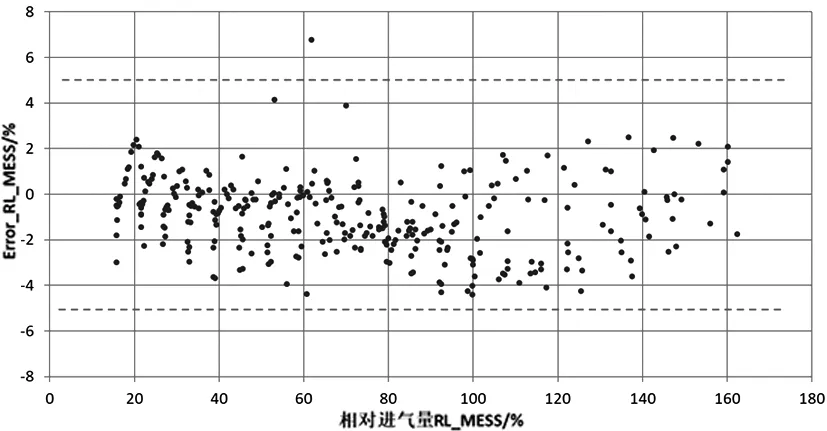
图10 采用3 000个点建模的稳态验证

3.5.2 减少输入参数对模型精度影响

在选择高斯模型输入进行在线实时应用时，物理规律和计算量需求都必须要考虑到，后者直接与高斯模型的输入数相关。本研究尝试减少输入变量个数来检测模型精度的变化。图11为输入与输出的相关性，可以看出输入与输出的相关性大小不一，综合考虑物理规律与相关性后，去除气门前温度、水温、进气门关闭角等输入量。图12、图13为减少变量重新训练并采用稳态点集与慢动态点集验证的结果，模型精度并未变差。

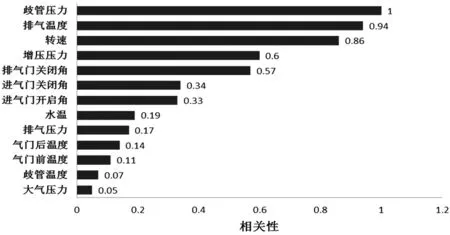
图11 输入输出的相关性

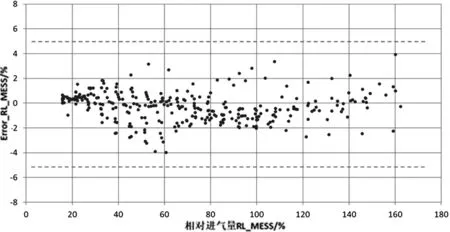
图12 稳态点集验证结果

图13 慢动态点集验证结果

4 总结

本文采用高斯过程，结合物理规律分析，对一台增压直喷、DVVT汽油机进行充气模型的研究，得出以下结论。

（1）可变结构的增加将导致控制策略的复杂性与标定工作量的急剧增加，而高斯过程模型处理各种输入的增加有很大优越性。

（2）通过稳态点与慢动态点对高斯过程模型进行验证，结果良好，证明模型具有较强的泛化能力。

（3）选取合适的DoE，可以大大减少数据点的数量，降低试验工作量，而准确性没有重大损失。

（4）输入参数的选取对高斯过程模型有较大影响，可以根据输入、输出相关性及物理规律，适当减少输入参数以降低空间维度，减少计算量，同时能保证模型精度无重大损失。

该经验模型可以作为黑盒与物理模型相结合，用作虚拟标定或控制策略的开发，甚至可以转成代码作为ECU中的一部分。

本文只研究采用高斯过程对进气进行建模，对于燃烧过程、扭矩模型也可以采用类似的研究方法。