财务报表审计重大错报风险评估研究——基于熵权TOPSIS和灰色关联度法

重大错报风险的评价方法主要为模糊评价法和层次分析法，前者实现了审计风险的量化评价，但专家打分的环节存在一定主观性；后者可以用较少的指标数据完成审计风险评价，但难以计算大量的统计指标数据，且权重界限确定模糊。为了改进评价方法的科学合理性，本文提出熵权TOPSIS和灰色关联度相结合的方法，对审计重大错报风险进行评估。熵权法中的“熵”，主要用来度量信息的不确定性。在重大错报风险评价中，用各指标的信息熵来反映其变异程度。信息熵越小，表明其与标准值的差异较大，提供的信息量多，权重越大，反之权重越小。TOPSIS法通过计算各样本与正负理想解的几何直线逼近距离择优，但无法反映其变化形态。灰色关联度法通过衡量各指标发展态势的相近程度，来评价其与理想解的关联程度。将TOPSIS法与灰色关联度法结合可以同时考虑与理想解的接近程度和关联程度，使评价更客观、合理。

一、重大错报风险评估模型构建

（一）构建评价指标体系

重大错报风险往往伴随着财务报告异常特征指标的波动，故分别从偿债、营运、盈利、发展四个方向选取指标，并在每个一级指标下选取若干二级指标，对重大错报风险进行客观合理评价，如表1所示。

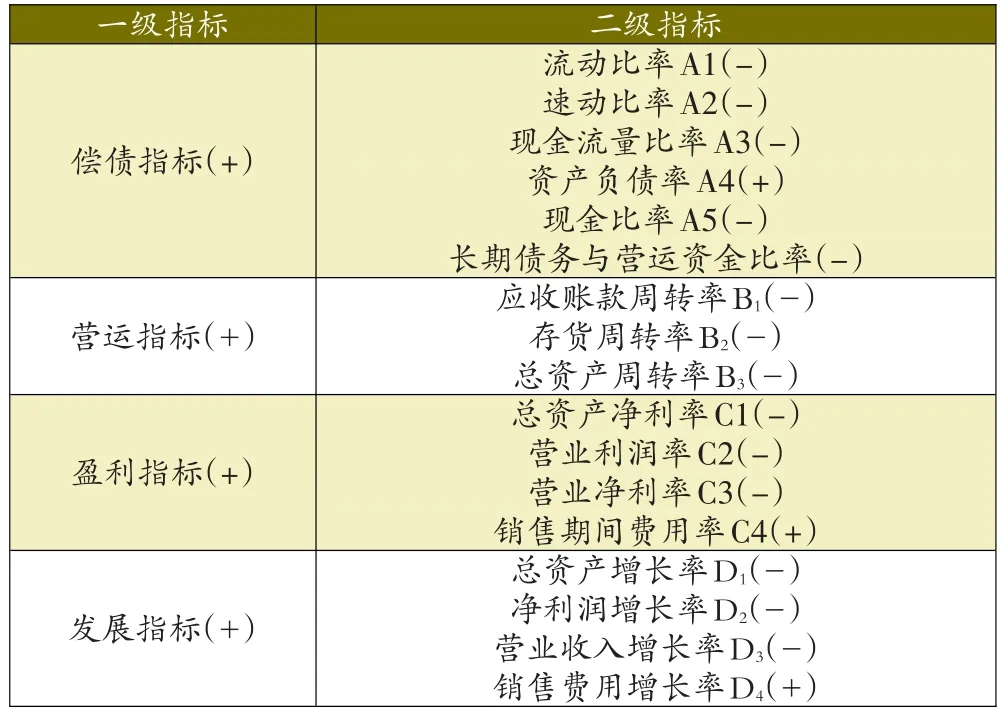
表1 重大错报风险评价指标体系

资产负债率越高，表示该企业为保持运营所背负的负债越高，企业资不抵债，存在重大错报风险的可能性较大；销售期间费用率、销售费用增长率越高，表明企业营销花费较高，可能存在资金行贿行为，重大错报风险较大。故以上三项为正向指标，即该项指标值越大，发生重大错报风险的可能性越大。其他指标为负向指标。

（二）构建综合评价模型

针对上市公司重大错报风险评价指标体系，建立基于熵权TOPSIS法与灰色关联度法结合的综合评价模型。首先利用熵权法确定各个重大错报风险评价指标的权重，用TOPSIS法计算各样本的正负理想解，以各指标对理想解的相对贴近度为基准对样本进行初步评估。再利用灰色关联度法计算各样本与正负理想解的关联度，将二者结合，计算出更加精确的理想解贴近度，以此实现最终的决策评估。

1.构建指标矩阵

假设对X={X1，X2，…，Xn}个公司的重大错报风险进行评价，共包含Y={Y1，Y2，…，Ym}个评价指标。构成指标矩阵A=(aij)n×m，其中xij为第i个公司的第j个指标，i=1，2，…，n；j=1，2，…，m。

2.指标矩阵规范化

对各指标数据进行规范化处理，得到无量纲决策矩阵B=(bij)n×m。若数值越大，重大错报风险越大，则规范化：

若数值越小，重大错报风险越大，则规范化：

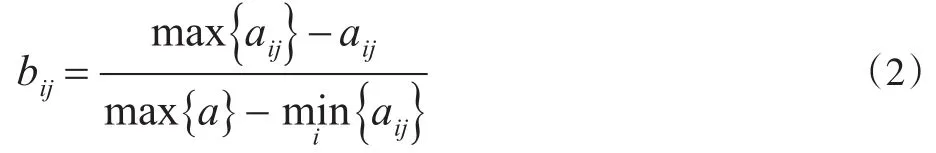
3.归一化处理

将矩阵B归一化，得到矩阵C=(cij)m×n，其中：

4.熵权法确定各指标权重

定义第j项指标的熵值为：

则第j项指标的熵权为：

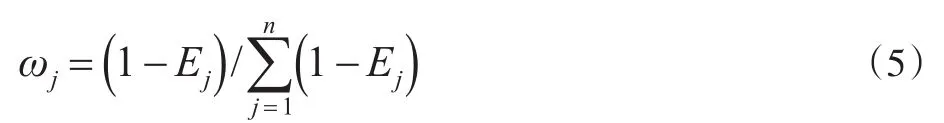
5.指标矩阵加权标准化

将规范化后的指标矩阵与对应的权重相乘，得出加权标准化决策矩阵：

6.确定正负理想解

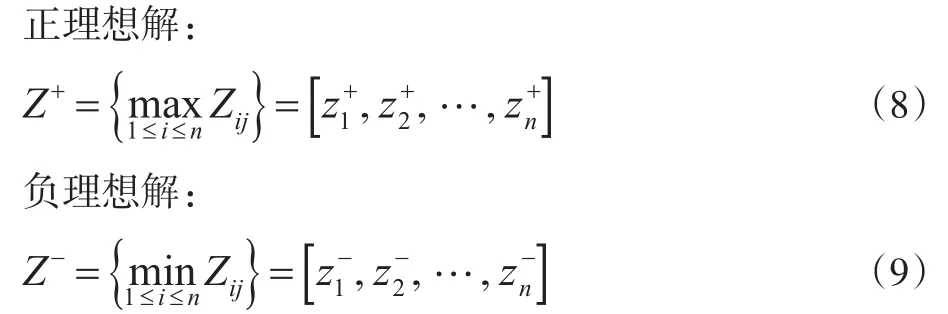
7.计算欧式距离

计算各样本到正负理想解的欧式距离di+和di-：

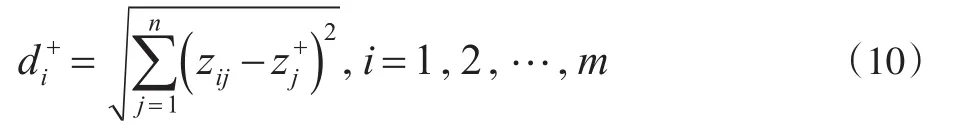
8.计算各样本与正、负理想解的灰色关联系数

根据式（6）的加权标准化决策矩阵，确定第i个样本对正理想解的第j个指标的灰色关联系数：

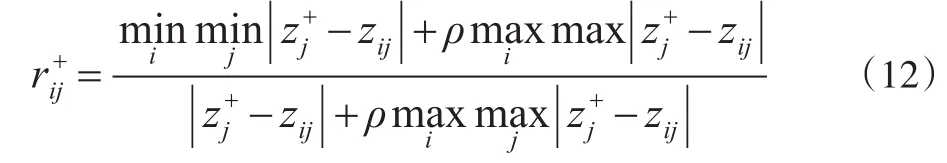
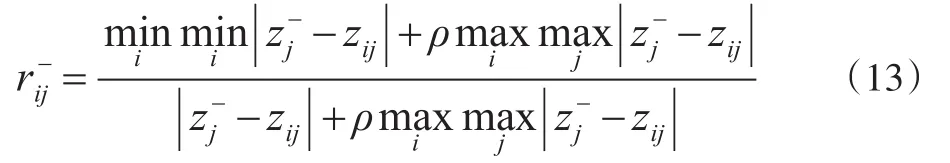
9.确定样本与正负理想解的灰色关联度

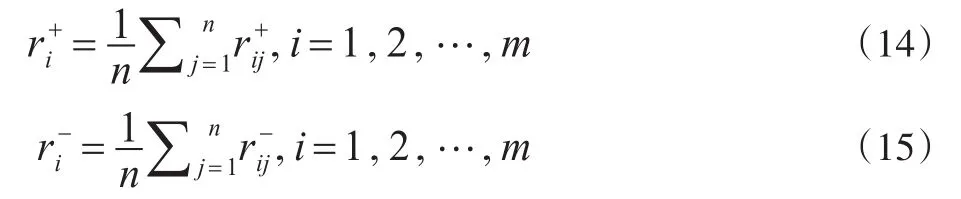
10.无量纲处理欧式距离和灰色关联度

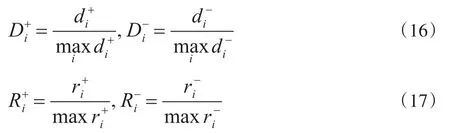
11.融合无量纲化后的灰色关联度和欧式距离

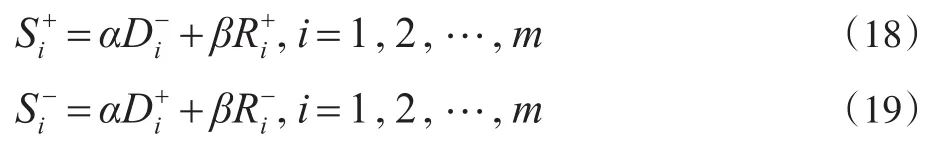
式中：αβ满足α+β=1，αβ∈[0，1]，使用者可根据自己的偏好确定它们的值。Si+综合反映了样本与正理想解的贴近程度，其值越大重大错报风险越大;Si-则反映了样本与正理想解的远离程度，其值越大重大错报风险越小。

12.计算相对贴近度

相对贴近度反映了各样本与正理想解的贴近程度：

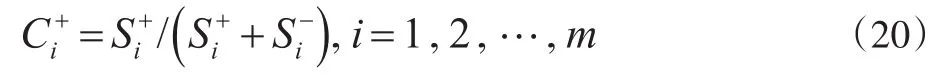
二、实证分析

2018年12月，康美药业被证监会立案调查，其受托事务所广东正中珠江会计师事务所成为社会焦点，故本文选取由正中珠江会计师事务所审计的5家医药制造业公司作为样本，分别为太安堂、汤臣倍健、博济医药、康美药业、维力医疗，剔除了检查风险及行业因素的影响，对财务报表审计重大错报风险进行评价。通过国泰安数据库及上市公司财务报表，查询汇总各指标数据如表2～5所示。

表2 偿债指标

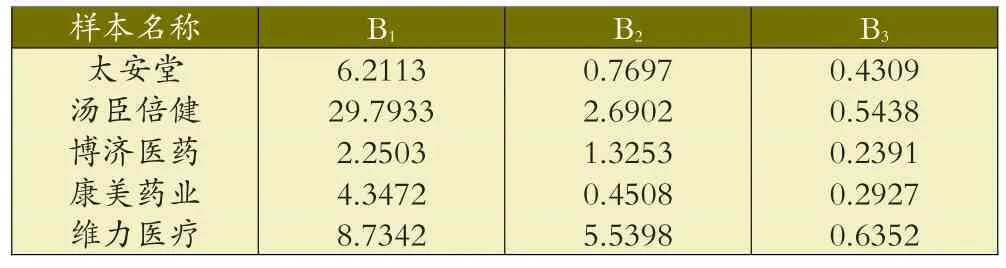
表3 经营指标

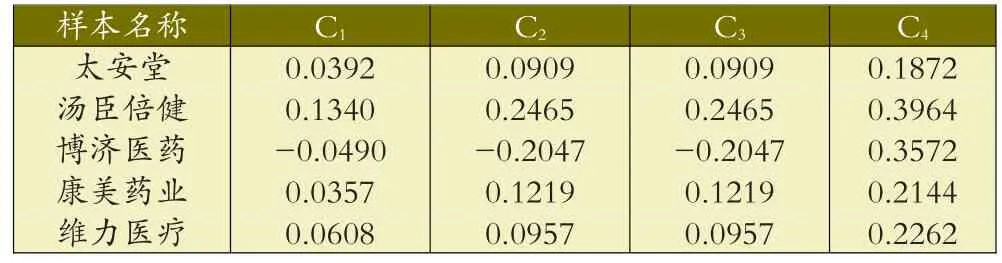
表4 盈利指标

由公式（1）～（6）计算各重大错报风险评价指标权重，得结果为ω=（0.2348，0.1382，0.2700，0.3545）。

由公式（7）～（9）将指标矩阵规范化，并计算正负理想解，得：

Z+=（0.2348，0.1311，0.2540，0.2610）

Z-=（0.0140，0.0296，0.0705，0.0035）

由公式（10）、（11）计算各样本与正负理想解的欧式距离，得：

由公式（12）～（15）计算各样本与正负理想解的灰色关联度，得：

根据公式（16）、（17）将欧氏距离和灰色关联度进行无量纲化处理，得：

令α=β=0.5，由公式（18）～（20），计算各样本与正理想解相对贴近度，得Ci+=（0.3622，0.3416，0.6870，0.6115，0.2785）。

由于相对贴近度C越大，样本的重大错报风险越大，根据计算结果可知，重大错报风险排序为：博济医药＞康美药业＞太安堂＞汤臣倍健＞维力医疗。博济医药，早在2016年就被报出财务数据造假的舞弊事件，康美药业也已于2018年被证监会立案调查，二者四项指标值都较高，重大错报风险大。汤臣倍健、维力医疗经查未存在被出具保留意见的审计报告，说明公司状况良好，其经营指标和盈利指标较好，重大错报风险小。

三、结语

本文建立了基于熵权TOPSIS和灰色关联度分析法的重大错报风险评价模型，克服了传统的单一TOPSIS法或者灰色关联度分析法在评价过程中一部分评价信息丢失的缺点，提高了评价结果的科学性。此外，运用熵权法确定各个评价指标的权重，能够充分利用所得到的信息，使得确定的评价指标权重更加客观。通过对2017年正中珠江会计师事务所审计的5家医药行业上市公司重大错报风险进行评估，证明该评价模型有效可行。基于TOPSIS-灰色关联度分析法的评价模型为重大错报风险的评价提供了一种新思路，根据比较相对贴近度的计算结果，可以根据从大到小的原则对国有上市公司的重大错报风险进行排序，评价结果清晰明了，为财务报表审计重大错报风险评估提供了技术支持。