基于T-JIT理论背景下的双渠道供应链协同风险优化研究

郝 丽，郝新军，胡大伟，李 晨

(1.西安财经大学 管理学院，陕西 西安 710100；2.长安大学 汽车学院，陕西 西安 710064；3.山东交通学院 汽车工程学院，山东 济南 250357)

0 引言

随着“大数据、云计算、区块链、人工智能、互联网+”等先进信息科技的发展，物流行业的发展空前高涨，第三产业的比重也在持续增加，而物流行业也在朝着数字物流方向发展。Kenneth首次提出Total Just In Time(T-JIT)的理论，其概念突显了当代数字化供应链的新领域，T-JIT理论的创新之处在于把传统的3个JIT即JIT生产、JIT采购、JIT销售变成4个JIT的概念，即新增加了JIT信息，主要集成考虑其在上述4个JIT理论融合的过程中对整个供应链管理策略的影响[1]，其理论结构如图1所示。目前双渠道供应链的网络化、信息化是物流4.0时代的新趋势，即传统企业的营销模式与网络直销渠道如何平衡线上、线下协同，同时对双渠道供应链协同机制的研究既是机遇又是挑战。挑战在于双渠道供应链无论哪个环节的信息共享率和风险弹性受到波动，直接造成整个供应链物流、信息流、资金流、人流的动态链接中断的可能，无法实现价值链的增值。风险管理与协同管理的柔和形成了供应链管理的核心，也是其价值增值过程的源泉。考虑T-JIT理论背景下双渠道供应链如何通过有效的合作来降低风险，解决双渠道供应链协同管理的风险评价优化问题已经成为学术界研究的热点，该研究可进一步完善供应链协同风险管理理论体系。为了保证网络化、信息化的双渠道供应链协调发展，首先需对双渠道供应链协同的风险管理进行研究，国内外学者已经做了有意义的探讨。

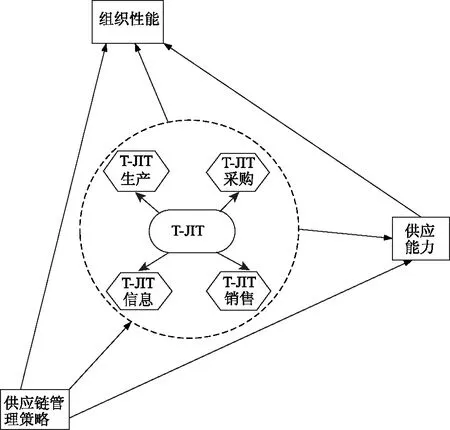
图1 T-JIT理论模型

20世纪90年代末，B2B、B2C等电子商务的兴起促使国外专家对双渠道供应链的协同风险的研究比较重视，主要表现为Y.Li等提出一个风险预警和实践控制系统的框架结构来研究食品供应链网络中的应用问题[2]。Gang Li等创新性地从一个整体机构和协同视角研究集成的供应链风险管理[3]。Frank Wiengarten等研究了供应链整体集成系统，即考虑风险、风险管理实践来集成整个供应链并进行有效管理[4]。MihalisGiannakis等从绿色供应链独特的视角下研究供应链的可持续发展，研究方法主要是供应链风险管理方法[5]。Tsan-Ming Choi等从中断风险管理、运营中风险控制、灾难和突发事件的管理、物流服务风险分析这几个方面对整个供应链系统风险进行研究，体现整体协同的管理思想[6]。AndraBadea基于供应链管理实践，应用层次分析法研究影响供应链的两个协同概念(水平和垂直)对整个供应链的风险的影响[7]。Fang Zhang等研究了在考虑服务价值的双渠道供应链下灵活的价格策略和协调问题[8]。

图2 双渠道供应链协同风险影响因素

国内主要侧重于单独对供应链协同管理、风险管理进行理论和方法的创新研究，但是考虑风险与协同融合概念下整体供应链的协同风险管理研究还比较少。主要代表是李真通过统计方法分析对影响供应链风险预警指标体系进行评估[9]。李艳萍侧重于可持续供应链的角度对广西传统制造业供应链风险管理与对策进行研究[10]。程国平研究了生产-库存系统、库存-分销系统和生产-分销系统的协同，提出了一种合理划分协同利润的方法[11]。方忠民对契约合作与信息共享的供应链协同进行研究[12]。郑庆华研究了林业绿色供应链物流的一体化管理的物流特点[13]。董珊珊等对绿色供应链协同问题进行综述研究，提高整条供应链的效率[14]。温磊主要侧重于供应链协同管理方法上的创新，主要是运筹学和模糊数学理论的结合下进行方法创新[15]。许民利等探讨了在不同风险偏好下双渠道供应链定价决策问题[16]。徐琪等研究了双渠道供应链库存协调合作策略[17]。

综上所述，学者们侧重于对供应链风险评估和控制机制进行研究，还没有学者以T-JIT为背景对双渠道供应链线上、线下如何协同管理进行风险优化研究，着重考虑JIT信息对双渠道供应链各节点企业内部的风险优化，达到整体利益最大化的目的。本研究借助数理统计理论、运筹学和博弈理论对双渠道供应链风险指标进行识别，采用因子分析法(FAM)和逼近理想点排序法(TOPSIS)的同时融入模糊数学理论，建立双渠道供应链协同风险的模糊评价模型；同时考虑广告促销因素和信息服务水平因素对双渠道供应链期望利润决策影响，以双渠道供应链各节点企业利益最大化为目标，建立斯坦克伯格博弈模型并用实例和数值仿真验证了该方法和模型的可行性与有效性，同时与已有研究方法进行比较，为双渠道供应链协同风险机制优化研究提供了理论指导和可行的方法借签。

1 双渠道供应链协同风险指标选择

指标选取是双渠道供应链协同风险管理的关键，也是保障供应链各节点顺利运营的前提。双渠道供应链节点企业多、地理位置分布广泛、参与环节多注定了其复杂性、广泛性的特点，再加上双渠道供应链自身混合销售渠道的特殊性，决定了双渠道供应链协同管理风险指标划分的复杂性、多样性、个性化的特点。

本研究从系统宏观的角度出发，考虑双渠道供应链是一条完整闭合的增值链，其稳定性必然受到供应线上和线下的影响，因此把双渠道供应链链上的协同风险分为内生风险，链下视为外生风险[18-19]。内生风险指供应链系统内部各要素成员之间的交替流动。这类风险主要由缺乏透明性、主导意识淡薄、JIT的不正确应用和预测决策的效率低导致。外生风险指供应链与外部环境的互动风险和人为的促销服务风险，包括信息中断、自然灾害、人员罢工突发事件、恶意破坏广告补贴率降低或中断等造成的损害[1]。上述协同风险影响因素见图2。

根据文献[20-24]，得出双渠道供应链协同风险的影响因素如表1所示：

表1 双渠道供应链协同风险影响指标

考虑双渠道供应链自身的混合性特征，表1在前人研究的基础上把原有指标融会贯通并强调人文风险、沟通协作风险、信息共享风险、促销服务风险对双渠道供应链协同的影响，可分15个一级指标和38个二级指标强化双渠道供应链的可靠性和有效性[25]，采用梯形直觉模糊数的FAM-TOPSIS法解决双渠道供应链中风险指标优化选择问题，随后对选择的重点指标进行数值模拟分析，对风险管理做出优化决策。

2 梯形直觉模糊数的FAM-TOPSIS多属性评价方法

2.1 梯形直觉模糊数的定义及运算规则

(1)

(2)

图3 梯形直觉模糊数曲线图

(1)用梯形直觉模糊数表示的语言值的加法⊕：

(3)

(2)用梯形直觉迷糊数表示的语言值的乘法⊗：

(4)

(3)用梯形直觉迷糊数表示的语言值的除法÷：

(5)

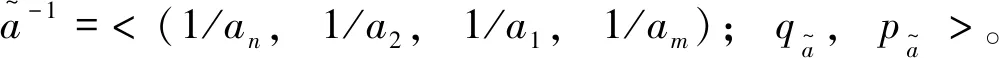
(6)

定义3[28]假设Ai(i=1,2,…,n)是一组直觉梯形模糊数集合，w=(w1,w2,…,wn)T是Ai的权重向量，则直觉梯形模糊加权平均算子(TrIFWA)定义为：

(7)

对于所有i=1,2,…,n。若wi=1/n，则TrIFWA算子退化为直觉梯形模糊算术平均算子(FrIFA)；

(8)

(b2-a2)2+(bn-an)2+(bm-am)(b1-a1)+

(b2-a2)(bn-an))]1/2。

(9)

2.2 梯形直觉模糊数的FAM-TOPSIS分析方法的评价原理

求解步骤如下：

步骤1：对评价指标进行KMO和BARTLETT统计检验，看是否适合做因子分析，确定出主要影响因素和各主导因素的权重Wi[26]。

j=1, 2,…,k；i∈B，

(10)

(11)

随后计算h(k)tj与群体平均偏好的相似度：

(12)

对每个单属性偏好信息对应的权重计算：

(13)

所有个人决策信息需要集合为群体决策信息，可以采用FrIFWA算子来进行集合

(14)

(15)

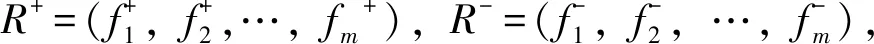
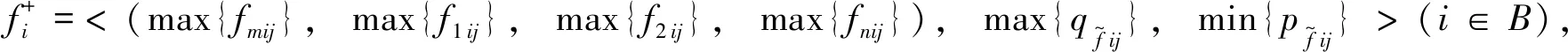
(16)

(17)

步骤6：计算各个方案Rt∈R与梯形直觉模糊正负理想方案的相对贴近度如下：

(18)

(19)

3 问题描述与期望利润模型建立

3.1 问题描述与模型符号

首先本文的研究对象是一个双渠道供应链模式，即随着电子商务、互联网等信息技术支撑的网络直销渠道与传统零售渠道相结合的情况下，采用因子分析法(FAM)和逼近理想点排序法(TOPSIS)的同时融入模糊数学理论，建立了双渠道供应链协同风险的模糊评价模型，对多属性评价指标进行降维处理，解决了双渠道风险协同评价指标融合和评价指标过硬问题；随后把提炼的重要指标选择相关性最高的两个因素来模拟分析其对供应链线上、线下的期望利润的影响；并用算例和仿真验证了该方法和模型的可行性与有效性，为双渠道供应链绩效评价和风险协同优化决策提供了一种可行的方法借签。双渠道供应链运作关系如图4所示：

图4 双渠道供应链运作图

模型变量符号如下所示：

3.2 模型构建

(1)模型假设

为确保模型构建的意义和现实性，需对模型进行如下假设：

①假定Em和Er均为正值，这样可以保障双渠道供应链协同管理的定价决策顺利运行。

②假设网络直销店和传统零售店面对的市场需求为随机变量。

③设订货周期的最标准时间为0，同时定义y≤0表示制造商在提前期内按时供货；若y>0表示制造商的延期供货时间。

④信息完全共享的及时性与准确性是双渠道供应链整体协同的基本条件。

(2)模型构建

该模型是在风险规避情况下构建的，为了实现风险协同管理这里主要引入信息共享替代因子c和制造商为零售商承担促销成本比例因子。假设网络渠道的需求比例用θ来表示，则(1-θ)为零售渠道的需求比例；且θ∈(0,1)，c∈(0,1)。信息共享特征是整个供应链的基本需求，这种情况下提前期重叠产生的风险可以大大降低。为了达到整体供应链共赢的最终目标，渠道之间需要进行合作才能实现最终目标。该模式主要靠引入的两个因子进行调节，即零售商的广告促销的投入的部分成本需要制造商在广告促销中承担，剩余部分补偿给零售商，弥补部分需求转移的损失[17]，该损失主要因网络渠道的加入引起的广告促销投入成本分摊比例为f，如若f∈(0,1)则制造商承担f·k的广告促销费用。供应链双方显示Stackelberg主从博弈，制造商和零售商的利润函数分别为：

Em=(pi-v)di+(w-v)dj-f·k，

(20)

Er=(pj-w)dj-(1-f)·k。

(21)

考虑风险规避态度下的模型构建：

maxEsc=maxEm+maxEr，

(22)

(23)

(24)

(25)

(26)

(27)

(28)

4 模型求解

4.1 风险绩效评估模型求解

广西某汽车企业从2010年到2017年对网络销售、汽车超市等汽车销售方式不断完善，并开始线上、线下同时销售的情况，以某汽车企业[31]为例，拟定从3个同行企业{H1,H2,H3}中选择一个最佳企业形成供应链协同管理的长期合作联盟。为有效解决评价指标融合问题和指标过硬问题，文章主要聘请了8位专家{M1,M2,M3,M4,M5，M6,M7,M8}组成决策小组，对双渠道供应链的风险指标进行问卷调查。采用梯形直觉模糊数的FAM-TOPSIS法确定双渠道供应链的风险绩效评价指标，并确定出最优合作企业，步骤如下：

步骤1：采用问卷调查法，分发给8位专家对供应链风险的38个指标进行打分，其中专家团队包括高校学术型专家2位，政府管理型专家2位，企业实际运营型专家2位，供应链典型代表企业专家2位，以10分制为打分原则，对双渠道供应链协同管理影响因素进行分析打分。其中，影响程度很高、较高、一般、较低、低分别代表9～10分、7～8分、5～6分、3～4分、1～2分；采用FAM法对收集的数据进行分析，首先确定该评价指标适合做因子分析，如表2和表3所示；然后提炼出主要影响因素，如图5所示能提炼出6种主成分。根据因子方差分析运行结果可以得出因子影响程度大到小的顺序排列为K42，K82，K151，K61，K11，K71，且由解释的总方差的相关系数表计算出权重系数W=(0.19，0.174，0.167，0.164，0.17，0.159)。

表2 KMO和BATLAB适度检验

图5 碎石图

表2中，KMO值为0.784>0.5，表明变量间的共同因子多，适合做因子分析；Bartlett球体检验显著水平值为0.005<0.05，表明变量间存在相关性，适合做因子分析。表3中可以选择出主要的影响指标K42，K82，K81，K151，K92，K91，K61，K71，而这些二级指标对应一级指标分别为：K4，K8，K15，K9，K6，K7。

步骤2：对选出的主要因素进行梯形直觉模糊数评价，去模糊化结果如表4所示。

表3 主成分矩阵相关系数解释的总方差

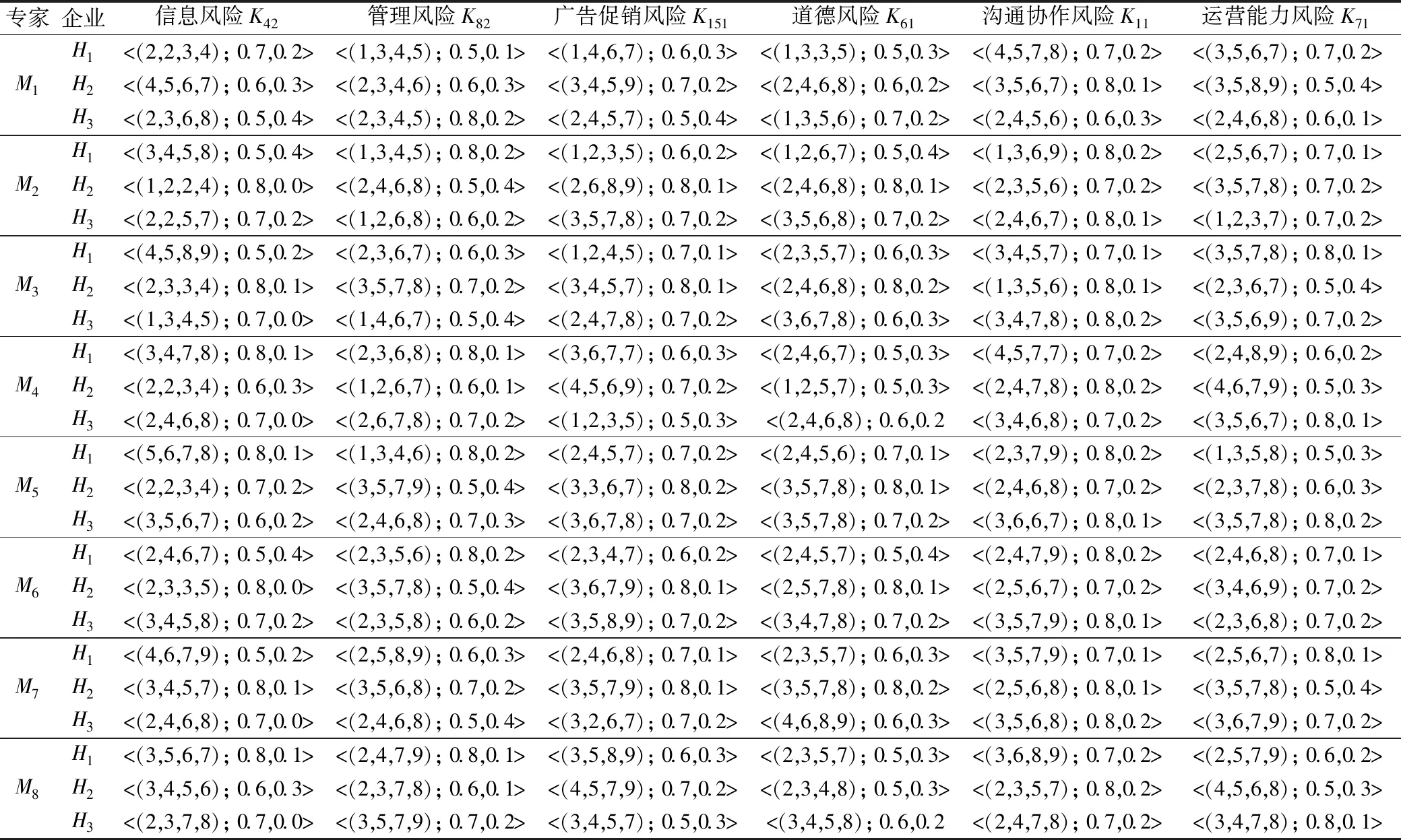
表4 梯形直觉模糊决策矩阵

步骤3: 计算决策者权重如表5所示。

表5 决策者权重

步骤4：计算企业之间的加权梯形直觉模糊数的决策矩阵，如表6所示。

步骤5：得出梯形直觉模糊数的正负理想解如表7所示。

步骤6：得到备选方案与梯形直觉模糊数的正负理想解的相对贴近度并排序比较如表8所示。

表6 集结梯形直觉模糊决策矩阵

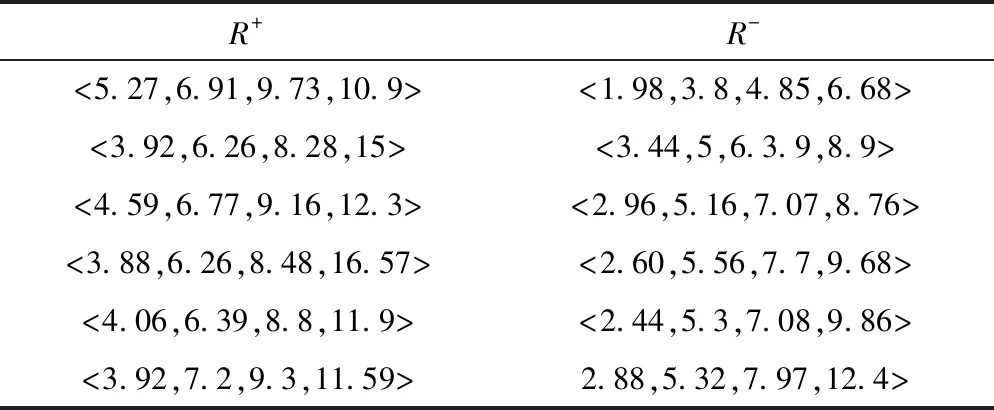
表7 梯形直觉模糊正、负理想方案

表8 方案的最优解排序比较

表8可以看出H1>H3>H2，则H1是最优的方案。相比已有的多属性决策方法[14]，本研究首先应用直觉梯形模糊数表示决策信息，同时采用FAM法对所选指标进行降维处理，选出6个主要一级指标进行计算，减少了计算量；同时在利用模糊数对决策者权重进行确定，把定性的指标定量化处理，在客观刻画决策者权重方面更为精细和准确，减小决策损失；其次利用TOPSIS法比较评价对象与正负理想解的相对贴近程度，对多属性方案进行择优排序，更加真实地反映了决策者对事物的评价和感知。

4.2 期望利润模型求解

选择上述两个指标信息共享因素和广告促销服务因素，以双渠道供应链整体利润最大为目标，对上述模型进行仿真计算，得出这两种因素如何影响双渠道供应链线上、线下的协调风险管理。假设该系统是一个由制造商和多个零售商组成的二级市场结构，参考文献[32]各参数为离散数据，其取值范围如下：

μ、δ∈(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)；

w∈(12, 18 ,22, 28, 32, 38, 42, 48, 52, 58)；

t∈(0.001v)；

ri、rj∈(0.16v，0.21v，0.26v，0.31v,0.36v)；

si，sj∈(0.15v,0.35v,0.50v,0.65v,0.8v)；

v∈(16,21,26,31,36)；

a∈(100, 200, 300, 400, 500)；

θ，λ，c，f，w∈(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0)；

τ∈(12, 22, 32, 42, 52)；k∈(20)。

其中k的值相对选大，能反映促销服务补贴率的重要性。

采用Matlab编程对如上期望利润模型进行仿真分析，结果如图6所示：pi、pj在图(a)、(b)中分别表示z轴，ξ代表图中的y，c代表图中的x。

图6 pi和pj随着ξ和c的变化

pi、pj随着信息共享替代因子c和交货提前期重叠的影响因子ξ的变化而变化，当ξ一定时，pi随着替代因子c的增加而提高，而pj随着ξ和c的增大而降低，并与Pi交会，随着网络渠道客户的增加，零售渠道的客户就是转移到网络渠道，要想实现共赢，零售渠道必须提高售价。相反，pj随着ξ和c的减小而增加。

对Qr、g和τ做仿真练习，结果如图7所示，图中x，y，z轴分别代表τ，g和Qr。

图7 Qr随着g和τ的变化

图7可以看出当g不变，Qr随τ的增加而增加；同理当τ不变，Qr随g的增加也在增加，说明可以通过增加订货量来减小波动引起的缺货风险。

对参数赋值，通过数值仿真来计算出信息共享和广告促销服务因素对零售商、制造商和供应链总利润的影响，如图8、图9所示。

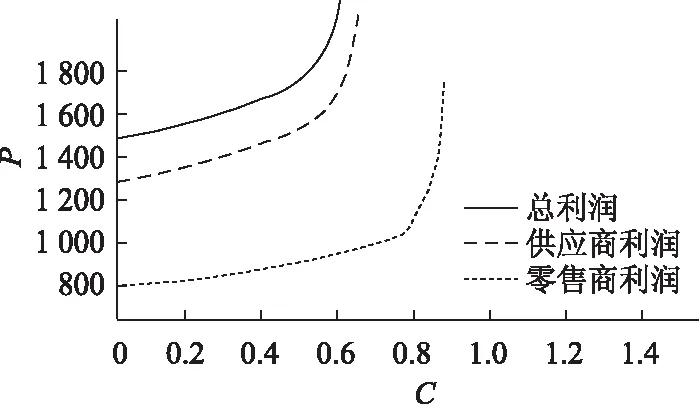
图8 信息共享因素对供应链利润的影响

图8可以看出随着信息共享替代因子的增加，零售商和制造商的利润会显著增长，且零售商的利润小于制造商的利润；信息共享下的总利润水平都要大于各种的利润。

图9 广告促销因素对供应链利润的影响

图9可以看出随着广告促销投入的增加，零售商、制造商的利润会有所增长，并且零售商的利润总体要小于制造商的利润。因为随着广告投入的增加，产品的批发价格有所减少，制造商的利润就会增加。总体趋势来看，供应商的总利润大于制造商和零售商单独的利润，因此在广告促销投入力度增大时，总的供应链利润水平也会增加。对比图8可以得出信息共享投入远比广告投入所导致的利润增速快，可见政府部门和各节点企业要增加信息共享投入比例。

5 结论

文章对T-JIT环境下双渠道供应链线上、线下的风险协同优化进行研究，首先结合模糊理论提出基于梯形直觉模糊数FAM-TOPSIS的多属性决策评价方法来解决风险评价指标融合困难和权重确定“过硬”问题；同时根据风险评价选出的两个最重要的影响因素，以双渠道整体利益最大化为目标，应用stackelberg博弈理论建立期望利润决策模型，并用仿真与算例分析得出如下结论：

(1)全面准确地确定出双渠道供应链风险指标影响因素，利用梯形直觉模糊数的FAM法对多属性指标进行降维处理并选择出主要的影响因素和权重，同时用TrIFWA算子和直觉梯形模糊数期望值计算决策者的期望权重。

(2)引用算例采用TOPSIS法计算梯形直觉模糊正负理想方案的相对贴近度排序，总结出最优的风险控制管理企业，同时可为企业进一步优化风险管理做出正确决策。

(3)双渠道供应链协同合作整体利润最大化的前提下，信息共享率增强时，制造商和零售商都能提高产品销售量，定价比较透明；当制造商信息共享替代性增强时，制造商会提高定价，零售商会降低售价来吸引顾客，促使利润从制造商流向零售商来达到平衡。

(4)供应链各主体和政府部门要加强信息共享和广告促销服务的投入比例，才能保证各节点企业整体利润最大化，提高供应链线上、线下物流中断的风险水平。

本研究为不确定风险环境下双渠道供应链企业正确识别、评价和选择供应商提供理论参考和方法借签，在未来研究中，可以综合考虑风险偏好和绿色度偏好程度等因素对供应链风险弹性的影响，进一步研究双渠道绿色供应链的利润和定价决策问题。