基于DAE-HTPF的新能源汽车电池剩余寿命预测
2020-03-25
(1.宁夏大学新华学院,宁夏 银川 750021;2.宁夏大学土木与水利工程学院,宁夏 银川 750021)
0 引言
新能源汽车车载电池在使用过程中,电池的某些性能参数退化会引起不良后果,如当电池容量退化到达一定阈值时,电池的寿命就将终结[1]。因此,在电池使用过程中,有效地提取锂电池的性能退化趋势特征,准确地预测电池剩余寿命,及时地调整汽车控制策略,可极大地提高车辆的使用体验,且降低成本。可见,锂电池的剩余寿命预测对新能源汽车的推广有着重要影响[2-4]。
目前,针对复杂电子系统的锂电池剩余寿命(remaining useful life,RUL)的预测主要集中在2个方面:一是通过检测电池的整个生命周期性能退化参数,来实现预测。这种方法虽然能获得较为丰富的样本数据且容易实现,但考虑到电池的性能退化是一个长期的过程,而且某些场合很难进行数据采集,如太空车的车载电池等[5]。二是在线RUL预测。这种方法能对锂电池进行预测性维护,且能对控制系统提供决策信息,如对于可维修电池来说,依据RUL预测结果可对其进行维修或更换[6]。其中,在线RUL预测方法应用最为广泛,且这种方法易于将模型与数据驱动结合起来,从而能更加有效地实现RUL预测。
研究表明,PF是基于模型实现产品剩余寿命预测的理想方法之一[7-9]。而对于锂电池的寿命预测来说,通常将电池容量、放电深度和循环次数等作为观测值进行分析。但是,考虑PF所建立的状态方程比较单一,不能较好地适应电池退化趋势,也不能完全表征具备一定随机性的电池退化趋势,且存在提取电池退化过程中的信息特征仍需借助人们经验、成本较高等问题。与此同时,深度学习能自动从大量样本数据中获得数据特征,避免人为因素,也解决了机器学习的不足[10]。根据以上分析,提出一种基于DAE与HTPF的电池剩余寿命预测方法。该方法能有效地对电池退化过程中的信号特征进行收集与自提取,而且将趋势性特征作为训练集输入到DAE中,在此过程中无需人们经验;且通过HTPF方法优化了各阶段状态方程的参数,解决了单一状态方程无法表征这一致命问题。
1 基本原理与算法流程
1.1 HTPF原理
由于锂电池在退化过程中具有很大的不确定性和随机性,因此无法用一个确定的函数来表征任一锂电池退化趋势[11]。本文将拟合误差平方和为最小时的目标函数作为状态方程,这种状态方程中的参数会随着锂电池退化衰减趋势的变化而变化,以满足当前条件下的锂电池退化趋势要求。
具体流程如下:
a.程序初始数据,令i=1。
b.输入n(n为非零自然数)个单次拟合状态方程时所需的电池退后信号特征值,进行数据拟合,把平方误差和最小时的函数作为PF状态方程。
c.利用PF算法对上述状态方程中的参数进行优化,并确定电池退化趋势,通过设定阈值计算电池的剩余寿命。
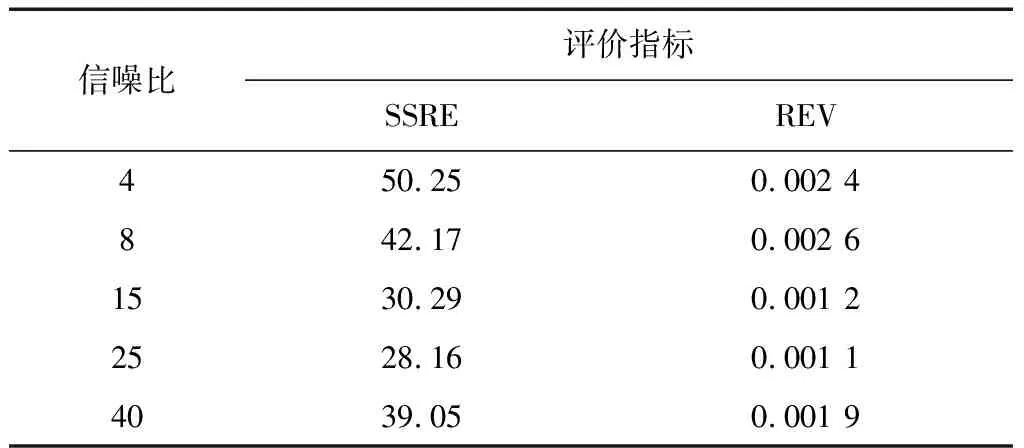
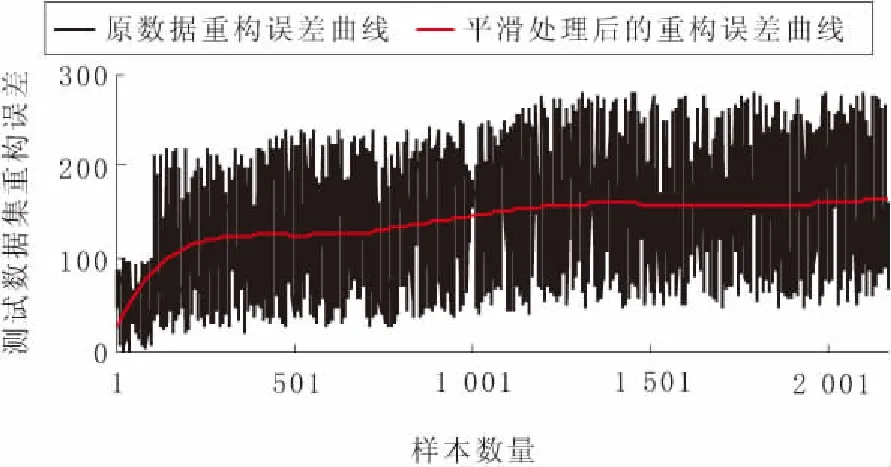
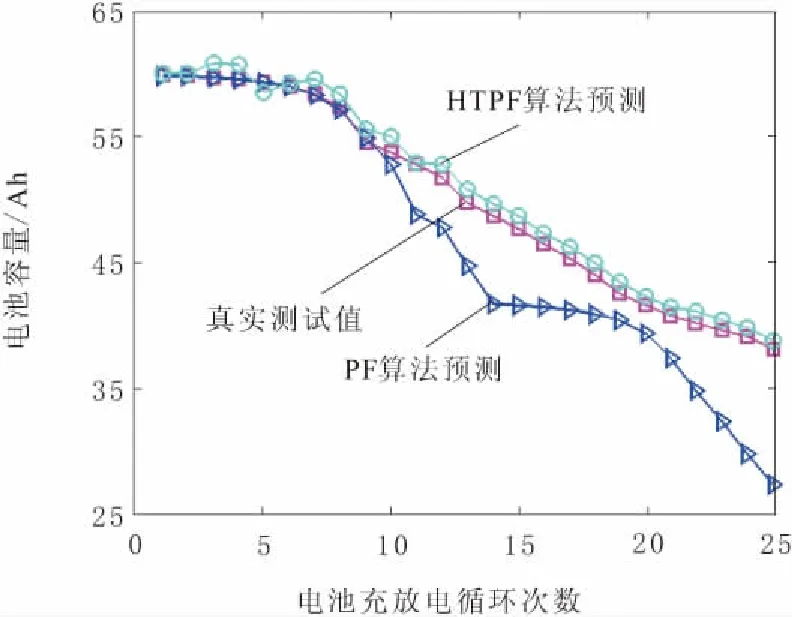
d.额外增加m个(m 在使用降噪自编码器训练数据的过程中,传统意义上的特征输入无法将电池使用全周期的特征进行归一化处理,而归一化处理对于神经网络来说又至关重要。因此,本文考虑到电池在使用过程中出现退化的样本很可能会受到不确定因素的影响而缺少,甚至出现样本数据少于特征数量的状况,这必然导致算法出现过拟合状况,所以需要对训练数据进行加噪[12]处理来扩展数据空间,以达到更好的拟合效果。 本文基于DAE-HTPF的电池剩余寿命预测算法流程如图1所示。 图1 电池剩余寿命预测算法原理 本文的新能源车车载动力锂电池数据来源于CALCE,且由于原始数据的数量庞大,为了简便运算,对其采用分段平均的前置处理。共采集有2 167组数据,其中,1~150组数据经过加噪处理作为训练集数据,将151~2 000作为测试集数据,将2 001~2 167组数据作为阈值设定样本。为了更好地对比算法的有效性,本文设置了PF和HTPF 2种算法,对新能源汽车车载电池的剩余寿命进行了预测。本文添加4,8,15,25,40等5种信噪比的高斯噪声。 本文利用相对误差平方和(sum of square of relative error,SSRE)与相对误差方差(relative error variance,REV)2种指标,来评价验证集误差曲线的平滑性。 基于不同信噪比的验证误差曲线平滑性指标如表1所示。可以发现,当信噪比为15和25时,验证误差与提出的曲线拟合平滑性指标达到较小值,从而得出的重构误差曲线是最平滑的。因此在无法得到电池全周期的信息特征情况下,利用测试误差来优化参数是能够保证重构误差的平滑性的,也就是说当需要提取电池出现轻微退化或完全退化时的少量信号特征时,能实现电池退化趋势性的信号特征自提取。 表1 不同信噪比下的曲线平滑性评价指标 由以上分析可知,将2 001~2 167组数据输入到降噪自编码器中,求得容量阈值为46 Ah,将其作为测试集重构误差曲线阈值。为了进行平滑处理,现从重构误差中每100个数据求取平均值作为1个新的预测值,原数据和平滑后的重构误差曲线如图2所示。 图2 重构误差曲线 本文取HTPF算法初始化的参数为n=25,m=2。将进行平滑处理后的重构误差依次作为HTPF算法的输入,并计算相应状态方程拟合得到的预测值,计算离散化后的数值与真实值之间的差平方和,选择其最小时的函数作为此阶段的状态方程,拟合得到优化后的参数。此后重复上述过程,依次得到25组拟合后的状态方程。结合上述状态方程与PF算法实现电池剩余寿命的预测,预测的结果如图3所示。横坐标表示锂电池充放电循环次数间隔,纵坐标表示电池容量。 图3 锂电池剩余寿命预测 由图3可知,HTPF算法所预测的结果更加接近真实测试值,说明该方法能更好地发掘电池退化的趋势性变化,从而适时地优化状态方程参数。结果表明,HTPF算法较PF算法具有更高的精度,鲁棒性更强。 利用DAE-HTPF算法对新能源汽车车载动力电池的剩余寿命进行了预测,该算法能有效地避免人为因素的干扰,节约预测成本。另外,该方法对锂电池退化趋势能做出很好的判断,使状态方程的参数能够适时调整,以达到最佳的预测效果。1.2 特征提取
1.3 算法原理
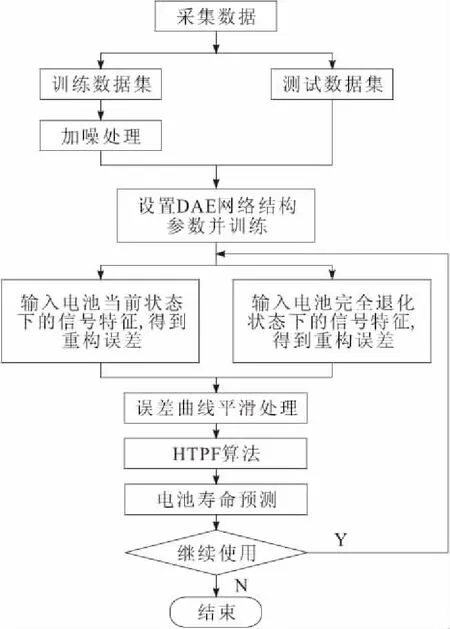
2 分析与讨论
3 结束语
