PMSM分数阶模型参考自适应调速系统研究

任金霞，黄艺培，蒋梦倩

(江西理工大学 电气工程与自动化学院，江西 赣州 341000)

0 引 言

永磁同步电动机(permanent magnet synchronous motors，PMSM)由于其高效率、低惯性和高转矩惯量比等高性能特性而在工业中得到广泛应用。在许多应用中，PMSM的快速响应和高精度转速控制都是重要的技术指标。

永磁同步电机一般用传感器来检测转子的位置和转速，但这会降低永磁同步电机的鲁棒性。在很多环境下，传感器并不可靠，反而会增加系统的复杂性并可能导致电磁干扰问题，无传感器方法则可以避免这些问题。目前有许多估计永磁同步电机转速的技术方法，如高频注入法和扩展卡尔曼滤波器(EKF)技术。但是这些技术方法的使用都要经过大量复杂的信号处理运算，这增加了计算的难度和系统的复杂度。通过分析发现，模型参考自适应控制(model reference adaptive control，MRAC)技术能够有效地解决这些问题。MRAC是用于估算转子速度和位置最好的技术之一，由于其在性能方面需要较少的计算时间，因此易于实现。但是MRAC一般适用于低速且精度要求不高的场合[3]。

为提高系统的鲁棒性，本文提出将分数阶理论应用于模型参考自适应系统中，在同步旋转坐标系中根据PMSM的电流方程建立可调模型和参考模型，并以参考模型和可调模型的d-q轴电流差值作为误差，转速作为可调参数，根据分数阶Lyapunov稳定性理论设计分数阶自适应律。在MATLAB/Simulink环境下进行仿真实验，实验结果显示，分数阶自适应律应用于模型参考自适应系统具有明显优越性。

1 分数阶微积分

分数阶微积分实际上是任意阶微积分，阶数甚至可以为复数[4]。分数阶微积分算子定义为

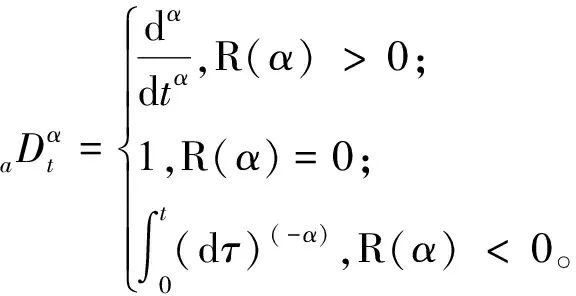
(1)

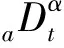
在分数阶理论的发展过程中，出现了多种定义，最常见的R-L分数阶积分定义为

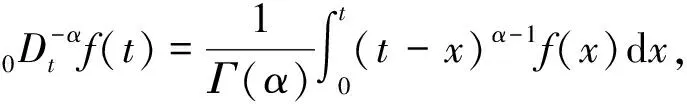
(2)

式中：t>0，α∈R+；Γ(α)为Gamma函数，

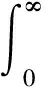
(3)

2 PMSM模型参考自适应系统

本文以永磁同步电机的电压和电流作为自适应控制系统的输入，根据参考模型和可调模型的输出电流误差得到转速误差信息，由此设计分数阶自适应律。分数阶MRAC设计框图见图1。

图1 分数阶MRAC设计框图

2.1 参考模型和可调模型

表贴式三相PMSM在同步旋转坐标系下的电压方程为

式中：ud,uq,id,iq分别为同步旋转坐标系下定子的d-q轴电压和电流；Ls为d-q轴定子等效电感；ωe为电机转速；ψf为磁链；R为定子电阻。

将式(4)写成电流方程的形式：

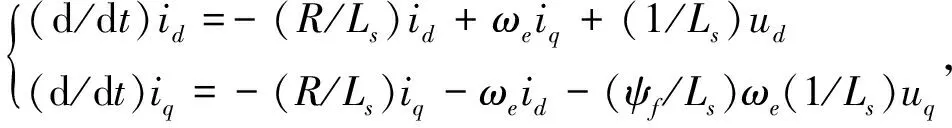
(5)

令

则式(5)可变换为

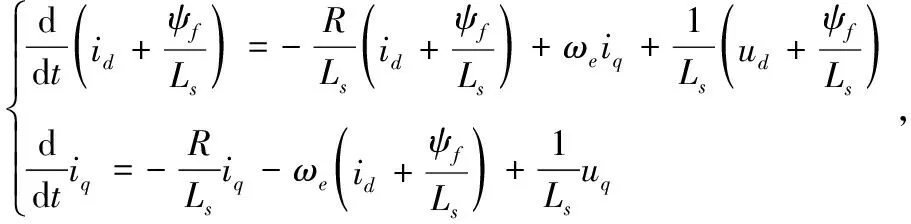
(7)

式(7)可简写为

(8)

将式(8)写成状态空间表达式

(d/dt)i′=Ai′+Bu′，

(9)

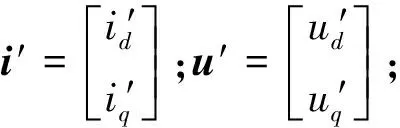
式(9)中的状态矩阵A包含转子速度信息，因此可将此式作为可调模型，ωe为可调参数，三相PMSM为参考模型。

将式(8)以估计值表示为

(10)

式(10)可简写为

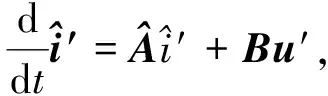
(11)

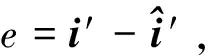
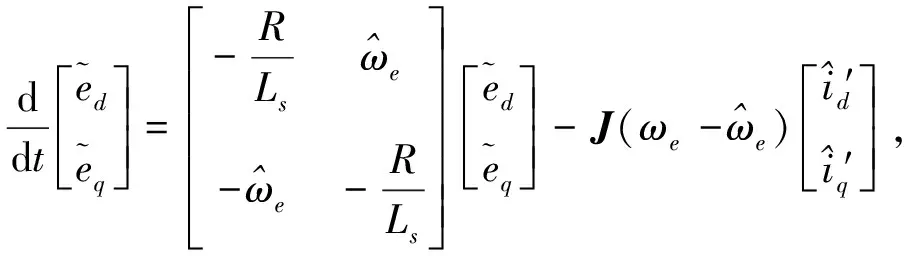
(12)

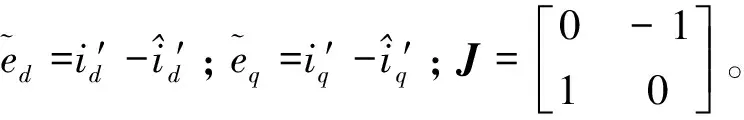
将式(12)写成

(13)

2.2 分数阶Lyapunov稳定性理论

考虑到电机中的电容和电感都具有分数阶特性，引用文献[5]中的分数阶Lyapunov稳定性定理，此处不再证明。

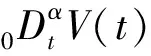
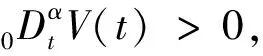
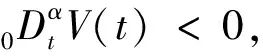
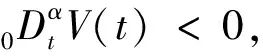
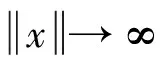
2.3 分数阶自适应律的设计

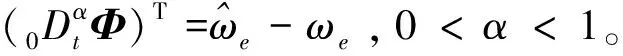
则式(13)可表示为

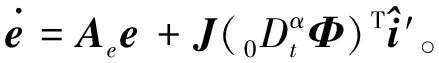
(14)

设计Lyapunov函数为

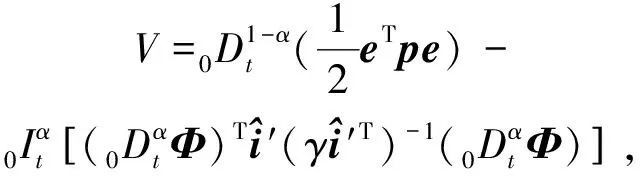
(15)

其中，系数γ>0。

对式(15)求α阶导，得

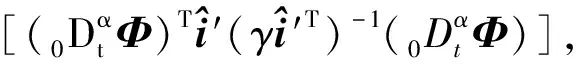
(16)

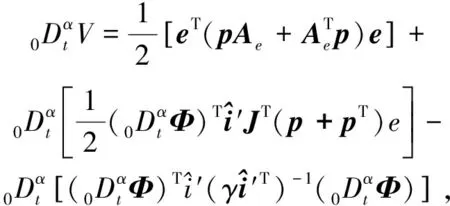
(17)

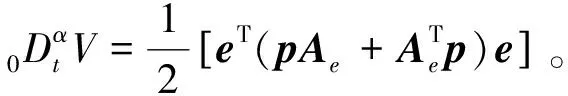
(18)

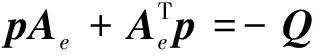
令p为单位阵，则

可得

设KI=γ，为提高系统的响应速度，引入比例环节，则

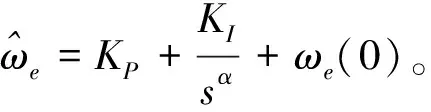
(21)

3 仿真实验与结果分析

按照图2所示的PMSM无传感器矢量控制框图，在MATLAB/Simulink环境下搭建仿真模型。其中，电机的仿真参数如表1所示。

图2 基于分数阶MRAC的PMSM矢量控制框图

将自适应律的参数值设为KI=0.5，KP=0.3，α的取值约束在[0.1，1]间，经过多次实验，发现当分数阶次取α=0.1时，能取得较好的控制效果。为了分析分数阶模型参考自适应系统具有的动态性能和稳态性能，与传统整数阶模型参考自适应系统得出的仿真结果进行对比如下。

3.1 电机在空载状态下的响应

电机在空载状态下启动，给定转速为300 r/min,仿真结果如图3和图4 所示。

3.2 转速突变时的电机响应

电机在空载状态下启动，给定转速为300 r/min，在0.3 s时转速突变为650 r/min，仿真结果如图5和图6所示。

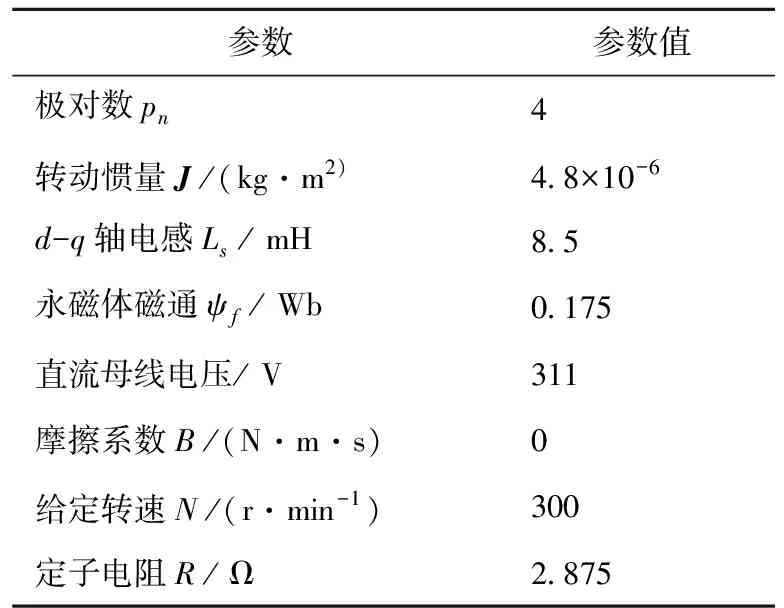
表1 电机仿真参数

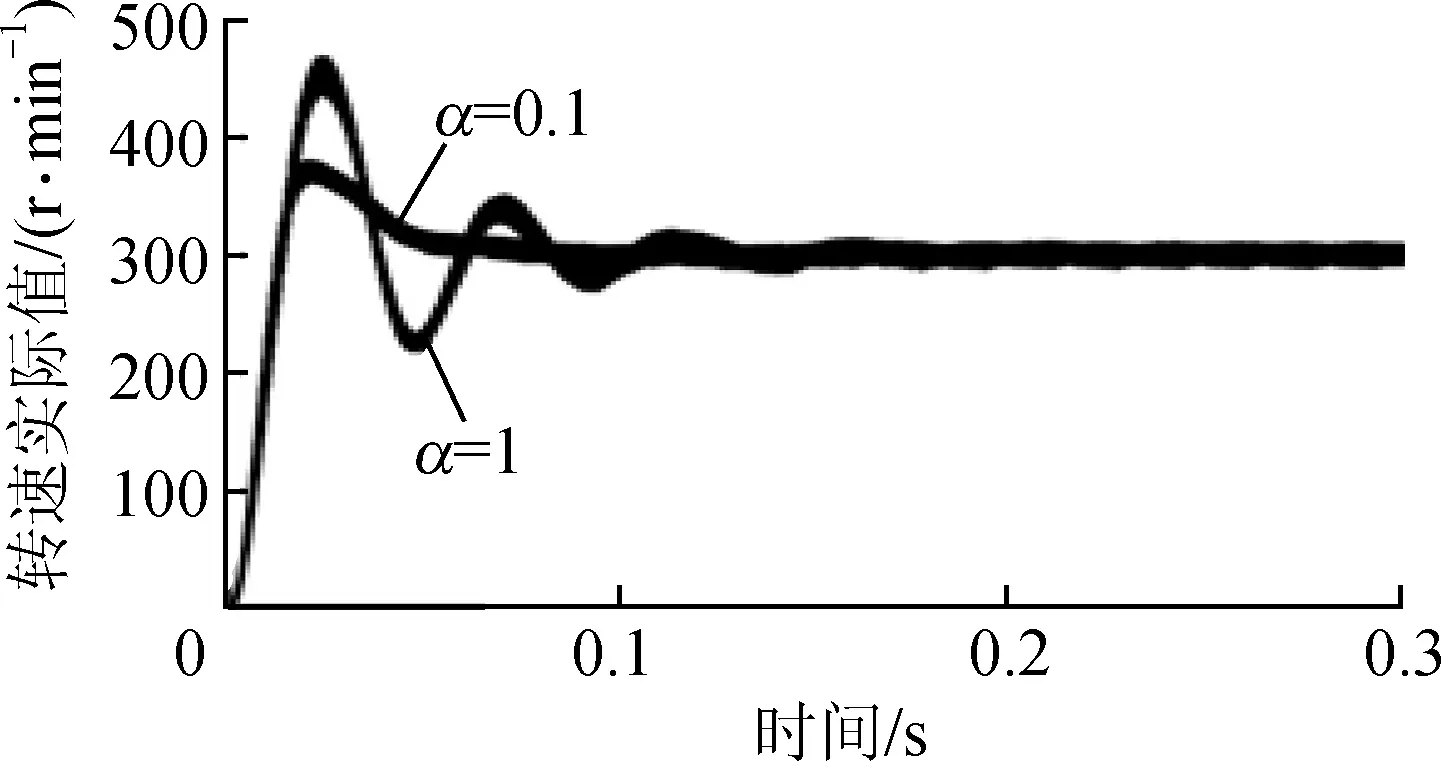
图3 电机实际转速

图4 电机转速估计误差

3.3 加入5 N负载时的电机响应

电机在空载状态下启动，给定转速为300 r/min，在0.3 s时加入5 N负载，仿真结果如图7和图8所示。

从图3和图4中可以看到，对于PMSM的转速实际值，当α=0.1时电机转速能够快速响应，且相比于整数阶，有较小的超调量，调节时间短，在0.05 s左右能快速达到稳定状态，而整数阶情形下则需要0.18 s左右达到稳定状态。在分数阶情形下，系统进入稳定状态的时间仅为整数阶情形下的27.8%。

从图5～6中可以看到，在转速突变的情况下，α=0.1时电机转速可快速达到650 r/min，能够在0.36 s左右迅速达到稳定状态，并且在转速突变时，转速估计误差稳定在10 r左右。而当α=1时，电机在0.4 s左右才能进入到稳定状态，

图5 转速突变时电机实际转速

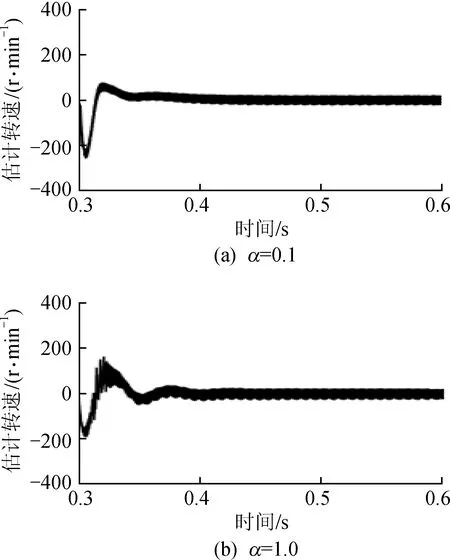
图6 转速突变时电机转速估计误差

耗时较长，且转速估计误差稳定时抖动较大，为20 r左右。在分数阶情形下，系统进入稳定状态的时间提高了50%，转速估计精度提高了50%。

从图7～8中可以看到，当系统加入负载时，在整数阶情形下，电机实际转速会受到较大的扰动，在0.3 s时最大转速为470 r左右。而当α=0.1时，电机实际转速受到的扰动较小，在0.3 s时最大转速为400 r左右，然后迅速回到稳定状态，最大转速估计误差降低了29.4%，有较强的抗扰动能力。

从以上仿真结果可以看出，相比于整数阶自适应律情形下，PMSM在分数阶自适应律情形下调速性能得到了提高，有较好的鲁棒性。

图7 加入负载时电机实际转速

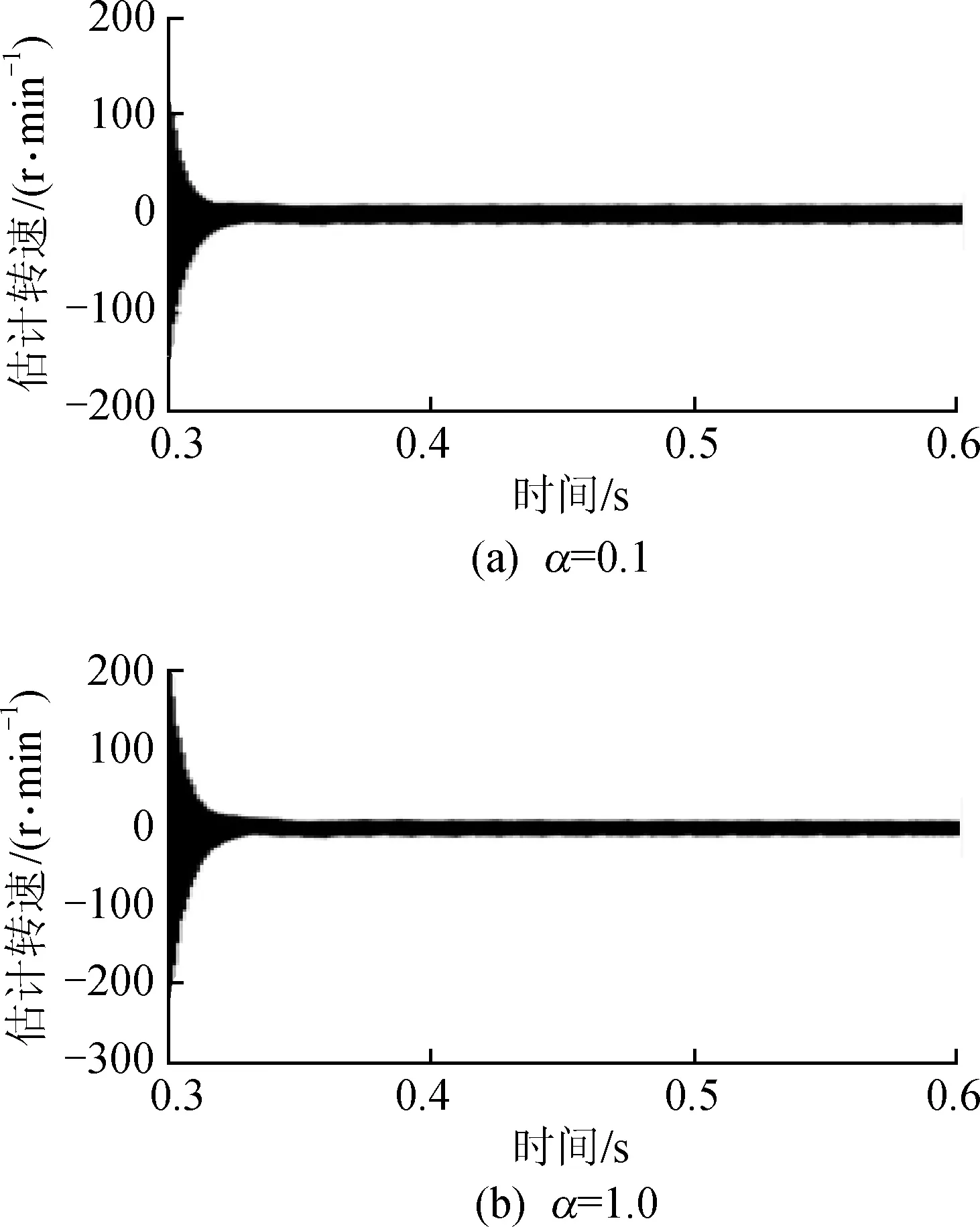
图8 加入负载时电机转速估计误差

4 结 论

本文提出了一种基于Lyapunov稳定性理论的分数阶MRAS方法并应用于PMSM中。将PMSM本身作为参考模型，PMSM电流方程作为可调模型和适应机制，为获得更精确的转速，将分数阶理论应用于自适应律中。仿真结果表明，相比于整数阶情形，在分数阶情形下，电机调速系统能够有较好的动态响应和较好的鲁棒性。