高温气体效应对高超声速磁流体控制的影响

丁明松,刘庆宗,江涛, 高铁锁,董维中,傅杨奥骁

中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000

20世纪90年代以来，随着计算机技术、等离子体技术和超导磁体技术的蓬勃发展，面向高超声速飞行器的磁流体控制研究掀起热潮[1]。利用机载磁场向高温气体流场注入适当的动量和能量，改变高超声速飞行器绕流流场特性，这就是高超声速磁流体控制。它可以有效改善高超声速飞行器的气动特性，在飞行器气动力操控、气动热环境管理和等离子体分布调节等方面具有广阔的应用前景[2]。

数值模拟是研究高超声速飞行器磁流体控制的主要方法之一。要准确模拟高超声速磁流体流动，首先依赖于高超声速飞行器高温气体流场等离子体分布的准确获得，它是高超声速磁流体控制数值模拟研究的基础。对于高超声速飞行器，如果飞行速度较高，强烈气动加热会使气体发生离解、电离等化学反应，分子热力学温度内能模态不同程度激发，即出现高温气体效应[3]，对高温气体流场特性会造成严重影响[4]，进而影响高超声速磁流体控制效果。

随着流动时间尺度的变化，高温气体效应存在冻结、非平衡和平衡3种流态[3]，不同流态高温气体流动的模拟，常依赖于各种气体模型进行。完全气体模型忽略了化学反应和分子热力学温度激发对气体性质的影响(即气体处于化学反应和热力学冻结状态，也可认为是忽略高温气体效应影响)，比热比保持恒值不变，是一种理想化气体模型。由于其处理相对简单，因而广泛应用于各类飞行器流场的数值模拟。平衡气体模型是一种模拟高温气体化学反应的简化模型。其主要思想是，假设流场中气体微元处于热力学和化学反应的平衡态，此时气体组分、内能、焓等状态参量都只是温度和压力的函数。该模型能在一定程度上模拟高温流场中热化学现象的极限状态。

由于高超声速飞行器流场中，各区域流速存在很大差异，冻结、非平衡和平衡3种流态往往同时存在[3]，很难准确界定区分。因此要模拟较为真实的物理环境，还需采用能自动模拟平衡/非平衡/冻结3种状态的非平衡气体模型。常用非平衡气体模型有化学非平衡气体模型和热化学非平衡气体模型[3]。化学非平衡气体模型主要考虑化学反应的非平衡效应，此时热力学温度各能量模态处于平衡状态(即热力学平衡)。要同时考虑化学非平衡效应和热力学非平衡效应，则需采用更为全面的热化学非平衡气体模型。

国外在高超声速飞行器磁流体控制方面，各类气体模型均有不同程度的应用。例如，2006年，Otsu等[5]采用完全气体模型数值分析了不同条件下磁场对驻点线温度分布的影响；2009年，Boettcher[6]采用完全气体模型对球头高超声速磁流体控制Hall效应影响进行了数值计算研究；2010年，Lee等[7]采用平衡气体模型开展了磁场对激波脱体距离影响的研究，并与无磁场时完全气体(文中标识Frozen)模型的计算结果进行了比较，发现采用平衡气体模型，激波脱体距离较小，波后温度远远低于完全气体结果；2010年，Bisek和Boyd[8]采用完全气体模型开展了球柱模型的磁流体控制及其热环境研究；次年，Bisek和Poggie[9]又采用热化学非平衡气体模型(焦耳热振动能量比为0.75)，开展了钝椭圆锥体的磁流体控制数值计算分析；2012年，Nagata等[10]采用完全气体模型对弱等离子体磁流体控制进行了研究；2015年，Masuda等[11]采用化学非平衡气体模型对三维钝锥体磁流体气动力、热控制进行了研究；2016年，Fujino和Takahashi[12]采用热化学非平衡气体模型(焦耳热振动能量比为1.0)模拟了火星大气磁阻力伞效应；同年，Balsara等[13]开展了完全气体模型磁流体控制方程黏性矢量分裂方法研究。以上这些研究，在开展磁流体数值模拟时，均采用单一的气体模型，缺乏气体模型对磁流体控制影响的分析；尤其是采用完全气体或平衡气体模型时，忽略了高温气体非平衡效应的影响，其结果、结论的准确性仍有待商榷。

国内在高超声速飞行器磁流体控制研究方面起步稍晚，也有不少有价值的研究。例如2008年，田正雨[1]采用平衡气体模型对球头磁控热防护进行了数值计算分析；2009年，黄富来和黄护林[14]对比分析了完全气体模型(文中称为冻结流)和化学非平衡气体模型对高超声速弱电离气体流动的影响；2013年，黄浩等[15]采用完全气体模型对电子束电离的高超声速磁流体发电机进行了研究；2014年，卜少科和薛雅心[16]采用完全气体模型对磁控系统的热环境和阻力特性进行了研究；2016年，李开等[17]采用完全气体模型对高超声速飞行器3种磁场磁控热防护系统进行了研究，2017年又采用热化学非平衡气体模型(焦耳热振动能量比为0.5)开展了磁控热防护系统高温流场与电磁场耦合计算方法研究[18]；2018年，姚霄等[19]采用完全气体模型对外加磁场下的高超声速半球体流场进行了数值模拟。

可以看出，尽管高超声速磁流体控制研究得到了很大的发展，但大多直接选用某种气体模型进行，很少见到详细分析不同气体模型及高温气体效应对高超声速磁流体控制数值模拟影响的研究；在考虑热力学效应时，大多针对单一的焦耳热振动能量配比，热力学非平衡效应及焦耳热能量配比对磁流体控制影响规律尚不明确，需要进一步研究分析。

作者团队对高超声速飞行器非平衡流场特性及磁流体控制进行了较为广泛的研究[20-22]。本文在此基础上，主要针对上述不同高温气体模型，开展高超声速高温气体电磁流动数值研究，较为系统地分析高温化学非平衡效应、热力学非平衡效应及焦耳热振动能量配比等对高超声速磁流体控制流场特性、气动力/热特性的影响。

1 流动控制方程及其数值离散

高超声速飞行器高温气体流场中混合气体的电导率一般较低[10]，通常满足低磁雷诺数假设(Rem≪1)。此时，相对于外加磁场，感应磁场很小，基本可以忽略。流场控制方程右端出现电磁源项，其无量纲形式为

(1)

完全气体守恒变量为

Q=[ρ,ρu,ρv,ρw,ρEt]T

化学非平衡气体或平衡气体守恒变量为

Q=[ρj,ρ,ρu,ρv,ρw,ρEt]T

热化学非平衡气体守恒变量为

Q=[ρj,ρ,ρu,ρv,ρw,ρEt,ρEv]T

式中：ρj为组分j的密度；u、v、w分别为直角坐标系x、y、z方向速度；Et为气体的内能；Ev为气体的振动能；Re为无量纲雷诺数；F、G、H与FV、GV、HV分别为3个坐标方向的无黏向量与黏性向量；W和WMHD分别为非平衡源项和电磁作用源项。

方程(1)中，无黏项离散采用AUSMPW+(Advection Upstream Splitting Method by Pressure-based Weight functions)格式，黏性项离散采用中心差分格式，时间离散为LU-SGS(Lower-Upper Symmetric Gauss Seidel)隐式方法，数值计算格式和方法详见文献[3,22]。

2 气体模型

2.1 完全气体模型

完全气体模型假设高温气体处于冻结状态，忽略化学反应和热力学效应影响。此时，对于双原子分子为主的地球大气，其比热比为1.4，方程(1)中非平衡源项W为零向量，电磁作用源项WMHD为

WMHD=Qm[0,(J×B)x,(J×B)y,(J×B)z,J·E]T

(2)

式中：Qm为磁相互作用数；J为电流密度；B为磁感应强度；E为电场强度。

2.2 化学非平衡气体模型

考虑高温空气中发生化学反应，由于流场各区域流动特征时间存在数量级差别，流场中往往同时存在化学平衡、非平衡和冻结3种状态。因此需采用化学非平衡气体模型，它可以自动模拟这3种流动状态。

(3)

WMHD=Qm[0j,0,(J×B)x,(J×B)y,

(J×B)z,J·E]T

(4)

2.3 平衡气体模型

假设化学反应的特征时间远远小于流动特征时间，流场中化学反应将处于平衡态，化学非平衡气体模型将退化为平衡气体模型。

为了减小计算方法带来的误差，本文平衡气体模拟同样采用11组分空气化学反应Park模型和热力学一温度模型，这与2.2节化学非平衡气体模型保持一致，因此其源项W和WMHD均与2.2节的相关表达式一致。不同的是，在数值模拟时，采用同比例放大化学反应正反应和逆反应速率的处理方法。这种处理，不改变化学反应平衡常数，随着放大因子(η)不断增大，化学反应的特征时间逐渐减小，化学反应逐渐趋向于平衡态。当η足够大时，化学反应的特征时间足够小，流动可认为处于化学平衡态。本文取η=109，此时流场近似处于化学平衡态。

2.4 热化学非平衡气体模型

对于化学非平衡气体模型，如果进一步考虑流场中各区域热力学平衡、非平衡和冻结过程，即同时考虑化学非平衡效应和热力学非平衡效应，则化学非平衡气体模型将转变为热化学非平衡气体模型。

为了与2.2节一致，化学反应模拟同样采用11组分Park反应模型。不同的是，采用热力学双温度模型和振动-离解耦合模型[3]，模拟热力学振动非平衡松弛过程及其与化学离解反应耦合影响。方程(1)中，非平衡源项为W=[wj,0,0,0,0,0,wv]T，wv为热力学振动非平衡能量源项，其表达式为

(5)

电磁焦耳热作用部分能量将作用于振动能量项，其电磁作用源项WMHD可写为

WMHD=Qm[0j,0,(J×B)x,(J×B)y,(J×B)z,

J·E,γJ·(E+V×B)]T

(6)

式中：γ为焦耳热振动能量比，γ=0～1;V为速度矢量。

3 其他配套计算模型和方法

3.1 电场泊松方程求解

等离子体近似满足电中性假设，电流密度J满足连续性方程：

(7)

式中：J可由广义欧姆定律得到，即

J=σ(E+V×B)

(8)

其中：σ为气体电导率。

(9)

耦合方程(1)和方程(9)，数值求解得到电势函数φ和电场E，再由方程(8)得到电流J。

3.2 电导率计算

采用国外较为常用的等离子体电导率模型，主要基于分子运动碰撞理论，考虑电子、离子在等离子体中碰撞和迁移过程，得到混合气体电导率。它综合考虑了弱电离与强电离导电机理以及不同气体组分差异的影响，较为贴近混合气体等离子体导电机制，其表达式为[12]

(10)

(11)

当s为中性粒子组分时，其表达式为

(12)

σ≈2.7×105Xe

(13)

式中：Xe≤10-2。

电子摩尔分数由拟合公式[24]给出：

(14)

式中：th为双曲正切函数；ε=10-9;T0=3 000 K；D=3 000 K；X0=0.002。

3.3 磁流体气动力特性计算

对于不考虑电磁作用的飞行器来说，一般情况下，气动力系数计算仅需考虑飞行器表面压力和黏性应力的面积分。而对于高超声速磁流体控制来说，还需进一步考虑洛伦兹力的体积分。磁流体阻力系数为

(15)

式中：FM为气体洛伦兹力阻力密度(其反作用力作用于磁场发生装置，即磁阻力)；FM0为磁阻力空间积分；CD为总阻力系数；CD1为阻力系数中压力和黏性应力分量；CD2为阻力系数中磁阻力分量；α为飞行迎角；q∞和Sref分别为动压和参考面积。

4 数值方法验证

这里仅给出高超声速磁流体控制气动力特性方面的校验，更多其他方面的校验可参考作者以往的部分工作[22,25-26]。计算外形为球柱外形，头部半径为1 m，身部柱体长10 m。计算条件为来流压力5.42 Pa，来流温度220.0 K，来流马赫数为21.8，壁面温度设为2 000.0 K。采用磁偶极子磁场，磁场感应强度计算方法为

(16)

式中：(r,α)为极坐标单位矢量；磁场配置于头部，其中心与球心重合；特征点磁感应强度B0=0.2 T，磁场特征长度r0=1.0 m；磁场极轴与球柱轴线的夹角θ，见图1。

图1 磁场配置示意图

由于高温产生等离子体，等离子体在磁场中运动产生感应电流(图2)，感应电流在磁场中受洛伦兹力作用，形成磁阻力伞，改变飞行气体的阻力特性。表1给出了磁场不同倾斜角度时钝柱体阻力系数。可以看出，磁场配置对飞行器阻力特性的影响较为明显；不同磁场条件下，本文计算的阻力系数，均与文献[10]符合较好，其差异小于0.5%。

图2 环形电流密度大小

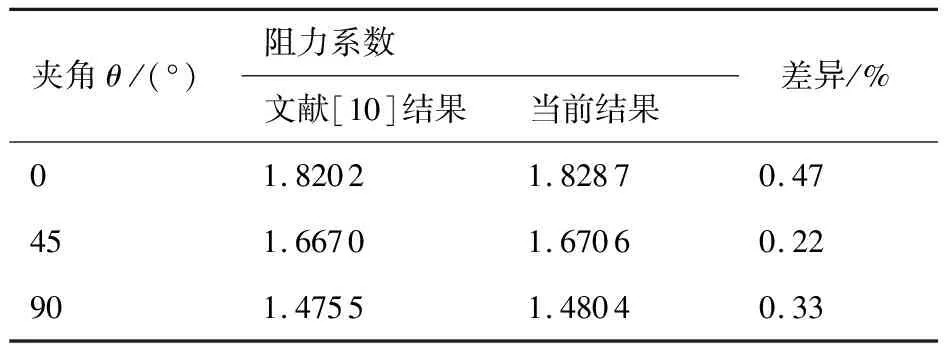
表1 球柱体阻力系数

5 数值计算分析

计算外形为：RAM-C钝锥体，头部半径为0.152 4 m，锥身半锥角为9°，全长1.295 m。计算条件为：高度71 km，速度7 650 m/s，壁面温度1 500 K。磁场仍采用配置于球心的偶极子磁场，B0=0.5 T，r0=0.152 4 m，方向为X轴负方向。

为了分析计算网格对数值模拟影响，图3给出两套网格数值计算的参数分布，Grid1为稀网格，物面法向间距2.5×10-6m；Grid2为密网格，物面法向间距10-6m，R为离开驻点的距离。可以看出，两套网格模拟结果几乎完全重合，这说明数值模拟受网格影响较小。为了保证流场有较高的分辨率，如无特殊说明，均采用密网格进行计算。

图3 不同网格条件下的电子数密度和表面热流

5.1 化学非平衡效应对磁流体控制影响

由气体模型的介绍可以看出，如果忽略热力学效应的影响，完全气体模型(PG)、平衡气体模型(EQ)和化学非平衡气体模型(CNEQ)恰好代表了化学反应 “冻结”“平衡”“非平衡”3种状态。由于真实的高温气体流场，整体来看化学反应是处于非平衡态(局部的冻结和平衡态可看作非平衡态的极限状态)的。因此，为了分析高温气体化学非平衡效应对高超声速磁流体控制效果的影响，本节采用这3种气体模型开展磁流体数值对比分析，得到化学反应非平衡效应对流场特性、气动力和气动热特性的影响规律。由于壁面催化作用相当于促使壁面附近气体趋向于平衡态，因此本文采用非平衡气体模型计算时，均采用完全非催化表面条件，以利于对比分析。

图4给出了无磁场条件下驻点线电导率、温度和电子数密度分布。由图可以看出，采用不同气体模型，计算结果差别非常大：采用完全气体模型，没有考虑化学反应的吸热效应，波后温度非常高，接近30 000 K，此时计算得到的电导率明显高于其他模型结果；采用平衡气体模型，化学反应达到平衡态，高温下气体离解较为充分和彻底，化学反应吸热效应达到最大，波后气体温度较低，气体电离程度(电子数密度)和电导率均较低；而采用化学非平衡气体模型，高温下气体存在一定程度的离解，但不够充分，化学吸热效应处于完全气体和平衡气体模型结果之间，因此电导率也介于这两者之间。本文完全气体模型和平衡气体模型的计算结果差异，与文献[7]的结果类似。

图4 不同气体模型驻点线参数(B0=0 T)

图5 不同气体模型驻点线温度的磁场作用

图6 不同气体模型的环形感应电流强度和洛伦兹力矢量

图5给出了有/无磁场条件下采用不同气体模型得到的驻点线温度分布。图6给出了采用不同气体模型计算得到的环形电流强度和洛伦兹力矢量分布。表2给出了采用不同气体模型计算得到的阻力系数及其磁场作用效率。可见，采用完全气体模型，磁场使激波脱体距离增加2～3倍，磁阻力伞较大，气体微元洛伦兹力矢量强度较低，阻力系数增加164%；采用平衡气体模型，磁场使激波脱体距离增加0.7～0.8倍，磁阻力伞较小，气体微元洛伦兹力矢量强度较大，阻力系数增加34%；采用化学非平衡气体模型，磁阻力伞和洛伦兹力处于完全气体模型和平衡模型结果之间，阻力系数增加67%。

这种现象可结合图4(a)进行分析：采用完全气体模型，波后电导率较高，同等条件下磁相互作用数较大，因此整体磁控效果较强，磁场使激波外推的距离较大，但由于波后相似的流动区域与磁偶极子中心的距离相对更远一些，结合方程(8)和方程(16)可知，其环形感应电流更小，因此洛伦兹力矢量强度相对较低；而采用平衡气体模型时，其结论恰好相反，采用化学非平衡气体模型，则处于上述两者之间。

结合图4～图6，可以看出，高温气体化学反应及其吸热效应，会显著降低波后气体温度，使电导率变小，在一定程度上削弱了磁阻力伞的整体效果，使磁控增阻效率下降；采用完全气体，忽略了这种化学反应效应影响，而采用平衡气体模拟，则在一定程度上放大了这种效应的影响。

图7给出了有/无磁场条件下采用不同气体模型计算得到的表面热流分布。表3给出了头部驻点、肩部(X=0.12 m)和锥身末端(X=1.14 m)处的热流及磁控热流变化幅度。可以看出，采用完全气体模型，磁场使头部区域热流明显下降，驻点下降50.3%，在肩部区域热流反而上升20.9%(这种热流“反冲”现象产生的原因见文献[22])，锥身大部分区域磁场作用效果不明显；采用平衡气体模型，磁场使热流下降的幅度较小，驻点热流下降28.9%，肩部热流上升36.5%，锥身大部分区域磁场作用效果不明显；采用化学非平衡气体模型，磁场使热流下降幅度较大，驻点热流下降47.3%，肩部热流下降32.3%，反冲现象不明显，锥身热流大幅下降，锥身末端热流下降63.3%。

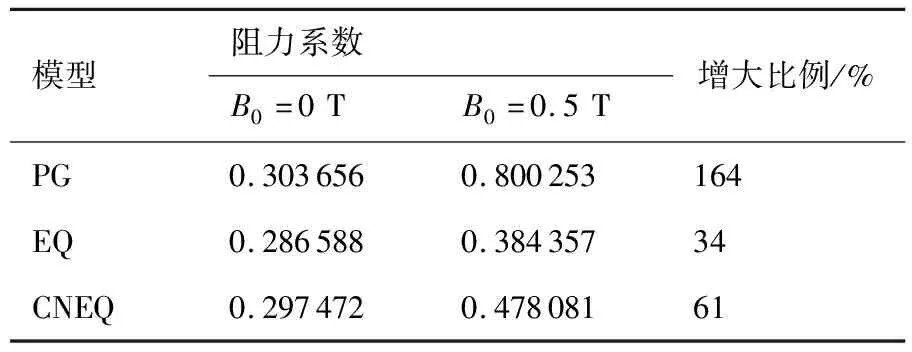
表2 采用不同气体模型的阻力系数

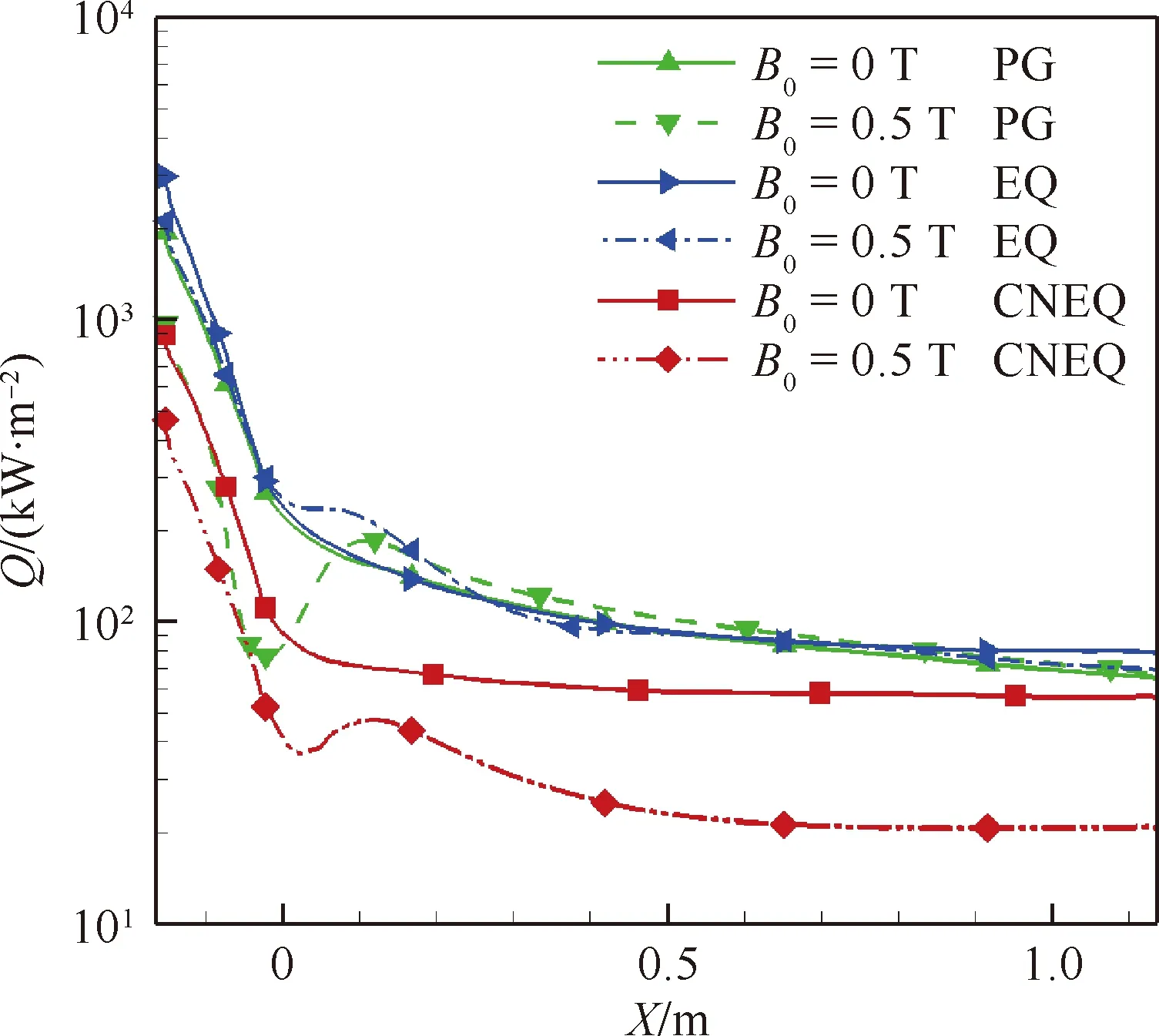
图7 不同气体模型条件下磁场对表面热流分布的影响

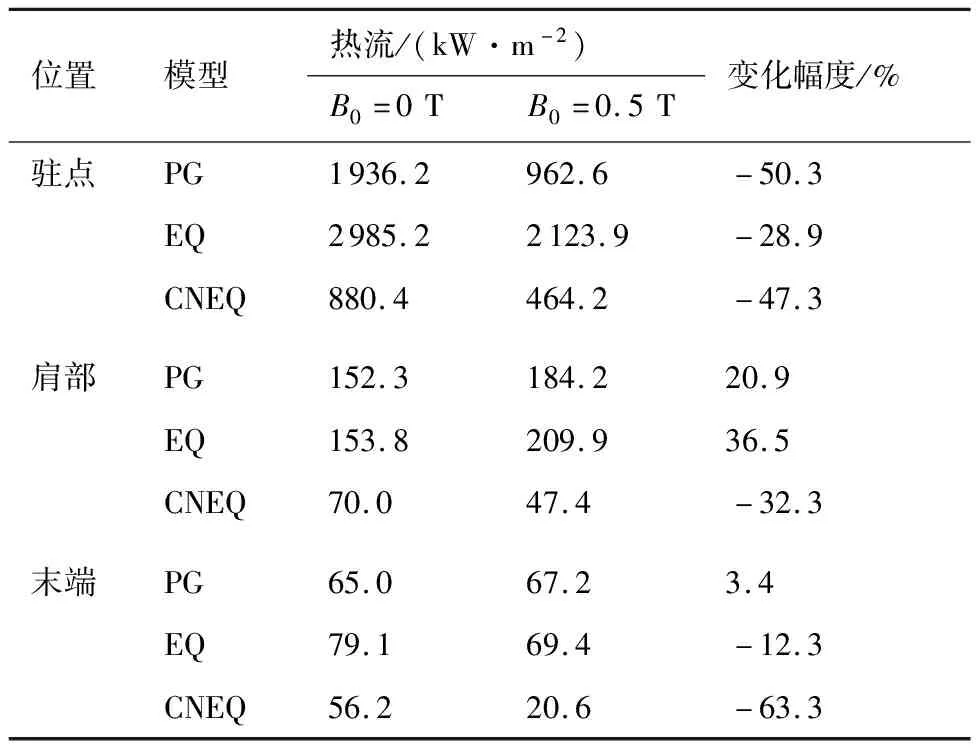
表3 不同气体模型得到的典型热流

由表3变化幅度对比可以看出，采用不同气体模型，锥身是磁控热流变化幅度差异最大的区域。为了进一步分析这种现象产生的原因，图8给出了锥身末端(X=1.14 m)处不同模型计算得到的温度、氮原子、氧原子分布，N为离开壁面的法向距离。可以看出，对于完全气体模型，化学反应“冻结”，磁场作用使激波脱体距离增加的同时，增大了壁面附近高温区气体温度，两者对热流的作用，在一定程度上相互抵消，因而热流变化不明显；对于平衡气体，化学反应达到平衡态，反应程度较为充分，在壁面温度1 500 K的平衡态条件下，壁面及近壁面区域，O、N等高生成焓组分将全部发生复合反应，其质量分数均为0，混合气体化学焓为基准值，其化学焓梯度也为0，此时热流主要是温度传导热流，磁场作用下其温度变化规律与完全气体模型结果类似，因此热流规律亦与完全气体类似；对于化学非平衡气体模型，化学反应处于非平衡态，壁面附近O、N等高生成焓组分来不及复合反应完全，其质量分数较大，气体化学焓相对较高，而磁场作用使O、N质量分数进一步增大，即磁场使壁面及近壁面区域的化学焓增大，化学焓的差异将导致气体温度分布的变化，近壁面温度梯度明显小于无磁场作用结果，热流因而显著下降。

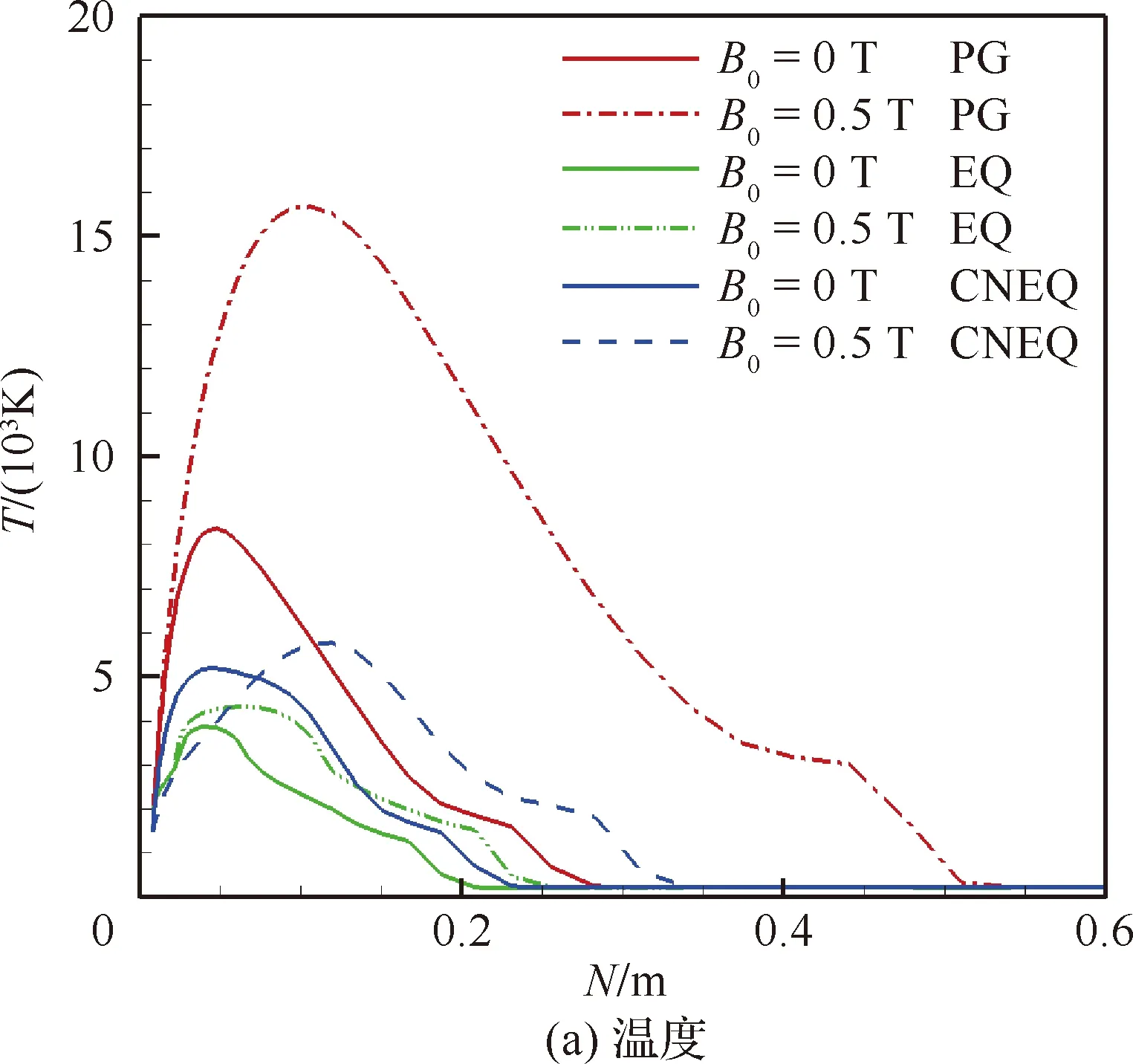
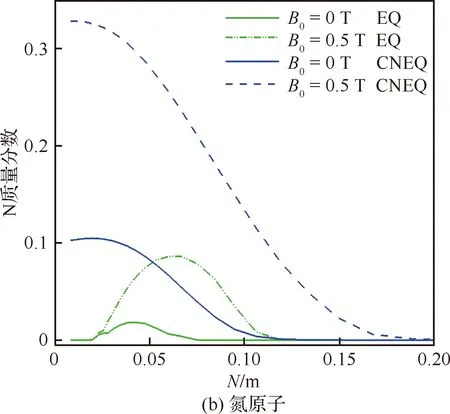
图8 不同气体模型条件下锥身末端参数分布

由此可见，高温气体化学非平衡效应对磁控降热效果的影响机制较为复杂，与流场中局部区域的化学反应“充分程度”(即非平衡特性)紧密相关；采用完全气体或平衡气体模型，均不能有效模拟这种局部的化学非平衡特性，其定性规律均存在较大的偏差，因此必须采用能模拟化学反应非平衡效应的气体模型。

5.2 热力学非平衡效应及焦耳热能量配比对磁流体控制影响

由气体模型的介绍还可以看出，化学非平衡气体模型(CNEQ)和热化学非平衡气体模型(TCNEQ)的主要差异在于热力学效应。为了分析热力学效应的影响，本节采用化学非平衡气体模型和热化学非平衡气体模型开展磁流体数值模拟，分析热力学温度激发-松弛过程的非平衡效应对流场特性、气动力和气动热特性的影响；为了分析焦耳热能量比对磁流体控制影响，在采用热化学非平衡气体模型时，考虑不同焦耳热振动能量配比γ=0～1.0，开展数值模拟研究。

图9给出了无磁场作用时驻点线电导率、温度、电子数密度分布。可以看出，两种气体模型，在无磁场时，激波脱体距离、温度与电子数密度分布规律类似，电离度和电导率差别较小，这说明，此时热力学非平衡效应对等离子体电学特性影响不大。

图10比较了两种非平衡气体模型磁场对温度和热流的影响(这里采用热化学非平衡气体模型时，γ=0)。表4给出了该条件下的阻力系数。可以看出这种条件下，两种非平衡气体模型，计算结果差异不大，磁场对激波脱体距离、表面热流分布、气动力特性的影响基本一致，这与图9“电学性质差异不大”的规律一致。这说明当γ=0时，热力学非平衡效应对磁流体控制效果影响不大。

图11给出了不同焦耳热振动能量配比条件下的表面热流分布和阻力系数变化。可以看出，磁场作用下，表面各区域热流受γ影响程度存在差别，头部区域受γ影响不明显，身部区域受γ影响相对复杂，但整体幅度变化不大；焦耳热振动能量配比对磁控增阻效应影响很大，主要影响洛伦兹力阻力分量(CD2)，随γ增大，洛伦兹力阻力分量迅速降低，磁场作用增阻效果D1由67%降到约12%。

图9 CNEQ和TCNEQ模型计算得到的驻点线参数分布

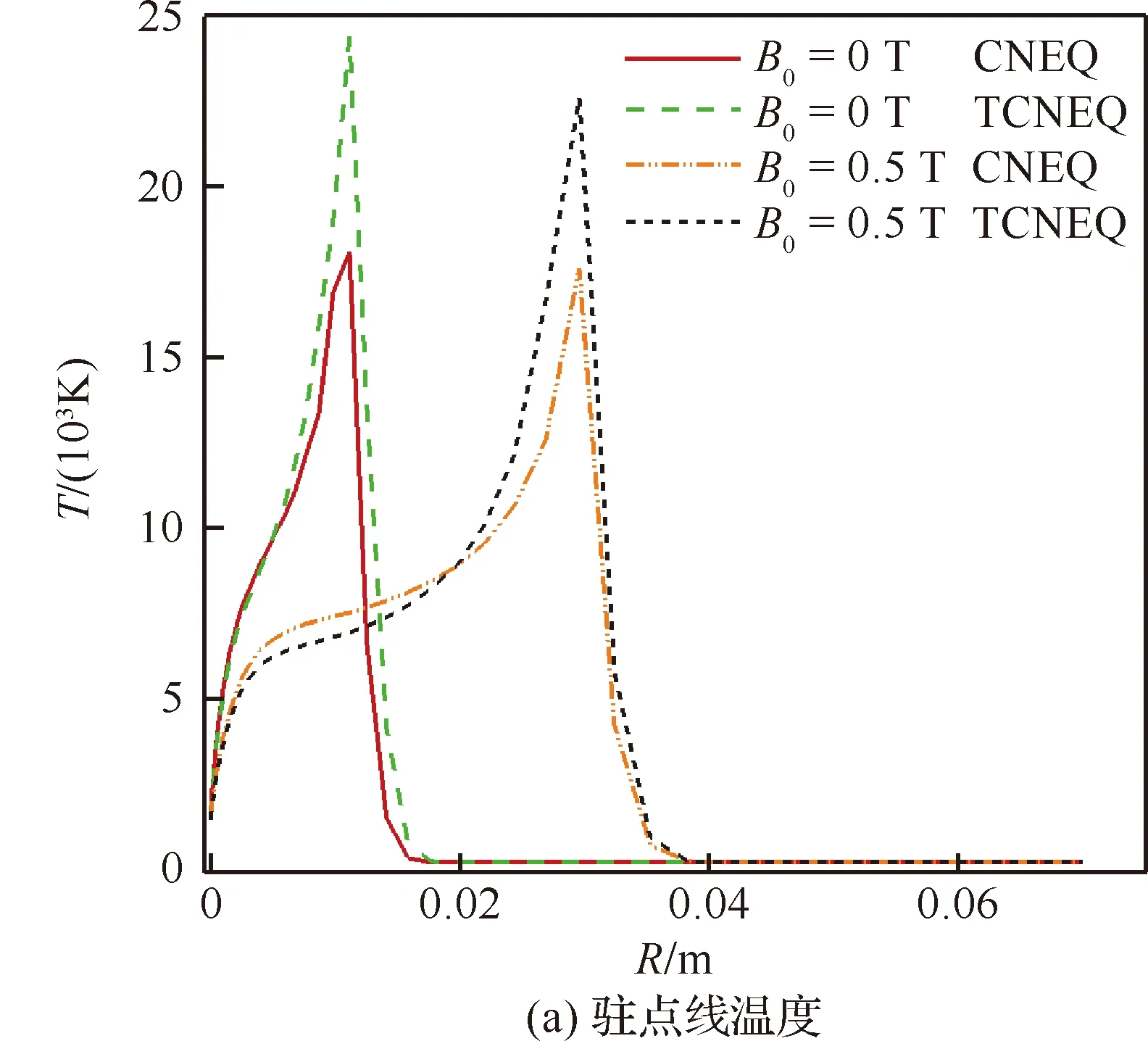
图10 CNEQ和TCNEQ模型磁场对温度和热流的影响

表4 采用CNEQ和TCNEQ模型得到的阻力系数

图11 不同焦耳能量比条件下磁场对热流和阻力系数的影响

为了分析这一现象的产生原因，图12给出了磁场作用下焦耳热振动能量配比γ=0.1(上)和γ=0.9(下)时流场中环形感应电流密度大小、振动-电子温度和平转动温度云图。可以看出，振动能量配比较大(γ=0.9)时，在流场中感应电流密度较大区域，振动温度由于焦耳热作用急剧上升，而平转动温度由于焦耳热能量分配较少，温度相对较低(图12(c)中标出区域对比)，此时，由温度引起的气体膨胀效应减弱，因此激波脱体距离减小，磁阻力伞较小，磁阻力系数下降明显。由于振动-电子温度沿流动向下游扩展，存在一定程度“近似冻结”现象，而热流受平转动温度和振动-电子温度传导共同作用，因此身部热流受γ影响相对明显。

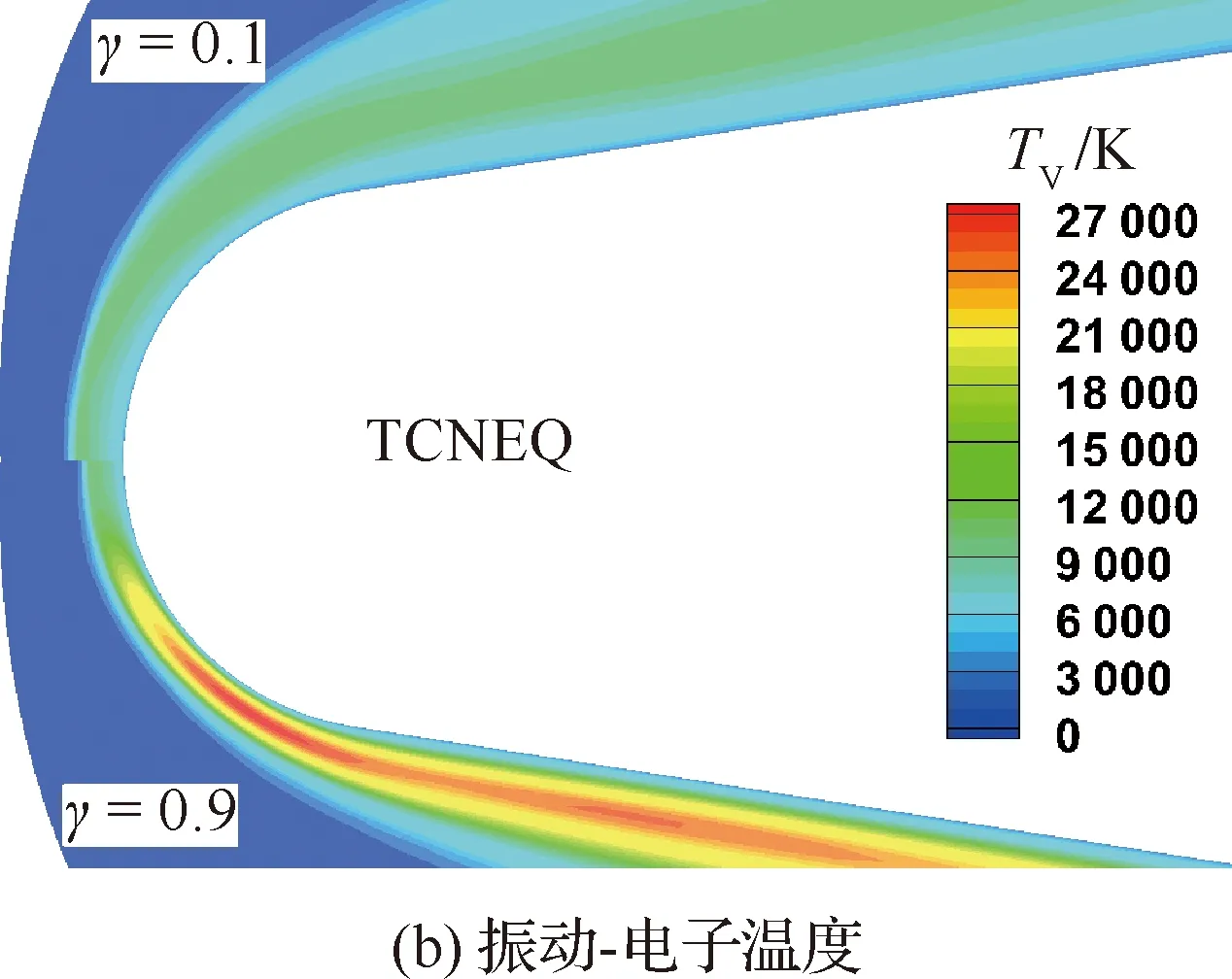
图12 不同焦耳热振动能量配比感应电流密度和温度云图

综合图10、图11、表4和图12可以看出，热力学非平衡效应对磁控效果的影响，与焦耳热能量配比紧密相关，当γ=0时，热力学非平衡效应影响效果不明显，随着γ增大，热力学非平衡效应影响效果逐渐显著，尤其是激波脱体距离和磁控增阻效果。

6 结 论

1) 化学非平衡效应对高超声速磁流体控制影响显著。在磁控增阻特性方面，化学非平气体模型模拟结果介于完全气体模型和平衡气体模型之间，完全气体模型结果偏大而平衡气体模型结果偏小；在磁控热流减缓特性方面，平衡气体和完全气体模型磁控热流变化的定性规律，与化学非平衡模型模拟结果差异很大，其产生原因与这两种模型不能较为真实地描述流场中化学反应非平衡状态有关。

2) 热力学非平衡效应对高超声速磁流体控制的影响，与焦耳热振动能量配比γ紧密相关。当γ=0时，磁场对气动力、热的作用效果，受热力学非平衡效应影响不大；随着γ增大，气动力系数的磁场作用效率有较大幅度的下降；磁控热流减缓效果受γ影响相对复杂，其中头部区域影响较小，身部区域相对明显。这与流场中振动-电子温度的“近似冻结”存在一定关系。

3) 高温气体效应会极大地降低磁控增阻效果，会明显地增强部分表面区域的磁控热流减缓效果。要准确数值模拟高超声速磁流体控制效果，必须有效考虑化学非平衡效应和热力学非平衡效应，采用热化学非平衡气体模型，同时选用接近实际情况的焦耳热振动能量配比。