“当”字型问题的解题逻辑
2020-03-24段雄东
段雄东


【摘要】“当”字型问题是初中数学常见的一类题型.由于其提问方式具有一定的特殊性,解题过程中容易出现两种逻辑错误:1.把“求证的结论”当作“已知条件”;2.把结论的必要条件当作充要条件.本文以两道题为例,通过对比错误的解法与正确的解法,分析出错的原因,并总结正确解法的表述方式.
【关键词】逻辑;分析过程;证明过程
在初中数学的学习过程中,我们经常会遇到这样的一类问题:当为何值时,可以得到给定的结论.我们姑且把这种形式的问题称为“当”字型问题.在解这类问题时,学生很容易出现以下两种不同的逻辑错误.
一、把“求证的结论”当作“已知条件”
学生在解“当”字型问题时,往往会搞不清楚题目中的已知到底是什么,要求或要证的又是什么.那么在解题过程中就会把“求证的结论”当作“已知条件”.下面我们一起来看一道例题.
例1 如图,在Rt△ABC中,∠C=90°,AC=BC=4 cm,动点P从点C出发以1 cm/s的速度沿CA匀速运动,同时动点Q从点A出发以2 cm/s的速度沿AB匀速运动,当点P到达点A时,点P,Q同时停止运动,设运动时间为t s.当t为何值时,点B在线段PQ的垂直平分线上?
显然这两个问题的“求证的结论”与“已知条件”是刚好颠倒的.问题1是:已知“点B在线段PQ的垂直平分线上”,要求“t的值”;问题2是:已知“t的值(这个值是多少也是我们去找)”,要证“点B在线段PQ的垂直平分线上”.
那么上面的解法一应该是对问题1的解答.解法二才是此题的正确解法.
可能有人会想:问题2是要通过“t的值”,证明“点B在线段PQ的垂直平分线上”.但“t的值”是多少,又是未知的,那不就相当于在未知的条件下去证明给出的结论.正因为如此,这类题目的解法,先要有一个分析的过程,得出“t的值”,然后在“t值”条件下再有一个证明过程,证明“点B在线段PQ的垂直平分线上”.
其实解法一与解法二的表述唯一的不同就在“∵点B在线段PQ的垂直平分线上,∴BQ=BP”与“当BQ=BP时,点B在线段PQ的垂直平分线上”.也正是这两句的不同才体现两种解法逻辑的不同.由于“点B在线段PQ的垂直平分线上”的充要条件是由“BQ=BP”一个条件构成的,我们才可以在解法二中把分析过程和证明过程合在一起,所以解法一与解法二的差别看起来并不是很大.
如果给定结论的充要条件是由两个或多个条件构成的,就能更好地体现分析过程和证明过程不同的作用.
二、把结论的“必要条件”当作“充要条件”
下面我们再来看例2的三种解法.
例2 两个全等的直角三角板ABC和DEF重叠在一起,其中∠A=60°,AC=4 cm.固定△ABC不动,将△DEF进行如下操作:
三种解法得出的结果都是一样的,当x=4时,四边形CDBF为菱形,但是只有解法三是规范的.解法一是针对问题“当四边形CDBF为菱形时,x为何值?”,出现了把“求证的结论”当作“已知条件”的逻辑错误.解法二和解法三,虽然都没有颠倒“求证的结论”与“已知条件”,但是解法三只有分析过程,与解法三相比,少了证明过程.
因为“条件CD=CF”是“四边形CDBF为菱形”的必要不充分条件,所以由“要使四边形CDBF为菱形,则必须CD=CF”分析得到必要条件“CD=CF”,从而得出x=4.那也就是说当x=4时,只有必要条件“CD=CF”成立,在此条件下,四边形CDBF只是有可能为菱形.所以说解法二只有分析过程,分析x=4是怎么得出来的,并不能确定四边形CDBF一定为菱形.
要判定四边形CDBF为菱形,后面还必须要有证明过程.例如解法三,通过x=4这个条件,得出DB=CF,再结合DB∥CF,得到四边形CDBF为平行四边形,这样才得到“四边形CDBF为菱形”的充要条件“CD=CF,四边形CDBF为平行四边形”,那么根据菱形的概念“有一组邻边相等的平行四边形是菱形”,我们才可以证明四边形CDBF为菱形.
“四边形CDBF为菱形”的充要条件是由两个条件“条件①:CD=CF”和“条件②:四边形CDBF为平行四边形”构成的,解法二错把必要条件“条件①:CD=CF”当成了充要条件.虽然得出的结果都是x=4,但是作为解答题,解法二是不完整的,是不规范的.如果没有理解这里错误的原因,那么学生在以后的学习中还会犯同样的错误.
就像曹建全老师说的,“解题过程实际上是一个不断转化的过程.”在转化过程中,一般都要求进行等价转化,即不断寻求已知条件的充要条件,这样才能使所求得的解不至于扩大或缩小.
三、中考中的“当”字型问题
“当”字型问题的题目还是比较多的,也是中考中的“常客”,像例3,它是2019年广东省中考数学卷的压轴题,其中的第(3)问也是“当”字型问题.
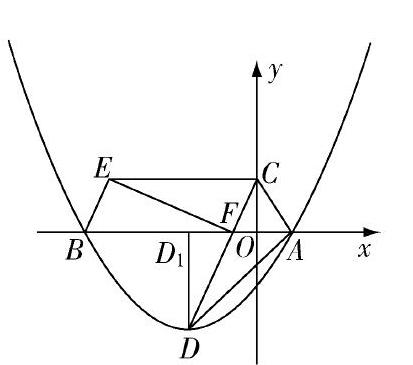
例3 如图,在平面直角坐标系中,抛物线y=38x2+334x-738与x轴交于点A,B(点A在点B的右侧),点D为抛物线的顶点,点C在y轴的正半轴上,CD交x轴于点F,△CAD绕点C顺时针旋转得到△CFE,点A恰好旋转到点F,连接BE.
(1)求点A,B,D的坐标;
(2)求证:四边形BFCE是平行四边形;
(3)过顶点D作DD1⊥x轴于点D1,点P是抛物线上一动点,过点P作PM⊥x轴,点M为垂足,使得△PAM与△D D1A相似(不含全等).
①求出一個满足以上条件的点P的横坐标;
②直接回答这样的点P共有几个?
分析 第(3)问虽然没有出现“当”字,但是跟“当”字型问题一样,我们可以把此问理解为“当点P的横坐标是多少时,△PAM与△DD1A相似(不含全等)”.这题的逻辑还是比较简单的.在∠DD1A=∠PMA=90°的条件下,要使得△PAM与△DD1A相似,只要补充两角对应夹边的比相等就行,又因为对应关系的不确定,所以要用分类思想.也就是说虽然△PAM与△DD1A相似的充要条件是两个条件组成的,但是有一个是已知的,所以解题过程中只要说明另一个就行,我们也就可以把分析过程和证明合二为一.如下:
四、总结
数学解题最核心的逻辑是:已知是什么、求解或求证的是什么.像这种的“当”字型问题的解题过程中经常把“求证的结论”当作“已知条件”,或者把结论的必要条件当作充要条件,究其原因主要有两个:一是已知条件中的数值也是未知的,需要我们通过分析才能得到;二是得到了已知条件中的数值,还要进行证明,得到结论的充要条件.
要做好“当”字型问题的题型,关键是要学会怎样表述解题过程,总结如下:“当”字型问题的解法概括起来分两种情况.一、若给定结论的充要条件只有一个时,则分析过程和证明过程就可以用形如“当在这个条件(直接写)时,有给定的结论”的逻辑语合二为一,然后再通过这个条件推算出我们要的值,如例1解法二;二、若给定结论的充要条件是由两个或多个条件构成时,则分析过程和证明过程就一定要分开.分析过程就用形如“要有给定的结论,则必须有条件①”的逻辑语,在这个条件下推算出我们要的数值,再在这个数值的条件下去证明条件②等剩下的其他条件也成立(证明过程),从而说明了“当在这个数值时,有给定的结论”,如例2解法三.
数学是一门具有严密逻辑系统的科学.要想学好数学必须具备三大能力,即运算能力、空间想象能力和逻辑思维能力,其中逻辑思维能力是核心,因此,培养学生的逻辑思维能力就成为数学教学的重要目的之一.如果我们解题时只重视最后的答案而轻视解题过程的逻辑,就失掉了教学的本意.
【参考文献】
[1] 王岩.数学解题中的逻辑思想[J].数学学习与研究:教研版, 2012(19):93.
[2] 曹建全.运用必要条件解题致错例析[J].中学数学月刊, 2005(5):43-45.
[3]曹建全.数学解题中的常见逻辑失误例析[J].上海中学数学,2006(6):27-29.
