测大角归化法归化值的两种计算方法及其精度分析

彭维 杜升 邓雨弦

摘要：测大角归化法直线放样是根据已知点坐标与放样点坐标，反算出放样元素，放样出近似点。然后以近似点为测站，测定两个控制点与近似点的夹角，再通过数学手段计算出归化值，然后根据归化值将近似点位置归化到设计点位置的从而达到精确放样直线的目的方法。由于其操作简单常被用施工建设中，所以本文对测大角归化法归化值的两种计算方法的精度进行一定的分析研究。

关键词：测大角归化法;精度分析

测大角归化法是在根据已知数据反算放样数据，然后直接放样，得到过渡点平面位置。然后测量两已知点与过渡点的夹角，再通过数学手段求得过渡点位置与设计点位置的偏差，然后根据偏差将过渡点归化至设计点。采用此方法可以降低由仪器误差带来的对放样精度产生的影响。由于采用的计算归化值的方法不同，所以需要对两种计算方法的精度进行分析研究，以确定在同等观测条件下谁的精度更高。

1 测大角归化法原理

1.1 测大角归化法三角函数计算归化值法原理

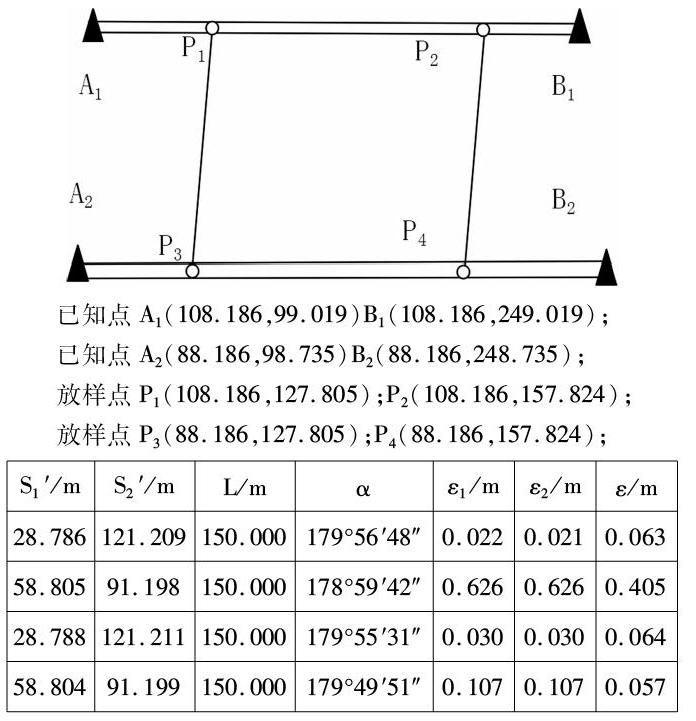
已知点A，B，P的坐标，为放样出直线AP，首先应该根据首先应根据P点的设计坐标及已知点A点与B点的坐标反算出AP边长S1与BP边长S2，再根据放样元素放样出点P′，然后以P′为测站，于A、B两点处架设棱镜，测量∠AP′B及AP，BP的长度S1′、S2′，在归化图纸上绘制点P′，再过点P′绘制夹角∠AP′B为的两条直线，并过在直线上截取长为S1的线段P′A与长为S2的线段P′B，然后连接AB，再在AB截取长为S1的线段AP，P点即为设计点位置[1]，最后通过数学手段求出归化值PP′。

1.2 测大角归化法三角形面积计算归化值法原理

已知点A，B，P的坐标，为放样出直线AP，首先应该根据首先应根据P点的设计坐标及已知点A点与B点的坐标反算出AP边长S1与BP边长S2及AB长度L，再根据放样元素放样出点P′，然后以点P′为测站上，于A、B两点架设棱镜，测量∠AP′B及AP，BP的长度S1′、S2′，再在归化图纸上绘制过渡点P′，过点P′绘制夹角∠AP′B為的两条直线，并在直线上截取长为S1，S2的线段P′A，P′B，然后连接AB，在直线AB截取长度为S1的线段AP，P点即为设计点位置[2]，最后通过数学手段求出归化值PP′。

2 精度分析

2.1 归化值通式

通过数学手段可以求得两种计算方法的归化值通式

设Δα=180°α

三角函数法归化值通式：ε=PP′=S′1*S′2S′1+S′2*Δαρ

三角形面积法归化值通式：ε=PP′=S′1*S′2L*Δαρ

2.2 精度分析

由以上测的不同的几组数据比较分析可得出：同等观测条件下在误差允许范围内两种方法精度相同。

3 结论

在工程的施工建设中，测量的主要工作是施工放样且精度要求较高，本文对测大角归化法放样直线归化值计算方法进行了探讨，在经过对数据精度比较分析后发现在同等观测条件下三角函数法计算归化值与三角形面积法计算归化值精度相同，所以在采用测大角归化法直线放样时，选择计算可以直接选用计算更简单的三角函数法归化值通式。

参考文献：

[1]周保兴，朱爱民.工程测量学[M].北京：人民交通出版社，2018.2.

[2]张正禄.工程测量学[M].武汉：武汉大学出版社，2013（2版）.

作者简介：彭维（1998），女，汉族，四川遂宁市人，土木环境与工程系，研究方向：地理信息遥感，工程测量。