基于自适应随机共振的轴承故障诊断研究

许自立 乔印虎 李 进 王 浩 张春雨 鲍官培

(1.安徽科技学院 机械工程学院,安徽 蚌埠 233100;2.青岛理工大学(临沂)机电工程系,山东 临沂 276000)

0 引言

随着电力驱动技术发展，电机的开发和应用不断延伸，其运行环境复杂多样且变化具有不可预测性，电机设备诊断参数和故障特征常受环境影响导致信号微弱混乱，难以提取与分析.统计显示，电机约70%的机械损坏是由轴承各种故障引起的.作为诊断高速旋转轴承部件缺陷和早期故障的最佳方法之一，振动分析中的振动特征信号的提取和处理的不断优化能够有效解决电机轴承的故障诊断问题[1-2].

基于信号处理技术的振动分析在旋转机械故障诊断中应用广泛且方法多样，但传统方法难以检测和提取低信噪比环境的早期微弱故障特征，且在消除噪声处理时一定程度上会损坏故障特征信号.利用随机共振[3]处理方法使系统中的微弱特征获得噪声能量，其和周期性信号具有协同作用以实现自身的增益和提取[4-5]，可以有效对电机轴承早期故障诊断提供支持.潘峥嵘等[6]利用经典双稳态随机共振，研究了电动机轴承微弱故障特征信号的增益和提取；段佳雷等[7]提出非饱和随机共振的方法研究了轴承的早期故障诊断；许自立等[8]提出了基于最大相关谱峭度解卷积的轴承早期故障诊断方法；Zhou等[9]利用混合指标用于衡量逻辑随机共振系统的响应，研究了滚动轴承等旋转机械的故障诊断.Murali等[10]在研究的非对称施密特触发器中验证了逻辑随机共振并为非对称共振处理提供了支持.Gerashchenko[11]研究了周期信号及高斯白噪声环境中的非对称随机共振行为，阐释了不同噪声强度对随机共振的诱导效果.结果显示一定条件下非对称随机共振处理的效果相较于对称随机共振更好.

该电机轴承故障诊断研究方法基于非对称势函数，推导得到对应的过阻尼系统的输出表达，提出自适应非对称阱宽随机共振的方法，实现对滚动轴承早期轻微故障的诊断.仿真和试验结果显示，提出的方法效果优于集成经验模式分解法，能够有效地实现轴承故障特征的增益和提取并据此进行故障分析判断.

1 非对称阱宽随机共振系统输出

在非线性系统中，受内外噪声和周期外力一起形成协同作用导致输出响应增强，布朗粒子在经典过阻尼双稳态势阱中的跃迁可通过爱因斯坦关系表示为[12]：

(1)

式中A、Ω与η(t)分别为信号幅值、角频率与高斯白噪声.

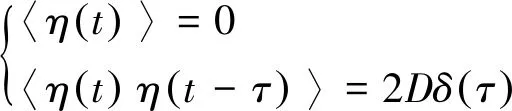
(2)

式中D与U(x)分别为噪声强度与具有非对称性的阱宽势函数：

(3)

式中a，b是系统参数；α为非对称因子，且所有参数均大于0.

图1 非对称阱宽势函数

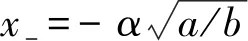
(4)

一方面，在存在周期力的情况下势函数U(x)被周期力所调制，因此势函数具有以时间为自变量的周期性.假设周期外力的幅值足够小(A≪1)，则在无噪声的情况下被激励粒子仍不足以在两个势阱之间来回跃迁.另一方面，假设周期外力的变化足够缓慢(Ω≪1)，则系统在1/Ω周期内足够达到局部平衡状态[14].那么对应于等式(4)的概率密度函数表达式为：

(5)

其中，N为归一化常数，且广义势函数为：

(6)

根据两态理论，等式(1)中的双稳态系统能够简化为n±(t)的两态系统[15]，描述n+(t)的主方程为：

W+(t)n+(t)

(7)

式中，W±(t)是稳态x±的跃迁概率，且在小参数条件下利用泰勒级数可以描述为：

W+(t)=μ1-β1Acos(Ωt)+o(A)

(8)

W-(t)=μ2+β2Acos(Ωt)+o(A)

(9)

对式(7)进行积分处理且计算自相关函数[16]，得到系统输出信噪比的解析表达式为：

(10)

式中μ1=W+(t)

(11)

(12)

根据平均首次穿越时间，即克莱姆逃逸速率，得到W±(t)的表达式如下

W±(t)=

(13)

等式(13)被计算得到

W+(t)=

(14)

W-(t)=

(15)

由等式(10)式(11)和式(12)可以推导得到自适应非对称性阱宽随机共振系统的信噪比表达式

(16)

利用式(16)分析非对称阱宽随机共振，由图2表明随着噪声强度D及参数a与b不断变化，信噪比呈现单峰结构，显示随机共振现象发生在非对称阱宽随机共振系统中，而且随着非对称因子α的增加，该系统输出的最大信噪比也随之增强，说明非对称阱宽能够改善随机共振的增益性能.

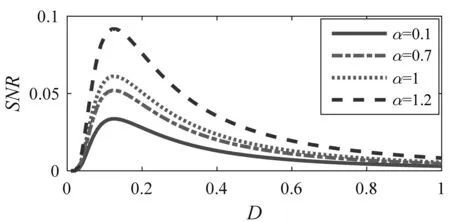
(a)不同非对称因子下信噪比随噪声强度D的变化

(b)不同非对称因子下信噪比随参数a的变化

(c)不同非对称因子下信噪比随参数b的变化

图2非对称阱宽输出信噪比变化

2 非对称阱宽随机共振的轴承故障诊断方法

根据上述研究，提出一种轴承早期轻微故障诊断方法，具体步骤如下.

2.1 信号处理

应用希尔伯特解调技术释放被调制的故障特征频率信号，获得随机过程的振幅随时间变化的包络信号曲线.随后采用频移尺度变换方法处理该随机过程，使其满足随机共振参数调节输入条件[17].

2.2 目标函数

将前面经过频移尺度变换压缩方法预处理得到的包络信号代入非对称阱宽随机共振系统，预设置频移尺度变换的参数，利用四阶龙格-库塔法解出等式(1)中爱因斯坦关系式[18]，获得系统的输出响应，通过式(17)得到系统的输出信噪比，将其作为量子遗传算法的自适应度函数.

(17)

其中Ad表示系统的输出信噪比幅值，Ai表示每个信号幅值，N表示变换以后包络的长度[19].

2.3 优化更新

初始化系统参数的搜索范围为a∈(0,10]，b∈(0,10]和α∈(0,10]，并初始化量子遗传算法参数，其最大遗传代数20，种群规模40[7].根据搜索的每个节点的信噪比浓度变化优化系统参数和非对称因子，记录最佳输出信噪比SNRbest以及对应的最优参数对(a,b,α)best.

2.4 故障特征频率提取

利用最优参数对(a,b,α)best调制非对称阱宽随机共振系统，得到轴承故障特征频率处的最佳随机共振系统，并将移频尺度变换预处理得到的包络作为该最佳随机共振系统的输入信号，利用四阶龙格-库塔法求解该非对称阱宽随机共振系统的响应信号.然后对该响应信号进行傅里叶变换提取得到轴承故障特征频率[20]，根据具体轴承参数计算其理论值并加以对比，最终实现轴承的故障诊断.

3 仿真分析

模拟一个单调指数递减信号，其冲击幅值取1，采样频率取10 kHz，采样时间取1 s，轴承外圈故障特征频率设65 Hz.由于电机实际运行环境复杂多样，采集到的故障信号一般包含噪声干扰信号，图3(a)表示冲击特征和混合信号的时域波形，可以看出外圈故障的冲击特征被噪声信号掩盖，难以有效分析；图3(b)表示该系统混合信号的频谱，判断在1 000 Hz频谱处明显存在一定的共振频带；图3(c)表示该系统混合信号的包络谱，但从中无法判断出65 Hz的故障特征频率.以上信息无法判断电机轴承是否发生故障，若判断为不存在故障，会导致安全隐患及事故风险.

(a)混合信号

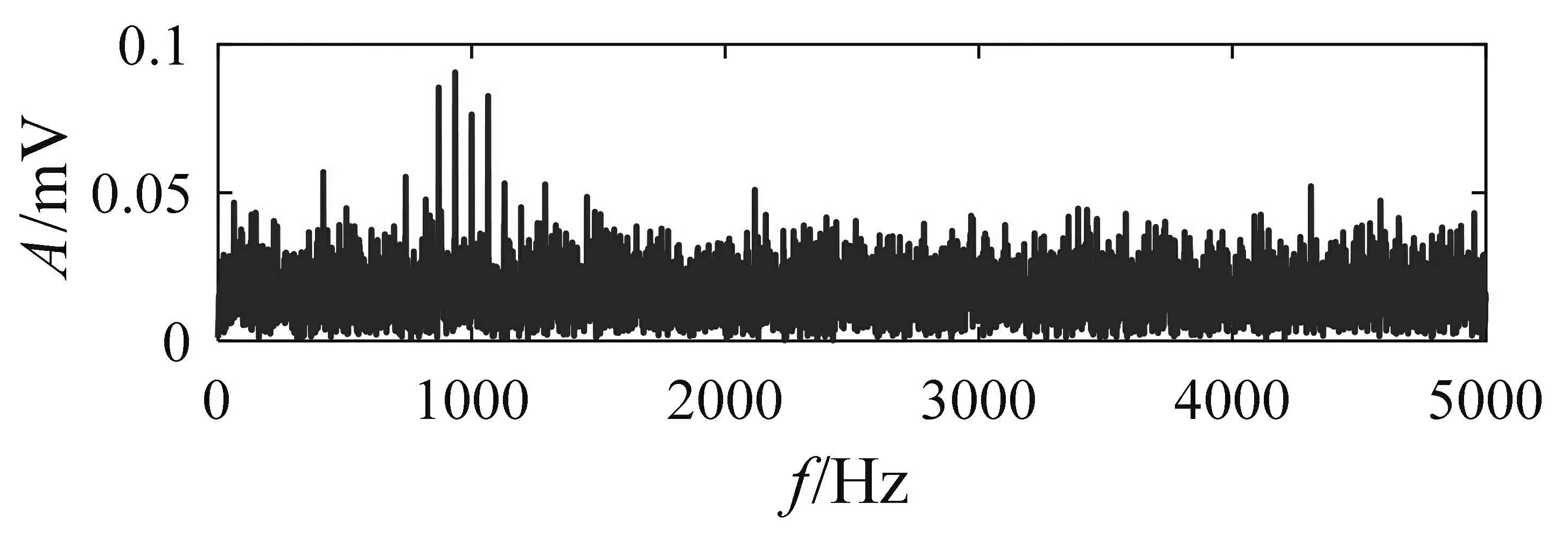
(b)频谱

(c)包络谱

图3轴承待检信号

所以，利用提出的非对称阱宽随机共振方法处理图3(a)所示的混合信号，采用频移尺度变换以压缩故障频率信号使其满足随机共振的输入条件.由于随机共振系统等效于一个低通滤波器，难以消除低频噪声，因此需要利用高通滤波器尽量消除低频干扰.此外，受绝热逼近理论的限制，随机共振只能检测频率小于1 Hz的信号，所以需要利用频移尺度变换平移和压缩待检故障特征频率，在这里高通滤波器的通带截止频率设置为56 Hz，阻带截止频率设置为60 Hz，尺度变换的频移为56 Hz，尺度因子为200[7-8].那么得到平移压缩后的故障信号特征频率为(65-56)/200= 0.045 Hz远小于1 Hz，满足本系统随机共振待检信号输入条件.图4为利用研究提出的方法所检测结果，从图4(b)可以看出在整个频谱中故障特征频率65 Hz处非常明显，而且时域特征具有明显的周期特性，表明轴承外圈可能发生故障，这一结论与模拟故障实际位置一致，说明提出的方法可以有效地增益和提取轴承故障征兆信号，能够实现轴承的早期故障诊断.

(a)时域波形

(b)频谱

图4非对称阱宽随机共振检测结果

集总经验模式分解，简称EEMD，经常用于增益和提取轴承故障征兆特征，其前五个内禀模态分量(IMF1-IMF5)的包络谱见图5[21].显然，从图5中很难观察到轴承外圈故障特征频率65 Hz，依据EEMD方法的结果很难判断轴承是否发生故障，原因是EEMD方法是通过消噪处理进行特征提取，处理时易导致信号特征缺失，随机共振则采用对噪声进行能量增益以便提取故障特征频率，上述仿真试验说明提出的非对称阱宽随机共振方法具有较好的可行性和有效性.

4 试验验证

采用Case Western Reserve University公开轴承试验数据[2]验证非对称阱宽随机共振轴承故障特征提取方法.通过一个1.47 kW电机驱动，采样频率取48 kHz，采样时间取2 s，轴承转速取1 750 rpm，样品类型为电机驱动端深沟球轴承，该轴承的外圈部位故障大小选择0.007英寸，外圈故障的理论特征频率是104.56 Hz.在高斯白噪声条件下的时域波形及频谱如图6，高斯白噪强度为7.从图6(c)包络谱图中发现在105 Hz处有微弱的轴承外圈故障特征频率信号，与理论差值为0.443 Hz，据此判断105 Hz是实际轴承外圈故障特征频率，鉴于附近的干扰噪声较多，无法准确判定有无早期故障的发生.

图5 EEMD检测结果

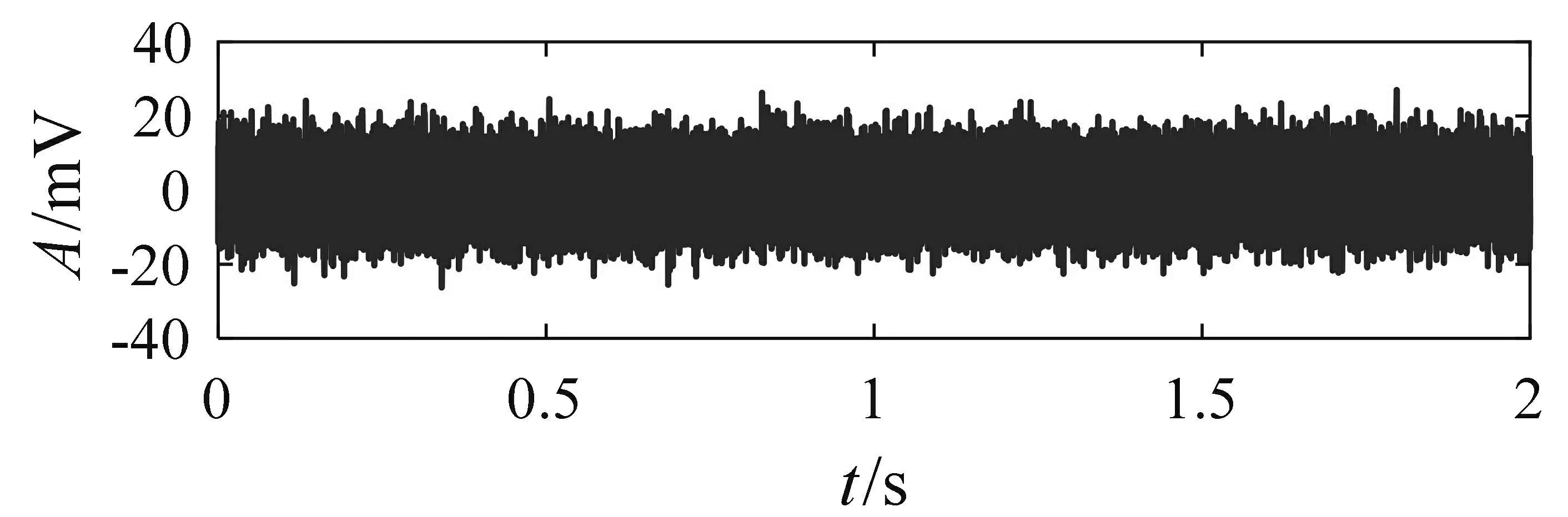
(a)时域波形

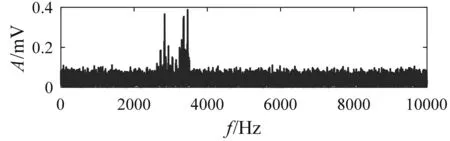
(b)频谱

(c)包络谱

图6外圈故障信号

利用非对称阱宽随机共振方法处理图6(a)所示含噪声信息的轴承故障信号，输出信号的时域波形及频谱如图7(a)及7(b)所示.轴承外圈故障特征频率在105 Hz处有比较明显的增强性共振，且其在整个频谱中占主导地位，可以据此判断轴承发生了早期故障.同样，利用EEMD方法处理图6(a)的轴承外圈故障信号，前五个IMF的包络谱如图8所示.从IMF1的包络谱中可以看出轴承外圈故障特征频率以及倍频信息，但其幅值微弱，难以判定故障的发生.通过非对称阱宽随机共振方法能够将噪声的能量转化为故障特征能量，不仅削弱了噪声而且增益了故障特征，展现出更好的增益能力.结果轴承外圈故障试验同样证明了非对称阱宽随机共振的有效性.

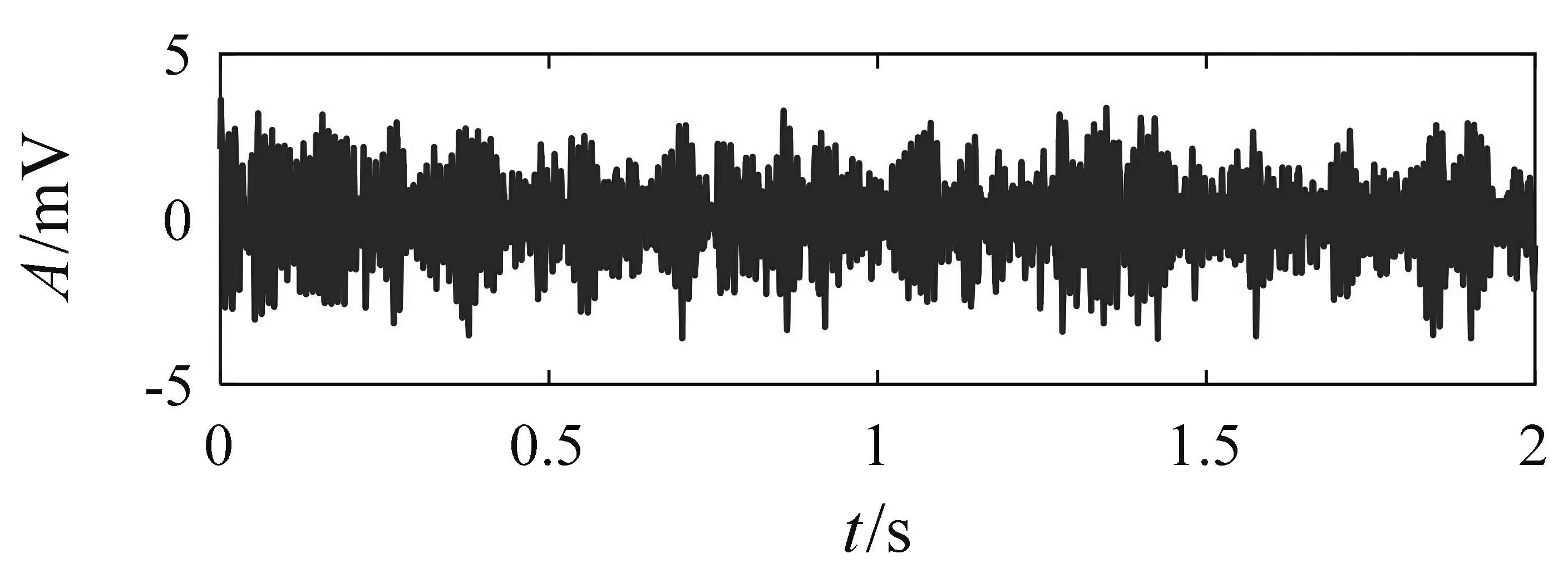
(a)时域波形

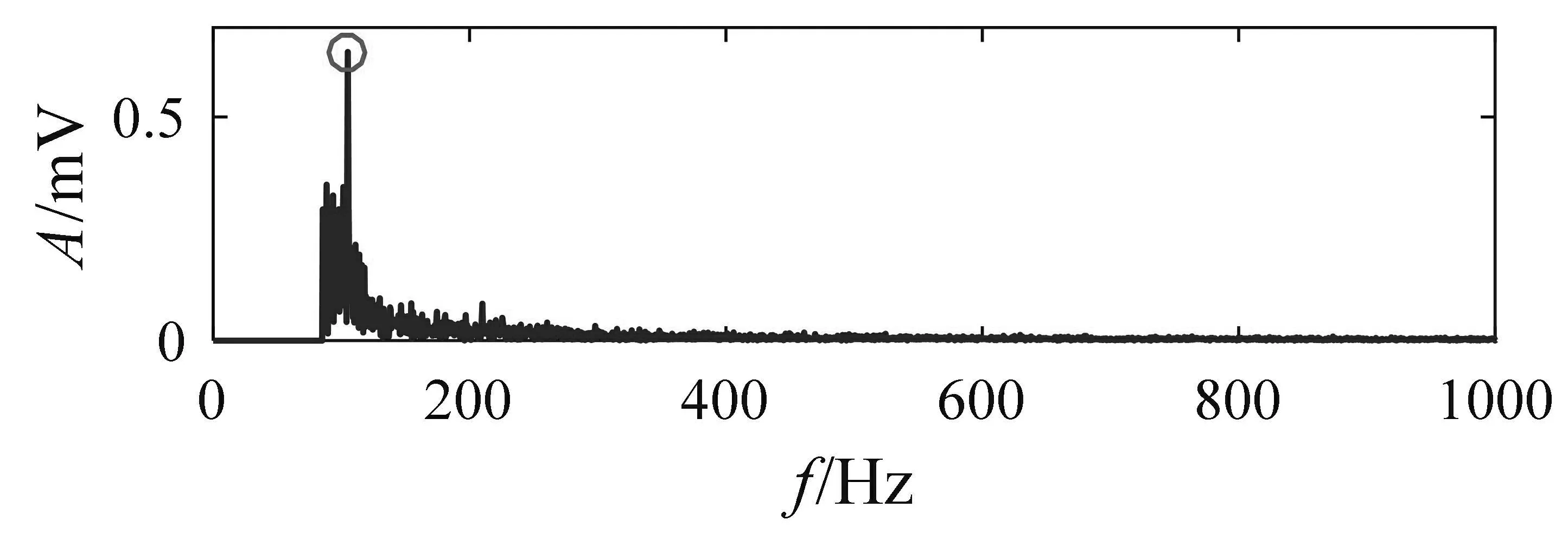
(b)频谱

图7非对称阱宽随机共振增益提取结果

为了进一步验证方法的可行性，把一个内圈带有尺寸为0.007英寸缺陷的滚动轴承安装到试验台上，转速设置在1 750 rpm正常运行时采集轴承振动信号，其时域和频谱如图9.可以看出轴承故障特征频率157.94 Hz处信号被环境噪声所淹没，很难判定是否发生故障.利用EEMD方法处理结果如图10，虽然在内禀模态分量IMF1的包络谱中能够看到微弱的故障特征频率信号，但是整个频带分布大量噪声干扰频率，很难判定频带中的峰值一定是故障特征频率，而不是噪声的干扰.同时，利用非对称阱宽随机共振方法对轴承内圈故障振动信号处理，结果如图11，可以看出轴承内圈故障特征频率处有明显峰值，而且该频率幅值在整个频谱中占据主导地位，由此能够判定轴承内圈发生了局部故障.对比结果可以看出，提出的方法具有较好的故障信号增益和提取能力，优于EEMD方法，由于非对称阱宽随机共振方法能够利用信号本身的噪声增益故障特征，且对系统的有效控制使得随机共振具有更强的增益能力.

图8 EEMD检测结果

(a)时域波形

(b)频谱

图9轴承内圈故障信号

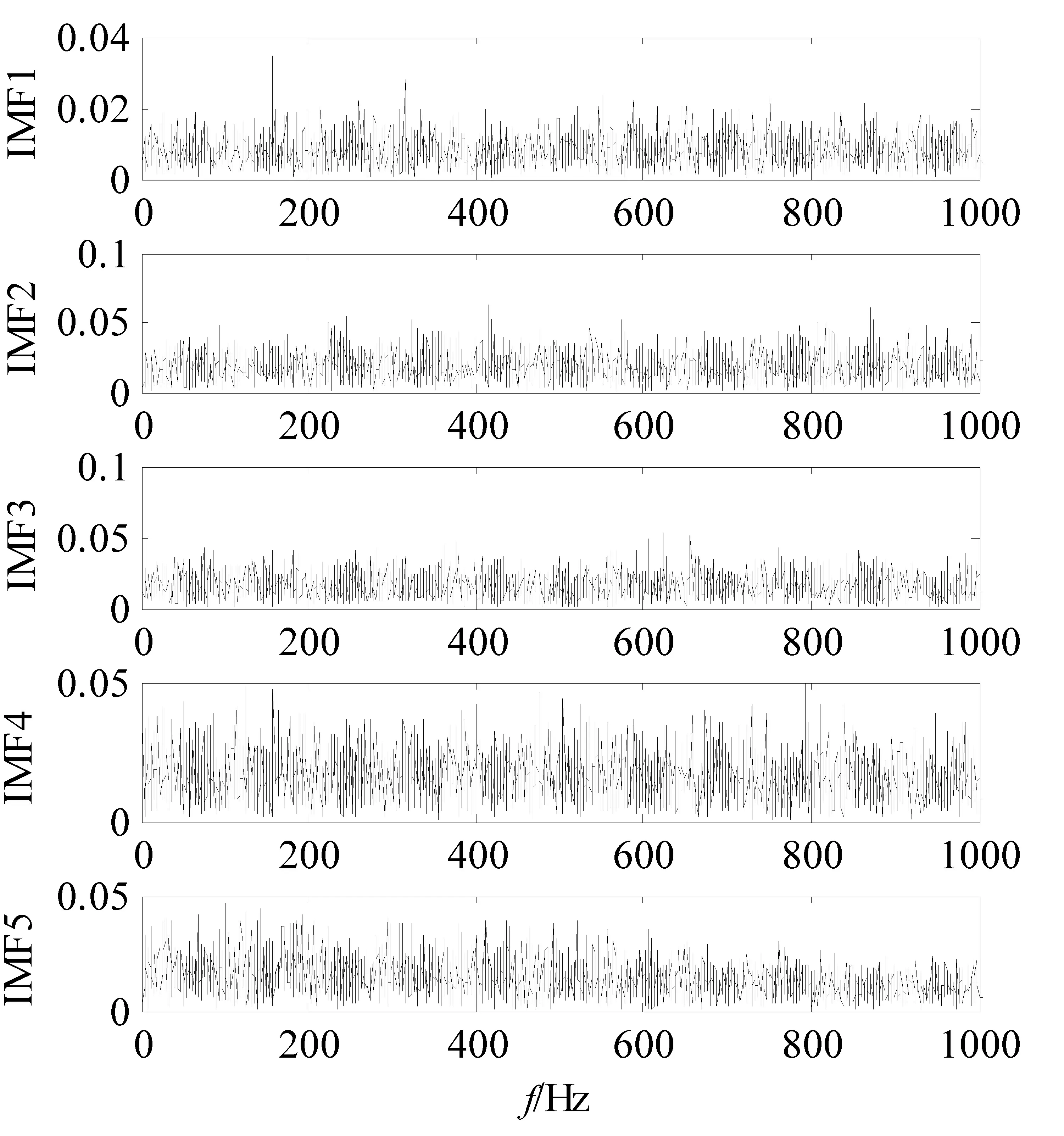
图10 EEMD检测结果

(a)时域波形

(b)频谱

图11非对称阱宽随机共振增益提取结果

5 结论

针对通过电机轴承的振动信号进行早期故障诊断，提出的非对称阱宽随机共振方法能够利用噪声增益很好提取故障特征，且阱宽变化可以对随机共振实现更精细的控制，该方法相比于EEMD法展现出更好的增益结果.仿真和轴承故障试验表明，非对称阱宽随机共振比EEMD具有更好的增益和提取能力，证明了该方法的有效性.需要指出的是，该方法仅能定性判断故障是否存在，难以定量检测轴承故障的发展程度，且未考虑电机瞬时过载的影响，具有一定的局限性，对于移动端如电动汽车上的电机轴承检测效果尚未评价.后续研究的重点是基于随机共振的电动汽车电机轴承持续监测与诊断.