数据驱动下定子绕组出水温度在不同工况下标准值的确定

李鹏竹

（宁夏京能宁东发电有限责任公司，宁夏 银川750001）

1 概述

对于大型火力发电厂来说，在保证设备安全经济稳定运行的前提下，追求更高的经济效益，节约检修成本支出，对设备的检修采用“点检定修”显得尤为重要，点检定修必须精准检修，所以要确定每一个设备的劣化程度，对该设备进行检修，对于发电机来说实现状态的检修必须对故障特征参数做到精准的预测，我国汽轮发电机运行规程中规定的线棒允许限制，一方面只是从绝缘材料和冷却系统所承受的最高温度，并不是发电机运行的实际温度，实际温度与发电机冷却介质的进水、进氢温度和发电机的设计温升有关，更不是状态监测及故障诊断中所需要的标准值。另一方面由于各线圈在制造工艺上的差异、附加损耗的不同，是否有引线等，在同一工况下，各测点的温度不尽相同，甚至差异较大，从现场获得的数据可以证明这一点，所以，对各测点制定状态监测所需要的温度标准值显得尤为重要。

从20 世纪80 年代开始，许多专家对定子线棒温度进行了预测，阅读大量文献，确定温度模型有六种方法，五种方法是运用五个经验的温度模型进行预测。分别是：李永刚老师定子绕组温度模型，蒲莹老师定子绕组温度模型，指纹系数判断法温度模型，数值计算法温度模型，许伯强老师温度模型，第六方法是采用人工神经网络方法。文献1 采用曲线拟合和蒲莹经验公式和神经网络两个方法进行预测，并对两种结果进行了比较。

本文在上述文献1 的基础上，根据现场实际运行经验，利用指纹系数判断法运用最小二乘法拟合指纹系数确定温度预测模型和BP 神经网络预测不同工况下温度标准值进行进一步的研究。结果表明，运用指纹系数判断法和神经网络得出的结果基本上都能满足现场实际需求且偏差在0.5℃以内。

2 影响定子绕组出水温度的因素和温度模型介绍

2.1 影响定子绕组出水温度的主要因素有定子电流、定子流量、定子冷却水进水温度、冷氢温度。次要因素有上下层层间线棒温度的影响，铁芯温度的影响。

2.2 温度模型的介绍

指纹系数判断法——俄罗斯学者V.Poljakov 根据经验建立了一种温度水力温度模型：Θi=ai+bi{Θw+Fe/F[ciI2/Ie2+diI/Ie+ei(ΘH2-Θw)]}（1-1）

式中：Θ：定子线棒出水温度，Θw：定子冷却水进水温度，F：定冷水流量

I：定子电流，ΘH2：冷却气体，指纹权重系数：a b c d e

3 预测温度所用的方法介绍

3.1 大数据拟合的最小二乘法温度预测方法

3.2 大数据处理的BP 神经网络预测方法

BP 神经网络是一种误差逆向传播算法，由输入层、隐含层和输出层三部分组成。同层之间各个神经元相互独立、不连接。相邻两层之间所有单元均与上层单元通过权连接。其网络结构图如图1 所示。

图1 BP 神经网络结构图

整个BP 神经网络包含正向传播与反向传播两个过程。当有输入信号正向传播时，信号向前传播到隐含层各节点，此过程信号的传播是逐层递进的，每层都会有相应的权函数、阈值进行变换，最终传至输出各节点。如果实际输出与期望输出之间的误差大于所给精度，误差信号将沿原来的路径由输出层至返隐含层返回至输入层，反向传播直至满足条件为止。

以下是BP 神经网络算法的具体运行流程。在对网络节点权值及阈值等初始化处理后，选取输入参数X={x1，x2，…xd}以及对应的目标输出参数Y={y1，y2，…，y1}。正向传播过程中，隐含层第h 个神经元的输入表达式为：ah=∑di=1μihxi-γh，i=1，2，…d（2）式中，ah为隐含层第h 个神经元的输入；μih为输入层第i 个神经元与隐含层第h 个神经元之间的权值；γh为隐含层第h 个神经元的阈值。进而隐含层第h 个神经元的输出表达式为：

bh=f（ah）（3）式中，bh为隐含层第h 个神经元的输出；f 为激活函数，通常选用Sigmoid 函数。

同理，输出层第j 个神经元的输入与输出为：

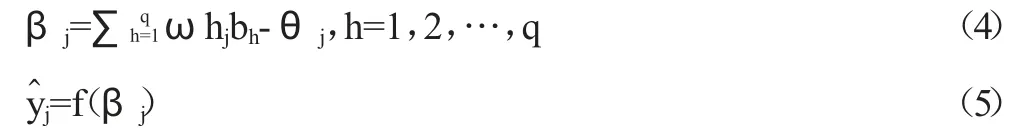
式中，βj输出层第j 个神经元的输入；ωhj为隐含层第h 个神经元与输出层第j 个神经元之间的权值；θj为输出层第j 个神经元的阈值；y^j为神经网络的输出；f 为激活函数。

整个网络需确定d×q 个输入层到隐含层的权值，q×l 个隐含层到输出层的权值，q 个隐含层神经元的阈值，l 个输出层神经元的阈值，经过反复迭代至达到预期精度停止。其中均方误差的计算为：

其中E 为均方误差。

4 某660MW 汽轮发电机定子线圈出水温度预测模型

4.1 模型数据的选取

选取机组大修后不同工况下影响定子线圈出水温度的稳定参数,选取数组为580 组数据其中500 组作为预测数据，30 组为测试数据。

4.2 利用二乘法和公式拟合的方法确定指纹系数，拟合出指纹系数判断法的方程，根据拟合到的方程，将自变量带入方程中得到所需要的因变量。

将指纹系数判断法方程转换成矩阵形式的方程：

Y=@（k，x）k（1）+k（2）*（x（:，1）+100*（k（3）*x（:，3）.^2./（21.17^2）+k（4）*x（:，3）./21.17+k（5）*（x（:，4）-x（:，1）））./x（:，2））;（7）

式中k（1、2、3、4、5）代表a b c d e。x（1、2、3、4）分别代表定冷水温度、定冷水流量、定子电流、冷氢温度。

用500 组数据利用最小二乘法[k，resnorm] = lsqcurvefit（Y，k，x，y） 拟合出指纹权重系数a=31.7063、b=0.3352、c=48.9376、d=9.7566、e=0.8634。将权重系数代入方程得到指纹系数方程，用测试数据和实测数据进行对比的偏差结果。如表1，如图2。

图1 为运用二乘法和指纹系数判断法预测的实测温度和预测温度值

表1 数据建模的样本数据和预测数据

4.3 利用BP 神经网络预测网络模型

因为选取的数据不在一个数量级上，所以对数据进行归一化处理，建立了net=newff（inputn，outputn，[9，1]，{'tansig'，'purelin'}，'trainlm'）神经网络，设置两层隐含层，第一层设置了9 个神经元，第二层设置了1 各神经元，第一层和第二层的激励函数为双曲线正切函数，第二层和输出层之间的激励函数为线性函数。训练函数采用的Levenberg-Marquard（共轭梯度法）优化算法的函数。经过大数据的训练认为该网络满足实际的需求。用测试数据对网络进行预测结果表明实测温度和预测温度偏差最大不超过0.5℃，图3。

图3 神经网络模型预测数据误差分析

5 结论

5.1 采用最小二乘法和指纹系数判断法拟合的指纹系数公式的精确度在0.5℃以内，完全满足现场实际的需求。确定的指纹权重系数有其特定的含义，可以反映出测量通道的固有特性，冷却水管的通畅程度及其测量元件的灵敏度，对各线圈（或各槽）的指纹系数的横向比较，可以诊断出具体的故障类型，避免温度比较法可能产生的误判和漏判，是目前较为实用的一种故障诊断方法，为发电机精准检修提供有力的支撑。

5.2 BP 神经网络采用Levenberg-Marquard 作为训练函数，可以找到全局的最优解，适合于有特定规则的函数模型预测中。

5.3 指纹系数判断法结构清晰，运算简单、明了与神经网络计算结果误差几乎相等，适合运行在现有的监控分析平台中。