基于分离设计与优化的多电机自抗扰协同控制

陈 阳，李 欣

(1.兰州交通大学 光电技术与智能控制教育部重点实验室，兰州 730070；2.兰州交通大学 新能源与动力工程学院，兰州 730070；3.兰州交通大学 甘肃省轨道交通电气自动化工程实验室，兰州 730070)

0 引 言

物质资料的极大需求促使以多电机系统为核心的工业生产的快速发展[1-5]。基于偏差耦合的多电机协同控制策略广泛应用于控制工程中，这种通过特殊的速度补偿器对系统中每台电机转速做偏差的协同控制策略，能将得到的偏差值求和并给予不同的增益补偿以提高电机之间的协同性能。该控制策略能使系统中各电机之间都保持着相互耦合的关系，为了获得更好的协同控制性能，许多学者改进了控制器结构。文献[6]提出误差补偿控制方法，构造出能够判断误差等级的控制器并对误差较大的电机优先给予误差补偿，所设计的控制器结构简单且协同性能较好。文献[7]中提到，传统的偏差耦合控制本质上是在提高单电机的控制性能而非系统整体的协同性能，因此设计了控制器去替换原速度补偿器的分配增益值，并在实物平台上验证了所提方法的可行性。文献[8-9]运用模糊控制、神经元算法分别设计了模糊控制器和神经元PID控制器，所设计的控制器能够根据实际变化情况进行控制，具有很好的协同控制性能。文献[10-11]将反演控制、滑模变结构控制与多电机系统相结合，在减小协同误差的基础上增强了系统的控制性能与开放性。上述文献通过改进控制结构以及同步控制算法实现了良好的控制性能，但改进的控制结构对同步性能的提高不明显，许多算法也未考虑电机运行易受扰动影响的问题。

自抗扰控制技术[12-16]因具有特有的处理非线性、多变量等问题的能力，被应用于控制工程不同领域中。该方法应用到电机控制中可实时估计与补偿转速信号中的扰动，这对于减小同步误差、提高系统协同性能、同时增强系统的抗干扰能力有着重要的意义。自抗扰控制器涉及三部分的设计问题，且这三部分构成的整体起着抗扰的作用，但这三部分内容的设计却是可以单独进行的，即按各自的设计要求分别单独设计各组成部分，继而组合成一个完整的自抗扰控制器，独立设计并组合的过程就是一分离性原理[17]。参考文献[18-21]中将自抗扰控制技术与多电机系统相结合，本文将自抗扰控制技术引入多电机偏差耦合系统中，自抗扰控制器采用分离设计，并用遗传算法对自抗扰控制器核心参数进行优化。仿真结果表明，所设计的控制器能够减小电机间的同步误差值，增强多电机系统的抗干扰性能，实现了非线性的自抗扰控制。

1 偏差耦合的多电机协同系统

图1为偏差耦合的多电机协同控制系统结构框图。图中每台电机的转速会通过速度补偿器得到各电机间的同步误差值，该同步误差值经反馈通道反

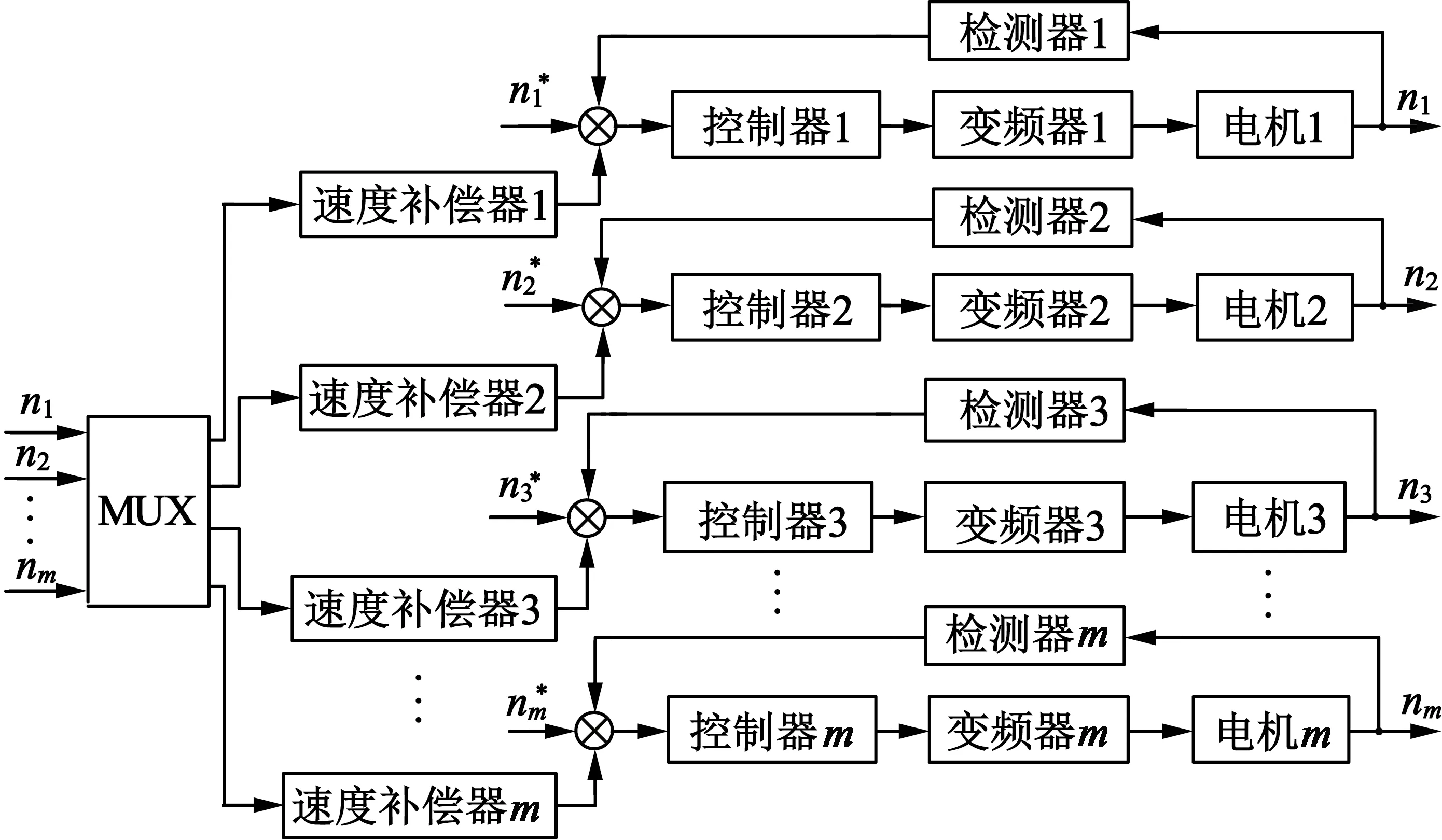
图1 多电机偏差耦合控制框图

馈至每台电机上，对电机的输出转速进行补偿，这便完成了多电机系统速度的实时补偿。同步误差、各电机的速度补偿、同步率的表达式如下：

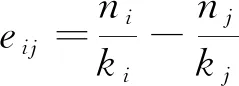
(1)

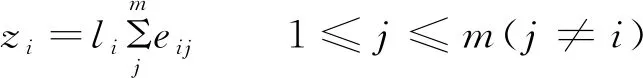
(2)

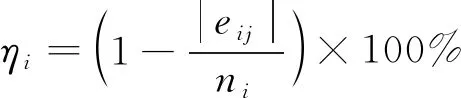
(3)

同步率是衡量多电机协同系统性能的一个重要指标，同步率值越大协同性能越好。由式(3)也可看出，减小同步误差值就能增大同步率，因此改善多电机的协同性能就需要尽量减小同步误差的绝对值。

2 自抗扰控制器的工作原理及分离设计

2.1 自抗扰控制器工作原理

在多电机系统中，电机会受到相互之间耦合关系、自身转动惯量以及外部负载等诸多因素的影响，这导致多电机系统的协同能力不强，抗干扰能力弱，协同性能得不到保证，因此改善系统协同性能的第一任务便是增强系统抗干扰性能。自抗扰控制器能够抑制转速偏差值中的扰动信息，或者说速度补偿器的输出中所含扰动信息是可被观测的，那么就能从所观测扰动信号中提炼出扰动作用并进行相应的补偿。

其中跟踪微分器完成系统的过渡工作并随时提取微分信号。非线性状态误差反馈，是将跟踪微分器产生的误差信号、误差微分信号和误差积分信号组合起来。扩张状态观测器在对系统的输出量观测时，不用考虑被控对象的精确数学模型，同时与非线性状态误差反馈率共同作用，对扰动进行补偿。

图2为自抗扰控制器的结构框图。

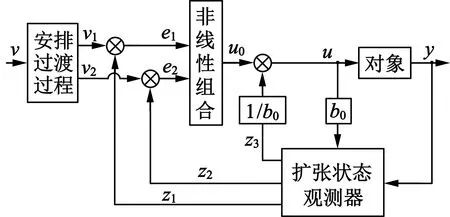
图2 自抗扰控制结构

自抗扰控制器算法如下：

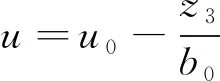
2.2 自抗扰技术的分离设计

上述自抗扰控制器在理想状况下有良好的效果，但其复杂的算法以及过多的计算量在结合多电机系统时，使得系统运行时间变长，控制性能下降，控制器要调节的参数变多，因此对自抗扰控制器进行改进，简化控制器模型、减少控制参数是很有必要的。

跟踪微分器主要依据设定值获得微分信号与过渡过程的相应安排，反馈信息中若没有该微分信号，则没有微分项输出，因此可将微分跟踪环节省去。

非线性状态误差反馈需根据控制器阶数设计，本文观测变量为电机转速，即控制器为一阶，所以此处将非线性状态误差反馈用线性比例增益替代，可通过改变增益值获得与非线性状态误差反馈相近的效果，此外还可以有效地降低模型复杂程度，减少计算量。

扩张状态观测器利用扩张的新变量代替扰动变量，再根据原系统输入输出关系对系统所有变量进行观测，其控制器设计是根据受控对象的数学模型进行相应设计,图3为自抗扰控制器分离设计结构框图。

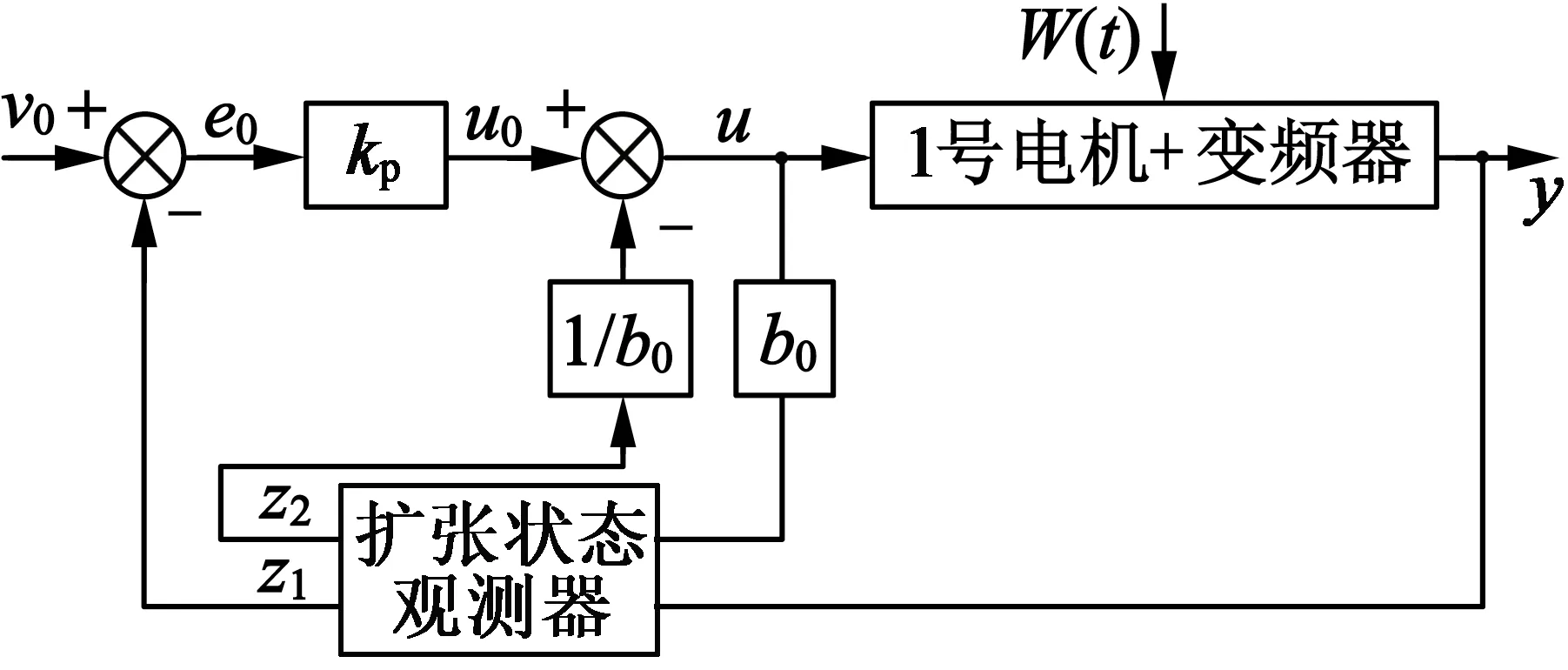
图3 自抗扰控制器分离设计结构框图

图3中：v0为系统输入;y为系统输出;z1是y的观测信号;z2为扰动的观测信号;u为系统的控制量;kp为比例增益;b0是补偿因子。

由图2与图3比较可得，优化的结构去掉了不必要的非线性微分跟踪模块，非线性模块由线性模块所替代，优化后的模型算法如下：

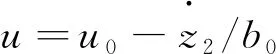
各个部分的独立设计完成以后，就要对各部分进行组合，即在微分跟踪环节去掉后，剩余线性增益kp、状态误差反馈补偿因子b0和扩张状态观测器三部分的组合。需要注意控制器三部分的协调设计。如果b能够算出值，取b0=b；当b未知时，取b真值附近的值。b0，kp的取值在相对误差的30%之内不会影响控制效果。

3 单电机转速环的自抗扰控制器设计

异步电机矢量控制系统的数学模型如下：

由微分方程可得，转速系统与转矩、负载相耦合，因此在设计自抗扰控制器时将转矩的耦合影响视为系统的内部扰动，负载产生的扰动视为外部扰动。由此，根据上述微分方程可建立相应的扩张状态观测器。令x1=ω，那么：

根据上式可知，相应电机的一阶自抗扰控制器数学模型如下：

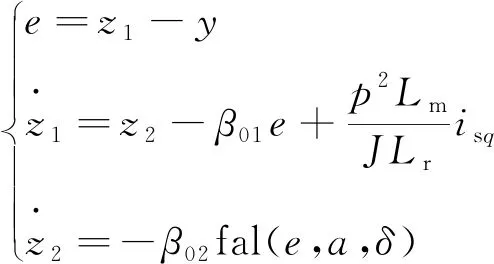
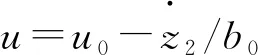
其中的fal函数表示：

式中：e为系统误差跟踪值； fal(e,a,δ)为最优控制函数；a为0～1的非线性因子；δ为滤波因子；β01,β02为状态观测器误差增益；ω0为初始速度给定值；kp为比例增益值。

4 自抗扰控制器参数优化

自抗扰控制器的核心是扩张状态观测器，其控制性能主要受控制器参数的影响，如果控制器结构确定，那么合理选取控制参数会使自抗扰控制器产生较好的适应性和鲁棒性。通常情况下，控制器的参数整定需要操作者有丰富的现场控制知识和经验，根据经验法获得控制参数耗时耗力，尤其是在进行优化时，所得目标函数要获得最优值且不会陷入局部最优解。而遗传算法恰适合观测器的参数优化，用该优化算法对控制器误差增益进行全局搜索，只要能够获取目标函数，控制器的参数优化就易于实现。

图4为遗传算法的流程图，产生的初始种群经适应度值的计算判断是否需要退出进化，是则退出，并获得最优个体值，否则使种群进化一代，同时进行绘图并判断终止条件。

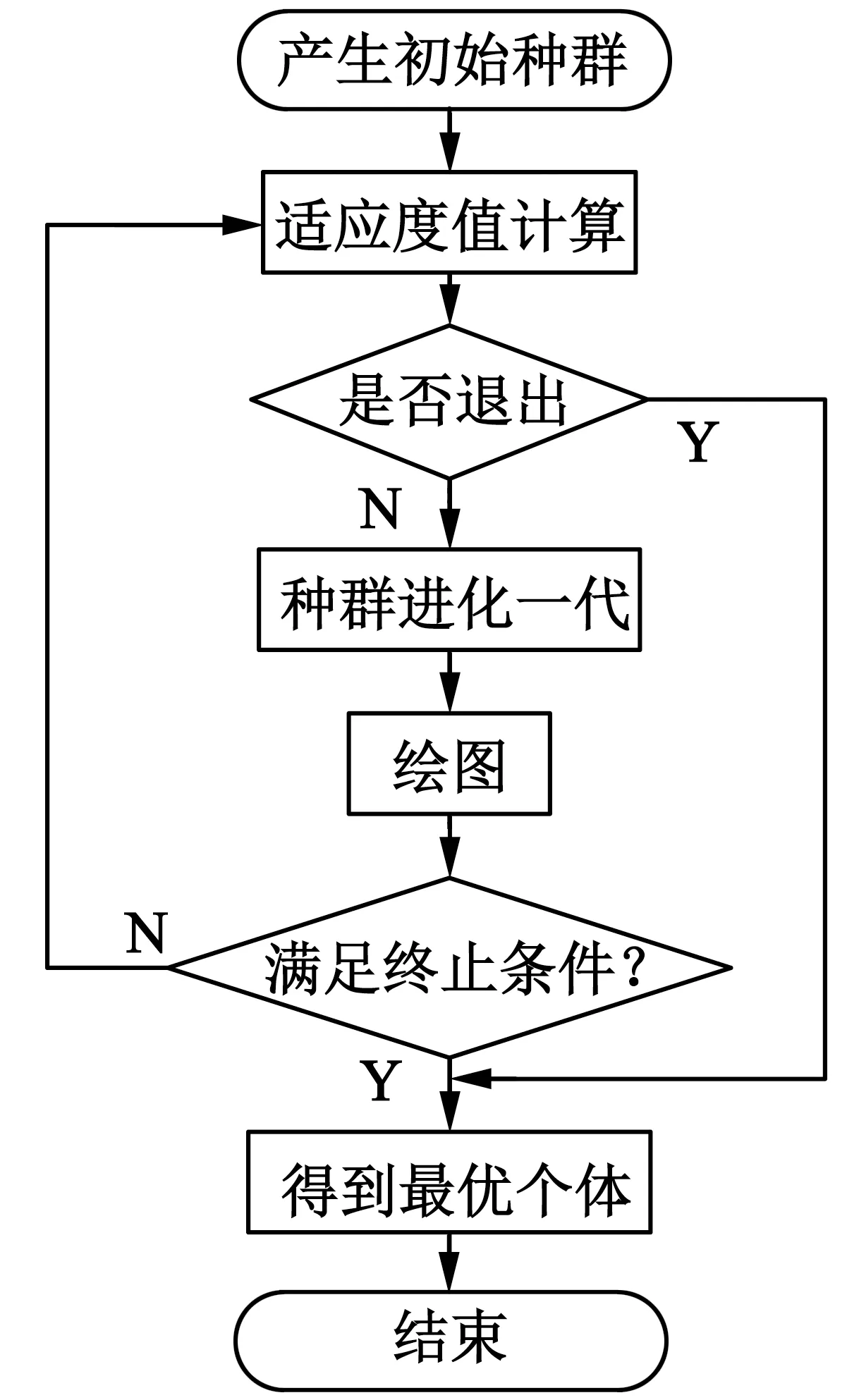
图4 遗传算法流程图

根据前文一阶自抗扰控制器数学模型可知，系统输出与给定值的误差绝对值的积分越小，协同性就能越好。目标函数为误差性能指标IAE(绝对值误差积分)：

图5为适应度函数值变化曲线和最优个体值。由图5可以看出，随着种群代数的不断迭加，适应度函数值越来越小，运行得到误差值e=0.063，β01=4 999.9，β02=9 850.3。

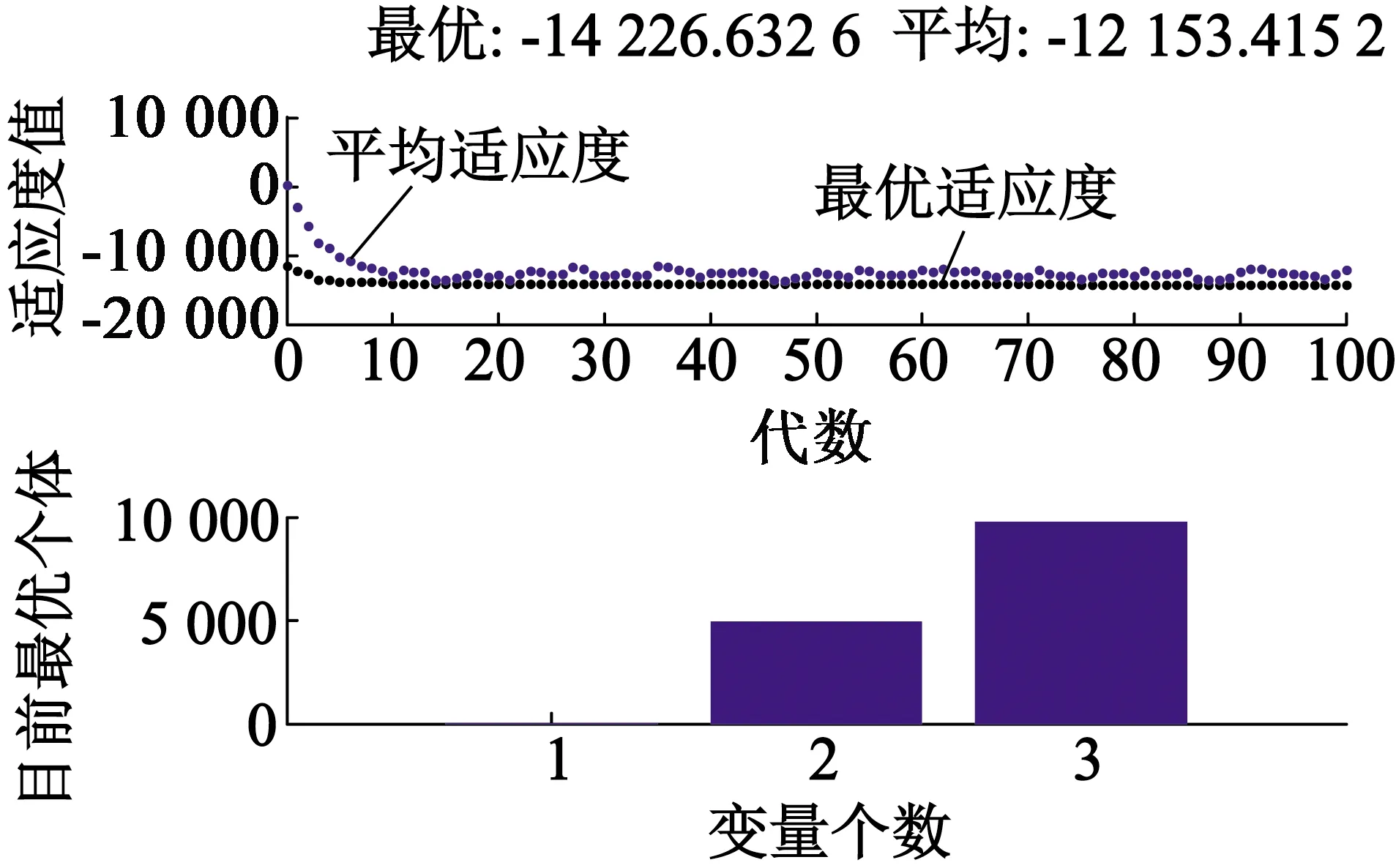
图5 适应度函数变化曲线和最优个体

偏差耦合的多电机系统是通过做偏差建立电机间相互关系的，而单台电机的控制性能会直接影响控制系统的整体性能，所以多电机协同系统根本上还要提高单台电机的控制性能。此外多电机系统中的各电机控制方法与参数设置一致，因此将单台电机自抗扰控制参数优化结果用于系统中的每台电机上，通过提高单电机性能以改善系统整体性能，也同时适合三台电机。

5 仿真分析

5.1 仿真参数

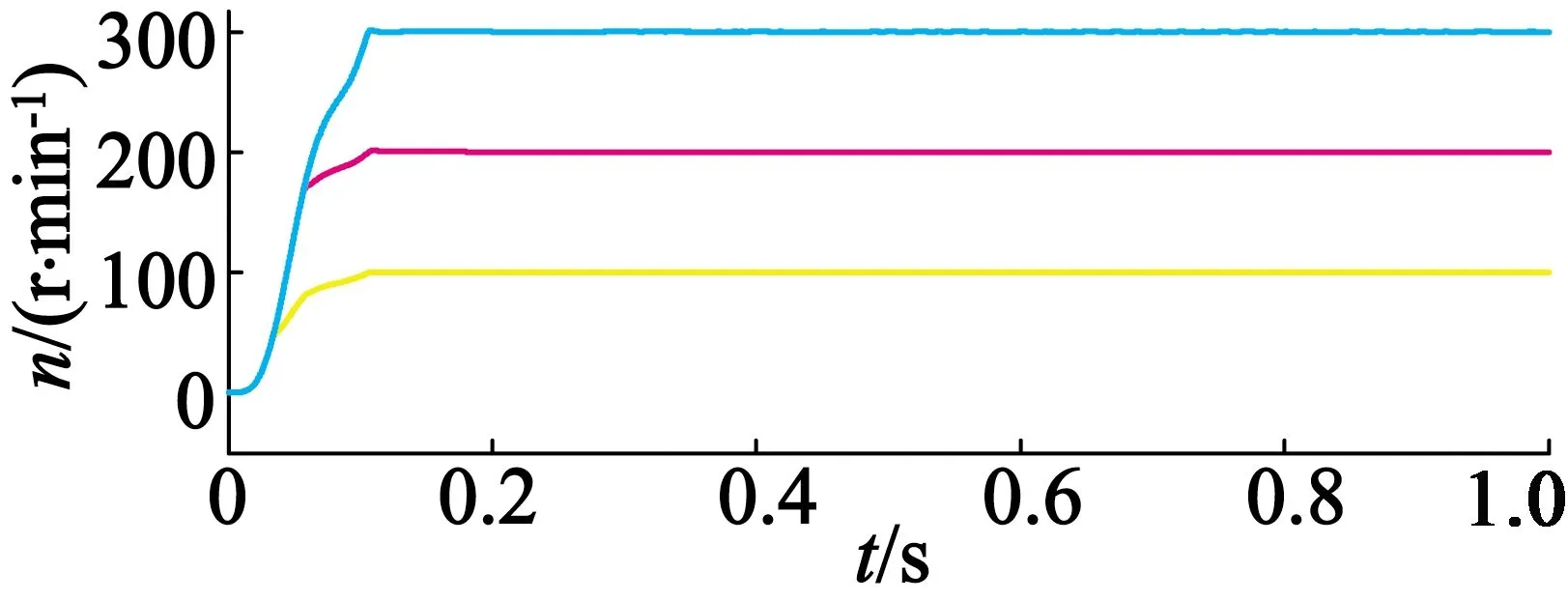
本文选取三台三相异步电机，运用MATLAB/Simulink仿真软件，构建三电机协同控制系统模型。基于自抗扰的三电机偏差耦合控制系统中，各电机转速值设定与图6一致，在0.45 s时，系统会对第一台电机突加60 N·m的负载。表1为电机各项参数，图6为三台电机协同系统总体仿真建模的框图。

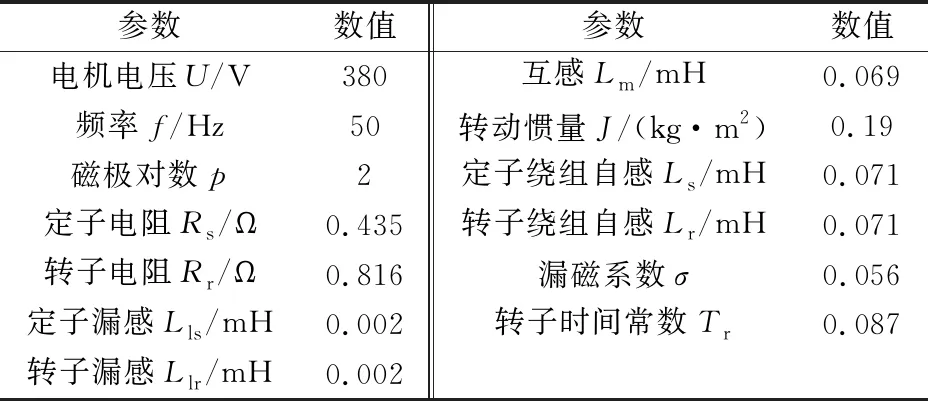
表1 电机参数

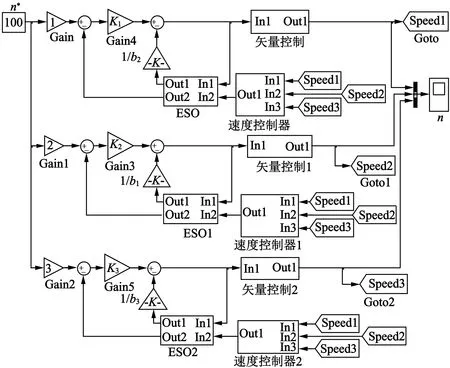
图6 三电机协同系统仿真建模框图

5.2 仿真结果及分析

5.2.1 抗扰性能分析

图7(a)为未加自抗扰控制器且无扰动时的三电机转速波形图，图7(b)为未加自抗扰控制器但加有负载扰动时的三电机转速波形图。由图7(b)可看出:在0.45 s时，由于加载了负载扰动，所以在同一时刻三台电机的转速会同时下降，经过短暂调整转速又达到给定转速；在0.51 s和0.6 s时出现的未知扰动属于模拟扰动，并且扰动较大，转速下降较为明显。由此可认为在本系统中未知扰动是主要的扰动因素。图8为加自抗扰控制器的电机转速波形图。仿真结果表明，在0.51 s和0.6 s时的转速未发生波动，所设计的自抗扰控制器有效地抑制了扰动的影响。在0.45 s时对系统加载60 N·m的负载扰动，由于这个扰动是突加的，控制器难以及时补偿，只能在一定程度上减小对转速的影响。

与此同时，图9、图10分别为未加自抗扰与加自抗扰控制器时电机1的转矩波形图。可以看到，图9在0.45 s、0.51 s和0.6 s时转矩波动比较大。图10的转矩波动是0.45 s突加负载时相应的波动，其他未知的扰动经自抗扰控制器后被消除了，由此可认为所设计的自抗扰控制器抗干扰性能较强。

(a) 无扰动

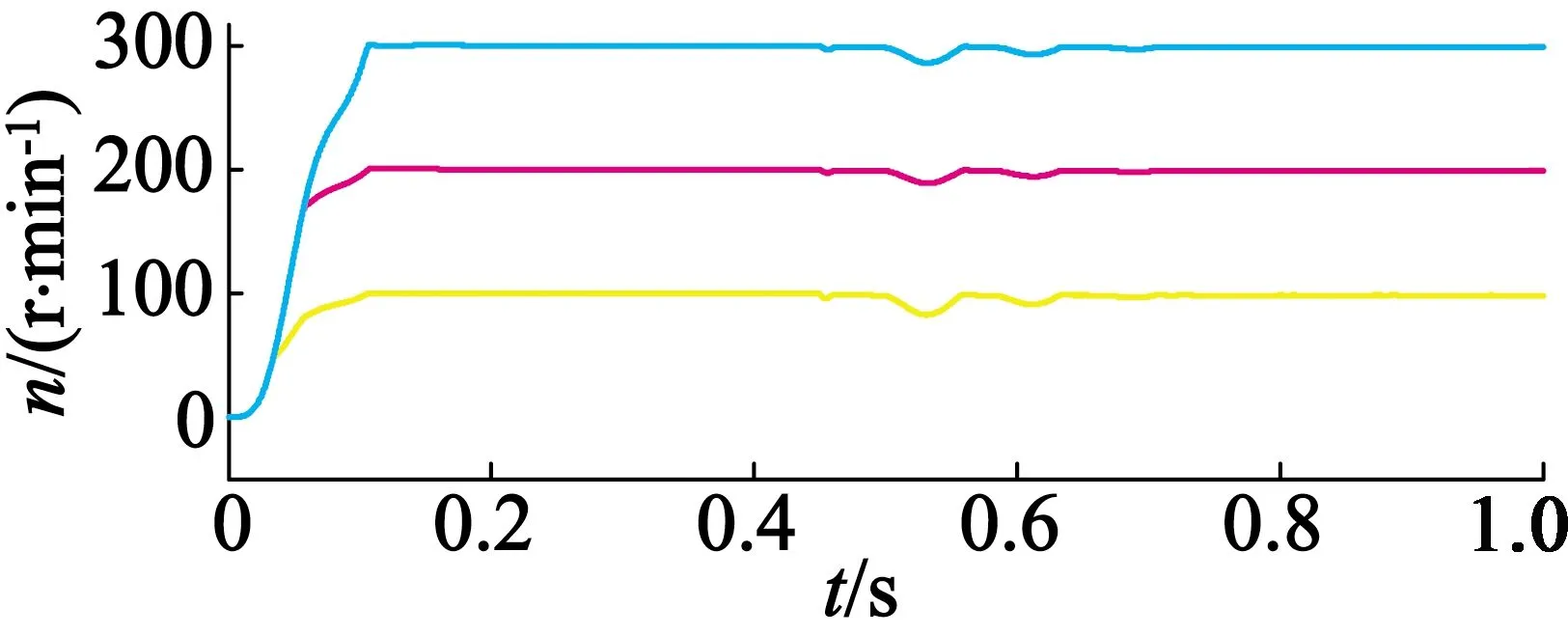
(b) 有扰动

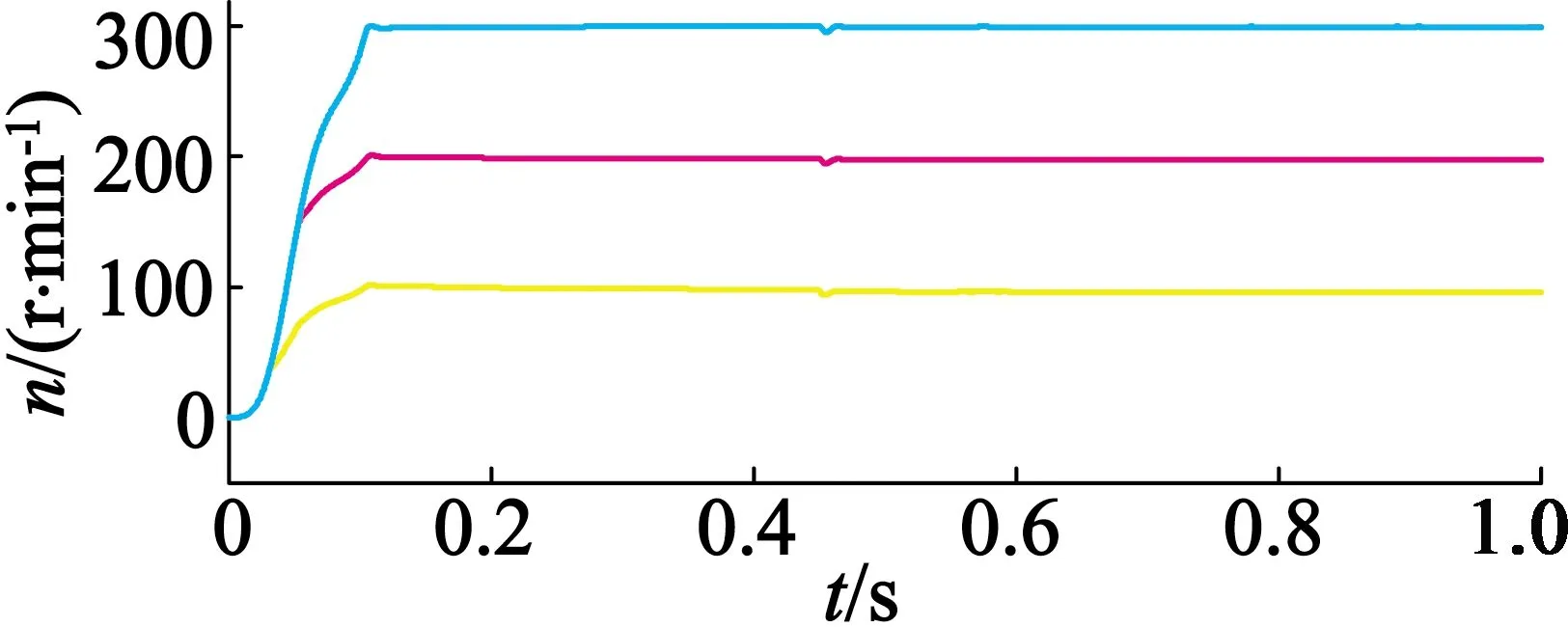
图8 基于自抗扰的三电机转速

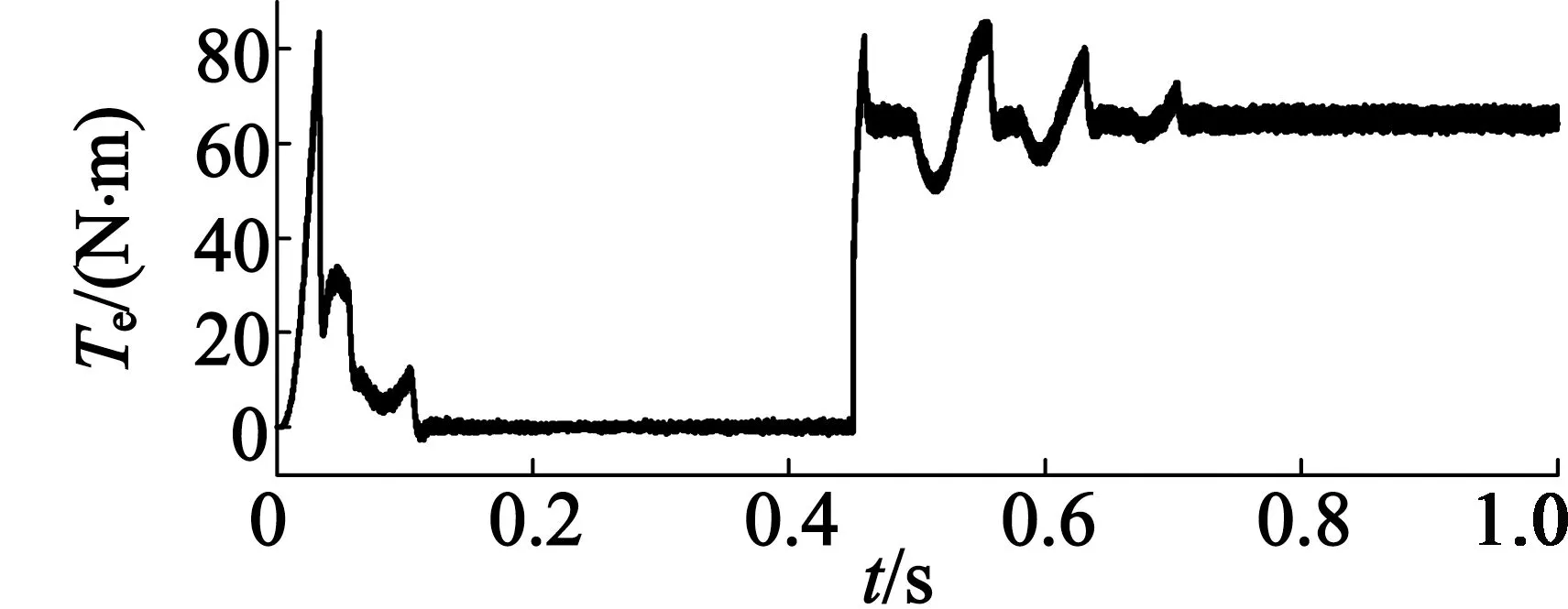
图9 未加自抗扰电机1转矩

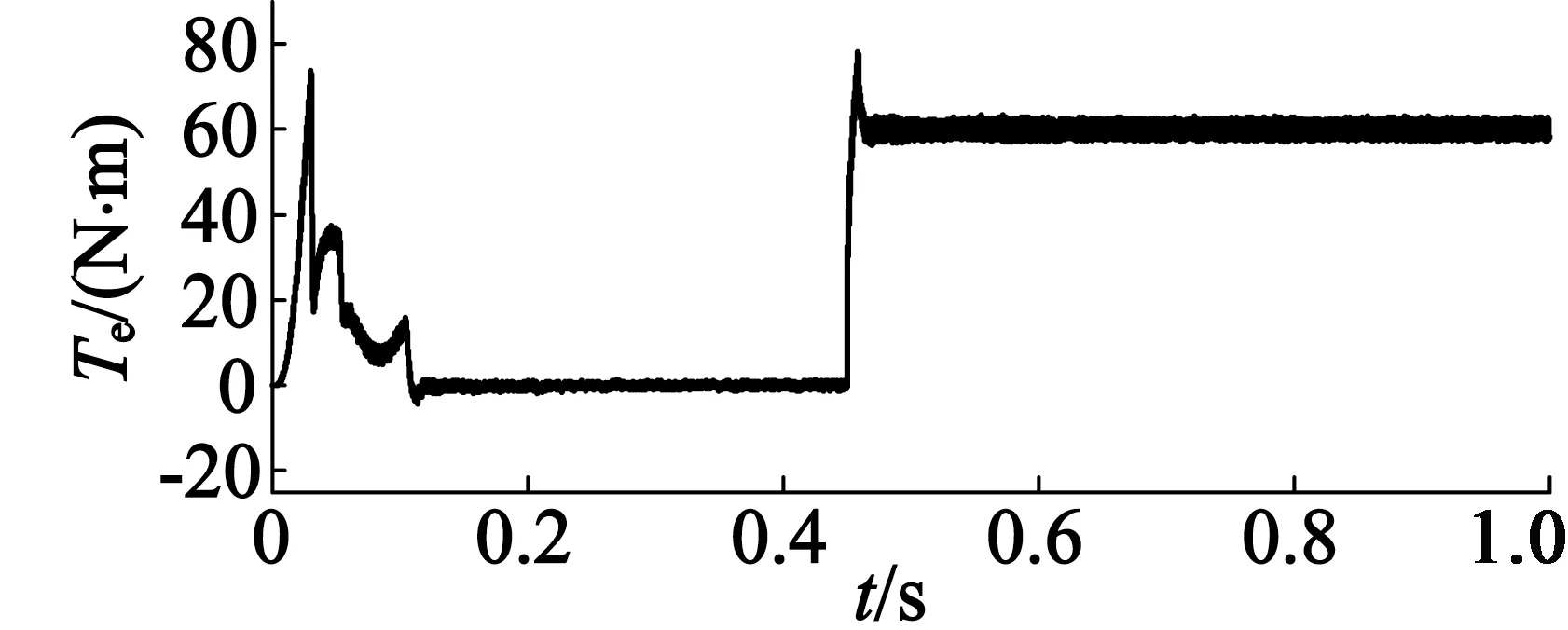
图10 基于自抗扰电机1转矩

5.2.2 协同性能分析

电机之间的同步误差值大小体现出多电机系统协同性能的好坏，误差越小则协同性能越好。以电机1的速度补偿器为例，如图11所示，未加自抗扰控制器时电机1与电机2间的同步误差最大值为22.8 r/min，并在短时间内稳定到0；在0.45 s，0.51 s和0.6 s受到扰动的影响，两台电机间的同步误差也在相应地不断变化，经过调整，同步误差值最终稳定在1.2 r/min。与图12相比，加自抗扰控制器后电机1与电机2开始时同步误差值减小至17.7 r/min，并在短时间内将误差值调整至0附近，从图12中可以看出，同步误差曲线的变化除受到突加负载的扰动之外，其他未知扰动的影响已经被消除，同步误差值最终稳定在2.6 r/min。图13与图14为电机1与电机3之间的同步误差仿真图。与电机1和电机2的分析方法一致，此处不再赘述。由此可得，自抗扰控制器不仅有较好的抗扰性能，而且在偏差耦合的多电机系统中能够进一步地提高电机间的协同性能。

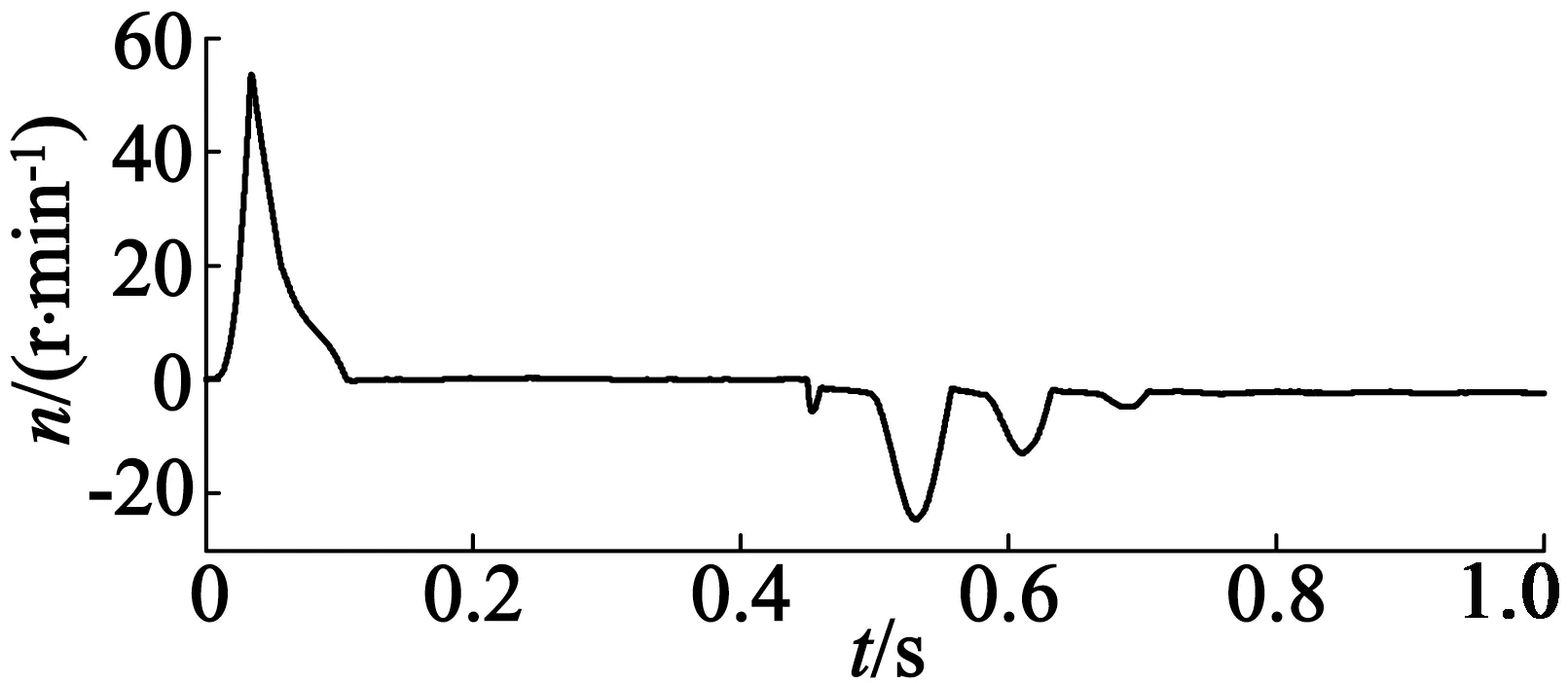
图11 未加自抗扰同步误差e12曲线

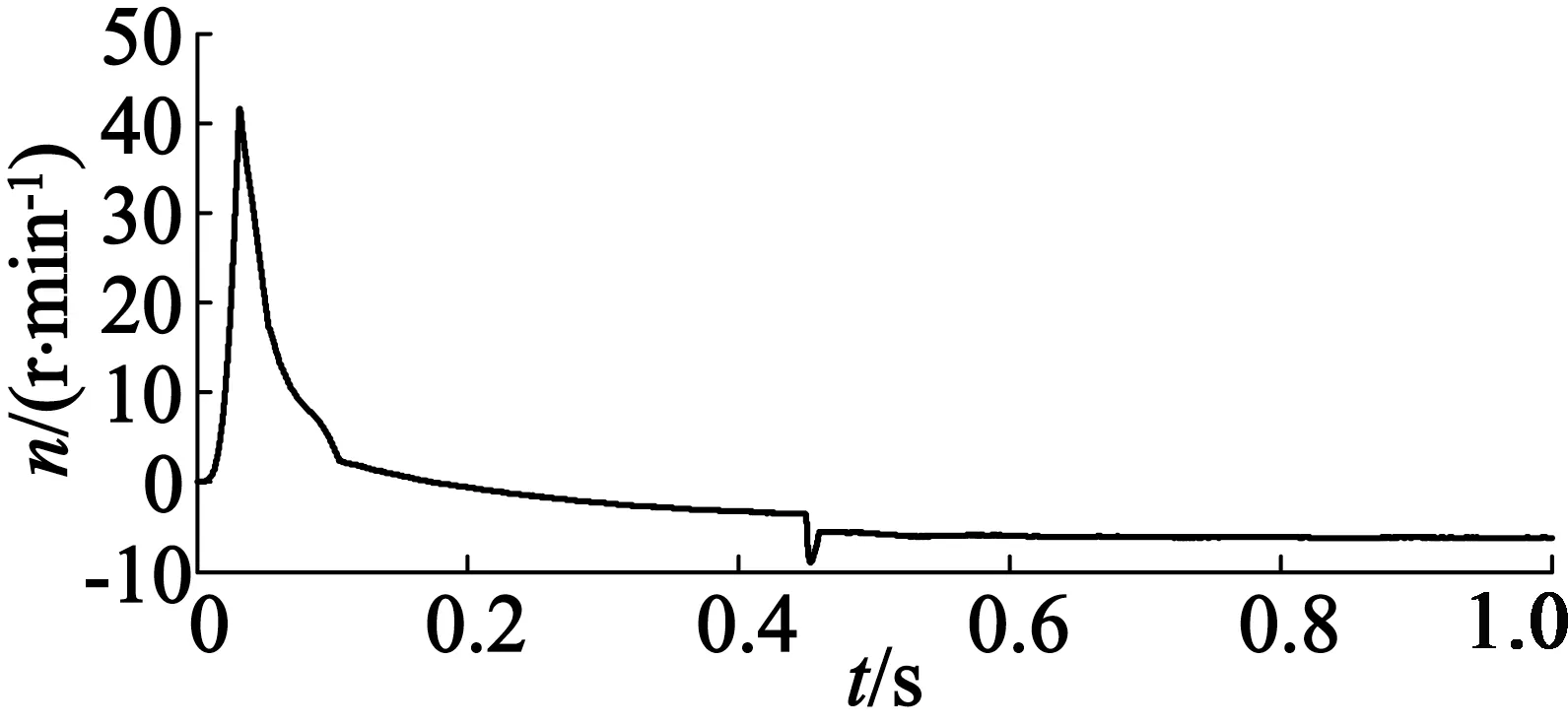
图12 基于自抗扰的同步误差e12曲线

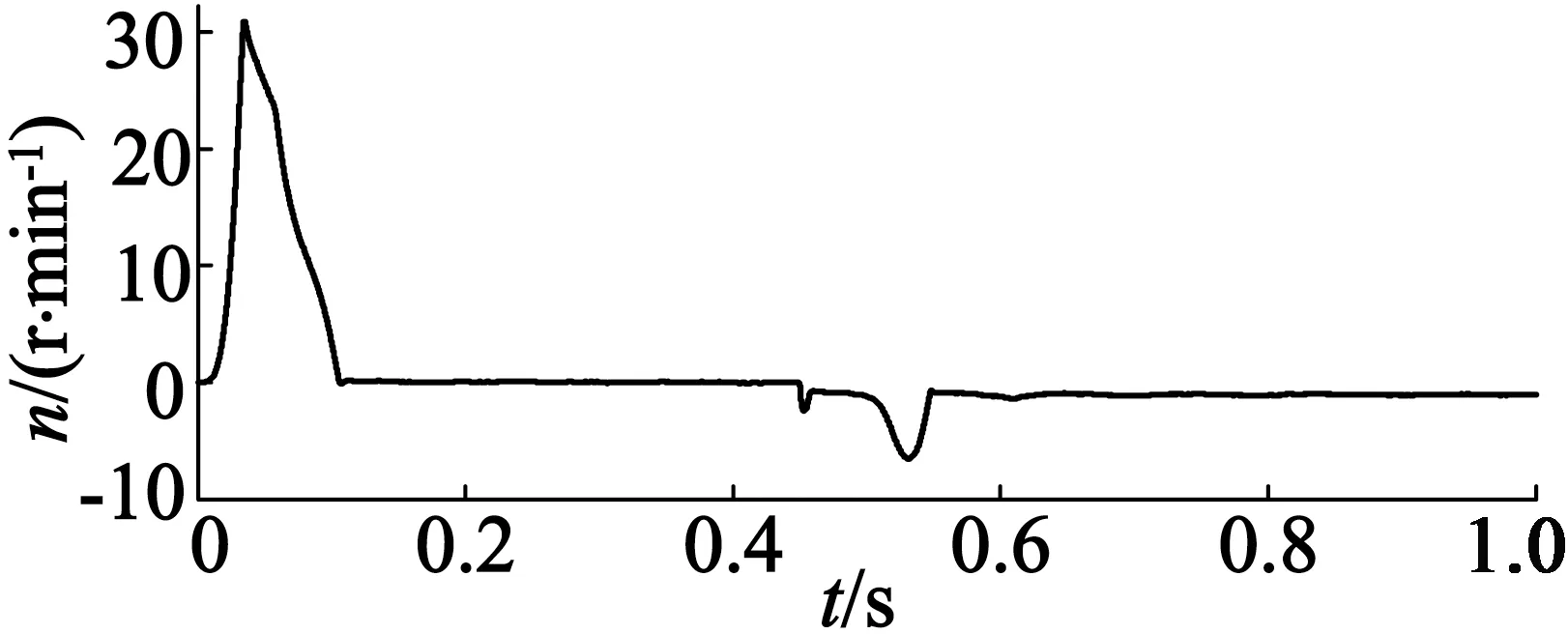
图13 未加自抗扰同步误差e13曲线

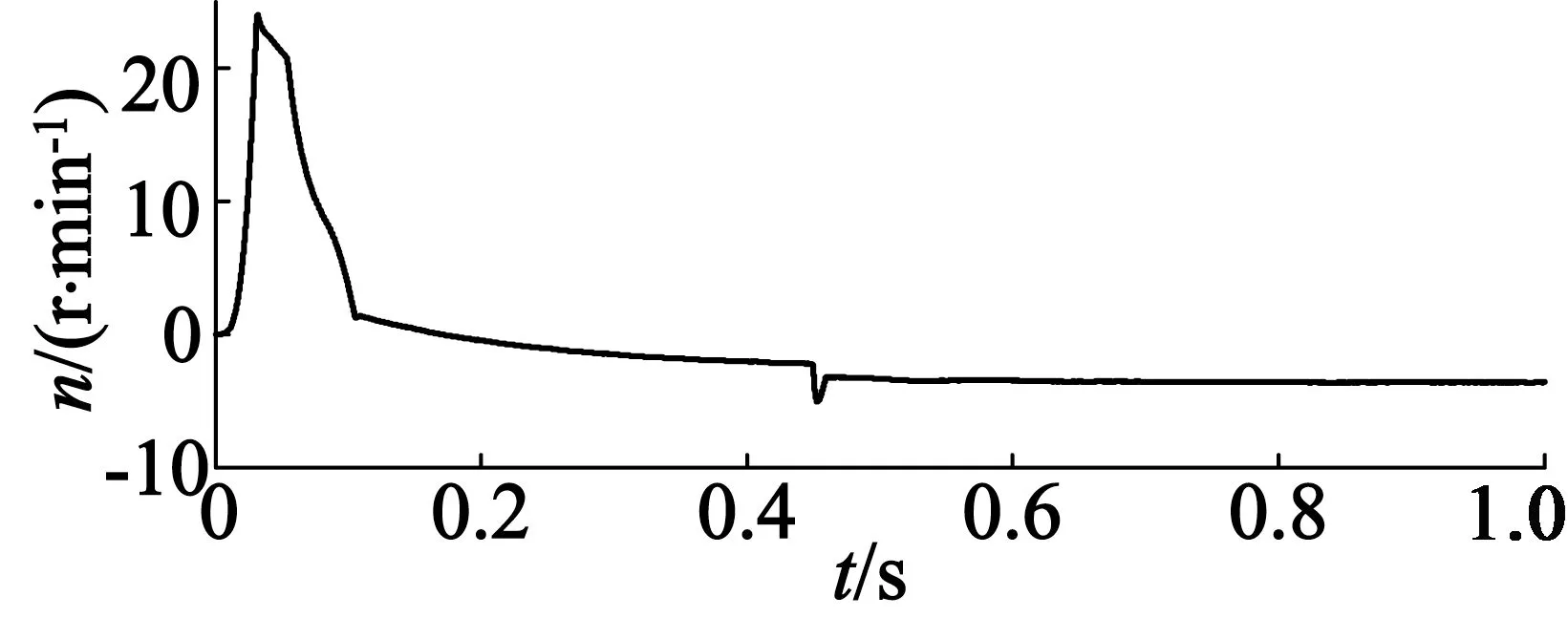
图14 基于自抗扰的同步误差e13曲线

6 结 语

针对采用偏差耦合控制的两电机系统实际运行中电机间的耦合影响以及系统内外扰动作用对电机转速、转矩的影响，引入的自抗扰控制器，可以将系统中的扰动因素从误差信号中观测出来，并进行相应的误差补偿，控制器设计也无需被控对象精确模型，同时还提高了系统的鲁棒性和抗干扰性。自抗扰控制器的分离设计是根据多电机系统误差进行的，当误差发生变化时，可相应地改变自抗扰控制器参数进行调整，实用性较强。