基于模糊多态共因失效因素的矿井提升制动系统故障诊断

王晓军，王家琦，李汝楠，王 凯，杨春霞

1太原科技大学 山西太原 030024

2广西柳工机械股份有限公司 广西柳州 545007

矿 井提升机负责提升井下矿物、工作人员以及施工材料，是矿业生产中重要的运输设备。提升机制动系统直接关系到设备的安全运行。G.Bertrand 等人[1]从风险分析的角度阐述了制动系统属于矿井提升设备常见安全风险；M.Zhang 等人[2]和 G.Laurent 等人[3]均用故障树分析了相关历史数据，给出导致矿井事故发生的常见原因，其中包括制动系统失效。因此，对制动系统进行故障诊断分析有重要的现实意义。

在相关研究中，韩瑞东等人[4]将贝叶斯网络引入矿井提升制动系统故障树分析，采用概率反应事件严重程度，通过增加网络节点来分析故障事件的多态性，并建立了相应贝叶斯网络模型。田晓翠[5]将模糊数学理论引入故障树分析，将不确定性问题模糊化处理，采取模糊数概率代替一个确定的概率数值。樊忠[6]针对提升机制动系统故障诊断中的知识获取和知识推理等关键技术，将粗糙集、MATLAB、贝叶斯网络和改进启发式搜索算法相融合，给出了相应故障诊断方法。上述研究从一定程度上解决了矿井提升系统的模糊性和多态性，但在对基本事件处理上，仍然默认先验概率为确定值，没考虑先验概率的模糊性，同时对系统及零部件引发的共因失效问题涉及较少。

共因失效是指在系统中由于某种共同原因而引起 2 个或 2 个以上单元的同时失效。国内外学者对共因失效模式下贝叶斯网络建模的理论方法及应用已经有了不少的研究，在柴油机冷却系统[7]、牵引变电所系统[8]、接触网[9]、海底油气井防喷器系统[10]、GOFLOW 模型[11]等领域都有研究进展，但鲜少能看见在矿井提升领域中的应用。综合前面对矿井提升系统故障分析，笔者认为有必要在综合考虑模糊、多态及共因失效 3 种因素的基础上，对矿井提升制动系统进行故障诊断分析及应用研究。

1 制动系统的故障树

根据以往资料，矿井提升机制动系统故障主要为制动器和液压系统失效。

1.1 制动器失效

(1)制动力矩不足，主要原因为摩擦因数过小、闸瓦磨损过多、正压力不足；

(2)闸失效，主要原因为制动缸卡缸、盘形闸液压缸漏油以及液压站故障等。

1.2 液压系统失效

(1)液压系统压力不稳定，主要原因是溢流阀堵塞；

(2)液压油达不到要求，主要原因是液压油路泄漏或电磁换向阀故障；

(3)液压系统没有油压，主要原因可能是溢流阀故障、吸油过滤嘴堵塞、油泵故障。

通过故障事件分析，建立顶事件T的故障树如图1 所示。故障树中各代号含义如表 1 所列。

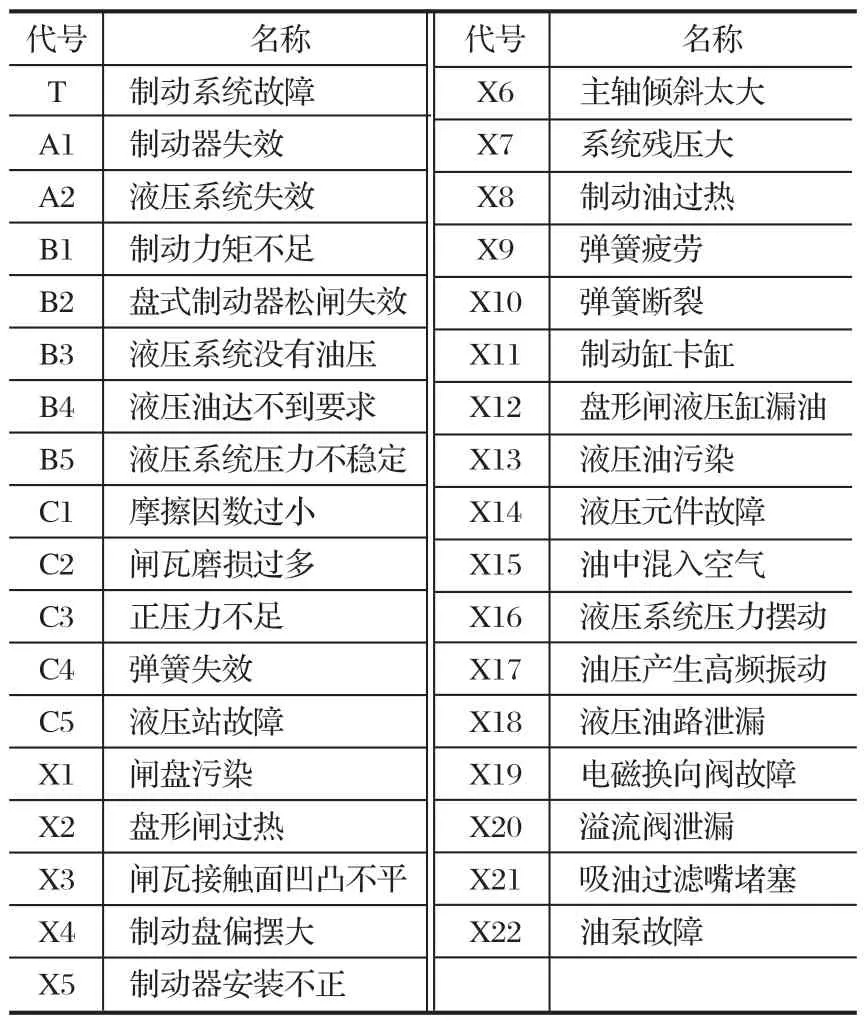
表1 基本事件代号及名称Tab.1 Codes and names of basic events

2 考虑模糊多态共因失效因素的故障诊断

2.1 模糊贝叶斯网络建模

由于环境因素以及人为不确定因素的影响，使得各基本事件的先验概率具有一定的模糊性。此外，对于部分零部件具有小样本事件，或零部件的维修数据较少甚至维修数据丢失的情况，使得该零部件的先验概率也很难用具体确定值表示，往往采用模糊先验概率来表示。模糊先验概率通常用三角模糊数来表示，其函数形式如图 2 所示，其函数表达式如式 (1)所示，其中r为模糊集中心，a、b分别为模糊上下限。

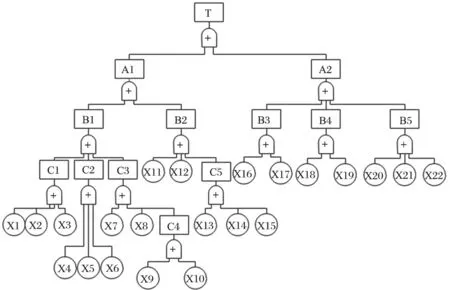
图1 矿井提升机制动系统故障树Fig.1 Fault tree of braking system of mine hoist

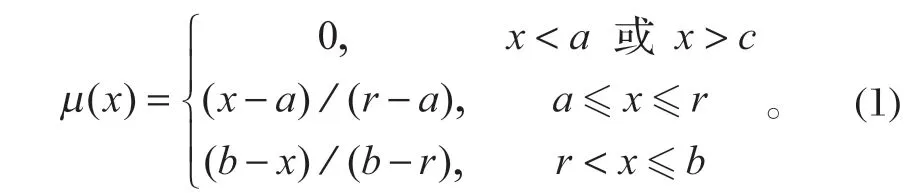
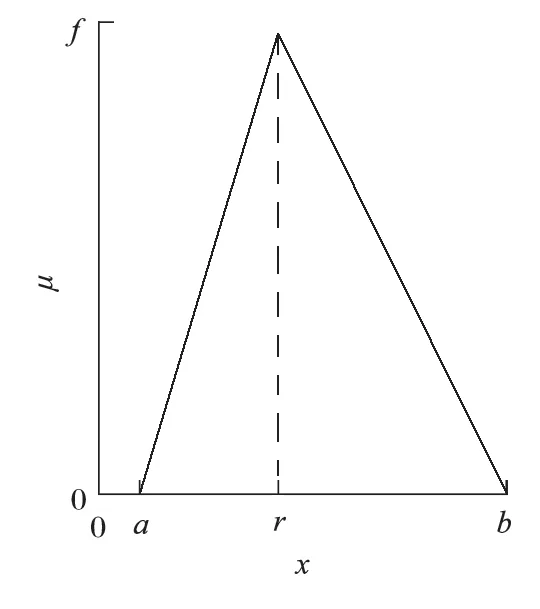
图2 三角形隶属函数Fig.2 Triangle membership function

三角模糊数有如下运算法则：

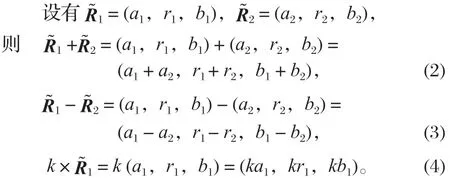
2.2 多态性的表达

贝叶斯网络对于多态性的表达较简单，其不必向故障树模型那样通过增加节点的数目来表达事件的多态性，贝叶斯网络只需修改相应的条件概率表和各故障状态的先验概率即可表达事件的多态性。多态 BN条件概率如表 2 所列。表 2 中每 1 列都表示 1 条规则，m为不同故障状态数，n为根节点数，不同行表示不同的规则。例如第 3 行的规则是：在根节点x1，x2，…，xn-1都处于正常状态，且xn处于完全故障的条件下，叶节点y处于y1，y2，…，ym状态下的故障概率分别为a3,1，a3,2，…，a3,m。

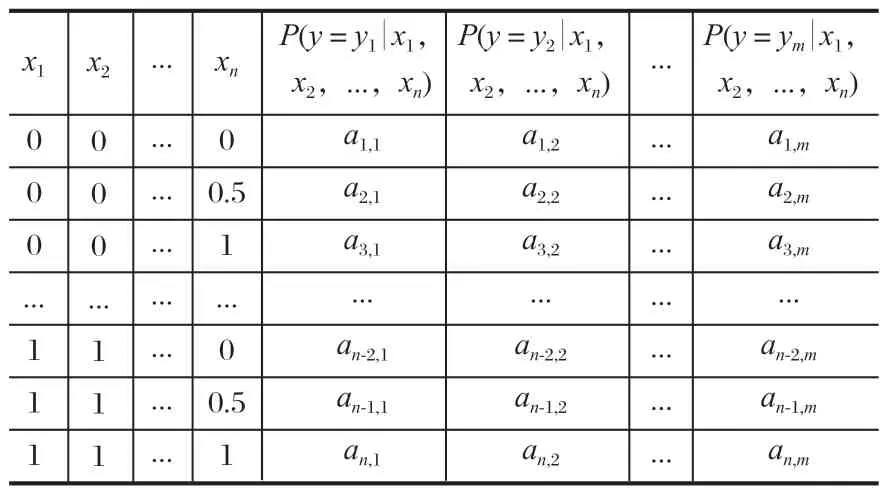
表2 多态 BN 条件概率Tab.2 Conditional probability of polymorphic BN

2.3 共因失效模型建立

处理共因失效问题的分析模型主要有基本参数模型、α-因子模型、β-因子模型以及二项失效率模型等。笔者研究的内容主要是运用β-因子模型求解相应的共因失效问题。其参数β为共因失效因子，是相关失效率与组件总失效率的比值[8]。

设QC为共因失效率，Qt为总的失效率，QI为独立失效率，则参数

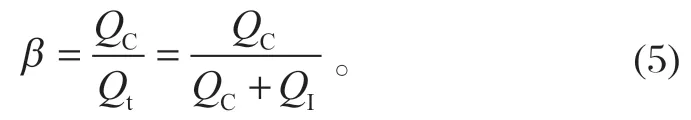
由于与时间相关的失效服从指数分布，且故障率的数值较小，因此

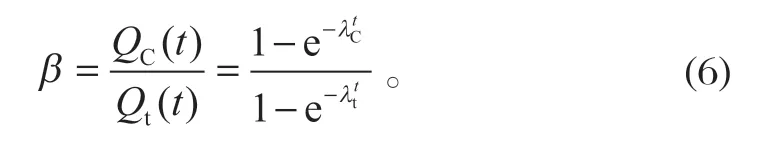
在求解共因失效的β-因子模型时，不仅要考虑共因部件的独立失效部分 (故障率λ1)，同时也要考虑共因失效部分 (故障率λ2)，总的故障率λ=λ1+λ2。因此，共因失效因子

2.4 贝叶斯网络可靠性分析

贝叶斯数学计算公式能清楚地表达先验概率和后验概率之间的关系，事件的后验概率

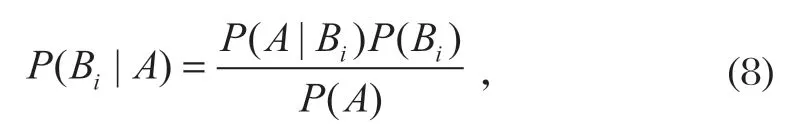
式中：P(A|Bi)为似然概率；P(Bi)为事件的先验概率。

概率重要度反映的是底事件发生故障时对顶事件故障发生概率的影响大小，其计算公式为

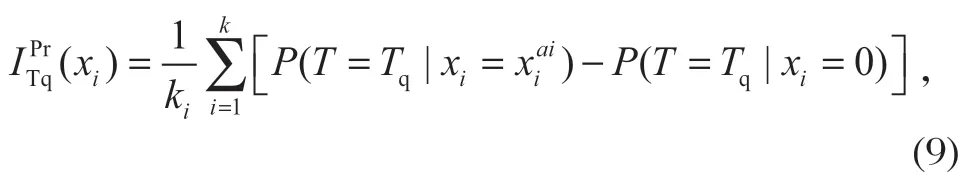
式中：ki为xi的故障状态不为 0 的个数；xi为根节点，其当前故障状态为；T为叶节点，其故障状态为Tq。

3 实例分析

以矿井提升制动系统的子系统液压系统为例，对上述方法进行分析。液压系统故障主要是由于液压系统失效，液压系统没有油压或液压系统的油压达不到制动要求等造成，各基本事件的故障概率和β值如表3 所列。假设各基本事件故障状态为 0.5 的故障概率和故障状态为 1 的故障概率相等，同时假设 X6 吸油过滤嘴堵塞，X7 油泵故障只有 2 种故障状态。运用Netica 软件绘制相应的贝叶斯网络故障树图，其可靠性分析如图 3、4 所示。

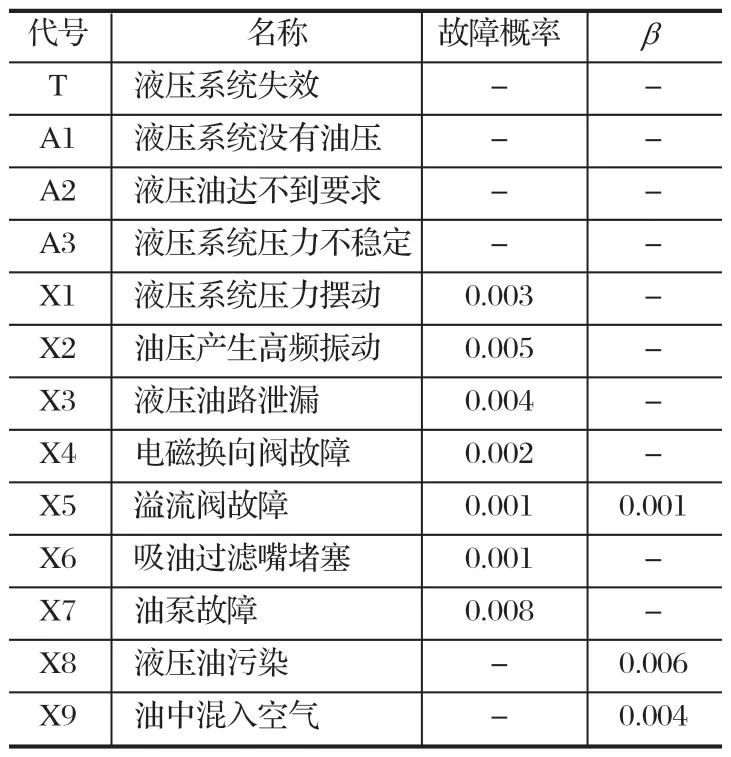
表3 基本事件先验概率Tab.3 Prior probability of basic events

由图 3、4 对比可知，考虑共因失效时，液压系统处于“半故障”状态的故障概率从 0.011 9 上升到0.033 9，液压系统处于“完全故障”状态时的故障概率从 0.023 9 上升到 0.048 4。

对比图 3、4 运用 Netica 软件计算顶事件的结果可知，考虑共因失效时顶事件的故障概率较不考虑共因失效时顶事件的故障概率有所提高，计算结果符合实际情况。

由式 (9)计算各根节点的重要度，在考虑共因失效和不考虑共因失效 2 种状态下，各根节点处于“半故障”状态和“完全故障”状态时顶事件故障概率对比如图 5 所示。

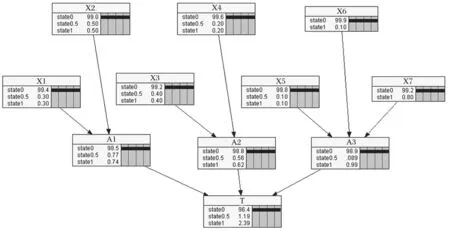
图3 不考虑共因失效可靠性分析Fig.3 Reliability analysis without considering common cause failure

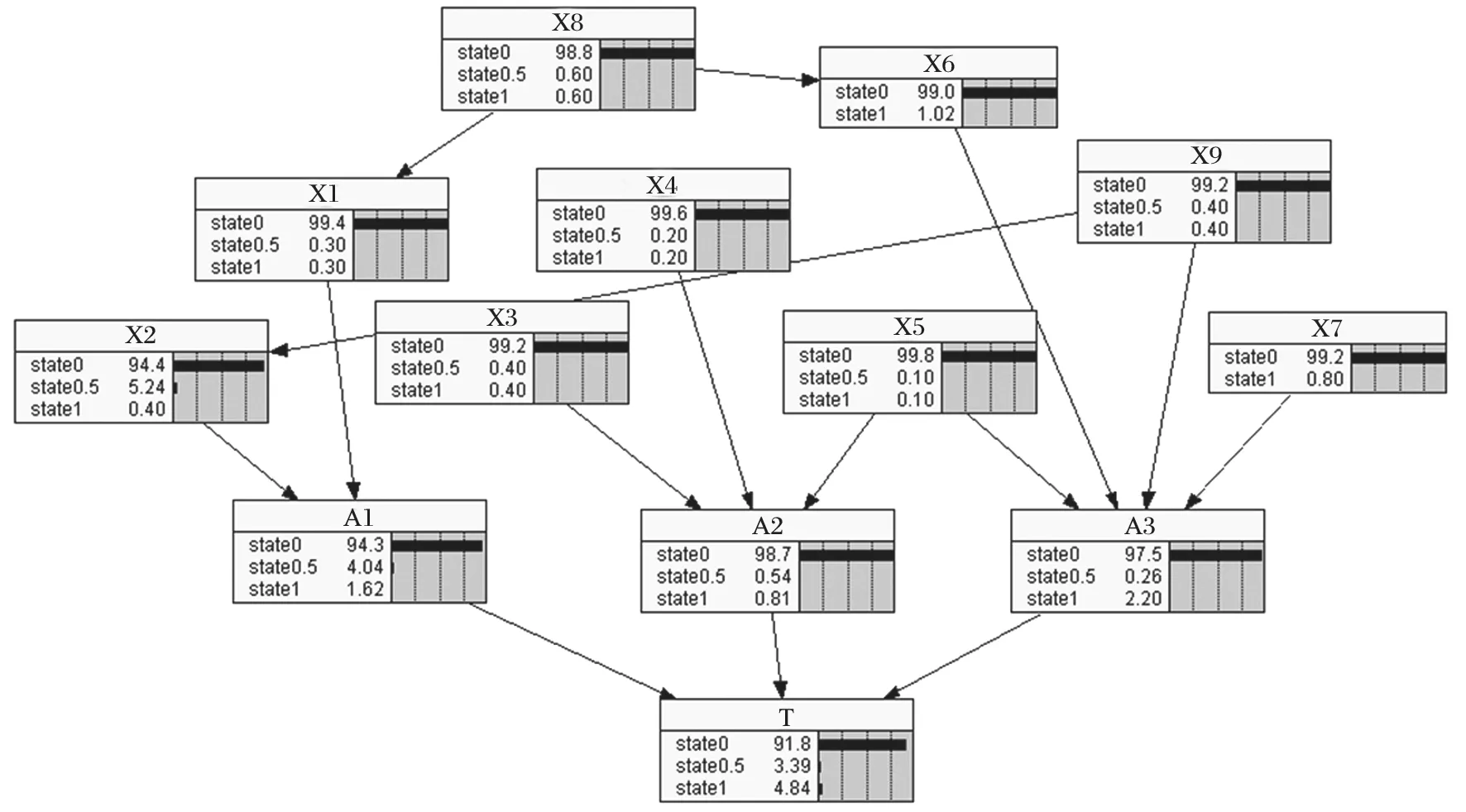
图4 考虑共因失效可靠性分析Fig.4 Reliability analysis considering common cause failure

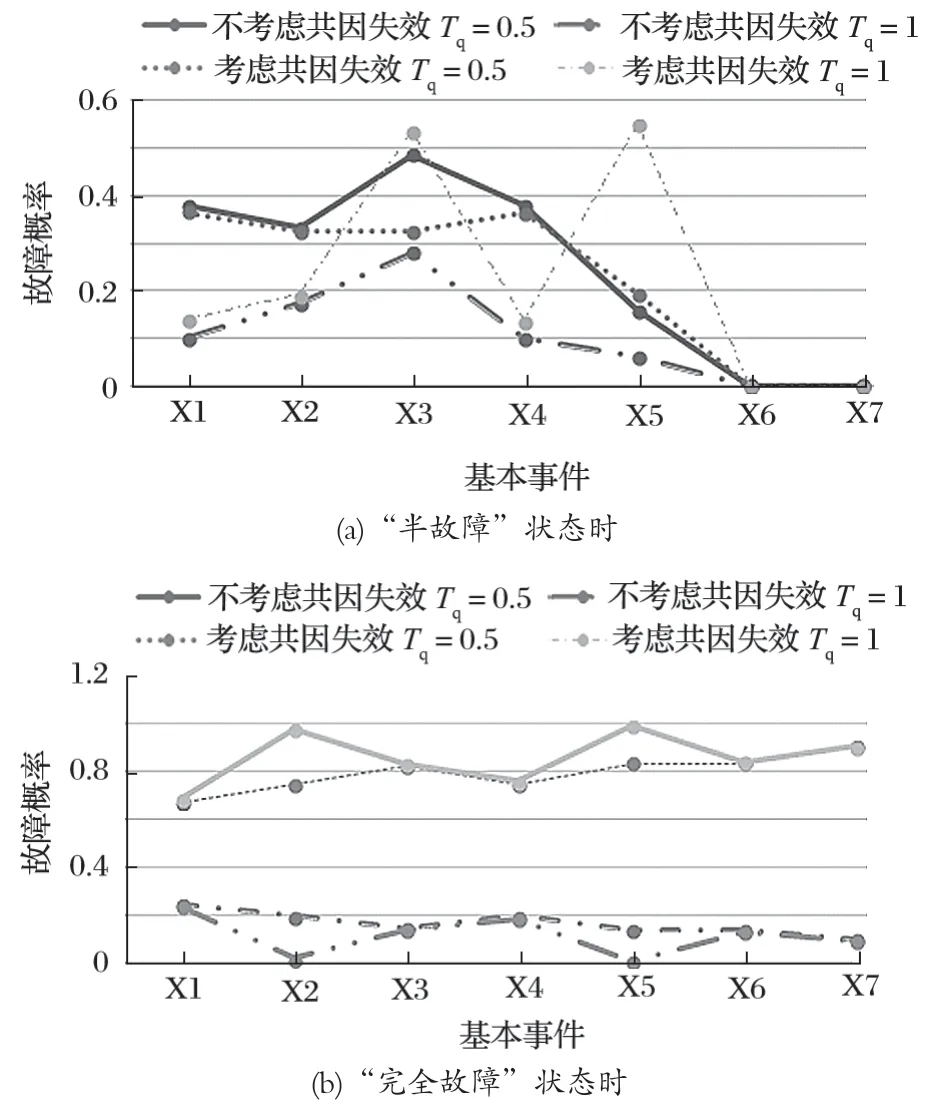
图5 根节点处于不同故障状态时顶事件故障概率对比Fig.5 Comparisonof failure probability of top event at various failure states of root node

由图 5 可知，当顶事件处于“完全故障”状态时考虑共因失效的各节点概率重要度比不考虑共因失效的各节点概率重要度有所增加，说明各节点故障对顶事件故障的影响增大。

4 结语

通过综合考虑矿井提升系统的模糊性、多态性及共因失效等因素，对现有故障树及贝叶斯网络分析方法进行了改进。

(1)利用三角模糊数表示零部件的模糊先验概率，在贝叶斯网络中修改条件概率表和各故障状态先验概率来反映多态性，运用β-因子和模型求解共因失效概率。

(2)将模糊、多态及共因失效等定性因素定量化，通过 Netica 软件能计算系统故障的概率值，为故障诊断提供基础；同时，通过对贝叶斯网络各根节点的重要度分析，能有效快速地找到对系统影响较大的零部件。

贝叶斯网络具有双向推理能力，可以对矿井提升制动系统进行可靠性评估以及故障诊断，通过后验概率和重要度的大小来发现系统中相对而言比较容易出现故障的环节，并根据实际情况制定相应的解决措施。该研究成果思路和具体方法也可以推广到其他机械系统特别是重大技术装备系统的可靠性研究中。

笔者研究虽然考虑了故障概率的模糊性以及各基本事件故障状态的多态性，但这些都是基于静态可靠性分析，未考虑系统的动态性和各零部件故障状态的时序性变化。因此，在后续的矿井提升制动系统分析中，可对其进行动态贝叶斯网络分析。