极薄煤层采煤机滚筒的装煤过程与性能评价

2020-03-24刘春生于念君张艳军

黑龙江科技大学学报 2020年1期

刘春生，于念君，张艳军

(1.黑龙江科技大学，哈尔滨 150022； 2.黑龙江科技大学机械工程学院，哈尔滨 150022)

0 引言

随着我国煤炭行业的发展，薄煤层的开采力度越来越大，特别是极薄煤层的开采。极薄煤层煤质优良，在我国储备较为丰富，但相比于中厚煤层，极薄煤层存在装煤效果较差。在影响装煤效果上，除采煤机自身结构外，在不同环境下滚筒工作参数的匹配也至关重要,国内外学者从数值模拟、理论和实验三方面对薄煤层装煤进行了诸多研究。如徐婵等[1]基于PFC3D仿真软件确定了螺旋滚筒叶片升角、滚筒转速、牵引速度最佳配比的关系。毛君等[2]采用EDEM离散元软件研究了某采煤机截深、转速与其装煤率、滚筒三向载荷、截割比能耗之间的相互关系。J.Rojek[3]采用离散元法建立了截齿与煤岩的切削过程。何景强等[4]指出螺旋滚筒破碎煤岩不是一个连续的过程。李晓豁等[5]根据前、后滚筒三向载荷和负载扭矩曲线及统计结果,揭示了采煤机截割载荷的大小、变化规律及其相关关系。赵丽娟等[6]分析了滚筒转速、牵引速度、叶片升角和截深对装煤效果的影响。刘春生等[7]通过分析颗粒对叶片作用力推导出了按轴向速度积分的装煤能力计算公式。张亮华[8]得出在逆转和顺转两个工况下变升角和叶片之间的作用关系，利用仿真进行了验证。邬黔凤[9]优化了截割比能耗和载荷波动系数，减小了滚筒在采煤过程中的波动。M.Ayhan[10]得出锥形筒毂比圆柱形筒毂的滚筒装煤效率更高。张亮华[10]指出在逆转和顺转两个工况下变升角和叶片之间的作用关系。

国内外大多数学者考虑装煤过程多倾向于从滚筒自身结构的改变和参数优化来提高装煤效果，而极薄煤层采煤机滚筒工作参数的匹配对装煤效率和装煤能耗影响程度上仍需要做进一步研究。因此，笔者针对小滚筒极薄煤层采煤机滚筒工作参数设计均匀实验，运用EDEM离散元软件对采煤机截割过程进行数值模拟，研究不同滚筒工作参数下该采煤机的装煤效率和装煤能耗，根据数值模拟结果修正装煤效率理论模型。

1 滚筒装煤过程的模拟

1.1 离散元理论模型

离散元素法是将研究对象看成由若干个离散的单元组成。每一个单元都相互独立，球形颗粒代替材料，每一个颗粒都有相应的尺寸、质量和接触参数[11-12]。运用牛顿第二定律求出单元的运动参数，这样重复计算，实现目标运动情况的预测。

在离散元颗粒之间力—位移关系中，接触刚度计算的正确性极为重要，法向刚度和切向刚度合成接触刚度[13]。由Hertz接触理论可推导出颗粒之间作用力与位移的关系式为

式中：F——两个互相接触颗粒间的作用力；

E*——颗粒i和j之间的等效弹性模量；

R*——颗粒i和j等效接触半径；

ε——颗粒间重叠量；

d——颗粒间的相对位移。

1.2 煤壁参数设置与三维模型的建立

根据离散元理论将固体物料煤岩壁看作由离散颗粒组成。运用离散元仿真软件EDEM中的颗粒模板建立直径为12 mm，接触半径14 mm的圆球颗粒如图1所示。设置颗粒力学参数和接触参数见表1和2。选用EDEM软件中Herz Mindin with Bonding接触模型建立煤岩颗粒墙壁，如图2所示。

图2 煤岩墙壁

表1 煤岩力学参数

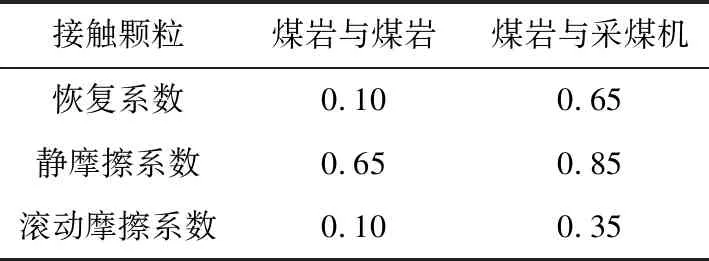
表2 颗粒运动系数

在实际煤矿中煤岩是连续体，在用颗粒组成煤岩墙壁时应考虑颗粒与颗粒之间的黏结参数，针对此次数值模拟实验设置颗粒与颗粒之间的法向刚度1.121 65×108N/m3，切向刚度9.732 0×107N/m3，法向最大应力8.318 3 MPa，切向最大应力2.357 3 MPa。

ProE软件绘制滚筒直径650 mm的极薄煤层采煤机以及刮板输送机的三维模型，将其保存为x-t格式文件，导入EDEM中,设置相关环境约束以达到和实际采煤相同的效果如图3所示。

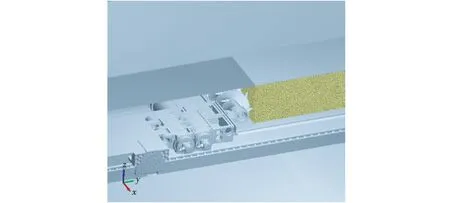
图3 数值模拟实验模型

1.3 滚筒工作参数与数值模拟方案

按照均匀设计方法，确定实验中主要因素(自变量)、各因素水平及相应因子(因变量)实验要考察的主要性能指标[14]。极薄煤层采煤机滚筒直径较小，其装煤能力与效果一直是影响采煤机工作性能的重要因素。为提高其工作性能，极薄煤层采煤机滚筒转速要高于中厚煤层采煤机滚筒转，因此,实验中自变量为牵引速度X1、滚筒转速X2,因变量为装煤效率η、装煤能耗ΔP。实验方案设计如下：在采煤角度0°下，牵引速度区间为2～6 m，滚筒转速区间为80～100 r/min。2个自变量的均匀设计表，见表3。共5组实验。

表3 2个自变量均匀设计

2 模拟过程与装煤效率

2.1 装煤过程模拟

该型采煤机滚筒直径为650 mm、宽度为700 mm，5组滚筒工作参数其装煤过程相似，因此，笔者随机选取实验5为例分析数值模拟过程，其煤岩颗粒运动过程如图4所示。

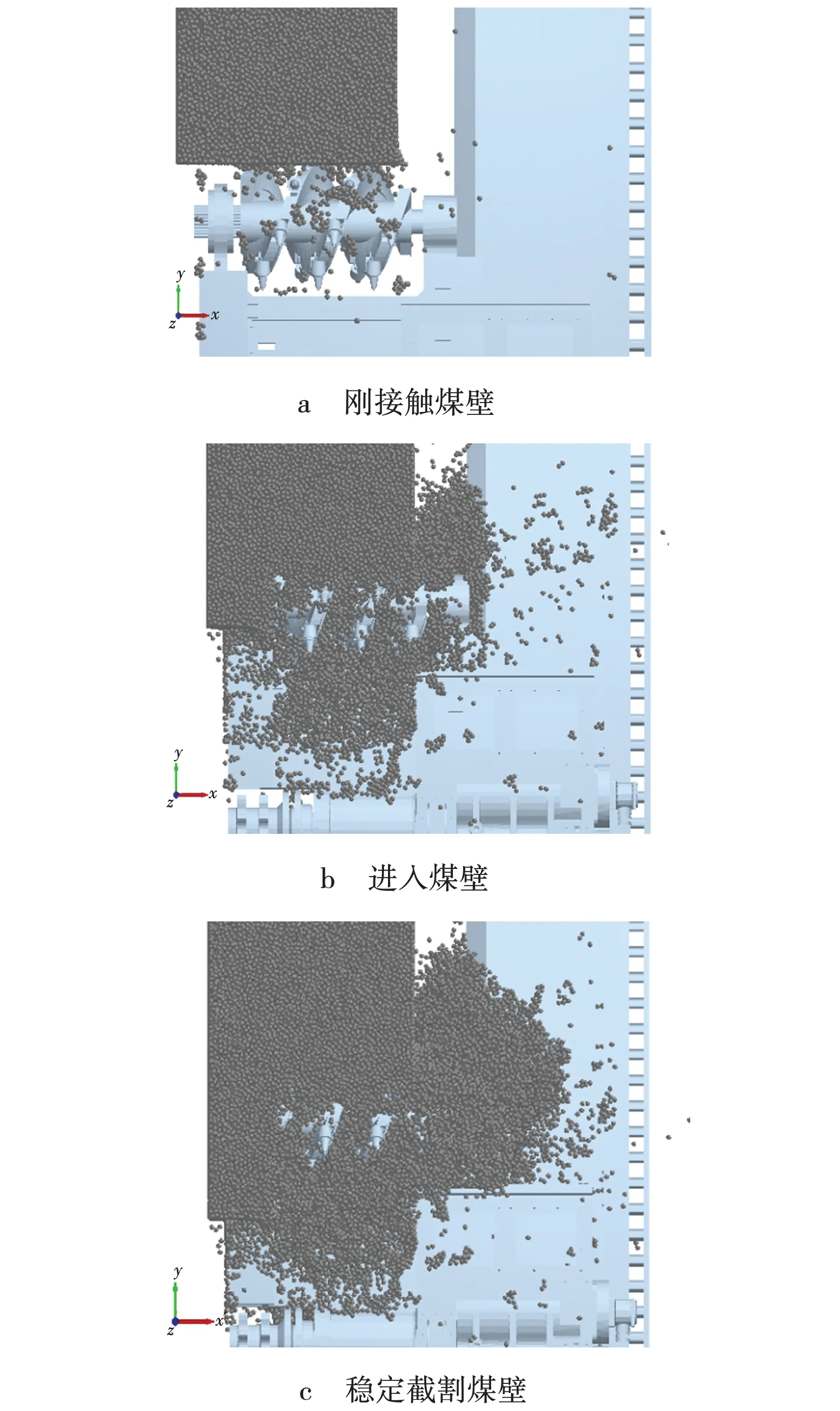
图4 滚筒连续截割煤岩

在滚筒刚接触煤壁时,由于螺旋滚筒抛射式采煤且滚筒转速较大，崩落下来的煤岩甩向滚筒后侧，随着滚筒深入截割，崩落下来的煤岩在螺旋叶片的作用下向刮板输送机方向推送，并在滚筒采空区侧的出煤口处形成煤岩堆积，当采煤机继续进给时在螺旋叶片的作用下堆积角逐渐增大，随着滚筒的转动和叶片的推动崩落下来的煤岩进入刮板输送机上。

随着采煤机进给，滚筒截落下的煤岩颗粒进入滚筒的螺旋叶片中。滚筒叶片区域内的颗粒速度云图与三向平均速度波动情况如图5、6所示。

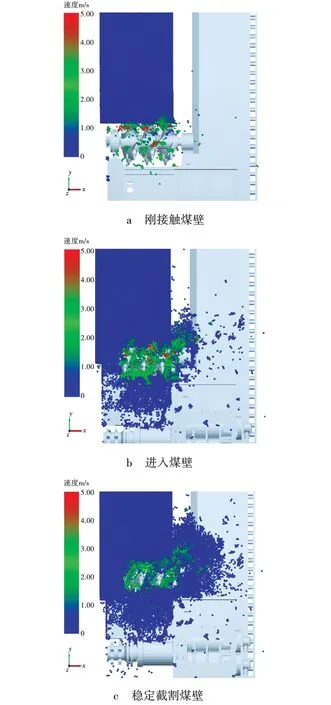
图5 滚筒区域内颗粒速度变化云图

由图6可见，滚筒刚接触煤壁时颗粒向滚筒后上侧抛射，因此在0至1 s时颗粒平均速度会在y方向(采煤机进给方向)会呈现出较大的负值，在z方向(机身高度方向)呈现较大的正值，在x方向(滚筒轴线方向)无明显规律。在1至2 s时由于截齿和叶片已切入煤壁，煤岩颗粒在叶片的作用下向刮板输送机所在方向运动，因此x正方向的颗粒速度逐渐增大在4 s时逐渐稳定。而y和z方向的速度也逐渐减小，在6～8 s时颗粒三向速度趋于动态稳定。

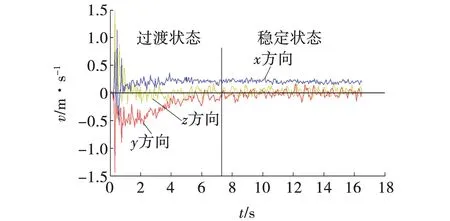
图6 滚筒区域内颗粒平均速度

2.2 装煤效率

2.2.1 数值模拟的装煤效率

运用EDEM后处理功能将该采煤机与煤岩位置划分区,如图7所示。以实验5为例，统计区域1的颗粒累积质量mz1变化趋势和区域2的颗粒累积质量mz2变化趋势如图8所示。a表示区域1单位时间颗粒质量，b表示区域2单位时间颗粒质量，c表示区域1累积颗粒总质量，d表示区域2单位时间累积颗粒总质量。

结合5组实验的数值模拟结果,统计区域1和2在稳定截割时煤岩颗粒残留质量，得出数值模拟装煤效率

式中：m1——区域1的颗粒质量；

m2——区域2的颗粒质量。

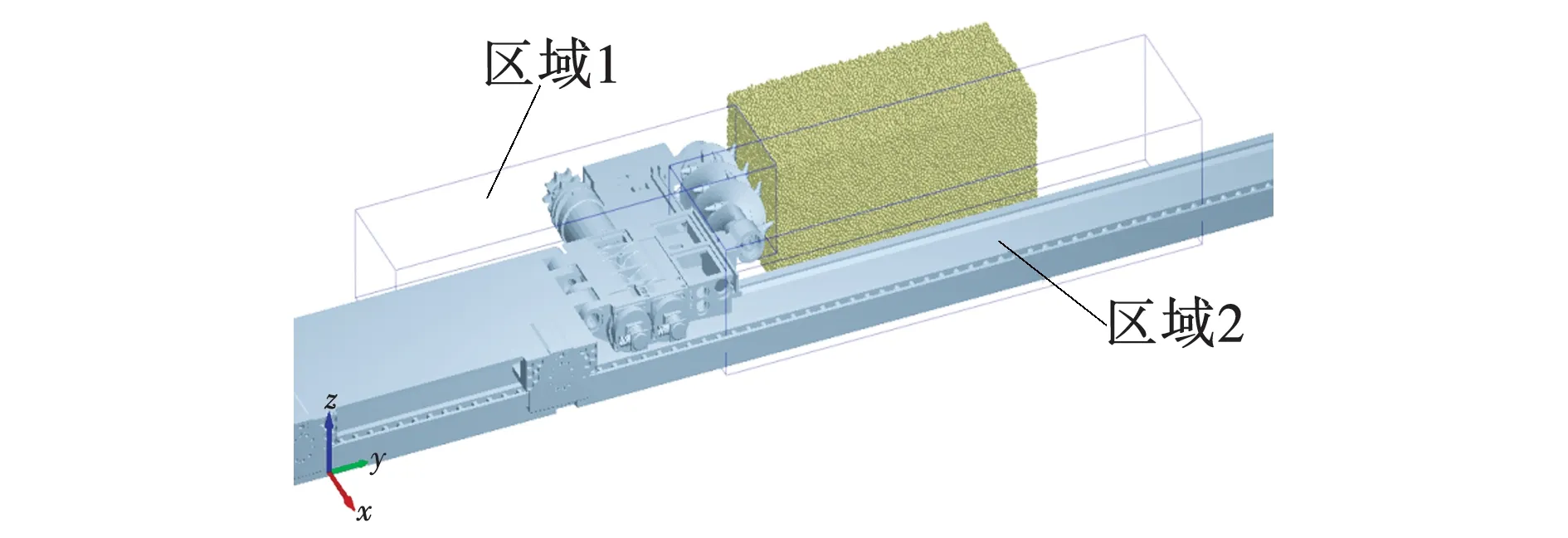
图7 采煤机区域划分

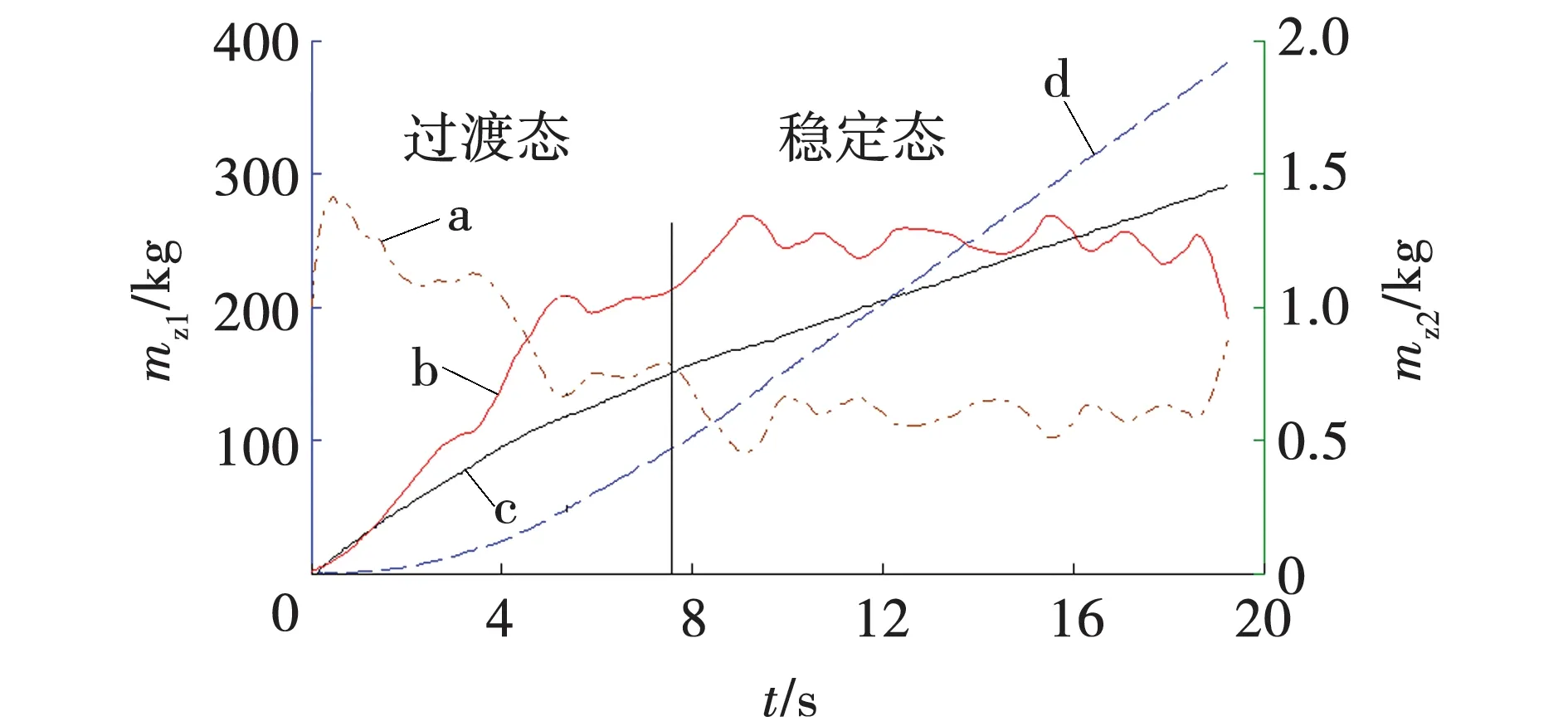
图8 颗粒质量与时间变化关系

由图8可见,在采煤机开始工作时，区域1的颗粒累积总质量增加，而区域2的颗粒累积总质量几乎为零。这是由于在开始工作时截齿和煤岩壁接触，叶片没有和煤岩壁接触。随着牵引推进，截割下来的煤岩颗粒没有进入螺旋叶片中，而是向后抛射，因此在0～2 s时区域1的颗粒累积总质量增加显著。随着滚筒进给，当叶片进入煤岩后，截割下来的煤岩颗粒在螺旋叶片的作用下进入区域2，区域1单位时间颗粒增加质量减小，区域2单位时间颗粒增加质量增大。当滚筒处于截割稳定状态后；在6～8 s时，区域2与区域1的单位时间颗粒增加的质量逐渐处于动态稳定。统计5组实验数值模拟结果，见表4。

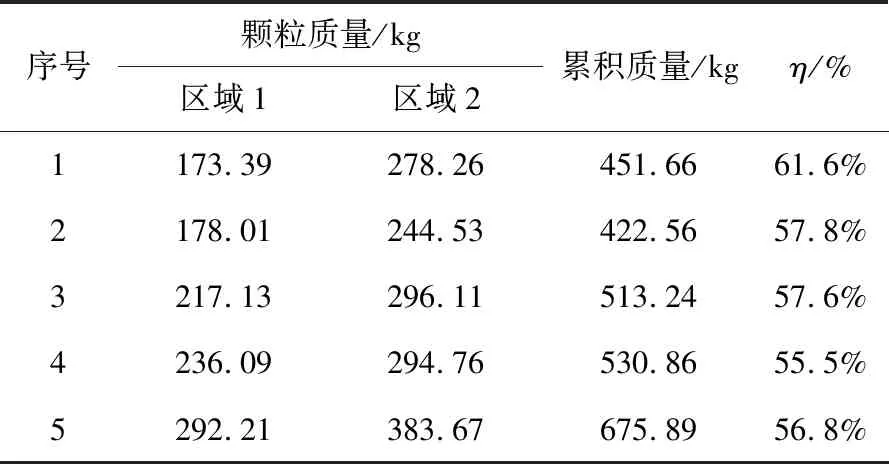
表4 数值模拟实验装煤结果

2.2.2 装煤效率综合模型

由理论分析可知，装煤效率为滚筒装煤能力与落煤能力的比值，其滚筒落煤能力为

Qt=Jvq[Dcλ-(Dc-Dy)]，

(1)

式中：J——截深，m；

vq——牵引速度，m/min；

Dc——滚筒直径，m；

Dy——叶片直径，m；

λ——煤岩体的松散系数，λ=1.5～1.7。

滚筒装煤能力

(2)

式中：n——螺旋滚筒转速，r/min；

S——螺旋叶片导程，m；

Dg——轮毂直径，m。

根据式(1)(2)比值计算其理论装煤效率

整理得

对于小直径滚筒，在采煤机实际工作时，随着滚筒转速增大，循环煤增大，装煤效率与滚筒转速呈非线关系即装煤效率减小[15]；由于装煤能力与装煤效率实验难度较大，因此为了更准确从理论上反映出装煤效率的关系，采用理论模型和数值模拟截割相结合，给出综合装煤效率的关系式

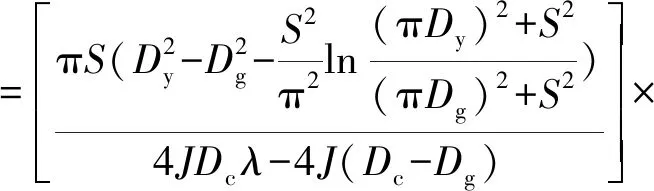
(3)

(4)

式中，k1、k2、k、ε——模型未知参数。

(5)

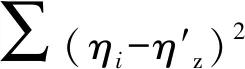
(6)

(7)

对式(6)(7)中的k1、k2与k、ε分别求偏导且令导数为0，即式(8)～(11)。

(8)

(9)

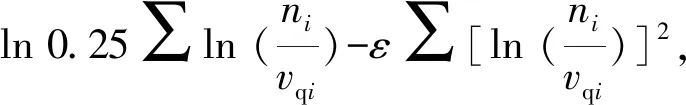
(10)

(11)

将上述数值模拟实验装煤效率ηi与滚筒参数ni，vqi代入式(8)～(11)求得修正系数k1、k2和k、ε即

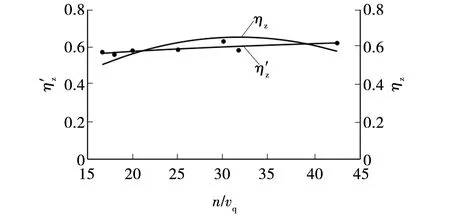
图9 修正模型对比

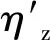
3 滚筒装煤的能耗

3.1 滚筒三向载荷

在不考虑叶片与煤岩之间摩擦时截割电机消耗总功率主要用于截煤和装煤。当截割功率不足时，会产生“闷车”致使生产效率降低，减少采煤机工作寿命，因此,在截割电机确定时分析其装煤功率与截割功率占比也是至关重要的。滚筒的装煤功率与截割功率主要由轴向载荷和截割载荷决定。以实验5为例,利用 EDEM 后处理功能，导出转速为100 r/min,牵引速度为6 m/min时滚筒三向载荷，如图10所示。

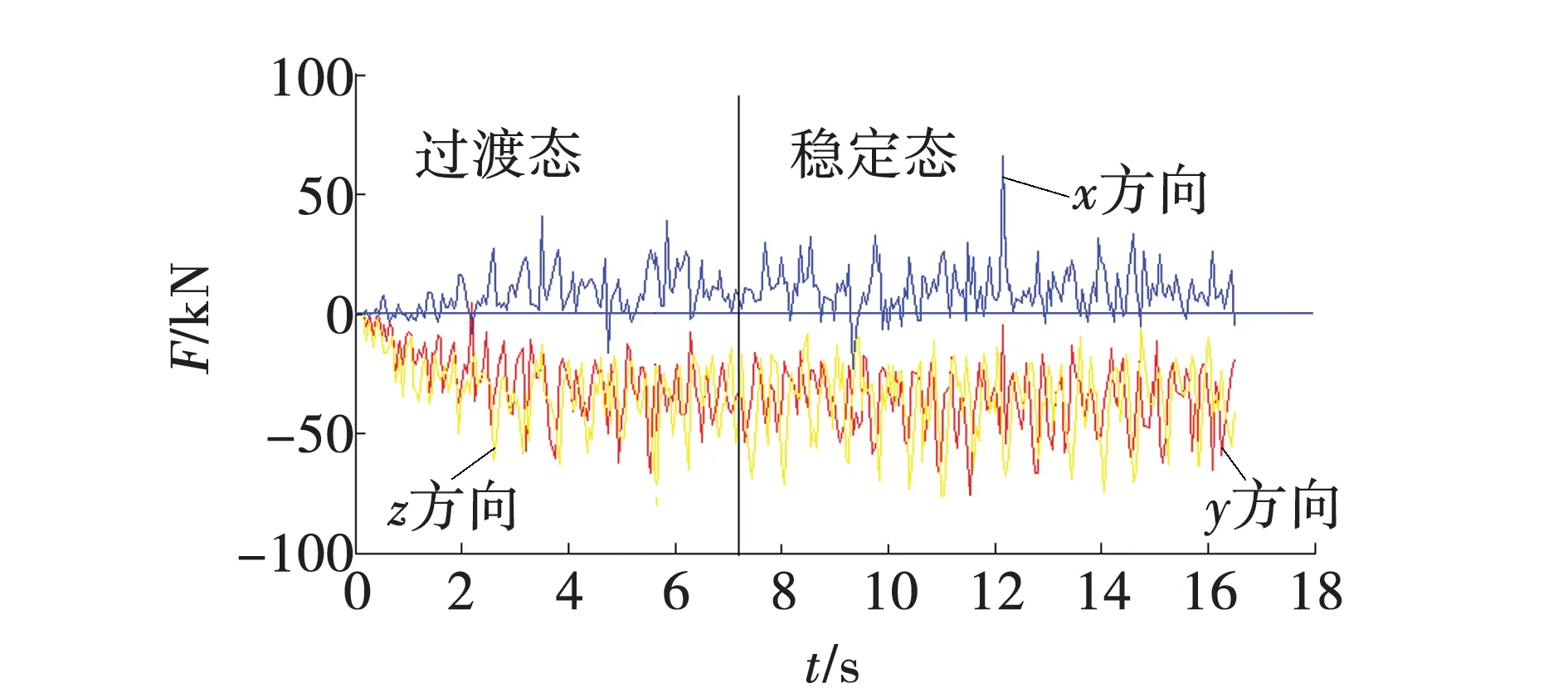
图10 滚筒三向载荷

由图10可见，y方向即滚筒进给载荷，z方向即滚筒截割载荷，在0～2 s内截齿接触煤岩随着采煤机的运动，截割载荷和进给载荷逐渐增大(滚筒所受进给载荷与截割载荷与EDEM系统坐标轴方向相反，进给载荷和截割载荷均为负值)，此时颗粒没有进入叶片区域内，轴线载荷变化不大，在2～4 s时颗粒逐渐进入螺旋叶片内轴向载荷增大，在6～8 s内滚筒载荷处于动态稳定。

3.2 滚筒截割载荷

运用EDEM提取5组数值模拟实验稳定状态下三向载荷绝对值与滚筒区域内颗粒的轴向平均速度，在不考虑颗粒与煤岩摩擦和循环煤情况下，根据式(12)计算滚筒稳定状态下装煤轴向等效功率，见表5。

P1=Fe(ve+fve)，

(12)

式中：P1——稳定状态滚筒装煤等效功率；

Fe——稳定状态滚筒轴向平均载荷；

ve——稳定状态滚筒区域内颗粒轴向平均速度；

f——颗粒与叶片摩擦系数，取0.25。

(13)

式中：P2——稳定状态滚筒平均截割功率；

M——稳定状态滚筒转矩；

ω——滚筒角速度。

M=FdR，

(14)

式中：Fd——稳定状态滚筒平均截割载荷；

R——滚筒半径。

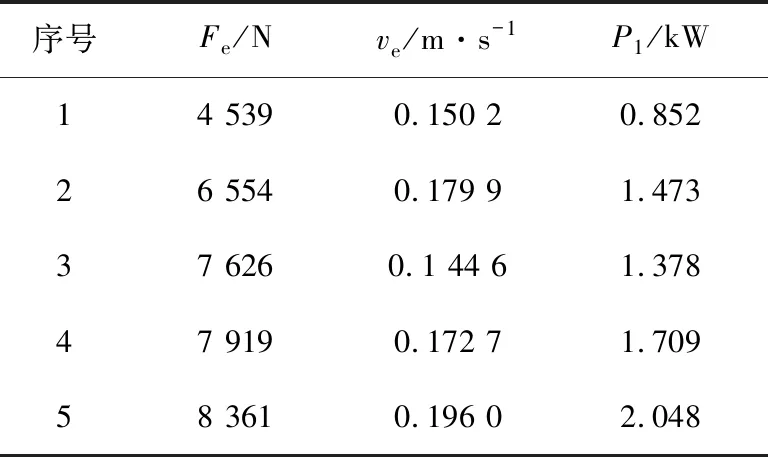
表5 装煤功率统计

根据式(13)计算滚筒截割功率，统计稳定区域内滚筒截割平均载荷，见表6。

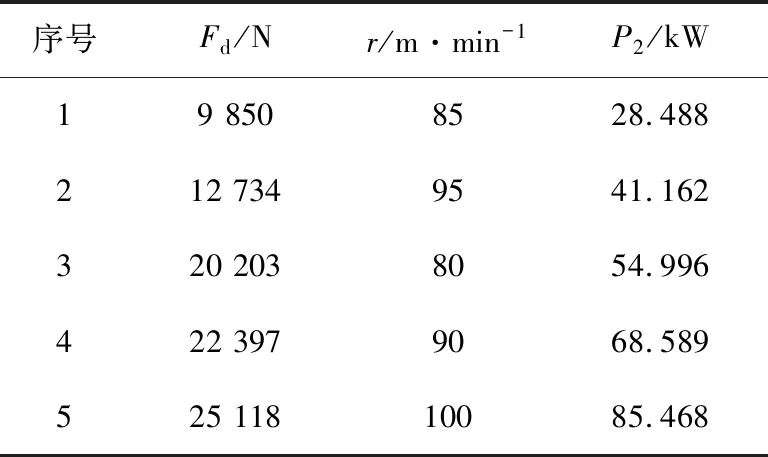
表6 截割功率统计

由表5、6可知，5组实验下的装煤功率和截割功率，根据式(15)计算各滚筒工作参数下的装煤功率与总功率的占比即装煤能耗，见表7。

(15)

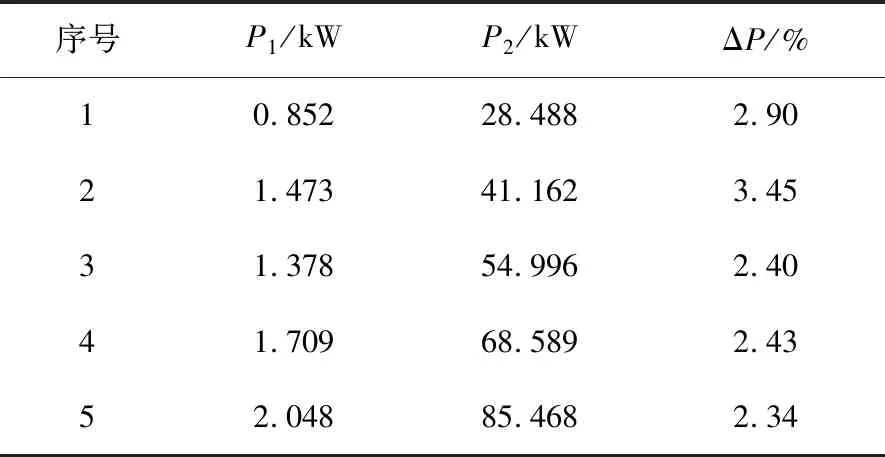
表7 装煤能耗统计

由表5、6可见，5组数值模拟实验下牵引速度变化对装煤轴向等效功率，截割载荷和截割功率影响大于滚筒转速对其影响，随着采煤机牵引速度增加，装煤轴向等效功率，截割载荷和截割功率呈现增大趋势，结合表7可见，随着牵引速度的增加单位时间内截割功率比装煤轴向等效功率增加速率快，因此其装煤能耗随牵引速度增加整体呈减小趋势。