针对缺失不平衡数据的自适应马氏距离双权重过采样方法研究
2020-03-24周迪豪
周迪豪,宋 燕
(上海理工大学 光电信息与计算机工程学院,上海 200093)
0 引言
分类问题是模式识别等众多计算机领域的一个重要分支。分类问题往往存在类别不平衡现象。在不平衡情况下,若又存在信息缺失现象,则分类器性能会受到巨大影响[1]。在现实世界中,由于受数据复杂性及测量设备局限性等影响,数据不平衡和数据缺失现象普遍存在。在二类不平衡数据集中,样本较少的类称为少类,样本较多的类称为多类,若直接对数据集进行分类,则少类样本容易被忽略,而多类样本会被过度关注,从而导致分类器向多类倾斜[2]。而少类样本通常包含有重要信息,例如在诊断样本中,少类样本的误分类可能会造成严重的危害[3]。因此,解决缺失数据的不平衡问题就显得尤为重要。
通常,处理不平衡类的方法主要有两种:基于模型(算法)方法和基于数据方法[4]。基于模型方法,如cost-sensitive boosting 算法[5]考虑了错误分类的代价,而非类与类之间的关系。然而,当发生类别分布重叠时,模型的性能可能会大大下降[6]。基于数据方法的主要目标,是利用采样技术调整样本数,从而达到类别平衡。采样方法大致可分为欠采样和过采样[7]。前者是删除多类中多余的样本,而后者则是为少类合成新样本。Tomek links[8]是最具代表性的欠采样算法,它可以消除在类边界附近的噪声样本。然而,由于样本的删除,欠采样可能导致数据集关键信息的丢失。相反,通过合成新的少类样本来平衡类别规模,过采样方法得以保留大部分数据集信息[3]。目前,人们在过采样方面已经做了大量的工作并体现在文献中。如SMOTE、ADASYN、Kmeans SMOTE 和MWMOTE[9]。SMOTE 针对少类合成新样本,但在边界处易产生错误样本,如图1(a)所示。

图1 SMOTE 与K-means SMOTE 合成策略示意图Fig.1 The schematic diagram of SMOTE and K-means SMOTE
ADASYN 在SMOTE 的基础上考虑加强了边界点权重,分类超平面更显著。K-means SMOTE 利用K 均值聚类形成簇,并分配簇权重以合成新样本,如图1(b)所示。图中的椭圆轮廓越粗代表该簇的权重分配得越大。MWMOTE 不仅考虑了少类信息,其将多类信息也纳入考量范围,并作为分配少类样本权重的依据。尽管上述方法考虑到了类别分布,但却没有充分考虑数据少类的类内分布。
另一方面,数据缺失又是不平衡数据分类中另一大困难,数据丢失可能会严重影响模型的性能,因此,在分类前对缺失值进行填补是非常重要的。目前,缺失值插补的代表性研究成果包括:回归插补(RI)、经验最大化(EM)、多重插补(MI)和k-NN 插补法[10]。此外,文献[11]提出一种基于非负潜在因子的矩阵分解(LMF)模型,用于填补缺失值的方法。该方法能够更好地利用样本的全局信息,改善了回填精度。文献[12]表明,传统过采样算法在回填缺失值后通常不能保证完全符合原始样本分布,而传统过采样方法的插值公式使得合成样本的不确定性进一步加大。对此,一种基于模糊的信息分解(FID)[13]被提出,该算法能够同时解决不平衡问题和信息缺失问题。然而,由于模糊隶属度的存在,FID 对局部信息的依赖程度很高,可能导致过拟合现象。因此,探究一种新的算法来有效地处理带有缺失值的不平衡数据集成为一个急需解决的问题。根据文献[14]的启发,马氏距离能够有效解决样本集中普遍存在特征量纲不一的问题。
本文根据上述难题,提出一种针对含有缺失信息的不平衡数据的自适应马氏距离多权重过采样方法(MAWOTE)。该方法首先通过基于MGBD 更新规则的NLFs 模型,将不完整的数据集填补完整,其次基于马氏距离将数据集中样本使用模糊C 均值聚类(FCM),随后对各样本簇自适应分配双权重,并根据k 近邻信息进行过采样,最后使用SVM,验证算法的有效性。
1 相关技术
1.1 马氏距离
本文所提出的过采样算法是依据马氏距离[14]。马氏距离在计算时考虑了数据集的相关关系,与欧氏距离不同的是它考虑到各种特性之间的联系。如图2 所示,在欧式距离中,A 点与B 点到原点的距离相同,然而在马氏距离中,A 点与B 点到原点的距离则不相同,因为马氏距离表示的是数据的协方差距离。

图2 欧式距离与马氏距离示意图Fig.2 Schematic diagram of Euclidean distance and Mahalanobis distance
假定样本向量x=(x1,x2,…,xn)T和y=(y1,y2,…,yn)T,两点间欧式距离为:

样本x到样本均值μ的马氏距离表示为:

在此,可以考虑一个协方差矩阵S,协方差计算如式(3)所示:

因此,马氏距离可以通过式(4)求解:

当协方差矩阵为单位矩阵时,马氏距离可等同于欧氏距离。
1.2 模糊C 均值聚类
FCM 算法在K-means 算法的基础上增加了模糊思想。不同于K-means 的硬聚类,FCM 提供了一个概率性的灵活簇划分结果。FCM 通过最小化目标函数将数据集划分为c个簇:

其中,xj(j=1,2,…,n)表示数据集{x1,x2,…,xj}中第j个样本;U≜{uij}(1=1,2,...,c;j=1,2...,n)为隶属度矩阵;元素uij代表样本xj的隶属度;参数m >1 表示模糊因子。
基于式(5),ci和uij的更新公式为:

FCM 聚类算法交替更新聚类中心ci和隶属度矩阵U,直至收敛或迭代次数达到设定值。
2 缺失值填补及过采样方法
为了使缺失的数据能够得到精确填补,并使过采样后新生成的样本即可靠又重要,本文使用小批量梯度下降法求解NLFs 后,在马氏距离度量的基础上,对少类样本簇使用自适应的双权重分配策略进行过采样,最终得到一个平衡数据集。基于此,本文提出一种针对缺失不平衡数据的自适应马氏距离双权重过采样方法(MAWOTE)。
2.1 非负矩阵分解插补方法
为了在解决缺失值现象的同时,避免过拟合现象。根据非负矩阵分解(NMF)模型[11],假设存在一个含有n个样本m个特征的数据集矩阵Rn×m,则定义存在3 个矩阵能够构成Rn×m,即NLFs 模型:
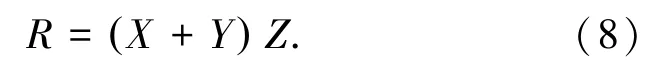
与文献[11]相似,根据上式可构造用以最小化的损失函数:

式中,ri,j、xi,k、yi,k和zk,j分别对应R、X、Y和Z中的项,d为潜在因子数。为了避免过度拟合,在模型中考虑了正则化项,λX、λY、λZ是非负正则化系数。第三矩阵使得模型拥有了更多的解空间,以此可得到更好的精度[16]。
通常情况下,批梯度下降(BGD)算法,是解决最小化问题时运用最广泛的更新规则之一[17]。然而,由于每次迭代都需要使用所有样本来寻求最优解,会造成很大的计算开销。因此,在BGD 的基础上,随机梯度下降法(SGD)[18]被提出。SGD 每次迭代时只更新一个样本,以加快训练速度。然而,SGD可能导致算法收敛于局部最优。相比之下,小批量梯度下降(MBGD)算法[19]中和了BGD 算法和SGD算法的优点,即每次训练时从所有样本中随机选择一定数量的样本用以更新。基于MBGD 的更新规则,矩阵X、Y和Z的更新规则可用式(10)-式(12)表示:

考虑到在更新过程中学习率可能为负,为了保证样本矩阵的非负性,因此设置:

上述公式提供了基于MBGD 的NLFs 更新规则。通过MGBD 更新迭代后,所有缺失值将通过NLFs 填补,并得到与原始数据集相似的信息,有助于后续过采样时对分布信息的利用。
2.2 样本聚类
传统的随机插值过采样生成新样本的方法,容易导致错误样本的产生。即该类样本位于多类样本中,从而导致新的噪声点产生。MAWOTE 基于马氏距离,采用FCM 算法对少类样本以及多类样本分别进行聚类,在簇中过采样可保证新样本的可靠性。聚类后形成的少类样本簇可以定义为S,多类样本簇可以定义为L。则二者的簇样本数量可分别表示为,将少类簇及多类簇的簇中心分别表示为
2.3 自适应分配权重
为了在对少类簇过采样时充分考虑每个簇内部的数据分布和簇间的差异,提出了一种双权重分配方法来确定每个少类簇应当生成新的少类样本的数量。在马氏距离度量基础上,双权重要素包括:类簇间距离要素和簇稀疏度要素。
类簇间距离为首要因素,它衡量了不同簇到分类边界的远近从而判断其对分类的重要性,通过下式计算:

表示第i个少类簇中心以及第j个多类簇中心。由于越靠近边界的样本信息在分类中越重要,且不易学习。因此,当第i个簇距离多类样本越远时,类间距离因子ri变小。
另一因素是少类簇的稀疏度,其可以描述少类簇中样本的密度分布情况,如式(20):

其中mi表示第i个少类簇的样本数,xil表示第i个少类簇第l个样本。由此可见,当第i个少类簇分布得越紧密时,pi越大。
考虑到上述两个因素,确定每个少类簇需要合成的新样本数,用以下公式对距离因素和密度因素进行归一化:

其中,Rmax为max{ri};Rmin为min{ri};Pmax为max{pi};Pmin为min{pi};i=1,2,...,。
综合上述因素,考虑边界点信息与簇密度信息,自适应双权重分配因子可表示为:

最后,若给定G 作为MAWOTE 需要在少类中新合成的总样本数,则其中第i个少类样本簇需要合成的样本数量gi可以通过下式求得:

2.4 过采样插值
有别于传统的欧式距离过采样方法,MAWOTE算法在过采样时使用马氏距离作为度量标准,该方法能够消除特征间量纲不一问题。此外,为了减少随机采样中产生的不确定性,MAWOTE 算法引入k近邻概念,保证了过采样后的数据集服从原始数据分布。因此,基于马氏距离,从第i 个少类簇中随机抽取样本Ni,s,并通过下式过采样新样本:

式中,θi为一个[0,1]之间的随机数;ki为预先给定的最近邻参数;Ni,sj为ki个最近邻样本的其中之一。在后面的实验中,为了计算简单,在少类簇中不同ki被定义为相同的,即ki=k。需要注意的是,上述公式中距离计算公式皆使用马氏距离。
为了更清晰地展示MAWOTE 算法,其具体步骤如下:
(1)输入含有缺失值的不平衡数据集;
(2)运用NLFs 模型以及MBGD 更新规则,对数据集中的缺失值进行填补;
(3)针对填补后完整的数据集,基于马氏距离,分别对少类与多类样本聚类;
(4)自适应计算每个少类样本簇对应分配的权重;
(5)对少类进行过采样,合成新的少类样本以平衡数据集。
3 实验结果与分析
3.1 数据集与评价标准
为了验证本文算法的有效性和适用性,实验从UCI 机器学习库[20]中选取了6 个公共数据集,以此来研究MAWOTE 在各种场景下的性能。表1 为本文中使用的数据集信息。
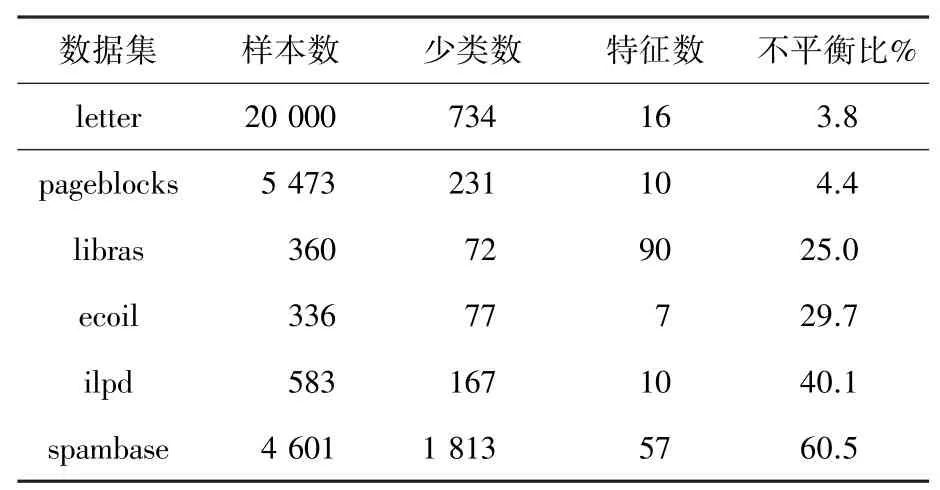
表1 UCI 数据集信息表Tab.1 Information of the UCI Datasets
本文以不同的比率{0.1,0.3,0.5},随机删除特征值。通过不同大小、属性和不平衡比率的数据集,验证MAWOTE 算法的泛化性能。
对于应用过采样算法的分类器性能,根据文献[13],引入4 个主要的评价指标,其中包括总体准确度、查准率、查全率和G-Mean:


OverallAccuracy(ACC)反映了正确分类的样本数量。然而,在不平衡学习条件下,ACC 无法准确判断少数样本的分类情况。式中TP 和FN,分别表示少类中正确预测和错误预测的样本数,TN 和FP分别表示多类中正确预测和错误预测的样本数。
此外,在数据不平衡的情况下,ROC 曲线下面积(AUC)是一个评估分类器性能的重要指标。因此,AUC 指标也将被纳入衡量指标中。AUC 越接近1,分类性能越好。
3.2 对比实验分析
本文所有实验都是在一台2.2 GHz CPU、16 GB内存、Ubuntu 操作系统的电脑上完成,软件环境为python3.7。
为了验证本文算法的优越性,选用支持向量机(SVM)作为基本分类器,在{1,10,100}范围内,对松弛变量进行优化。为了验证所提出的算法与传统方法相比是否能达到有效水平,本文对比了各种过采样及缺失值填补方法,见表2。参数设置参考文献[13]。

表2 对比实验方法表Tab.2 Methods for Comparative Experiments
在MAWOTE 算法中,为了方便计算,设置λX=λY=λZ=1。FCM 中模糊因子m根据经验值通常取2[15],ki从{3,5,8,10}中根据性能表现选取最优值。
结合上述评价指标,表3 和表4 展示了两种缺失率状态下的算法最佳性能,其中粗体字代表该组中最佳结果。
表3 及表4 的实验结果表明,在大缺失、大规模的不平衡数据集下,MAWOTE 的性能波动更小。尽管MAWOTE 并不在所有数据集中最优,但其拥有更好的泛化性能。FID 是MAWOTE 着重对比的算法,FID 的“查准率”指标明显大于“查全率”指标,这说明分类超平面仍然倾斜。而MAWOTE 在马氏距离的基础上考虑了更多的样本类内信息,因此在面对不同数据集时,性能稳定性更具优势。
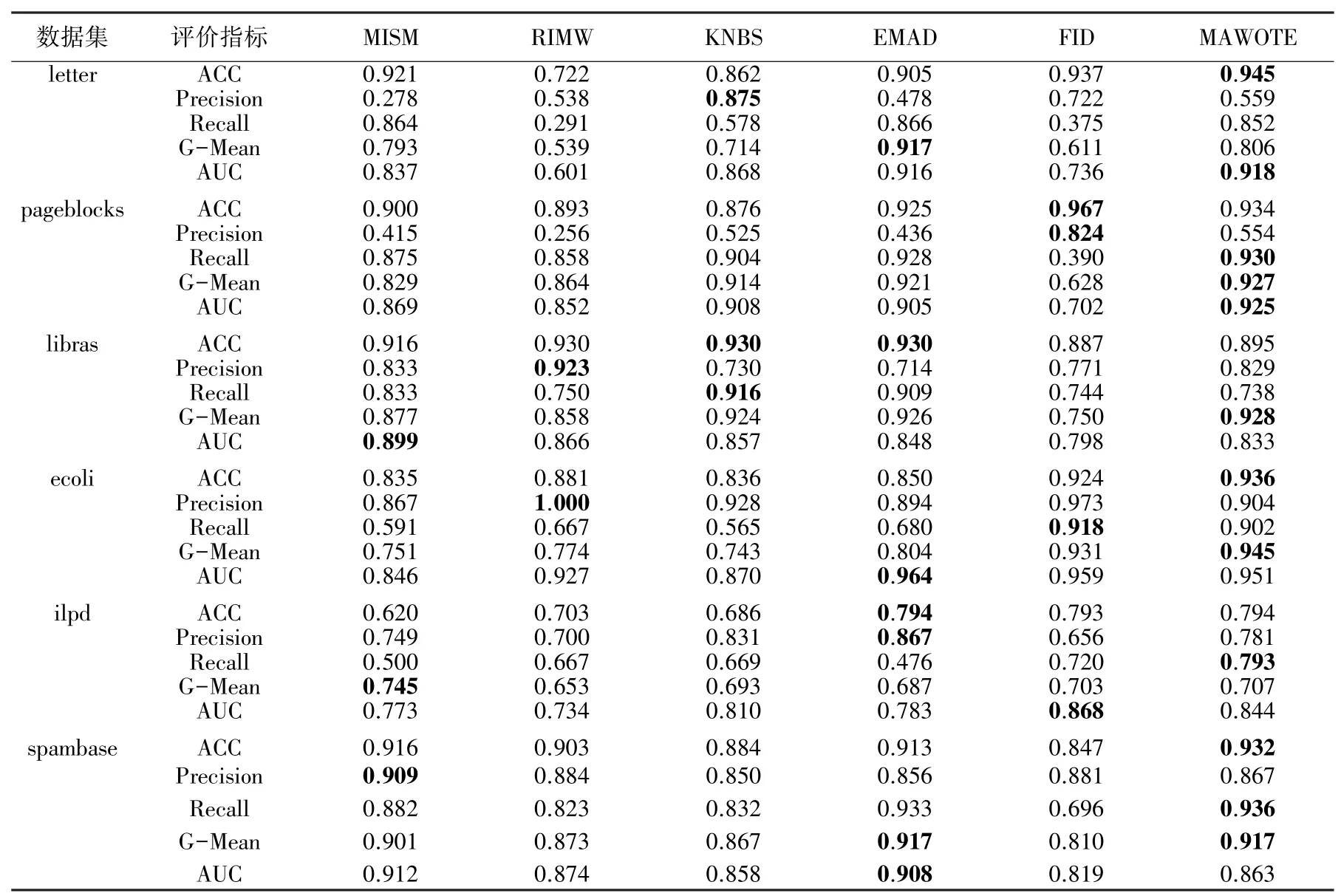
表3 0.1 缺失率下的比较结果表Tab.3 Comparison results on 0.1 missing rate

表4 0.5 缺失率下的比较结果表Tab.4 Comparison results on 0.5 missing rate
4 结束语
本文提出了一种针对含带缺失信息的不平衡数据的自适应马氏距离双权重过采样方法,即MAWOTE 算法。MAWOTE 的基本思想概括为:考虑样本中全局已知特征值的信息,利用扩展了解空间后的NLFs 模型,结合MGBD 更新规则,对数据集进行精确的填补;引入了马氏距离消除特征间的量纲不一问题;在使用FCM 算法生成类别簇的基础上,综合类间距离、类内密度因素,对少类簇自适应分配双权重,提高合成样本质量;采用k 近邻思想在少类簇内合成新的少类样本,保证数据集在新样本添加后,依然能够维持原始信息分布。实验结果表明,MAWOTE 在6个不同大小、维度、缺失率的数据集上取得了稳定的性能表现,与过往的算法相比,性能更为突出。
