从高观点视域下扩展分析一道高中物理题

李博 王庆勇 侯恕

摘 要：阿特伍德机是高中物理典型的理想化模型，也是牛顿第二定律应用的典型实例.本文基于大学物理中质点运动学及刚体力学的知识，从“两类十种”视角，解析“理想型”与“半理想型”阿特伍德机的物理规律.通过扩展分析一道典型的高中物理习题，引导中学物理教师要适时从高观点的视域下看待高中物理知识及物理教学.

关键词：阿特伍德机;高中物理习题;十种解题方法

文章编号：1008-4134（2020）05-0059中图分类号：G633.7文献标识码：B

基金项目：吉林省高等教育教学改革重点项目“基于‘问题-实践-反思教学模式的微格实践教学体系的构建与改革研究”，2019;吉林省高等教育教学改革研究重点项目“高校通识教育改革的实践研究——以D大学文科物理课程为个案”，2015.

作者简介：李博（1996-），男，黑龙江哈尔滨人，硕士研究生，研究方向：物理课程与教学论;

王庆勇（1978-），男，山东嘉祥人，博士，讲师，研究方向：非线性量子可积问题;

侯恕（1965-），女，吉林九台人，博士，副教授，研究方向：物理课程与教学论.

本文从大学物理中质点运动学及刚体力学的视角，运用“两类十种”分析方法，全面地解析阿特伍德机这一物理模型，能为解决此类问题提供一套比较系统的物理分析思路.

1 经典试题

例题 如图1，一根细绳跨过轻而无摩擦的滑轮，在绳的两端悬挂质量分别为M=2kg和m=1kg的物体，滑轮系在由天花板垂下的链子OA上.试求：当两物体匀加速运动时：

（1）细绳的拉力T;（2）链子OA的拉力F.（g取10m/s2）

【常规解答】

（1）选取竖直向下为正方向，根据牛顿第二定律

对M分析，有 Mg-T1=Ma1

对m分析，有 mg-T2=-ma2

由题意可知，忽略滑轮转动及系统的摩擦，则有

a1=a2=a，T1=T2=T

解得：a=M-mM+mg=13g，T=2MmM+mg=43mg=403N

（2）对链子OA进行分析，根据物体的平衡有

F-2T=0

解得 F=2T=803N

分析：本题是高中物理力学部分牛顿第二定律的典型应用实例，难易程度属于中等.选定参考系及规定正方向后，通过对系统中的两物块进行受力分析，可以列出其动力学方程，并根据题意，可忽略滑轮的转动、绳子的质量及系统的摩擦.本题能较好地让学生初步理解并应用牛顿第二定律，同时也能初步掌握 “轻绳”“轻质滑轮”这两种理想化模型.

2 试题原型——阿特伍德机

例题中嵌套了一种典型的高中物理模型——阿特伍德机，所谓阿特伍德机，就是将两质量分别为M、m的物体系于一条跨过定滑轮轻质软绳的两端，这样就组成了阿特伍德机[1]，如图2所示.

若两物体的质量满足M>m，将两物体由静止释放，那么质量为M的物体竖直向下运动，质量为m的物体竖直向上运动，两物体的加速度大小均为a，定滑轮沿逆时针旋转.

阿特伍德机是英国剑桥大学阿特伍德为验证牛顿第二定律所设计的一个滑轮装置，是可以验证较多牛顿力学定理的典型模型之一[2].阿特伍德机之所以重要，不仅是因为其在高中物理力学体系中具有基础性、典型性等特点，还因为其在科学研究中可以验证许多牛顿力学定律，例如牛顿第二定律、动量定理、确定重力加速度等[3].

3 “两类十种”解题方法

3.1 第一类：“理想型”阿特伍德机的分析

“理想型”阿特伍德机，即忽略滑轮的转动、绳子的质量及系统的摩擦.

在这种物理情境中，以地面为参考系，两物体的速度关系为v=v1=-v2，加速度关系为a=a1=-a2，绳的张力关系为T=T1=T2.

【视角1】从牛顿第二定律角度分析（如图3）.

定理 F外=mdv→dt=ma→.

分析：选取竖直向下为正方向，对M分析，有

Mg-T=Ma

对m分析，有 mg-T=-ma

解得 a=M-mM+mg T=2MmM+mg

【視角2】从质点运动学角度分析（如图4）.

定理 v→=dx→dt=x→·，a→=dv→dt=d2x→dt2=v→·=x→··.

分析：以定滑轮圆心为零点，选取竖直向下为正方向，并设绳长为l.

对M分析，有 Mg→+T=Ma→1

对m分析，有 mg→+T=ma→2

绳长为固定值，则有 x1+x2+πR=l

两侧对时间求二阶导数，有 x··1+x··2=0，即

a→1+a→2=0

解得 a→1=M-mM+mg→，a→2=m-MM+mg→，T=-2MmM+mg→

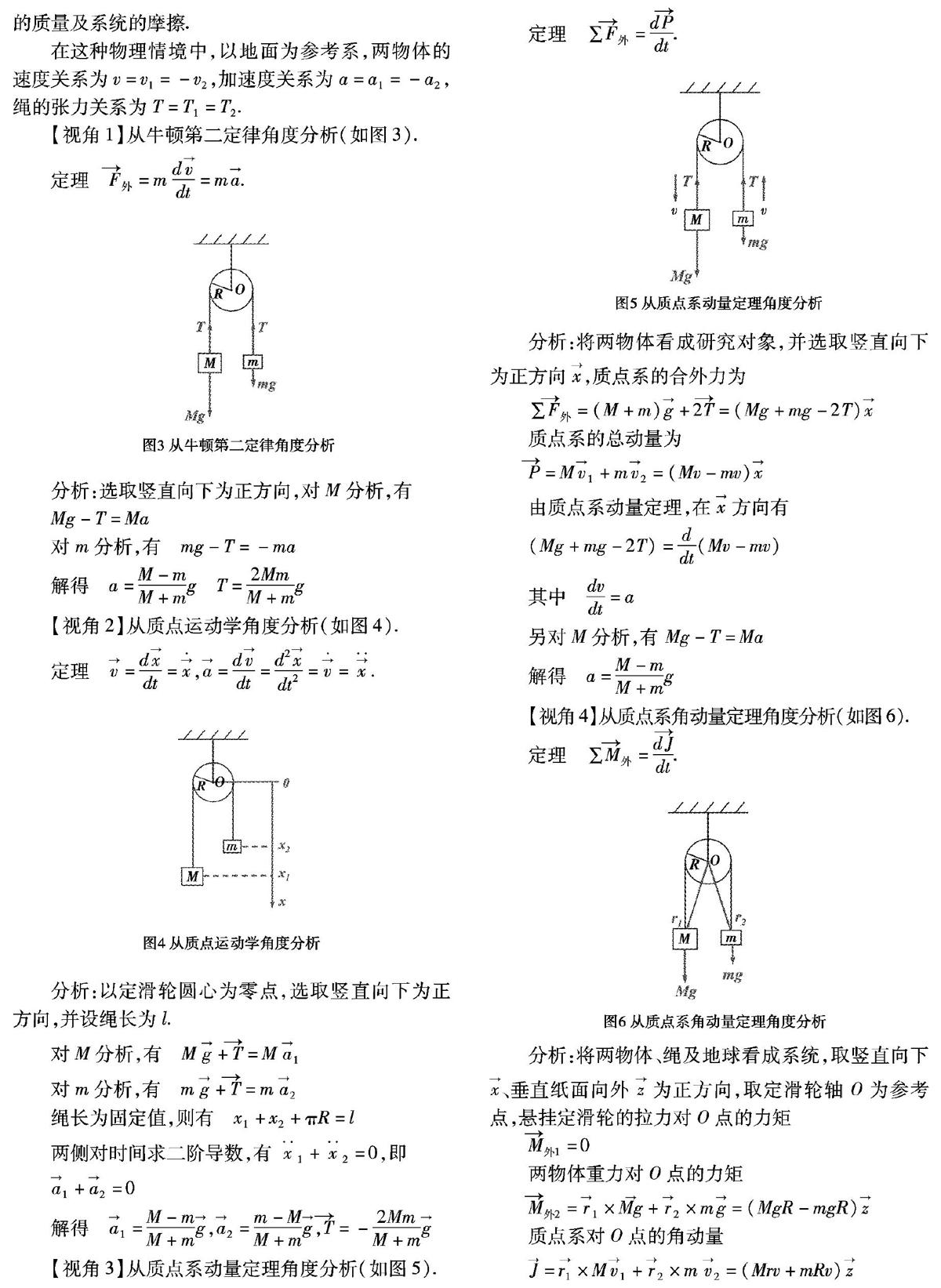
【视角3】从质点系动量定理角度分析（如图5）.

定理 ∑F外=dPdt.

分析：将两物体看成研究对象，并选取竖直向下为正方向x→，质点系的合外力为

∑F外=（M+m）g→+2T=（Mg+mg-2T）x→

质点系的总动量为

P=Mv→1+mv→2=（Mv-mv）x→

由质点系动量定理，在x→方向有

（Mg+mg-2T）=ddt（Mv-mv）

其中 dvdt=a

另对M分析，有 Mg-T=Ma

解得 a=M-mM+mg

【视角4】从质点系角动量定理角度分析（如图6）.

定理 ∑M外=dJdt.

分析：将两物体、绳及地球看成系统，取竖直向下x→、垂直纸面向外z→为正方向，取定滑轮轴O为参考点，悬挂定滑轮的拉力对O点的力矩

M外1=0

两物体重力对O点的力矩

M外2=r→1×Mg→+r→2×mg→=（MgR-mgR）z→

质点系对O点的角动量

J→=r1→×Mv→1+r→2×mv→2=（Mrv+mRv）z→

由质点系角动量定理，有

（MgR-mgR）=ddt（MRv+mRv）

其中，dvdt=a

解得 a=M-mM+mg

【视角5】从质点系动能定理角度分析（如图7）.

定理 dEk=∑δA内+∑δA外（微分形式），Ek2-Ek1=∑A内+∑A外（积分形式）.

分析：系统所受外力仅为重力，对两物体的元功为dA外=Mgdh+mg（-dh）

将两物体看成一组质点系，其动能的增量为dEk=d[12（M+m）v2]

由质点系动能定理，得

Mgdh-mgdh=d[12（M+m）v2]

两侧对时间进行求导，得

Mgdhdt-mgdhdt=ddt[12（M+m）v2]

其中 dhdt=v dvdt=a

解得 a=M-mM+mg

【视角6】从质点系机械能守恒定律角度分析（如图8）.

定理 对于保守系，dAD外=0，d（Ek+Ep）=0，Ek+Ep=常量E.

分析：将两物体、绳及地球看成系统，重力则为保守内力，并取地面为零势能面，质点系的动能为

Ek=12（M+m）v2

质点系的势能为 Ep=Mgh1+mgh2

由质点系机械能守恒定律，得

12（M+m）v2+（Mgh1+mgh2）=C

两侧对时间求导，得

（M+m）vdvdt+（Mgdh1dt+mgdh2dt）=0

其中 -dh1dt=dh2dt=v，dvdt=a.

解得 a=M-mM+mg

3.2 第二类：“半理想型”阿特伍德机的分析

“半理想型”阿特伍德机，即只考虑滑轮的转动，忽略绳子的质量及系统的摩擦.

在这种物理情境中，系统中的物体便不能仅被看成可以忽略转动及其形状、大小的“质点”模型了，还应考虑定滑轮本身的转动对于系统的影响，即将定滑轮看成形状和大小完全不变的物体——质量为M′的刚体.以地面为参考系，两物体的速度关系为v=v1=v2，加速度关系为a=a1=-a2，绳的张力关系为T1≠T2.

【视角1】从牛顿第二定律+刚体定轴转动定理角度分析（如图9）.

定理 ∑F外=mdv→dt=ma→，∑M外∥=dJ∥dt=Iβ→.

分析：取竖直向下、垂直纸面向外为正方向，

对M分析，有 Mg-T1=Ma

对m分析，有 mg-T2=-ma

对定滑轮分析，有 ∑M外=∑（r→×F）=（T1R-T2R）z→=Iβz→

其中，定滑轮的转动惯量I=12M′R2，

a=dvdt=d（ωR）dt=Rdωdt=Rβ

解得 T1=（M′+4m）MgM′+2（M+m），T2=（M′+4M）mgM′+2（M+m），

a=2（M-m）M′+2（M+m）g.

【视角2】从质点系角动量定理+刚体定轴转动定理角度分析（如圖10）.

定理 M外=dJdt，J刚∥=Iω→.

分析：将两物体、绳、定滑轮及地球看成系统，取竖直向下、垂直纸面向外为正方向，取定滑轮轴心O为参考点，

悬挂定滑轮的拉力对O点的力矩M外1=0

两物体重力对O点的力矩

M外2=r→1×Mg→+r→2×mg→=（MgR-mgR）z→

滑轮重力对O点的力矩M外3=0

质点系对O点的角动量J→=r→1×Mv→1+r→2×mv→2+Iω→=（MRv+mRv+Iω）z→

由质点系角动量定理，在z→方向有

（MgR-mgR）=ddt（MRv+mRv+Iω）

其中，dvdt=a，dωdt=β，v=ωR，I=12M′R2

解得 a=2（M-m）M′+2（M+m）g

【视角3】从质点系动能定理+刚体平面平行运动角度分析（如图11）.

定理 dEk=∑δA内+∑δA外（微分形式），Ek刚=12Iω2.

分析：系统所受外力仅为重力，对两物体的元功为dA外=Mgdh+mg（-dh）.

将两物体及定滑轮看成一组质点系，其动能的增量为

dEk=d[12（M+m）v2+12Iω2]

由质点系动能定理，得

Mgdh-mgdh=d[12（M+m）v2+12Iω2]

其中，ω=vR

代入，得 Mgdh-mgdh=d[12（M+m+IR2）v2]

两侧对时间进行求导，得

Mgdhdt-mgdhdt=ddt[12（M+m+IR2）v2]

其中，dhdt=v，dvdt=a，I=12M′R2

解得 a=2（M-m）M′+2（M+m）g

【视角4】从质点系机械能守恒定律+刚体平面平行运动角度分析（如图12）.

定理 对于保守系，d（Ek+Ep）=0，Ek+Ep=常量E，Ek刚=12Iω2.

分析：将两物体、绳、定滑轮及地球看成系统，重力则为保守内力，并取地面为零势能面.

质点系的动能为 Ek=12（M+m）v2+12Iω2

质点系的势能为 Ep=Mgh1+mgh2+M′gh

由质点系机械能守恒定律，得

[12（M+m）v2+12Iω2]+（Mgh1+mgh2+M′gh）=C

其中，ω=vR.代入，得

12（M+m+IR2）v2+（Mgh1+mgh2+M′gh）=C

两侧对时间求导，得

（M+m+IR2）vdvdt+（Mgdh1dt+mgdh2dt）=0

其中，-dh1dt=dh2dt=v，dvdt=a，I=12M′R2.

解得 a=2（M-m）M′+2（M+m）g

4 结束语

本文主要以阿特伍德机为研究对象，从“两类十种”视角分析了“理想型”与“半理想型”阿特伍德机的物理规律，在高观点的视域下归纳总结了阿特伍德机的各种计算方法.

总结来讲，对于中学物理教师，不能将物理“知识”变为“知识点”，不能仅拘泥于一道高中物理题，要尝试从大学物理的站位和角度来指导中学物理教学.

参考文献：

[1]梁瑾静，谢晓妹. 一种验证动量定理的新方法[J]. 实验教学与仪器，2018（08）：32-33.

[2]陳钢，晏世雷. 质点系中阿特伍德机对有关定理的检验意义[J]. 物理与工程，2013，23（04）：14-15.

[3]王学军. 阿特伍德机[J]. 物理实验，1988，8（02）：93-97.

[4]邱国民，叶玉琴. 一道选择题的解法赏析[J]. 物理通报，2011（09）：78-79.

[5]赵凯华，罗蔚茵. 新概念物理教程力学（第二版）[M]. 北京：高等教育出版社，2012.

（收稿日期：2019-12-03）