内爆作用下RC框架结构SAP数值模拟

2020-03-23孙欣欣冯锦飞田志昌

工程爆破 2020年1期

李娟，孙欣欣，冯锦飞，田志昌

(内蒙古科技大学土木工程学院，内蒙古包头 014010)

近年来，由燃气、化学品爆炸引起的建筑物内部爆炸事件频频发生。内爆作用下RC框架结构可能产生局部破坏甚至会发生连续性倒塌，造成经济和人身安全等方面的巨大损失[1-2]。因此RC框架结构的抗爆设计应当引起足够的重视，而基于用爆炸试验的结构设计，成本高且安全性差。因此很多学者采用LS-DYNA等精度较高的大型有限元软件对内爆作用下的RC框架结构进行数值模拟。但这类软件一般多为复杂工程计算以及科研所用，其前后处理较复杂，运算时间长，对硬件要求较高，不适用于计算较大的结构模型。而且使用这类软件模拟爆炸过程对设计者的理论知识基础要求较高，需掌握空气动力学、流固耦合等方面的理论。一般建筑结构设计人员很难在短时间内熟练掌握这类软件并将其应用于结构分析设计。所以，很多学者采用简单的拆除构件法来研究爆炸荷载作用下RC框架结构的抗连续倒塌性能[3]，但是只考虑关键构件失效对结构的影响，没有切合实际地考虑爆炸冲击荷载对爆源附近其他构件的直接作用。为此，选择前后处理较为简便、易于操作的SAP2000作为分析工具，提出了一种在通过构件拆除法实现关键构件失效的同时，考虑爆炸荷载对爆源附近其他构件直接作用的简便且接近实际的分析方法，使建筑结构设计人员能在短时间内高效、正确地完成内爆作用下RC框架结构的建模、分析和设计工作。

1 爆炸荷载模型

1)超压峰值Δp。对于爆炸冲击波峰值超压的具体函数形式，已有很多国内外研究人员进行了大量的试验，并提出了很多经验公式。通过对比各经验公式得到的爆炸冲击波峰值超压Δp对比距离z的曲线[4-5]，结合所涉及的对比距离，并考虑到峰值超压的不确定性，选取峰值超压偏大的公式作为基本峰值超压值的表达式。结合文献[6]与萨多夫斯基公式，得出Δp的表达式如下：

(1)

式中：Δp为爆炸冲击波峰值超压，MPa；z为对比距离，m/kg1/3。

依据文献[7]的《爆炸基本原理》，刚性地面爆炸与自由空气中爆炸的对比距离存在如下关系:

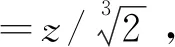
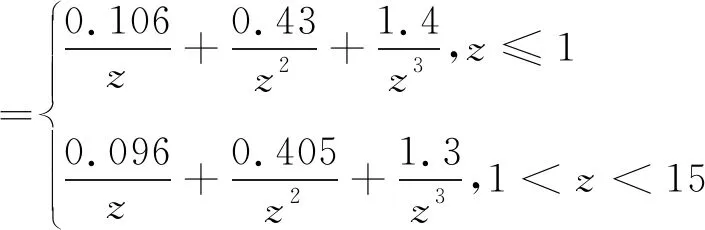
(2)

张传爱[8]通过对室内爆炸冲击波进行数值模拟，与在自由空气场的爆炸冲击波峰值超压经验公式比较，发现其Δp可扩大2倍，且冲击波第1次反射后到达目标结构的值与初次作用在该结构的值相等，综合考虑这些因素，将式(2)扩大3倍，即：

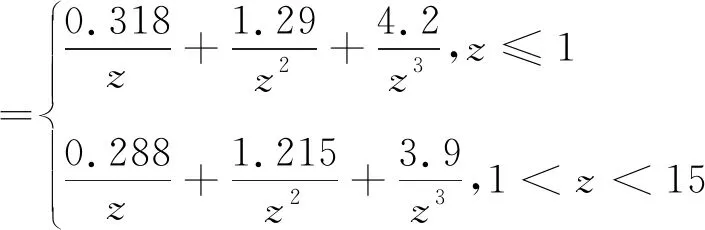
(3)

2)正压区作用时间。关于爆炸冲击波正压区作用时间的经验公式有很多。考虑到对比距离以及各经验公式的差别较大，为安全考虑选取Baum公式[8]:

(4)

式中:t+为正压区作用时间，s；W为TNT炸药的当量质量，kg;i为比冲量值，N·s/m2；A为系数，取值20～25之间；R为距离，m。

张传爱研究发现相比空气中爆炸的比冲量值，室内(地面)爆炸时比冲量值增长为7倍[9]，即：

(5)

即：

(6)

3)爆炸冲击荷载模型。爆炸冲击荷载模型即作用到结构上的冲击压力与作用时间的关系，由于其方程式过于复杂以及参数的不易确定性，国内外研究者将冲量相等的原则引入了爆炸荷载的简化模型。因此研究爆炸冲击荷载直接作用于结构的情况，可选用简化模型(见图1)。

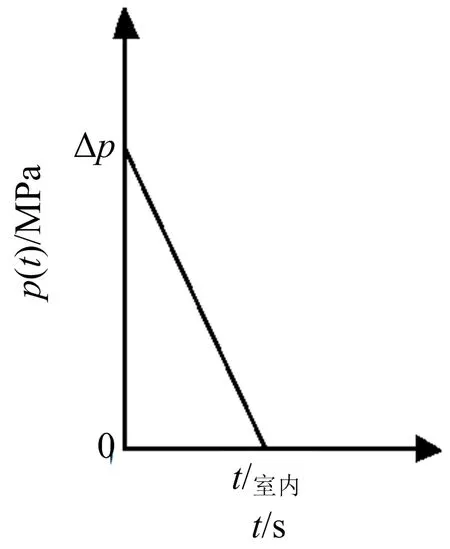
图1 简化模型Fig.1 Simplified model

其表达式如下：

(7)

2 SAP2000有限元模型

1)模型概况。采用的模型为一个8层的RC框架结构。模型中结构的抗震设防烈度为8度，框架抗震等级为3级。结构总高36.6 m，首层层高5.1 m，2～8层层高4.5 m，柱间距均为6 m。1～2层柱截面尺寸为600 mm×600 mm，3～5层柱截面尺寸为550 mm×550 mm，6～8层柱截面尺寸为500 mm×500 mm；框架梁截面尺寸均为300 mm×600 mm；标准层楼板厚120 mm，顶层楼板厚130 mm。梁、柱混凝土等级均为C35，板混凝土等级C30。梁、柱内的受力钢筋为HRB400级钢筋，板内受力钢筋为HRB335级钢筋。结构模型平面布置如图2所示。

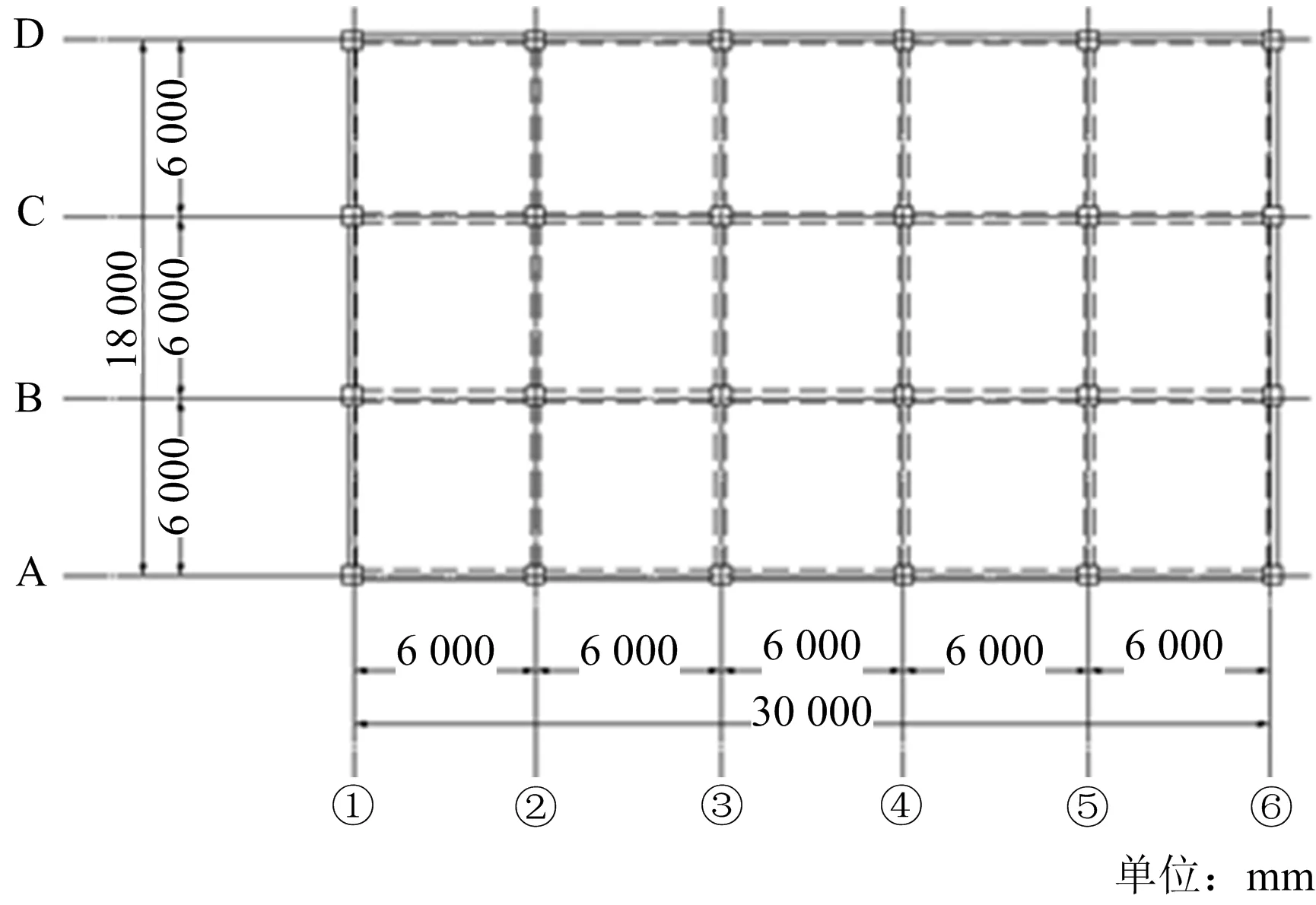
注：①～⑥表示横向轴线编号；A～D表示纵向轴线编号图2 结构平面布置Fig.2 Structure layout

2)荷载值、作用位置、分析时间。静力荷载值包括楼面恒荷载5.0 kN/m2、活荷载2.0 kN/m2；屋面恒荷载7.5 kN/m2、活荷载0.5 kN/m2，内墙自重荷载5.7 kN/m，外墙自重荷载8 kN/m2。动力荷载值选取5 kg TNT炸药量，爆炸点位于B轴和④轴相交处的底层403号内柱。选取梁柱节点进行分析，节点编号如图3所示。

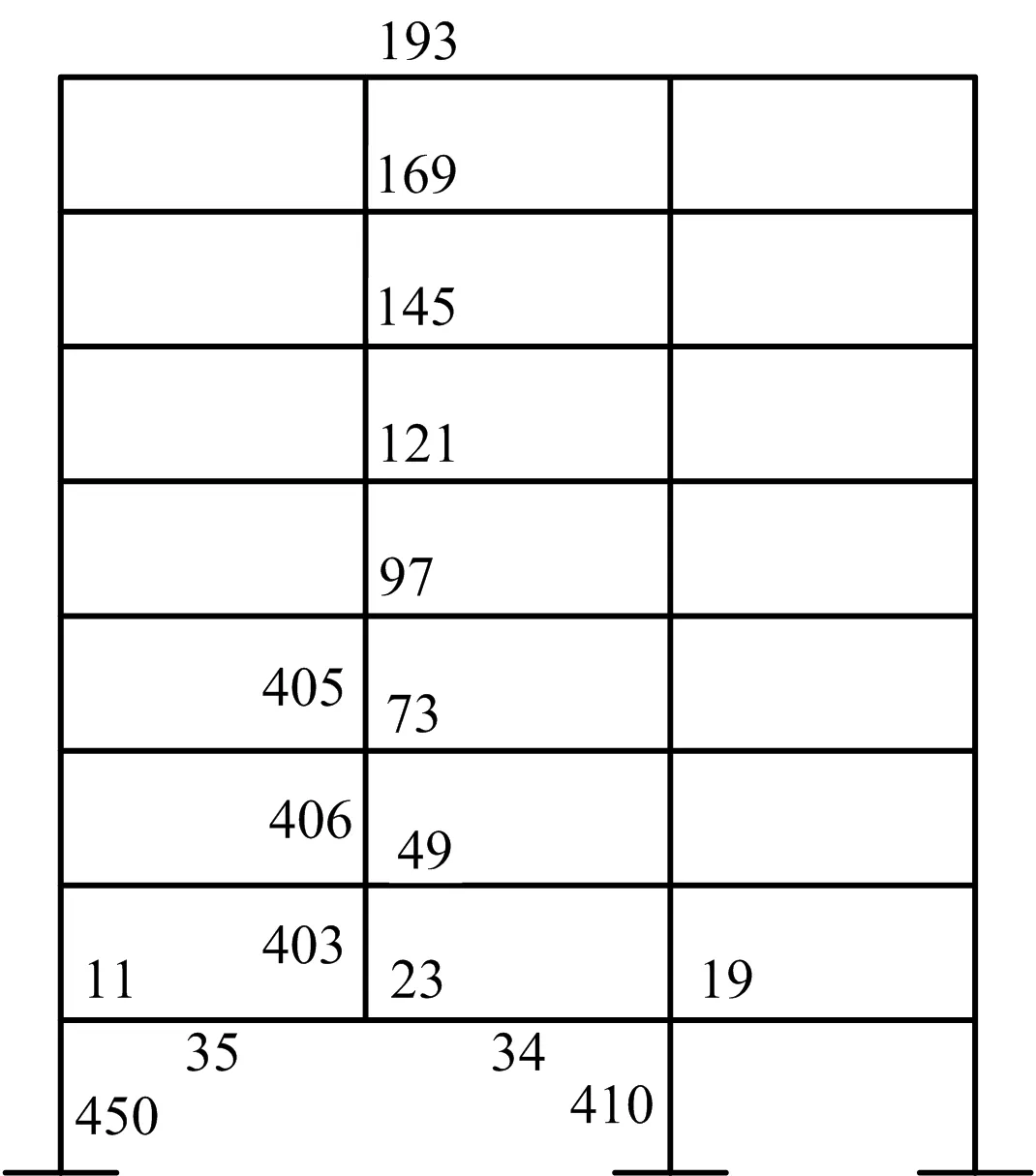
图3 梁柱节点编号Fig.3 Beam-column node number

对于爆炸冲击荷载作用下结构动力响应的数值计算方法采用SAP2000默认的HHT法。考虑到结构自振周期在2～3 s，那么0.1 T的范围就在0.2～0.3 s，为了更准确的得到结果，定义分析时间步长的大小为5×10-3s，分析600步，即总的分析时间为3 s。

3)有限元建模。梁、柱采用Solid164实体单元，楼板采用分层壳单元，边界条件为下端固定，建立三维有限元结构模型如图4所示。

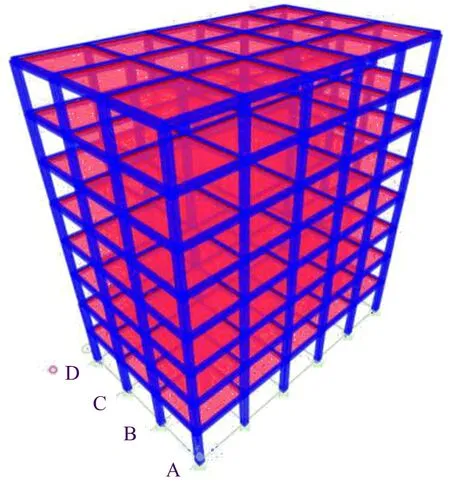
图4 RC框架结构模型Fig.4 RC frame structure model

通过结构构件截面发生转动表示发生塑性变形，所以，定义弯矩为M3(在所有梁的两端和梁中间位置处)、压弯铰(耦合铰)为P-M2-M3(在所有柱子的端部位置处)、弯矩铰为M2-M3(在所有柱子中间位置处)。

3 SAP2000的非线性分析

1)拆除关键柱后的结构静力非线性分析。在模型中施加恒荷载和活荷载，在达到静力平衡后计算出关键柱与梁相连的柱端轴力p(见图5)。拆除关键柱，用反力p代替原有关键柱的作用，使得到的模型与原结构静力等效，并将此工况设定为非线性静力分析工况。

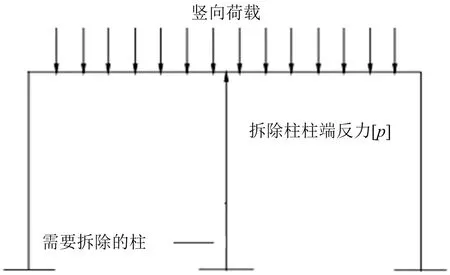
图5 柱子拆除前结构静力状态Fig.5 Static state of the structure before the column is removed

2)阻尼分析。在结构的动力分析中，结构的能量耗散是通过阻尼实现的，进行数值分析时，多数方法亦是通过在分析中加入合适的人工阻尼或数值阻尼来获得较为稳定的解。故在模拟分析中，采用Rayleigh阻尼，运行模态分析确定出动力分析工况有较大影响的高阶振型，并以此振型频率确定出非线性动力分析的阻尼参数，Rayleigh阻尼假设阻尼与质量矩阵和刚度矩阵的组合成比例，即

C=a0M+a1K

(8)

等号俩边同时除以2Mω，得出阻尼比与频率的关系为

(9)

式中：C为阻尼矩阵；M为质量矩阵；K为刚度矩阵；a0、a1为比例常数；ω为频率；ξ为阻尼比。

令ξm=ξn=0.05，ωm取多自由度体系的基频，ωn取对结构动力反应有明显影响的高阶振型，可通过非线性静力分析得到。由此确定出比例常数a0、a1的值，并以此算出结构阻尼矩阵。

3)施加爆炸荷载后结构动力非线性分析。依据确定的爆炸冲击荷载简化模型计算出动力荷载p(t)，将其施加在与p同样位置的响应构件上，并对拆除关健柱周围的梁、板施加动力荷载(见图6)。该工况以第1步非线性静力分析工况的终点为起点，并以此开始进行结构动力非线性分析。

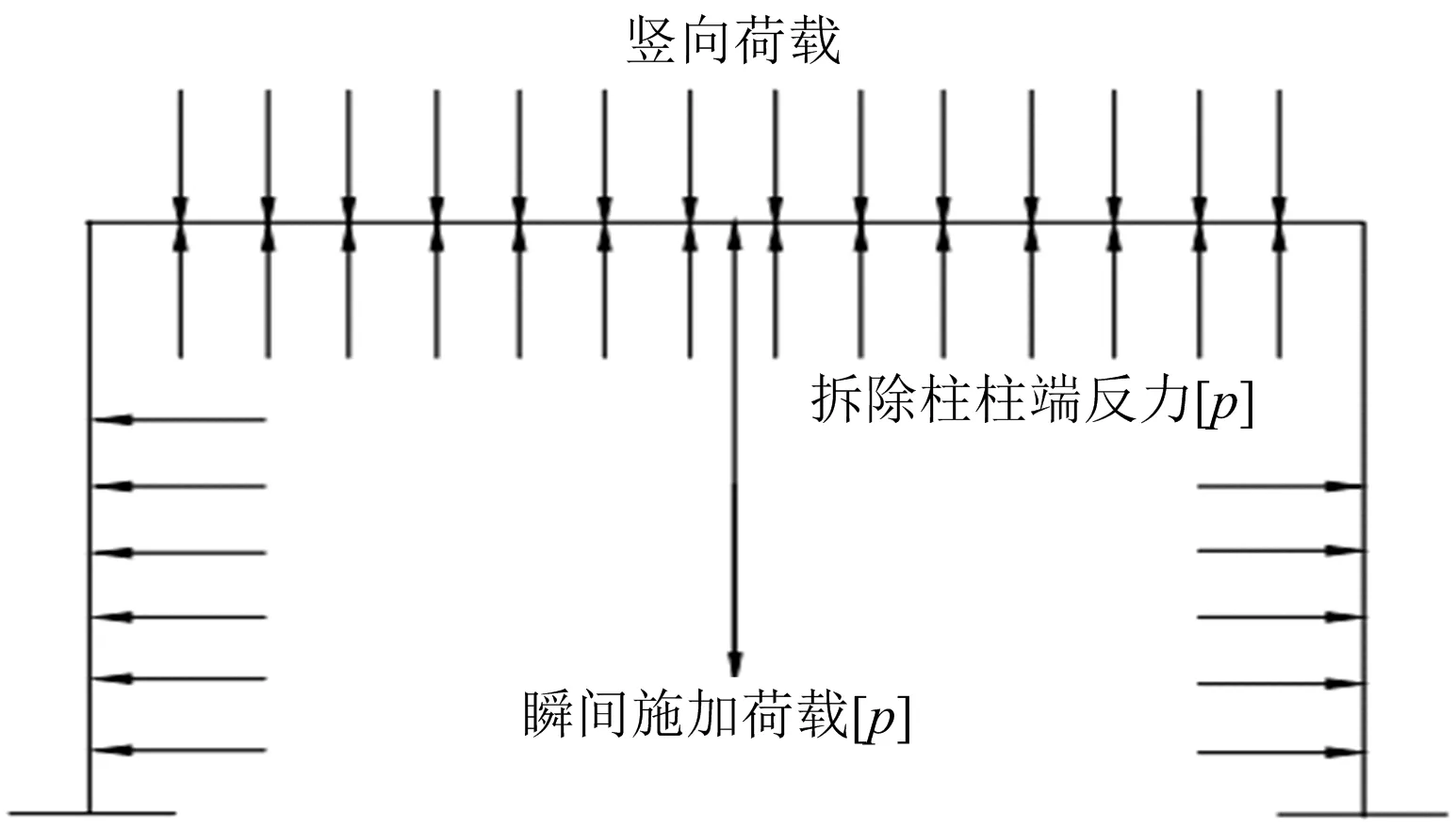
图6 拆除柱的动力荷载模拟Fig.6 Simulation of the dynamic load of the demolition column

4 数值模拟结果分析

1)时程位移分析。5 kg炸药当量和不考虑冲击波作用下各节点的位移时程如图7所示。

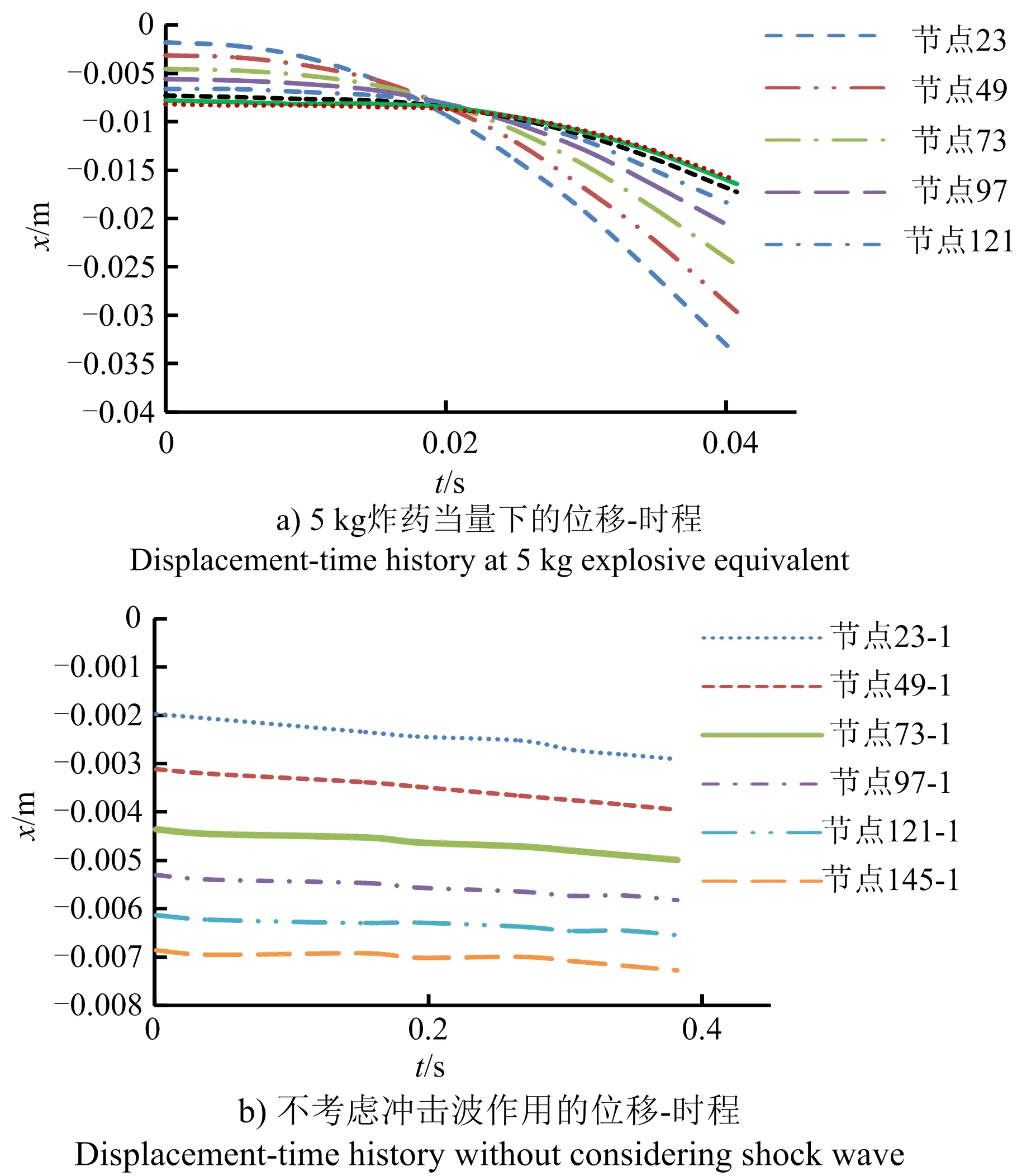
图7 梁柱节点位移-时程Fig.7 Beam-column node displacement-time history

在图7中，相比较图7b未考虑冲击波影响的位移时程，图7a各节点位移值均有所增大，其中23号节点(关键柱拆除点)用0.041 s的时间，位移值增长23.8%，并停止破坏，而图7b在不考虑冲击波作用的情况下，其破坏时间为0.26 s，破坏时间缩短了84.23%。

2)塑性铰分析。5 kg炸药和不考虑爆炸冲击荷载工况下的最后时刻塑性铰分布如图8所示。

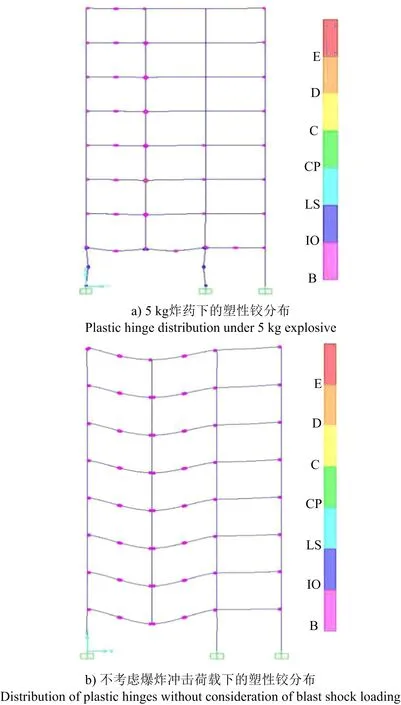
图8 2种工况下的最后时刻塑性铰分布Fig.8 The last moment of plastic hinge distribution under 2 kinds of working conditions

对比图8a、图8b，得出直接受爆炸冲击荷载的梁和柱均没有发生破坏，但5 kg炸药工况下的450柱和410柱出现塑性铰。由此可知，尽管炸药量很小，在分析受爆炸冲击荷载破坏的结构时，必须考虑冲击波的影响。

3)与利用ANSYS LS/DYNA等大型有限元软件进行显示动力分析相比，采用SAP2000进行建模更为简单、快捷，采用“构件失效+简化爆炸荷载直接作用”的方法避免了建立炸药、空气模型，不需考虑流固耦合作用以及负责边界问题，降低了“理论门槛”，提高了实用性，从一定程度上在精度和时效性、经济性之间进行了有效平衡，更适合广大设计人员使用和推广。