动车组铝板结构辐射效率与隔声量的关系研究

夏正志， 张 旗， 帅仁忠， 陈 彪

(1 中车青岛四方机车车辆股份有限公司， 山东青岛 266111；2 中国铁道科学研究院集团有限公司机车车辆研究所， 北京 100081)

1 辐射与响应的互易关系研究

铝板结构的声传播包含两个最基本的现象，一个是声波激励板振动，另一个是板的振动引起声辐射，因此需对板对激励的响应与板在激励下的辐射之间的相互关系进行研究，由于声波波长与实际物体尺寸接近时声波容易发生衍射，不利于降低噪声，而且实际中噪声的产生可能是多种声波共同作用的结果。主要考虑在局部的理性状态下，在声波波长远大于实际物体尺寸的情况下进行的研究计算。

辐射与响应的相互关系通过两个试验来获得，有一块曲板安装在一间混响室中，在试验1中用力F激励薄板，导致板的振动，进而产生声辐射。

图1 试验1的试验简图

理想状态下认为这个系统是线性传递的，此时房间中的辐射声功率将正比于板的均方振速，而均方平均振速又由激励力决定，因此有房间中的声功率表达式为：

W=α|F|2/2

(1)

式中α为辐射系数。

在混响室中，声功率表达式为：

(2)

此时将一块质量为m面积为S的圆盘放在混响室的另一侧墙上，并且它的尺寸远小于所讨论的频率对应的声波的波长，则圆盘受到力S|p|，产生的均方振速为：

(3)

综合以上3个表达式，得到圆盘的均方振速与板所受到的激励力平方的比值为：

(4)

再进行理想状态下试验2，模型与试验1相同，激励力的作用对象不同。

图2 试验2的试验简图

此时混响室中的圆盘受到激励力F′的激励，产生的均方振速为：

(5)

相应产生的体积速度的平方表达式为|q|2=S2|vs|2，因为上述假设圆盘的尺寸远小于声波的波长，因此可以知道此时圆盘受到激励力F′所产生的声辐射为：

(6)

由式(1)～式(2)可知此时混响室内的空间声压平方表达式为：

(7)

这时空间的声压又作用在混响室中的薄板上，同样假设系统为线性的，并假设响应系数为β，此时薄板的均方振速可表示为：

|v′|2=β|p′|

(8)

同样综合以上3个表达式，得到板的均方振速与圆盘所受的激励力平方的比值为：

(9)

结合上述试验1和试验2，由于试验中的激励与响应是互换的，又因为系统为线性系统，所以两个试验中响应与激励的比值应该相等，因此比较式(4)与式(9)得到辐射系数与响应系数的关系为：

(10)

等式右侧为常数表明，结构由声场激励而产生的振动速度响应由同样一块板在点激励力下产生的辐射声功率所决定，即结构的响应由它的辐射决定，结构产生的辐射由它受到激励力而产生的响应决定。

2 辐射效率与隔声量的关系

从隔声频率特性曲线上看，以临界频率为界分3个区域进行研究分析。

(1)次临界频率

在次临界频率区域中，有限大板的模态辐射效率受边界条件影响很大并且都远小于1，但是有限大板在模态下会发生共振，因此在模态频率下比较同样材料同样厚度的无限大板与有限大板时，会发现板的共振现象会严重影响板的声传递系数。

对各项同性，等厚度，等密度的板，无限大板的声传递效率与板共振时的声传递效率有以下关系式：

(11)

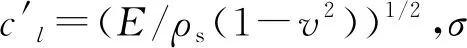
在次临界频率区域，简支矩形板的平均模态辐射效率有以下表达式：

σ≈(Pλc/π2A)(f/fc)1/2

(12)

式中P为板的周长，A为板的面积，fc为板在临界频率下的波长，将此式代入式(11)得：

τ∞/τr≈200(A/Pλc)2ηtot

(13)

从式(13)看出，除非对小阻尼，轻质，大刚度的板外，式(13)是远大于1的，由于有限大板的共振现象，要获得有限元大板的隔声量表达式比较困难，但是如果不考虑板的模态频率下的共振时，Sewell在1970年推导得出面积为A的板，不考虑共振时，在次临界频率区域，它的隔声量表达式为：

TLnr≈TL(0)-10log10[ln(kA1/2)]+

20log10[1-(ω/ωc)2]

(14)

式中的下标nr表示non-resonant。

(2)临界频率之上

从式(8)可知，板在受声波激励的激励参数为β，考虑到混响室中均方声压|p|2在面积S上产生声功率Wi=|p|2S/8(ρ0c0)，然而以均方振速|v|2振动的板在另一侧产生的声辐射为Wt=|v|2ρ0c0Sσ/2，此时声传递系数可表示为：

(15)

由于辐射效率σ随频率变化差异很大，并且对于不同的激励，板的辐射效率也会不同，当频率高于临界频率时，板相应的结构辐射效率趋于1[1-4]，因此此时声传递系数的表达式变为：

(16)

式(16)说明一块各项同性的板的声传递系数可以直接由它的辐射系数所决定。现假设一块板受到点激励力，考虑板的损耗因子η时，板的均方振速为：

(17)

由式(1)可知此时薄板产生的辐射声功率为：

W=α|F|2/2=ρ0c0S|v|2/2

(18)

通过式(18)求出辐射参数α，代入式(16)得到板在受到点激励时的声传递系数为：

(19)

(20)

式(20)就是频率高于临界频率时，板的隔声量。

从式(20)中可以看出，①隔声量随着板的质量变大一倍而增加6 dB，这说明有限大板在频率高于临界频率之后，它的隔声量曲线与质量定律平行；②此时的隔声量与临界频率及板的混响时间也有着很大的关系，由于损耗因子不仅与材料的属性有关，还和板的边界条件有关，对不同的边界条件，隔声量的变化在6 dB上下。

(3)临界频率附近

当感兴趣的频率位于临界频率附近的区域时，此时有声压引起的板面振动速度为：

(21)

式(21)并不能直接得到声传递系数，但可以看出式(21)右侧括号中的前一项表示被激励的振动的波长与声波入射波长一致的情况，第二项代表板被声波激励起的其他弯曲波。当板被激励起来的振动的波长与声波入射波长一致时辐射效率σE≥1，而板被激励起来的其他弯曲波的辐射效率σF<1。

将式(21)代入式(15)得临界频率区域板的声辐射系数表达式为：

(22)

由式(22)同样可以看出，阻尼是影响临界频率区域的声辐射系数主要因素。

为得到辐射效率与隔声量随着频率的变化趋势，并从定性的角度上观察两者之间的关系，现将隔声量与辐射效率归一到一张图中，结果如图3所示，图中红色曲线为板的辐射效率，蓝色曲线为板的隔声量随频率比变化的趋势线。

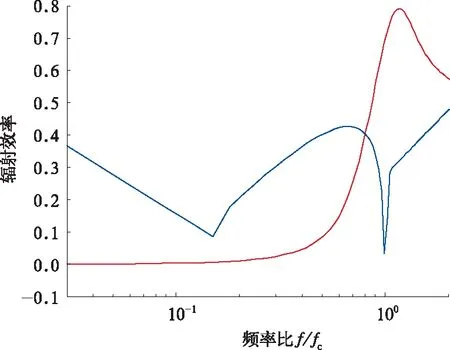
图3 隔声量与辐射效率的比较

从图3中可以看出辐射效率有一个峰值，而隔声量有两个低谷。辐射效率的峰值表示当频率比1时，板发生吻合效应，辐射效率增大。隔声量曲线的第一个低谷代表板在固有频率下产生共振导致隔声量下降，而第二个低谷表示频率比为1时，吻合效应使板剧烈振动，导致隔声量下降。这说明板的共振对辐射效率并无影响，但会导致隔声量下降；而板的吻合效应同时影响着辐射效率与隔声量两个因素。

以上以临界频率为界分别讨论了板的辐射效率与声传递系数的理论关系，进一步给出了相应情况下板的隔声量表达式，并从定性的角度指出辐射效率与隔声量的关系。

3 铝板的隔声量与辐射效率试验

前面从理论上进行了板块辐射效率的研究，本节通过对板的试验来验证上述关系，分别进行铝板的辐射效率试验，试验对象铝板的尺寸为a×b×h=1.5×1.2×0.003(m)，材料属性有弹性模量E=7.0×1010Pa，密度ρ=2 700 kg/m3，泊松比μ=0.3，损耗因子η=0.01。两个试验都在隔声室中进行，隔声室由发射室与接受室组成。

3.1 隔声量试验

试验简图如4所示。

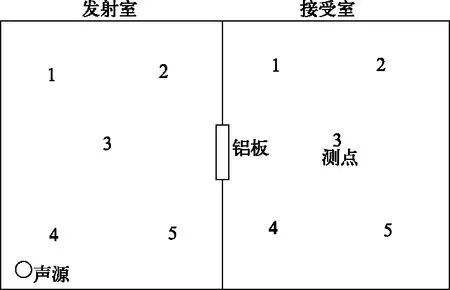
图4 隔声量试验简图

在发射室进行白噪声声源激励，分别在发射室与接受室测量5个点的声压值，得到它们的室内平均声压级：

(23)

测得发射室内的平均声压级为L1，接受室内的平均声压级为L2。

(24)

为避免人为试验误差，进行了3次隔声量测试试验，运用式(24)得到3次试验的铝板隔声量如图5所示。

从图5看出，3次试验除在低频处有些许的差别外，其他频率下基本相同，因此本试验的数据有效，3次试验的计权隔声量分别为29.45 dB、29.47 dB、29.10 dB。

图5 3次试验的铝板隔声量

图6 试验隔声量与理论隔声量对比图

图6中红色实线为测量值，蓝色虚线为质量定律，蓝色竖线对应吻合频率，从图6中可以看出试验数据与质量定律吻合的非常好，并且吻合频率结果也比较一致。

3.2 辐射效率试验

通过前面的理论分析，了解到要得到一块板的辐射效率的最简单的方法是知道板的平均振动速度及板产生的辐射声功率。本试验在隔声室中进行，通过在发射室进行白噪声激励，测量接受室内的平均声压作为板的辐射声功率；在同样的激励条件下测量板面上的48个点的加速度响应，作为板的平均振动速度，板的测点示意图如图7所示。

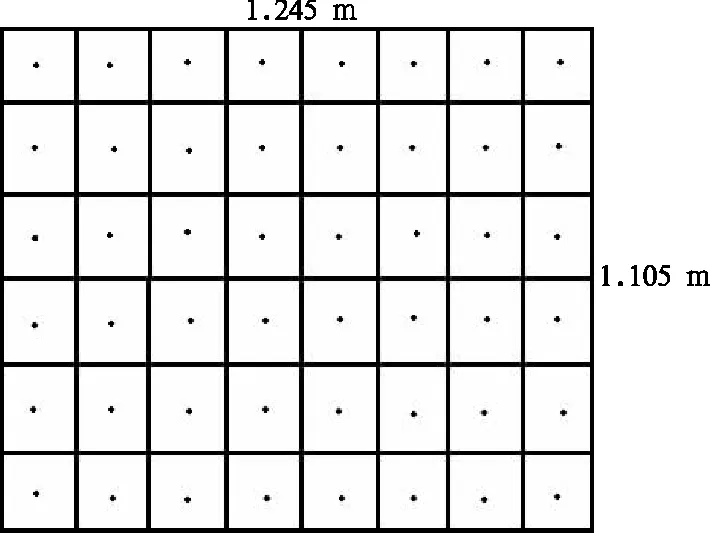
图7 板的测点示意图

将试验中测得的接受室内5个测量点15个试验数据导出，计算得到对应的声功率，进而求出15个试验数据的平均值，结果如图8所示。

图8 接受室的总数据与平均值：红色为平均值，蓝色为15个试验值

从图中看到，红色的平均值曲线基本上可以代表15次测量数据计算得到的声功率。

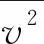
(25)

由于均方振速的数量级较小，为便于观察取均方振速级：

(26)

本试验48个点的均方振速级如图9所示。

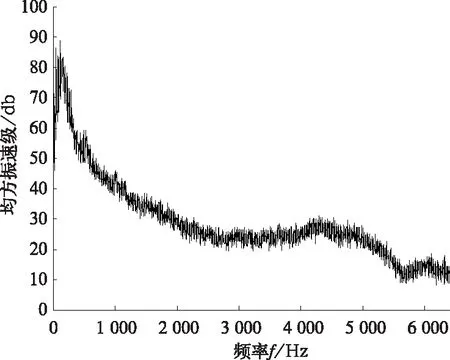
图9 48个测点的均方振速级

由式(2)与式(3)，可知本试验的薄铝板在接收室产生的声辐射表达式为：

(27)

下面将试验测的声辐射与上式理论计算的声辐射进行对比，对比结果如10所示。

图10 试验声辐射与计算声辐射对比图

图10中红线为试验结果，黑线为计算结果。从图10中可以看出，试验测得的声辐射与理论计算的声辐射值有着同样的趋势，验证了上述的理论推导的正确性，图中低频区试验值大于理论计算值，这是因为低频声波的波长很大，而试验中板的边界难免会存在着小孔，因此这一现象是由与低频声波通过孔衍射而产生的。

4 结 论

通过对铝板的辐射效率与隔声量进行研究分析，得到了铝板的模态辐射效率计算公式，给出了板在给定振动分布下产生的声辐射理论表达式以及临界频率附近声辐射效率与隔声量的变化情况。同时通过试验，对上述的理论推导进行了验证，试验结果表明隔声量与质量定律相吻合。主要针对局部简易板结构从定性的角度指出辐射效率与隔声量的关系，为板的声振特性分析提供一定的理论基础。适用范围同时具有一定的局限性，适用于局部单一板结构的分析。对于复杂的多结构还有待后续继续研究。