基于改进MSCKF 算法的室内机器人定位方法①

孙 弋, 张雪丽

(西安科技大学 通信与信息工程学院, 西安 710054)

引言

机器人实现应用的关键可概括为3 个核心问题:我在哪、我要去哪和如何去[1]的问题, 其中“我在哪”的定位问题是首要问题[2], 而且随着机器人在矿井[3]、医疗[4]、服务[5]等领域的应用, 定位精准性的需求逐渐成为人们研究和关注的重点[6,7].由于单一传感器的定位精度和可适用性有限, 目前, 机器人定位普遍采用将多种传感器数据进行融合的方式实现[8-11], 其中惯性测量单元(IMU)和相机(camera)存在互补性[12], 因此IMU和Camera 传感器的数据融合方式受到了更多青睐.

IMU 和Camera 数据融合问题又称为VIO (Visual-Inertial Odometry)问题.目前, 基于滤波的主流VIO 算法有: Multi-Sensor Fusion (MSF)、Multi-State Constraint Kalman Filter (MSCKF)、Robust Visual Inertial Odometry (ROVIO)等.其中MSCKF[13]是2007 年由Mourikis 等提出的算法, 该算法采用扩展卡尔曼(EKF)[14]将IMU 和单目Camera 传感器数据进行EKF 融合, 融合方法是用IMU 运动模型构建EKF 状态方程, 用单目Camera 的重投影误差建立EKF 量测模型.

近年来, 随着机器人行业的迅速发展, 关于MSCKF算法的研究有许多进展.文献[15]从计算代价角度, 集成了EKF-SLAM 和MSCKF 两种算法.首先预测每个特征分配策略的计算成本, 然后制定目标函数, 最后用目标函数的最小化决定定位系统所使用的融合策略.该算法对状态向量也进行了增广, 使得当系统进行更新时, 长时间跟踪的特征点能及时得到利用.文献[16]是将原来的单目Camera 改为立体Camera, 提高定位的稳健性, 并且边缘化采用Two-way Marginalization策略, 考虑了无人机应用中悬停等特性.文献[17]利用了全方位摄像机获得球形图像, 从更宽的视眼内获得更多的视觉特征与IMU 测量相结合, 避免因环境纹理不足造成定位效果不佳的问题.文献[18]在初始化阶段应用sigma 点滤波器, 使得当机器人初始化阶段遭受冲击时定位与导航性能仍然可靠.

本文针对传统MSCKF 算法使用的IMU 中加速度计传感器的自身缺点: 测量信息中包含重力信息, 且算法在执行时无法很好的将重力加速度有效去除[19];速度和位置状态方程经积分解算得到, 存在偏置漂移累计和距离测量精度随时间恶化[20]等问题, 提出了改进MSCKF 算法.改进的MSCKF 算法用轮式里程计(Wheeled Odometer, 后续使用W-Odom 表示)取代加速度计传感器, 利用W-Odom 对机器人运动的平移数据测量较为稳定和准确的优点[19], 改进传统MSCKF算法的EKF 状态方程.改进的EKF 状态方程使用陀螺仪构建姿态方程, 使用轮式里程计构建速度和位置方程, 避免状态方程受重力干扰和由于积分产生累计误差的问题, 使预测更有效, 从而提升定位精度.

1 MSCKF 算法

MSCKF 是基于EKF 滤波的IMU 和Camera 的数据融合算法.在介绍MSCKF 算法之前, 首先需要对相关的坐标系进行定义和约定.在本文中, I 表示IMU 坐标系, 又称为载体坐标系, 与载体固连, 随载体运动而变化; C 表示相机坐标系; G 表示全局坐标系, 是固定不变的坐标系, 本文定义G 系在算法的初始位置, 即是以机器人中心点位置为原点, z 轴为垂直载体向上,x 轴指向载体的前部, y 轴指向载体的左侧.上述坐标系均满足右手定则.

MSCKF 算法的系统状态向量X 定义为:

MSCKF 算法的EKF 状态方程使用IMU 数据对系统状态向量进行预测.IMU 测量输出的数据是角速度 ω和线加速度 f , 将其经坐标转换可得到角速度和线加速度在IMU 坐标系下的表示, 这其中包含了陀螺仪和加速度计的零偏 bω、 bf以及噪声 wω、 wf, 因此真实的角速度和加速度定义为:

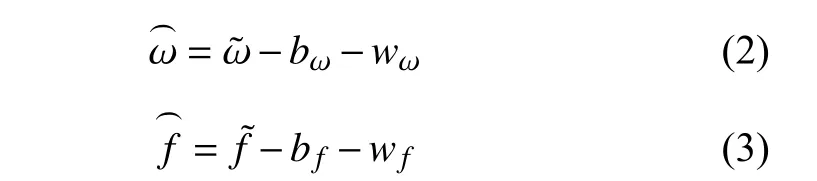
MSCKF 算法的状态方程推导较为复杂, 本文直接给出连续状态方程, 具体推导过程见文献[21]:

式(4)为姿态状态方程, 式(6)为速度状态方程,式(8)为位置状态方程.通过对上述方程采用积分方法即可实现对系统状态向量的预测.

2 MSCKF 算法的改进与实现

2.1 改进MSCKF 算法

由传统MSCKF 算法的EKF 状态方程可以看出,速度方程受重力影响, 且是对加速度计测量的线加速度数据和重力加速度进行积分得到, 位置状态方程是对速度再次积分, 即对线加速度数据进行两次积分得到, 这使得速度和位置方程受重力干扰, 且位置漂移随时间二次增长.针对此问题, 本文利用W-Odom 传感器以及IMU 中陀螺仪的互补性: 陀螺仪测量的角速度短时间内精度较高, W-Odom 对平移测量较为准确, 以及室内环境特点: 机器人在二维平面内运动, 替换EKF状态方程中的式(6)和式(8), 改进MSCKF 算法.

首先分析W-Odom.已知本文实验使用的Turtlebot2机器人采用两轮差速底盘控制, 轮子半径为r, 左右轮之间距离为 L, 轮子行走一圈编码器的总脉冲数为sum,设 Δt 时间内左右编码器输出的脉冲数为 NL、 NR, 左右轮的线速度为 VL、 VR, 机器人的速度v 与角速度 ω0, 由式(11)-式(17)可计算出机器人的速度 v 以及位置x、y.其中式(13)为速度方程, 式(16)和式(17)是WOdom 位置方程.

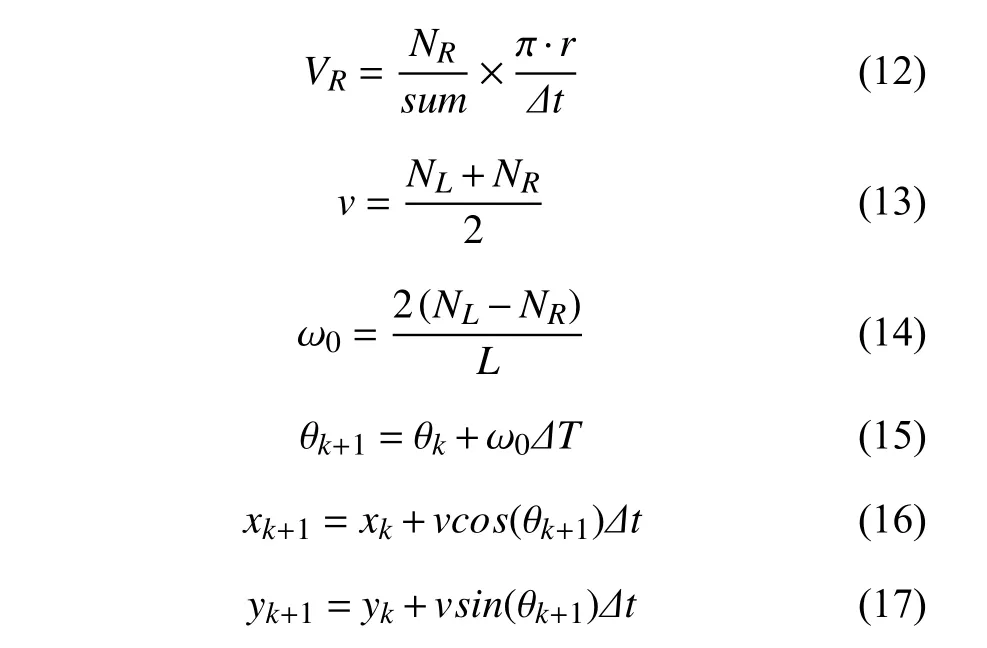
改进MSCKF 算法首先用W-Odom 的速度方程式(13)替换EKF 速度状态方程式(6); 其次用EKF 姿态状态方程式(4)求得姿态角中的航向角, 并用代替W-Odom 的位置方程式(16)和式(17)中的θ, 改进位置方程, 最后用改进后的位置方程替换EKF 位置状态方程式(8), 即得到改进的MSCKF 算法.改进MSCKF 算法舍弃IMU 中加速度计的使用, 综合利用IMU 中陀螺仪和W-Odom 的各自特点, 将两种传感器数据进行融合, 改进传统MSCKF 算法的EKF 状态方程, 适用于机器人在室内的运动.

2.2 MSCKF 与改进MSCKF 算法的实现

2.2.1 MSCKF 与改进MSCKF 算法的实现流程

MSCKF 算法通过IMU 数据预测状态向量, 通过单目Camera 对环境进行观测, 提取自然路标, 并运用路标信息的重投影误差约束对预测的状态信息进行修正更新.如图1 是传统MSCKF 算法的流程图, 图中的英文对应的是程序里不同的函数.

判断10 s 内是否有新一帧图像.若在10 s 内无图像帧到来, 则MSCKF 算法停止状态量更新, 结束; 若有新一帧图像到来, 则进行下一步.

(1) 判断是否初始化.若没有完成初始化, 则进行初始化, 并构造MSCKF 状态向量, 进行下一步; 若已经完成初始化, 则直接进行下一步.

(2) EKF 预测.传统MSCKF 算法输入为IMU 数据, 调用根据第1 节EKF 状态方程编写的函数, 输出系统状态向量的预测值和对应的协方差矩阵.

(3) 对新图像进行光流跟踪、匹配, 并提取新的特征点.

(4) 将新一帧图像的位姿pose 加入到状态向量和协方差中(增广).

(5) 特征点处理.

① 若之前视图中的特征点在当前帧中观测不到(看不见的特征点), 则将该特征的跟踪列表加入到measurementUpdate 中, 用于更新MSCKF 状态向量.

② 若当前帧观测到的特征是之前在视图中已经观测到的特征点(成熟特征点), 则将该特征点加入到跟踪列表.

③ 对新提取的特征点分配新的featureID, 加入到跟踪列表.

(6) 循环遍历所有加入到measurementUpdate 中的特征点, 进行EKF 更新, 得到MSCKF 系统状态向量的最优解.

① 对特征点进行三角化, 精确得到当前路标点在全局坐标系的位置.

② 特征点的边缘化: 将重投影误差中的关于特征点误差的约束进行边缘化(左零空间投影), 将特征点误差约束转化为系统状态向量的约束(待优化变量).

③ 利用重投影误差, 采用视觉更新, 进行一次线性化, 求解当前帧时刻系统状态向量的最优解.

(7) 将滑动窗口滑图像帧进行边缘化, 使其维持在固定的长度.

图1 传统MSCKF 算法流程图

以上是MSCKF 算法的流程图.改进MSCKF 算法是在原算法基础上, 对第二步EKF 预测部分的状态方程进行改进.改进算法的输入为W-Odom 数据和IMU 中陀螺仪的数据, 且执行的函数(方程)不同, 执行的函数为im_propagate.

由此, 可以完成一次对当前时刻机器人位置的估计, 当新一帧图像到来之后, 循环执行此步骤, 即实现MSCKF 算法及其改进算法.

2.2.2 MSCKF 与改进MSCKF 算法的实现

本文使用Turtlebot2 机器人, 在装有Ubuntu 16.04机器人操作系统(ROS)的Lenovo G50 笔记本电脑上进行实验测试.如图2 所示, 是带有kokuki 底盘的Turtlebot2 机器人, 内置了IMU 和轮式里程计传感器,在此基础上外加单目相机和核心处理器Intel i5, 就组成了实验硬件.ROS 是实现机器人定位的软件部分.ROS 可提供用户、计算机操作系统以及外部设备间的通信功能, 并集成了一系列定位、导航等行为的工具和库, 能够在不同的机器人平台(如Turtlebot)上辅助研究人员进行机器人系统相关的研究和开发, 创建定位、导航等复杂的机器人行为.

图2 Turtlebot2 机器人

本文使用的MSCKF 及其改进算法以msckf 和im_msckf 包封装在ROS 内.MSCKF 及其改进算法首先订阅陀螺仪、轮式里程计、单目Camera 发布的话题, 然后执行根据2.1.1 节编写的算法处理数据, 并以msg 格式发布msckf 和im_msckf 话题.最后在Ubuntu 16.04 系统上编写msckf.py, 该文件订阅MSCKF 及其改进算法发布的话题, 并以txt 形式输出MSCKF 及其改进算法计算的机器人位置坐标.

MSCKF 及改进算法有两个比较重要的文件:src/ros_interface.cpp 和src/cornet_detector.cpp.其中src/ros_interface.cpp 是算法主体, 包括状态预测、状态增广和测量更新等步骤.src/cornet_detector.cpp 是视觉前端处理部分, 主要进行光流跟踪及特征点处理等操作.

3 实验结果分析

本文采用两种策略验证改进MSCKF 算法的有效性: 一种是使机器人做规定轨迹运动, 用Matlab 读取TXT 数据, 绘制运动轨迹图, 对比真实轨迹与算法轨迹, 直观的观察机器人运动过程中的定位精度; 第二种策略不关注机器人的真实运动轨迹, 关注机器人运动时间长短与闭环定位精度的关系, 因此使机器人做闭环轨迹运动, 并将(0.00, 0.00)与算法计算的终点位置的距离作为衡量定位准确度的指标(闭环误差), 绘制闭环误差表, 统计平均闭环误差.其中机器人运动的实验环境为实验室和走廊两种环境, 如图3 所示.

图3 实验环境

3.1 规定轨迹运动

遥控使机器人做封闭规定轨迹运动, 实验运动环境为图3(a).实验前预先在路径上设置4 个坐标点(0.00,0.00)、(3.80, 0.00)、(3.80, 2.70)、(2.70, 0.00), 规定机器人路线为矩形, 运动距离为13 m, 且各坐标点之间的运动为直线, 运动一圈后回到起点位置(0.00, 0.00).

图4 为一次实验Matlab 绘制的运动轨迹图.图中五角星为机器人起点及终点位置, 直线轨迹为规定的机器人运动轨迹, ×号轨迹为使用传统MSCKF 算法的IMU/Camera 运动轨迹, 圆圈轨迹为改进MSCKF 算法的IMU/W-Odom/Camera 运动轨迹.图中可直观的看出, 改进MSCKF 算法的整体运动轨迹更接近真实轨迹, 计算的终点位置也更接近起点(0.00, 0.00).

3.2 封闭轨迹运动

遥控使机器人在走廊内从起点(0.00, 0.00)开始运动, 最后回到起点(0.00, 0.00), 即做闭环轨迹运动, 且实验中机器人的运动为直线和转弯的结合.为更好的分析闭环定位误差, 减小由于运动时间、环境、操作误差和偶然性对实验结果的干扰, 本文在两种环境下进行了运动时间不同的5 次实验, 其中, 实验2 和实验4 实验环境为图3(a), 其余实验环境为图3(b), 统计的运动闭环误差如表1.表中x、y 表示算法计算得到的终点坐标, 闭环误差是该终点坐标与起点(0.00, 0.00)的距离.

图4 规定路线运动轨迹

表1 闭环误差

对比实验1-实验4 的结果可以看出, 实验2 和实验4 的运动时间较长, 但其定位精度优于实验1 和实验3, 说明在特征纹理丰富环境, 单目Camera 在更新时可选取的有效特征点较多, 使得MSCKF 算法定位效果优于特征贫乏环境.由表1 中可以看出, 改进MSCKF 算法定位精度优于传统MSCKF 算法, 平均闭环误差提升了0.081 m, 定位精度提升, 说明改进MSCKF算法使用轮式里程计对平移运动的约束比加速度计好,改进MSCKF 算法的定位结果更优.

4 结束语

针对传统MSCKF 算法实现机器人室内定位时加速度计传感器的固有缺点: 受重力干扰和需积分解算得到速度和位置方程的问题, 本文提出了改进MSCKF算法.改进算法使用轮式里程计取代IMU 中加速度计传感器, 替换传统MSCKF 算法中EKF 速度和位置状态方程, 使EKF 预测更加准确.同时将MSCKF 及其改进算法封装在ROS 内, 结合Turtlebot2 机器人实现算法并进行实验验证.通过对实验结果分析得到, MSCKF算法及改进MSCKF 算法在特征纹理丰富环境中的定位效果要优于特征贫乏环境, 且改进MSCKF 算法的整体运动轨迹更接近真实轨迹, 闭环误差也优于传统的MSCKF 算法, 这为后续室内机器人进行自主导航和路径规划提供了更好的前提.