基于改进回声状态神经网络的个股股价预测①

李 莉, 程 露

(江苏大学 计算机科学与通信工程学院, 镇江 212013)

1 引言

股市发展趋势的变化在一定程度上反应了国民经济的强弱, 因此, 几十年来, 对股市预测的研究是人们关注的重点之一.20 世纪, 国外的学者提出了ARMA系列模型, 该模型能较好地处理线性稳定性问题, 在很长一段时间里, 成为了预测研究的热点, 但是股市中遇到的大多是非平稳和非线性的, ARMA 系列模型不能很好地处理这些问题.20 世纪后期, 一些学者提出ARIMA 模型, 在ARIMA 模型的基础上对该模型进行了改进.以提高模型预测的精确度.

近些年来, 随着预测技术的逐步发展, 神经网络模型开始被人们应用到股价的预测研究中.神经网络具有良好的自适应能力和较强的非线性逼近能力, 能够较好地解决股市中存在的非线性和非平稳的特点.Göçken M 等[1]运用混合人工神经网络模型研究了股市指标与股市之间的关系.Adebiyi AA 等[2]对ARIMA模型和人工神经网络模型进行了对比研究, 利用股票数据进行了实验, 对比了两者的预测性能.卢辉斌等为了提高预测的准确性, 运用改进的PSO 对BP 神经网络进行优化[3].由于经典的神经网络预测模型(如BP神经网络), 使用梯度下降算法完成对权值和阈值的训练, 但是, 如果没有选择正确的初始位置, 该算法将陷入局部最小值, 无法获得全局最优解.2004 年Jaeger 等[4]使用回声状态神经网络对时间序列进行了预测, 同比于之前的实验, 效果得到了显著的提高.

回声状态神经网络(ESN)是递归神经网络的一种,递归神经网络拥有较好的非线性学习能力, 当前已成为时间序列预测的主流工具, 并且得到了学者们的认可, 但经典的ESN 学习能力有限, 当用于实际问题下进行预测时, 其泛化能力有待提高.

针对以上缺点, 本文提出一种基于改进的回声状态神经网络(ESNGTP)的个股股价预测模型, 使用改进的粒子群算法(GTPSO)对ESN 的输出连接权进行搜索, 获得较优输出连接权, 进而提高算法的学习能力.

GTPSO 算法是在经典的PSO 算法搜索的过程中,引入了禁忌搜索算法(TS)中禁忌的思想和遗传算法(GA)中变异的思想, 降低PSO 陷入局部最小值的状况, 同时提高PSO 搜寻全局的能力.

2 回声状态神经网络(ESN)

ESN 是递归神经网络的一种, 如图1 所示.

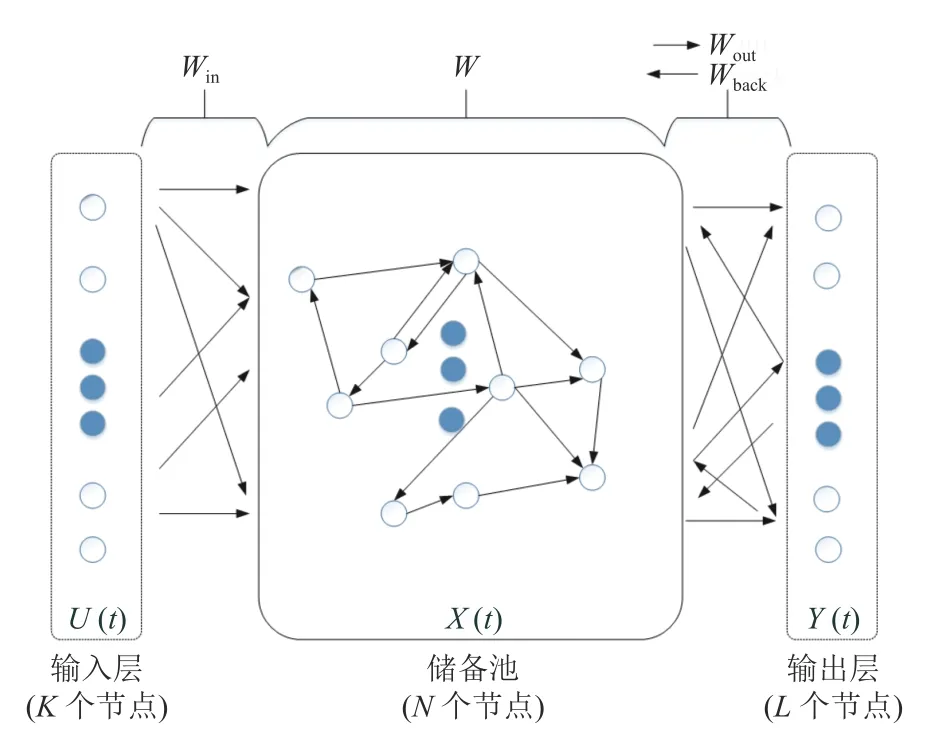
图1 ESN 结构图

ESN 有3 层: 输入层、储备池和输出层, 其中ESN 的储备池, 在训练过程中, 它类似于传统神经网络的隐层.拥有 N 个节点, N的数值较大.因此, 它拥有一定的短期记忆能力.ESN 的输入和输出则分别有K 和L 个节点.图1 中输入层与储备池之间的反馈用 Win表示, 储备池内部反馈矩阵用 W表示, 储备池到输出层的反馈以及输出层到储备池之间的反馈则分别用 Wout和Wback表示.当t 时刻时, 输入层的输入为u(t)=[u1(t),u2(t),···uK(t)]T, 储备池内部状态为x(t)=[x1(t),x2(t),···xN(t)]T, 输 出 层 的 输 出 为 y(t )=[y1(t),y2(t),···yL(t)]T,xt和 yt的计算方式如式(1)和式(2)所示, 其中 f和F(·)为对应的激活函数.

ESN 在训练的过程中, Win, Wback和 W是随机初始化生成, 确定后将不再改变, 然而 Wout是通过训练生成的, 所以, ESN 的学习过程能够看作是 Wout的确定过程.

ESN 的核心是用大规模的递归神经网络代替传统神经网络的隐层.某种意义上, 降低了算法因递归下降而陷入局部最小值的状况, 同时减少了训练过程中的计算量.但是在ESN 的学习过程中, 如果数据集略有偏差, 最终结果变化会较大, 存在过拟合和泛化能力降低等问题.

3 粒子群优化算法(PSO)

粒子群优化算法(PSO)首先是由Kennedy 等[5]在1995 年提出, 该算法将搜索最优解的过程看成是鸟类觅食活动.一群鸟在一个地区寻找食物, 假设该地区只有一个食物.这些鸟之间相互分享信息, 并且它们知道自身的位置以及自身距离食物的位置, 但是它们不清楚食物的位置.PSO 从这一活动中受到了启发, 将每只鸟看成是一个拥有速度与位置的粒子, 食物是最优位置, 寻优的问题则看成是所有粒子在多维空间中搜索的过程.

假定PSO 在 n 维空间中进行搜索, 将食物视为最优解, 所有的粒子都清楚它们自身的位置.同时, 能够依据适应度的值( fit nessi)判断位置的优劣.粒子根据它们自身的经验和群体的经验更新粒子的速度和方向.直到能够达到停止条件为止.PSO 在搜索的过程中, 速度快, 结构简单, 在网络优化和函数训练中, 应用广泛.首先对i 个粒子进行初始化, 粒子i的位置矢量和速度矢量分别记做 Xi=(xi1,xi2,xi3···,xin) 和Vi=(vi1,vi2,vi3···,vin) , 粒 子i 的 自身 最优 解 为 Pbest, 记为Pi=(pi1,pi2,pi3···,pin), 群体最优解为Gbest, 记为Gi=(gi1,gi2,gi3···,gin) , 在迭代迭代期间, 粒子依据以下公式更新 Xi和 Vi.

其中, k 代表迭代期间的步骤, c1和 c2为学习因子.文献[6]中总述了粒子群(PSO)在1995～2017 年的研究进展、改进、修改和应用, 这里不再一一复述.

在PSO 的搜索过程中, 粒子之间会互相分享信息.这样的分享方式可以让粒子在刚开始的时候拥有较快的收敛速度.但是在迭代的后期, 粒子的更新受到限制,速度变慢, 陷入局部最优的状况增大.

4 禁忌搜索算法

禁忌搜索算法(TS)[7]首先是由Glover F 等1986年提出, Glover 在文献[8,9]中提出了大部分禁忌搜索使用的原则.禁忌搜索算法如今被广泛使用于解决路径规划和排序等问题, 例如Zhang 等利用改进后的禁忌搜索算法[10]解决了汽车排序问题.

TS 模拟人的记忆思维模式, 本质上, 它是一种全局逐步最优搜索算法.在搜索的过程中将过去搜索的方案存储在禁忌表中, 为了避免重复, 使用禁忌即禁止的方法, 这减少了搜索陷入局部最优的状况.同时在邻域的方案中选择最优的方案, 并且引入特赦的原则, 释放符合原则的禁忌对象, 可以在一定程度上避免搜索过程中因为早熟而达到局部优化.

禁忌搜索的核心是禁止重复之前的操作, 降低陷入局部最优的概率, 但是TS 容易过分依赖初始解, 同时, 还需要提高全局搜索的能力.

5 GTPSO 算法思想

传统的PSO 在搜索的过程中容易发生群体粒子集体向当前最优解飞行的现象, 进而出现粒子过早收敛的情况, 提高了算法陷入局部最小值的状况.为此,提出改进的PSO 算法—GTPSO 算法.通过引入TS 中禁忌的思想, 使粒子逃离局部最优的束缚, 同时为了增强PSO 对全局的搜寻能力, 引入GA 中变异的思想, 并且根据repeatStep 的变化状态来判断是否变异, 变异率ρ可以取0.01 到0.1 之间的数, ρ的增加在扩大搜索的范围的同时也会加长搜索的时间, 经过实验证明, ρ取0.04 可以得到较好的结果.传统使用GA 算法对PSO 算法进行优化时, 是在每次迭代的过程中均发生变异, 这样容易破坏粒子的结构, 并且减低了搜索的速度.基于此, 本文采用repeatStep 来判断是否发生变异,只有当粒子群聚集严重时才会发生变异, 扩大了粒子搜索的范围, 同时搜索速度相比于传统的GA 算法对PSO 算法的优化有所提升.

GTPSO 算法思想如下:

Step 1.初始化 Xi, Vi, 迭代次数 Iter, 连续不发生改变次数的阈值 M axstep[11](经过多次实验可知 Ma xstep=10 可以取得较好的结果), 粒子群规模( m =20), m数量的多少影响着搜索的范围和计算量, 取值范围一般在20 到40 之间, 经过实验可知, m取20 可以得到较好的结果.设置粒子群维度n, ρ=0.04, 学习因子c 1=c 2=2, 设置禁忌列表( TL), T L长度设置为100.

Step 2.计算PSO 中每个粒子的 fit nessi, 同时寻找PSO 最优适应度值( fit nessbest ), Gbest和 Pbest, 记录粒子群上一次最优适应度值( fit nessbestbe fore).

Step 3.判断 fit nessbest连续不变的次数是否超过Maxstep , 如果是, 则按照变异率 ρ对粒子群中每个粒子的 Xi和Vi重新初始化, 同时更新 fit nessi, fitnessbest,Gbest, Pbest, r epeatS tep, 否则转Step 4.

Step 4.判断当前 fit nessbest的值是不是小于fitnessbestbe fore 的值, 如果不是, Gbest不发生改变, 更新 Vi, Xi, fitnessi, fitnessbest , Gbest, Pbest, Vi, Xi,repeatS tep, 如果是转Step 5.

Step 5.判断当前 fit nessbest 的 值是不是在 TL 中,如果不是将当前 fit nessbest 的值加入 TL中, 同时更新TL, 否则转Step 6.

Step 6.用该次迭代的次优解取代Gbest, 同时判断该次迭代次数是否超过最大迭代次数, 如果是输出最优的Gbest, 如果不是转Step 2.

GTPSO 算法思想如图2 所示.

图2 GTPSO 混合算法流程图

GTPSO 伪代码如下:

输入: Iter, m, n, TL , Maxstep, c1, c2,ρ输出:Gbest初始化:Randomly initialize Vi andXi Initialize TL for Iter from 1 to Iter do ifIter==1 update fitnessi , fitnessbest, G best ,Pbest

end if if r epeatS tep＞ =Maxstep repeatStep=0 for it from 1 to n for it from 1 to m按照ρ 对 Vi 和 Xi 重新初始化u p d a t e fitnessi , fitnessbest , fitnessbestbe fore , Gbest , P best,repeatS tep(连续不变化的次数)end for end for end if if fitnessbest ＜fitnessbestbe fore if fitnessbest 在TL 中用次优解取代Gbest else 将 fit nessbest加入TL update TL end if else G best不发生改变for it from 1 to n for it from 1 to m update Vi ,Xi update fitnessi , fitnessbest , fitnessbestbe fore , Gbest , P best,repeatS tep(连续不变化的次数)end for end for end if end for

6 改进的回声状态神经网络

针对ESN 的泛化能力有待提升的特点, 本文提出一种改进的回声状态神经网络算法—ESNGTP 算法.Dutoit 等[12]把对ESN 的 Wout的优化看做是特征子集选取过程, 本文中使用GTPSO 算法完成对ESN 的Wout的选择, 增强了ESN 的泛化能力.

首先把ESN 储备池和输入神经元的数量之和作为PSO 的维数.接着把ESN 的误差函数作为PSO 的适应度函数, 然后将最优值作为ESN 的 Wout.

ESNGTP 算法思想如下.

Step 1.初始化ESN 的参数以及、 Win和W , 其中Win和W 是随机生成的, 一旦确定, 不再改变.同时初始状态 x(0)设置为0, 加载样本数据到输入与输出, 更新x(t) , 确定优化的粒子的维数n, n =K+N, K 和N 分别为ESN 输入和储备池神经元数量, 初始化 Xi和Vi, 对数据进行处理以确保数据的完整性.

Step 2.加载数据到输入输出, 更新 x(t), 使用Wiener-Hop f 的方法确定Wout.

Step 3.使用GTPSO 算法对 Wout进行选择, 得到Gbest, 即最优

Step 4.ESN 预测数据, 最终获得预测结果.

ESNGTP 算法流程图如图3 所示.

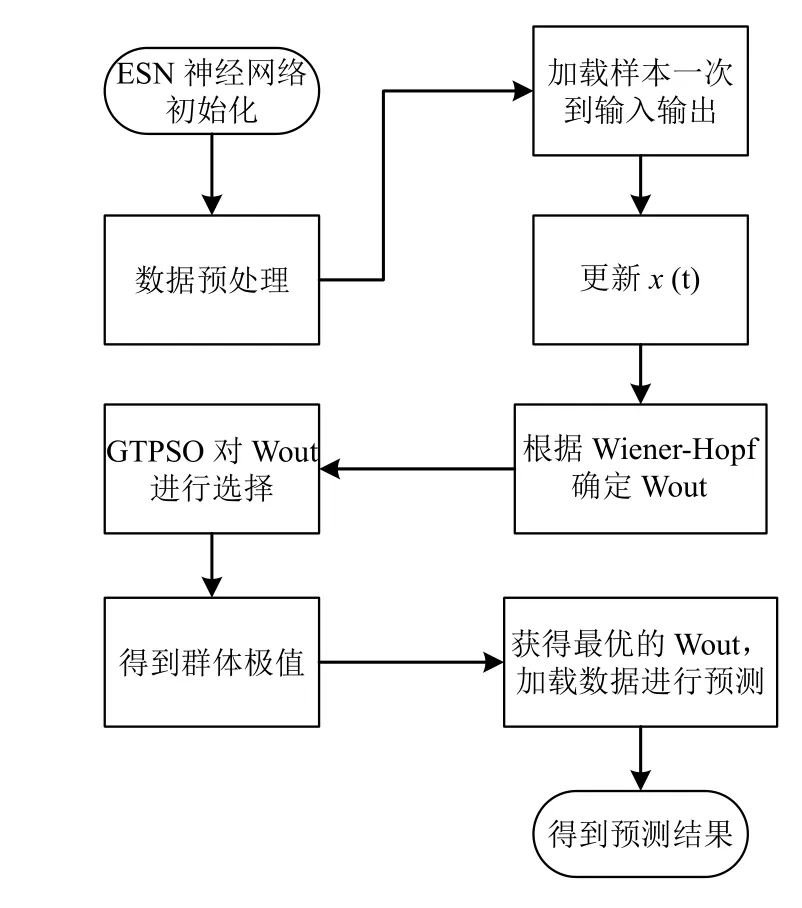
图3 ESNGTP 混合算法流程图

7 实验结果与分析

7.1 实验环境

实验计算机配置: CPU Core(TM)3.40 GHz, 内存16 GB, 显存8 GB; 操作系统: Windows7; 软件环境:Mtalab 2014.

7.2 实验数据获取

实验数据的数量一定程度上影响实验的预测效果,因此本文实验数据选取金螳螂(002018) 2012 至2018 年每日收盘价价格和中国石油(601857) 2013 至2019 年每日收盘价价格作为实验数据集.数据源来自于同花顺, 首先对数据进行手动清理, 将缺失的数据及当日收盘价为0 的数据进行清除, 选取两个个股的1152 天收盘价价格作为训练数据, 选取288 天收盘价价格作为测试数据.将前10 天的收盘价作为输入, 第11 天的收盘价作为输出.

7.3 评价标准

使用平均绝对误差(MAE)和平均绝对百分比误差(MAPE)对算法的优劣进行评估.MAE 越小, 预测值与真实值之间的误差越小.在同组数据下进行实验, 对比不同算法结果, MAPE 越小, 算法性能更优.

7.4 ESNGTP 算法预测结果与分析

建立ESN 模型, K, N, L 分别设置为10, 500, 1, 学习因子 c1 =c2=2, m =20, n =K+N, PSO 中粒子的Vi和 Xi在允许的范围内随机产生.本文将金螳螂(002018)和中国石油(601857)两支个股的每日收盘价作为实验数据, 金螳螂(002018)选取2012 年至2018 年1152 条数据作为训练数据, 选取288 条数据作为训练数据.中国石油(601857)选取2013 年至2019 年1152 条数据作为训练数据, 选取288 条数据作为训练数据.

分别采用BP、ESN、ESN-PSO 和ESNGTP 算法对数据进行训练, 同时针对训练好的模型带入实验数据进行测试, 其中金螳螂(002018)测试结果如图4 至图6 所示, 中国石油(601857)测试结果如图7 至图9所示.为了使图像效果更加清晰, 将ESNGTP 算法结果单独画出.对预测结果展开分析:

(1) 由图5 和图8 可知, ESN 的效果明显优于BP 的预测结果, 因为ESN 可以较好的寻找历史输入与输出之间的关系.

(2) 由图5 和图8 可知, 为了提高实验预测的精度,在接下来的实验中对ESN 的 Wout进行优化.ESNPSO 的效果优于ESN.

(3) 由图4、图6、图7 和图9 可知, 在个股收盘价的预测上, ESNGTP 相比于传统的ESN 更加精准,对抗局部收敛的能力较强, 达到了预期的效果.

图4 ESNGTP 预测结果与真实值对比

图5 3 种算法预测结果对比

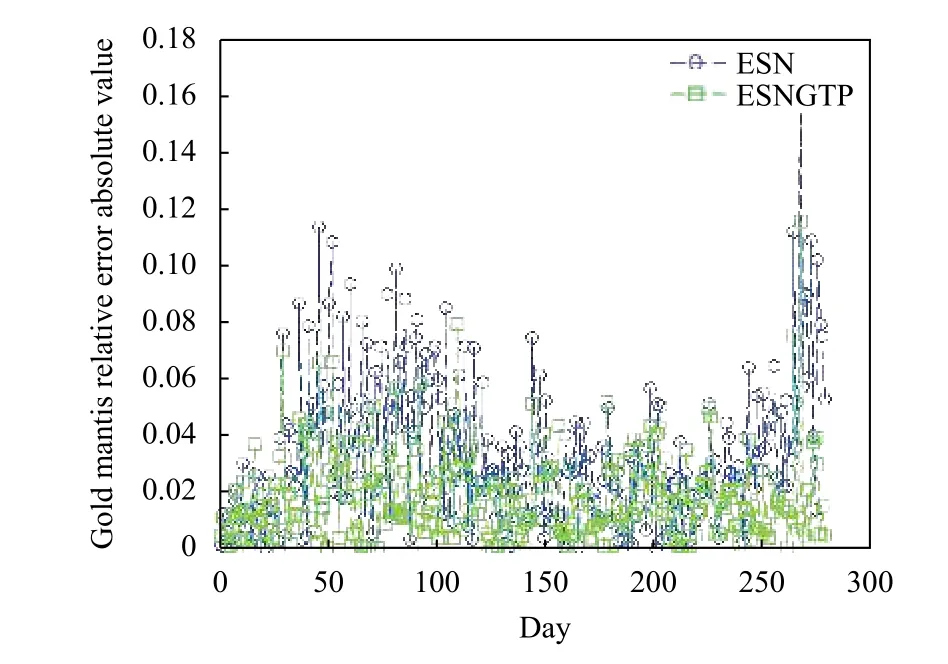
图6 ESNGTP 与ESN 相对误差绝对值对

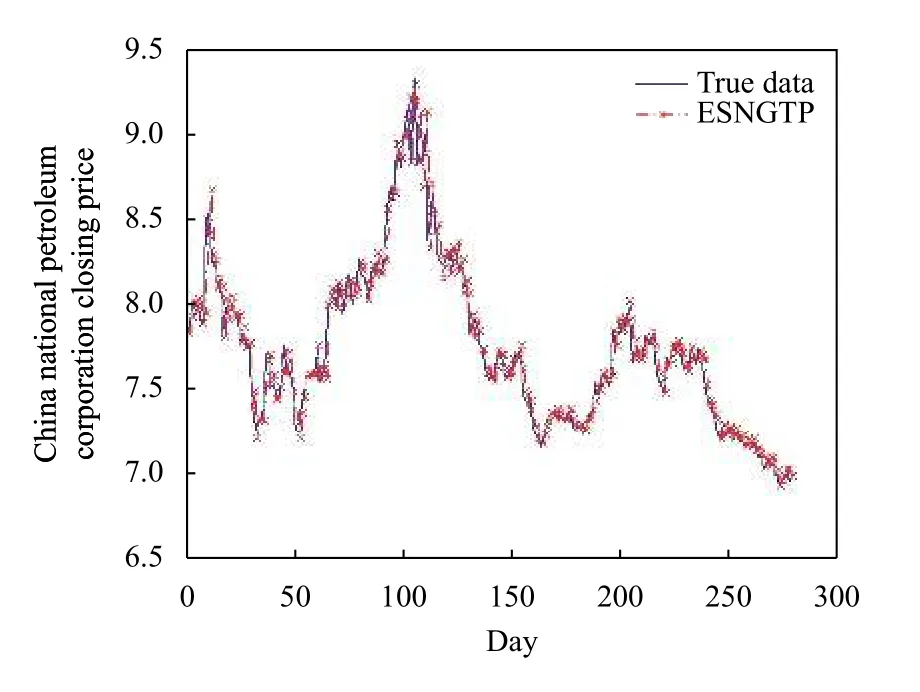
图7 图7 ESNGTP 预测结果与真实值对

将不同算法的预测结果进行分析, 结果如表1 所示.

从表1 可以看出ESN 效果明显优于BP, 而ESNPSO 预测效果优于ESN, 此外ESNGTP 算法的预测结果较好于传统的ESN 和ESN-PSO, 在ESNGTP 算法中, 预测精度得到提升, 解决了传统ESN 泛化能力不强的问题.

图8 3 种算法预测结果对比

表1 不同数据集下算法预测误差对比

8 结论

本文基于传统的ESN 预测模型, 使用GTPSO 算法完成对ESN 的 Wout的选择, 获得较优的 Wout, 进而使得预测更为精准.GTPSO 算法在传统的PSO 算法中上提出了两点创新, (1)引入GA 算法中变异的思想, 只有当粒子群聚集严重时才会发生变异, 重新初始化部分粒子, 扩大了PSO 算法搜索的范围, 增强了PSO 的全局搜寻能力, 同时可以保持较快的前期寻优速度.(2)引入TS 中禁忌的思想, TS 的局部寻优能力较强,搜索的过程中拥有记忆, 降低算法陷入局部最小值的状况.保持较快的后期寻优能力, 当PSO 陷入局部最优时, 可以通过禁忌逃离这种局部最优的状况.本文使用ESNGTP 算法对金螳螂(002018)和中国石油(601857)两支个股收盘价进行预测.通过实验说明ESNGTP 算法相比于传统的ESN, 预测效果更为精准.在迭代的过程中, 从表1 可知ESNGTP 相比于ESNPSO 有较好的收敛效果.

虽然引入的变异思想和禁忌思想提高了预测的精度, 但是在迭代的过程中消耗的时间稍长, 因此在时间上的消耗有待改进.此外, 实验中对于个股股价的预测使用的是每日收盘价的数据, 未曾考虑其他的影响因素, 下一步的工作, 需要考虑多种因素对收盘价的影响,同时依据影响因素重要性的不同, 给与不同的影响因素相适应的权重.