JWF1278型精梳机锡林壳体静力结构分析

吴云珍

（经纬智能纺织机械有限公司，山西 晋中 030601）

0 引言

新型JWF1278型精梳机围绕先进技术装备要求，在高速变速梳理技术、钳板传动结构、分离罗拉运动机构、牵伸技术机构等核心技术方面体现出了优良的设计和制造特点［1］。锡林壳体是精梳机圆梳部件上的重要零件，它通过两组螺栓联接抱紧在锡林轴上，随锡林轴一同做回转运动，从而带动锡林转动。经纬智能纺织机械有限公司JWF1278型精梳机锡林壳体采用压铸铝合金轻质材料，减少了组件的转动惯量，适应高速圆周变速运动，但是对加工和装配的精度提出了更高的要求。在安装锡林壳体时，螺栓的拧紧力矩非常关键，若拧紧力矩过大，会造成锡林壳体的变形损坏；若拧紧力矩过小，则可能会使锡林壳体与锡林轴在高速运行时出现相对滑动现象。为此，有必要对安装锡林壳体时所需的螺栓预紧力进行计算，得出比较合理的拧紧力矩值，为设计人员提供理论参考依据。而要计算出准确的螺栓预紧力，首先必须知道锡林壳体在工作状态下承受的最大扭矩，然后计算出锡林壳体所需的最大静摩擦力，接着由此计算出锡林壳体对锡林轴的最大正压力，最后计算出抱紧螺栓所需的预紧力大小。

本文通过计算得出JWF1278型精梳机锡林壳体抱紧力，估算锡林壳体抱轴的螺栓预紧力及拧紧力矩大小，在Creo 4.0软件中建立锡林壳体螺栓联接组件的三维模型，再导入ANSYS Workbench软件中对其进行静力结构分析。

1 锡林壳体的受力分析

JWF1278型精梳机圆梳部件主要由锡林轴、锡林、平衡板、锡林壳体组成，如图1所示。锡林轴共带动8组锡林壳体结合件运转，每组锡林壳体结合件包括2个锡林壳体、1个锡林、1个平衡板。其中，每个锡林壳体与锡林轴均由两组螺栓抱紧在一起。锡林轴转动时带动锡林转动，故锡林轴对锡林壳体的正向摩擦力是锡林壳体能转动起来的动力，也是使锡林壳体能转动的最小动力。若能算出此正向摩擦力值，便可以估算出锡林壳体所受的正压力，从而得到锡林壳体的抱紧力大小。

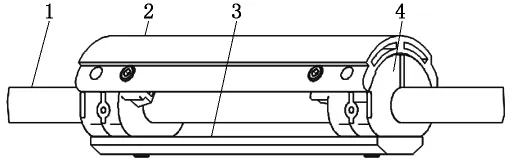
图1 JWF1278型精梳机圆梳部件

1.1 计算锡林轴最大角加速度

在Creo 4.0软件中分别对主动非圆齿轮与从动非圆齿轮进行敏感度分析，取最小分度为0.1°，则沿非圆齿轮一周有3 600个分度，以一对非圆齿轮分度圆上啮合的初始位置为起点，得到主动非圆齿轮和从动非圆齿轮旋转一周各分度的位移S1和S2，从而可以计算出一对非圆齿轮的传动比i＝S2／S1，再根据电机转速n及两级非圆齿轮的传动比计算出锡林轴在各分度的转速n1＝i2n，然后计算出锡林轴在各分度的角速度ω＝2πn1／60，最后计算锡林轴的角加速度α＝Δω／Δt（Δω为相邻两个分度角速度的变化值，Δω＝Δω（k＋1）－Δωk，k＝1，2，…，3 600，Δt为与转速n1相对应的时间间隔）。

取正常工况下S1＝39.043mm、S2＝48.183mm、n＝500r／min。计算得：i＝1.234 1，n1＝761.5r／min，ω＝79.7 rad／s，Δt＝60／（3 600n1）s，Δω＝0.049 7rad／s，则锡林轴的最大角加速度α＝Δω／Δt＝2 270.75rad／s2。

1.2 计算锡林壳体最大扭矩

在Creo 4.0软件中建立一组锡林壳体结合件的三维模型，测得其转动惯量J＝6.42×10－3kg·m2，则其转矩T1＝Jα＝6.42×10－3×2 270.75N·m＝14.58N·m。

根据设计人员提供的经验值，锡林轴在锡林梳理时承受的扭矩大约为M＝15N·m，因锡林轴同时带动8组锡林进行梳理，所以平均分配到每个锡林上的梳理力矩M′＝M／8＝1.875N·m。因锡林在梳理时还需克服梳理力矩的作用，则锡林壳体结合件在高速圆周变速运动时所承受的最大扭矩T2为其转矩与锡林上的梳理力矩之和，即T2＝T1＋M′＝16.455N·m。则分配到每个锡林壳体上的扭矩T＝T2／2＝8.23N·m。

1.3 计算锡林壳体的抱紧力

已知锡林轴半径r＝15mm，可以计算出锡林壳体所受正向摩擦力：

锡林壳体材料为YL112，锡林轴材料为55钢，锡林轴与锡林壳体之间的摩擦因数μ＝0.17［2］，则锡林壳体所受正压力为：

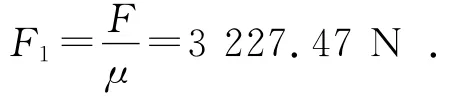
即锡林壳体对锡林轴的抱紧力为3 227.47N。

2 估算螺栓预紧力

首先需要估算锡林壳体抱紧力与螺栓预紧力的关系。现将锡林壳体受到的螺栓预紧力模型简化为力学模型，如图2所示。测得锡林壳体内侧曲面半径R＝15mm，锡林壳体轴心距螺栓中心距离为24.42mm。在螺栓预紧力F0作用下，锡林壳体抱紧力F1作用面其实是分布在锡林壳体整个内侧面。假设在螺栓预紧力作用下，锡林壳体还未发生变形，则锡林壳体抱紧力F1应发生在图2所示位置处。经测量图2所示夹角θ＝38°，则：

根据拧紧力矩T′≈0.2F0d［3］（d为螺栓的公称直径，d＝8mm）估算拧紧力矩：

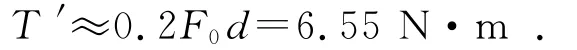
在这里取整值，即T′＝7N·m，故可以得出锡林壳体抱轴的螺栓联接拧紧力矩至少为7N·m。

3 锡林壳体静力结构分析

3.1 简化模型及设置材料属性

在Creo 4.0中建立锡林壳体螺栓联接组件的三维模型，简化螺栓、螺母的几何模型，确保零件之间没有干涉现象，简化后的锡林壳体螺栓联接组件三维模型如图3所示。将简化后的锡林壳体螺栓联接组件三维模型导入到ANSYS Workbench软件的静力结构分析模块（Static Structural）中进行分析。

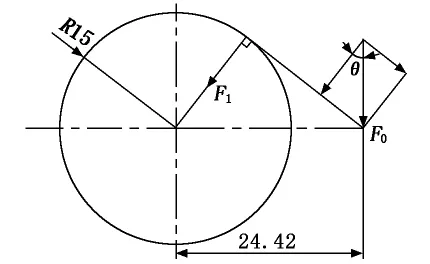
图2 锡林壳体抱紧力与螺栓预紧力关系简化模型

图3 锡林壳体螺栓联接组件三维模型

锡林壳体材料为YL112，螺栓螺母材料为不锈钢，它们的材料属性如表1所示［4］。

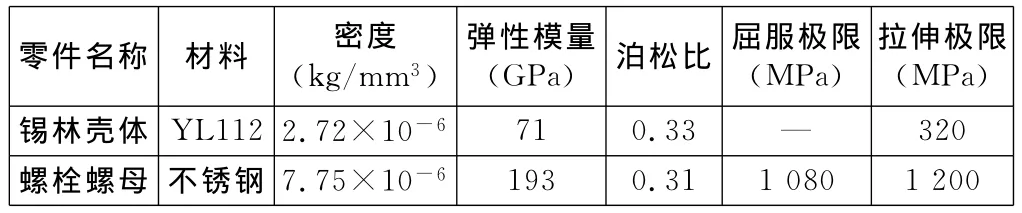
表1 零件材料及属性

3.2 设定接触类型和划分网格

在静力结构分析模块的机械模型（Mechanical）界面中，采用手动方式为锡林壳体、螺栓、螺母进行接触设置，将锡林壳体与螺栓、锡林壳体与螺母、螺栓与螺母之间的接触均设置为绑定（Bonded）连接。锡林壳体采用高阶的四面体网格（Tetrahedrons）划分生成四面体单元，设置其网格尺寸为3mm；螺栓和螺母采用多区网格（MultiZone）划分生成六面体单元，设置其网格尺寸为2mm。进行网格划分后，检查网格单元质量为0.76，网格倾斜度为0.33。查网格倾斜度质量评估表可知此网格划分单元质量较好［5］。

3.3 边界约束条件

正常工况下，锡林壳体随锡林轴在做高速圆周变速运动，选取锡林壳体在承受最大扭矩时的状态作为研究对象进行静力结构分析。假设锡林壳体与锡林轴之间无轴向滑动，也无相对转动，锡林壳体向外可以径向膨胀，所以在锡林壳体内侧与锡林轴抱紧的圆柱面上施加圆柱支撑约束（Cylindrical Support），设置轴向（Axial）和切向（Tangential）均为固定约束（Fixed），径向（Radial）为自由约束（Free）。施加旋转速度（Rotational Velocity），转速方向为锡林轴的旋转方向，转速n1＝761.5r／min。施加两组螺栓预紧力（Bolt Pretension），预紧力方向分别沿各自螺栓轴方向，预紧力F0＝4 095.72N。锡林壳体螺栓联接组件被施加约束和载荷后如图4所示，其中，A处施加圆柱支撑约束，B处施加转速，C处和D处分别施加螺栓预紧力。

图4 锡林壳体螺栓联接组件约束及载荷

3.4 静力分析结果

设置完成后，进行求解并查看分析结果。锡林壳体等效应力分布云图如图5所示，最大应力约为176.16 MPa，位置在锡林壳体内侧圆柱曲面的边上。锡林壳体总形变分布云图如图6所示，最大形变约为0.08mm，发生在壳体夹紧锡林轴的顶端开口处。

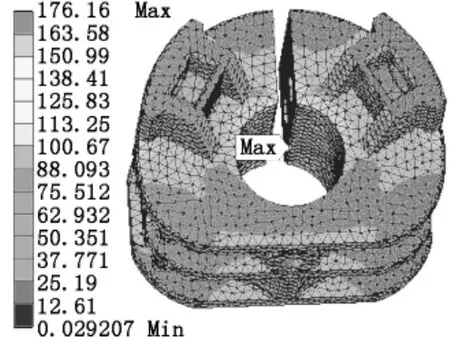
图5 锡林壳体等效应力分布云图

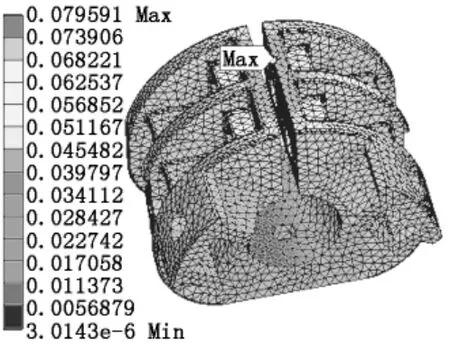
图6 锡林壳体总形变分布云图

因锡林壳体材料YL112属脆性材料，所以采用第一强度理论［6］来对分析结果进行评估。插入应力工具（Stress Tool）下的最大拉应力（Max Tensile Stress）理论，选择默认应力极限类型（Stress Limit Type）为材料的拉伸极限，通过评估计算得出锡林壳体的最小安全系数（Safety Factor）为3.07，如图7所示。由此最后得出结论，在此工况下锡林壳体的强度和刚度均满足要求，可以安全可靠地运转。

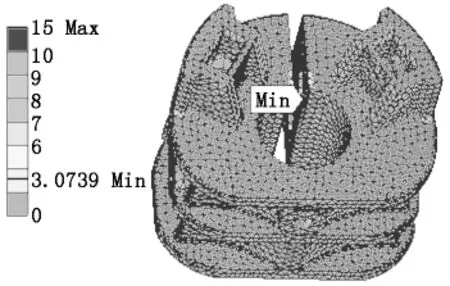
图7 锡林壳体安全系数分布云图

3.5 参数化分析

将锡林壳体螺栓联接组件边界约束条件中的两组螺栓预紧力设为输入参数，锡林壳体的最大应力、最大形变、最小安全系数设为输出参数。以预紧力大小4 095.72N为参考值，在参数设置（Parameter Set）中设置不同的输入参数值，再进行参数化分析，结果如表2所示。

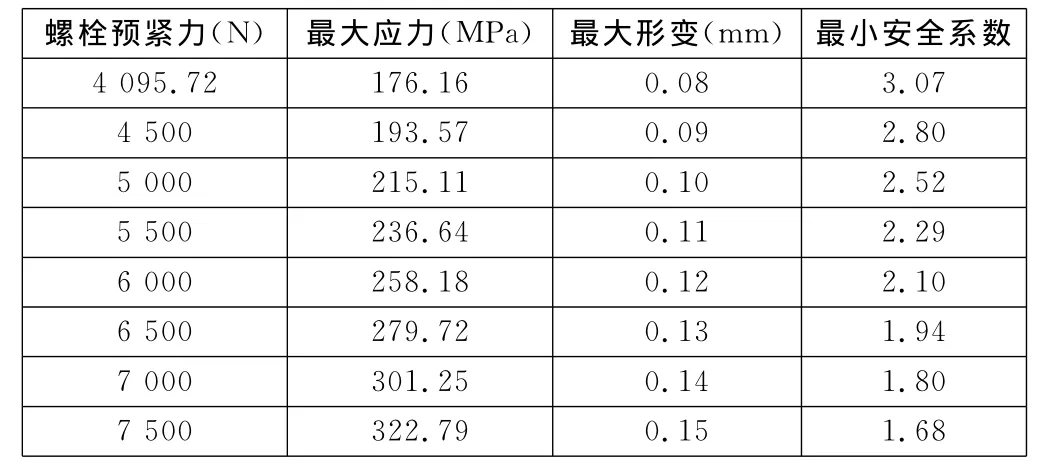
表2 参数化分析结果

由表2中可知，当螺栓预紧力增大至7 500N时，锡林壳体的最大应力已经超过了材料的拉伸极限，所以螺栓预紧力最大不能超过7 500N。再根据拧紧力矩公式估算最大拧紧力矩T′＝0.2F0d＝12N·m，故得出：锡林壳体抱轴的螺栓联接拧紧力矩至少为7N·m，最大不能大于12N·m。

4 结语

本文首先通过计算得出JWF1278型精梳机锡林壳体对锡林轴的抱紧力，并估算出锡林壳体上两组螺栓联接的预紧力及拧紧力矩大小，再对锡林壳体螺栓联接组件进行静力结构分析，得出如下结论：锡林壳体在承受最大扭矩工况下，其强度和刚度均满足要求，且能安全可靠地运行。最后对锡林壳体螺栓联接组件边界约束条件中的两组螺栓预紧力的大小进行参数化分析，得出合理的螺栓联接拧紧力矩范围，可为设计人员及装配人员提供理论参考。