基坑土石方几种体积计算公式的适用分析

成如刚

（黄冈职业技术学院 湖北 黄冈 438002）

在挖基础土石方工程量计算实践中，基坑平面形状和基坑形体越来越多样化，平面形状已经不再局限于矩形、圆形，基坑的形体也不再局限于柱体、梯形体或者棱台。面对这种情况，基坑土方体积计算公式该如何正确选择呢？我们有必要对各种基坑（含基础大开挖）土方形体体积计算公式的适用范围进行分析。

1 土方垂直开挖，不放坡时的体积计算

此情况下，无论是否支挡土板、留工作面，任意形状基坑均为柱体。

土方体积=坑底面积×挖深

1.1 任意形状基坑

设基坑底面面积为S，基础底面至设计室外标高深度为h，则：

1.2 矩形或方型基坑

设基坑底面尺寸为a×b，基础底面至设计室外标高深度为h，此时坑底面面积S=ab，则：

1.3 圆形基坑、桩孔

设基坑底面半径为r，基础底面至设计室外标高深度为h，坑底面面积S=πr2，则：

2 土方开挖需放坡时的体积计算

放坡后形成各种形体，如拟柱体、梯形体、棱台、圆台、球缺、棱柱、圆柱、长方体等。

2.1 拟柱体体积公式及适用范围

拟柱体是指所有的顶点都在两个平行平面内的多面体。其体积公式为万能公式，可计算初等几何里各种形体的体积。公式如下：

其中：S上-上底面积；S下-下底面积；S0-中截面面积；h-高。

如果S（x）是x不超过三次的多项式，就能用拟柱体公式计算这个物体的体积。（注：用平行于底面的平面来切割物体，x记为平面到下底的距离，S（x）记为这个平面截物体所得的剖面面积）。[1]

长方体、圆柱、棱柱、圆锥、棱锥、圆台、棱台、梯形体、球、球冠、球缺等尽管各有自己求体积的公式，但都是拟柱体的特例，都可以用拟柱体公式计算体积[1-2]。

一般情况下，对任意平面形状的基坑土方（含基础大开挖土方），均可按拟柱体体积公式计算土方。

2.2 棱台体积计算公式及适用范围

当拟柱体的上下底面是对应边平行的相似多边形时，它就是棱台。只要上、下平行的两个面的对应边比值相等，这两个面相似[3]。

在土方计算时，公式（5）仅适用于基坑底面为正方形、圆形，且周边放坡系数相等的情况。

当拟柱体的上下底面是对应边平行，但上下底面不是相似多边形时，就不是棱台，此时体积计算按万能公式h（S上+4S0+S下）计算，不能按公式（5）计算。

2.3 梯形体计算公式及适用范围

梯形体（如图1所示）是指上下底面平行且为平行四边形，四个侧面都是梯形的拟柱体，正四棱台是梯形体的特例。

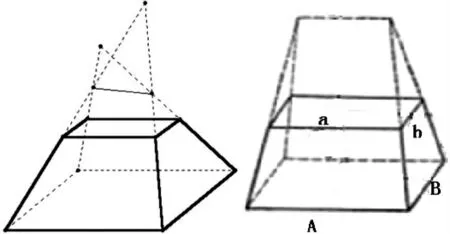
图1 梯形体

其中：两底为平行四边形，a、b、A、B分别为上下底边长；h为高。

正四棱台是梯形体的特例，正四棱台可采用梯形体体积公式计算，而梯形体体积不能采用正四棱台体积公式计算。

如何判断四棱台还是梯形体呢?只要上、下平行的两个面的对应边比值相等，这两个面相似，这时四个棱的延长线肯定交于一点，一定是四棱台，不然就是梯形体。[3]

梯形体体积公式（6）也可转换成另一体积公式：

如图2所示，若a=a′+2c，b=b′+2c；A=a+2kh，B=b+2kh。代入体积公式（6），发现公式（6）与公式（7）相等。即h[ab+（a+A）（b+B）+AB]=h（a+Kh）（b+Kh）+K2h3=h（a′+2C+Kh）（b′+2C+Kh）+K2h3

在土方计算时，梯形体体积公式（7）仅适用于基坑底面为矩形且四面放坡系数相等的情况。只要是梯形体，公式（6）均适用。但对平面是三角形或者梯形的情况，可以补上大小一样且互为对边的图形，形成矩形后也可适用公式（6）、（7），其体积计算结果取1/2即可，见图2。

2.4 多个矩形组合形状的基坑体积公式及适用范围

多个矩形组合形状的基坑土方（含基础大开挖）形体还是拟柱体，无论周边是否均匀放坡，均可按万能公式（4）计算。

对由多个矩形组合的平面，周边均匀放坡（放坡系数相等）时，也可以按如下公式[4]计算：

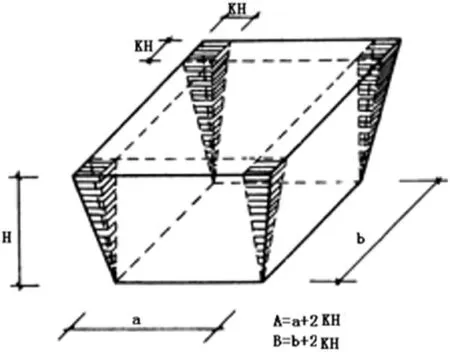
图2 方形放坡地坑（梯形体）

其中：S下-坑底面积；L-坑底周长；h-高；K-放坡系数。

多个矩形可以组合成L形、凹形、凸形、十字形、Z形等形状（见图3[4]）。

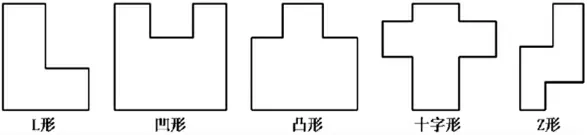
图3

对矩形组合的基坑，均适用拟柱体万能公式（4）。满足如下条件时，也可适用计算公式（8）：

①仅当周边均匀放坡（放坡系数相等）时适用。若四周放坡不均匀，则只能适用拟柱体万能公式（4）。

②对转角处均为900的凹凸形等基坑平面，周边均匀放坡时，适用公式（8）。否则，只能适用拟柱体万能公式（4）。

③对于转角处均为900的回形基坑平面，公式（8）不适用。只能适用拟柱体万能公式（4）。

④对于有≠900转角（含弧形）的基坑平面，公式（8）不适用。只能适用拟柱体万能公式（4）。

3 实例计算比较

3.1 四棱台与梯形体公式应用比较

背景资料：某工程挖矩形基坑，坑底长为7.0m，宽为4.0m，四周放坡系数0.5，深度为2.0m，三类土。计算挖基坑土方工程量。

计算过程：

基坑底a=7m，b=4m；基坑顶A=5+0.5×2×2=9m，B=4+0.5×2×2=6m

本基坑不是棱台而是梯形体（判断条件a：A=7/9=0.778≠b：B=4/6=0.667，不是棱台）。

应用梯形体公式（6）计算：

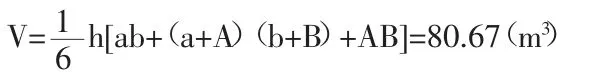
若应用棱台公式（5）计算，则结果有误差，过程如下：

S上=9×6=54（m2），S下=7×4=28（m2）

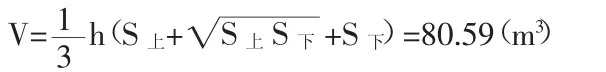
二者结果差率=（80.59-80.67）/80.67=0.1%。上下面对应边比值越不相近，差值越大[3]。

3.2 矩形组合坑体计算公式应用比较

背景资料：某大基坑底平面尺寸见图4，坑深5.5m，四边均按1：0.4的坡度放坡，计算基坑开挖的土方量。

计算过程：

方法一，利用万能公式（4）计算：

该基坑每侧边坡放坡宽度为：Kh=0.4×5.5＝2.2m；坑底面积为：S下＝30×15－10×5＝400m2；坑口面积为：S上＝（30+2×2.2）×（15+2×2.2）-（10－2×2.2）×5＝34.4×19.4-5.6×5=639.36m2。

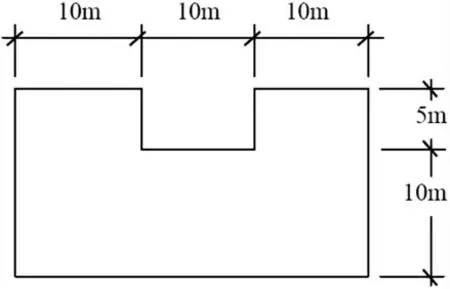
图4 基坑底面布置

坑口面平面计算的另一方法：坑口面平面相当于下底面外放kh宽所围成的平面，所以坑口平面面积也可按下式计算：S上=S下+下底周长×kh+4×kh×kh，下底周长L=100m，S上=400+100×2.2+4×2.2×2.2=639.36m2。

方法二，利用公式（8）计算：

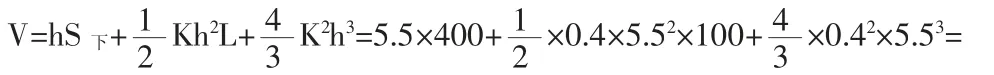
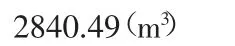
二种方法计算结果一致。

4 结束语

一般情况下，无论哪种平面形状的基坑，无论是否放坡，无论周边放坡是否均匀，土石方体积计算均适用拟柱体体积万能公式（4）。

对于平面为四边形的基坑，土石方体积计算还可适用梯形体体积计算公式（6）。四周放坡一致时还可适用公式（7）。正四棱台是梯形体的特例。

对于平面为矩形组合的基坑，若四周放坡均匀，土石方体积计算除适用拟柱体体积万能公式（4）外，还可适用计算公式（8）和（7）。

把握以上几点，对实践工作中正确选择基坑土石方的体积计算公式具有非常重要的意义。