非对称风场对台风浪模拟效果的比较研究
2020-03-21吴彦赵红军叶荣辉孙杰孔俊
吴彦,赵红军,叶荣辉,孙杰,孔俊
(1.江苏省海岸海洋资源开发与环境安全重点实验室河海大学,江苏南京210098;2.珠江水利委员会珠江水利科学研究院,广东广州510611)
1 引言
台风是发生在热带、亚热带海面上的气旋性环流,是地球物理环境中最具破坏性的天气系统之一。全球性气候变化的加剧以及沿海人口的增加,使台风对沿海地区社会财产和公共安全的威胁越发突显[1-2]。
由于初始条件和边界条件缺乏精度,采用原始方程对台风气压场和风场进行计算会遇到诸多问题[3],因此简单高效的参数化台风场模型一直有着较为广泛的应用。从台风场的构建思路上看,人们常利用圆对称的气压场模型(如Myers[4]、Jelesnianski[5]、Holland[6]等),根据旋恒风原理求解梯度风,然后再与移行风叠加合成台风场。该方法可考虑因环境气流引导造成的台风场的非对称,然而因下垫面、科氏力、环境气温等多种因素的影响[7],实际台风的非对称性更为复杂。各气象产品和各飓风中心网站发布的资料都显示台风具有非对称性:如图1所示美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)卫星和产品运营办公室发布的1330号台风“海燕”11月08日01:30分(世界时,下同)的卫星图像、以及表1所示的美国国家飓风中心(National Hurricane Center,NHC)发布的台风“Isabel”某一时刻的风场特征信息。笔者对联合台风警报中心(Joint Typhoon Warning Center,JTWC)发布的2004—2017年间的4个象限的台风半径数据进行了统计,结果显示台风在各个象限具有不同的尺度,其中东北象限和西南象限具有较强的非对称性(见图2)。
作为驱动因子,风场对台风浪的模拟起到重要的作用,随着对台风浪预报、后报精度要求的不断提高,构造更精准的台风风场模型成为一个重要的研究课题。本文将引入一个基于Holland模型改进的四象限非对称风场模型;又将Holland风场模型与移行风场模型叠加,构成一个只考虑移行作用下的叠加风场模型。参考JTWC发布的34KT、50KT、64KT下四象限的风速半径资料,模拟0814号台风“黑格比”的风场分布,比较这两种非对称风场的精度。采用两种非对称风场分别驱动第三代海浪模式SWAN(Simulating WAves Nearshore),对影响南海海域的3场台风(0814号台风“黑格比”、1329号台风“罗莎”、1409号台风“威马逊”)进行台风浪的数值模拟,对比分析了非对称风场关于南海台风浪的数值计算效果。

表1 2009年9月18日00时台风“Isabel”的风场特征信息

图1 1330号台风“海燕”的卫星图像(引自https://www.noaa.gov/)
2 台风风场模型
2.1 Holland风场模型
Holland圆对称气压场模型[6]的表达式为

式中:P(r)为距台风中心r处的气压值;r为距台风中心的距离;Pc为台风中心气压;Pn为外围环境气压;Rmax为某一时刻台风的最大风速半径;B为台风轮廓参数,Vickery等[8]、林伟等[9]分别对B值进行了研究,计算式如下:

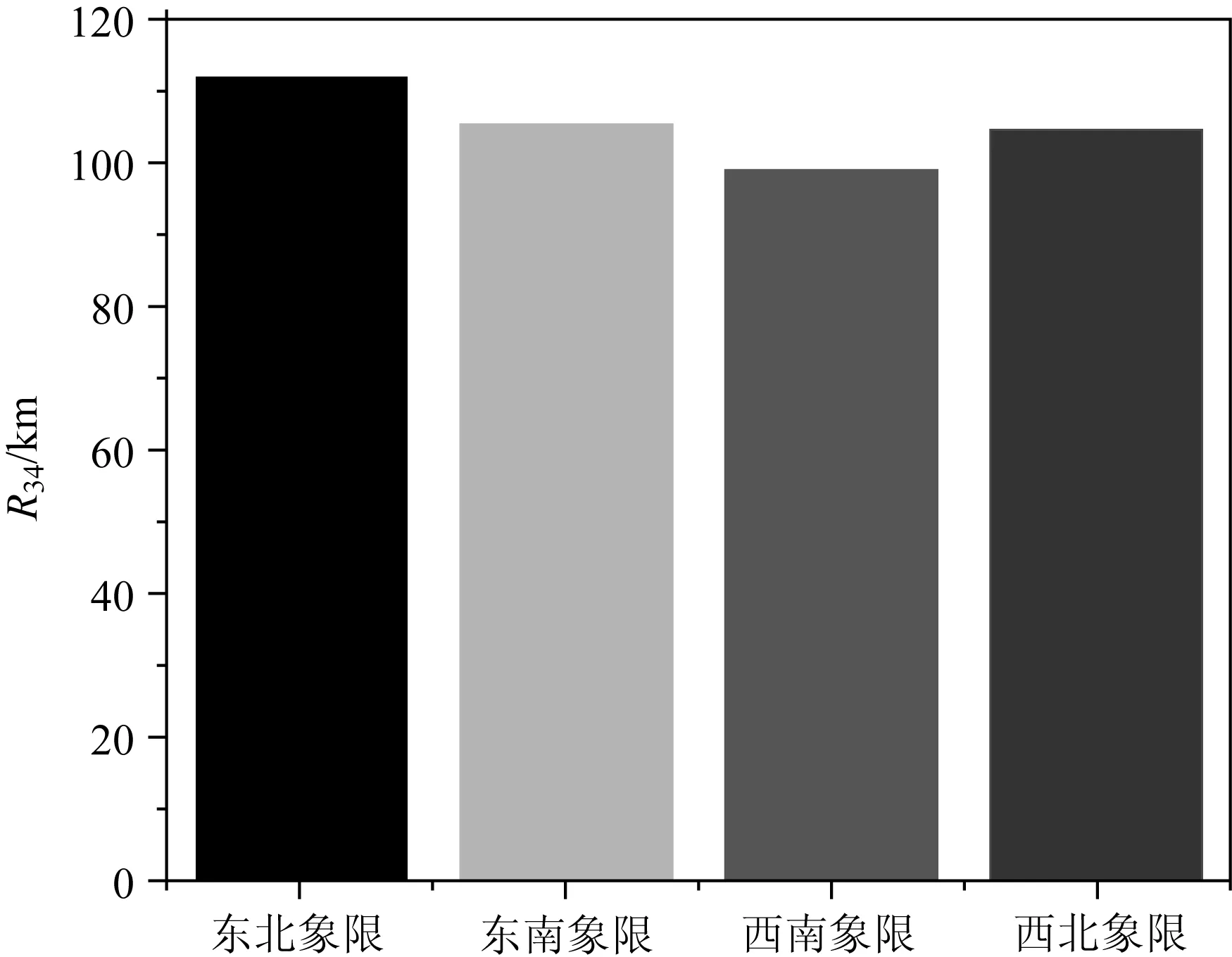
图2 西北太平洋4个象限台风尺度
式中:Vmax为某一时刻台风的最大风速;ρ为空气密度;e为自然对数,取为2.718 3。
基于气压场分布,利用旋恒风原理,得到梯度风的计算公式,如下

式中:V(r)为距台风中心r处的切向风速;f为科氏力。
2.2 非对称风场模型
由于实际的台风往往是非对称的,为了更好地描述实际风场,各国学者相继提出了各类非对称风场模型。以往的非对称风场模型只考虑台风移行对非对称的影响,即将对称风场模型与移行风场模型叠加。台风移行风场可采用宫崎正卫[10]模式,其风速表达式为

式中:Vt为台风移行速度;Vf为台风中心移行速度;RG为环境尺度,本文取500 km。
将台风的梯度风场与移行风场合成,得到台风风场

式中:V为叠加风场的风速;c1、c2为修正系数,本文分别取0.9和0.5;θ为计算点与台风中心连线与x轴的夹角;β为梯度风与海面风的夹角,本文取25°。
实际上台风的非对称受台风中心气压、边界层、台风登陆等多种因素[7]的影响。因此Xie等[11]利用气象中心发布的台风数据,提出了一种基于Holland模型的四象限非对称风场模型。该模型考虑了最大风速半径Rmax之于方位角的变化,表达如下:
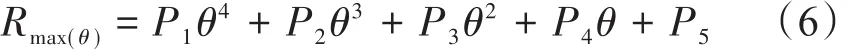
式中:Rmax(θ)为最大风速半径,P1、P2、P3、P4和P5为待定系数,计算方法如下:首先依据已发布的台风在某一时刻同一风速下的4个象限(东北、东南、西南、西北)风速半径,采用式(3)计算4个象限的最大风速半径;然后把计算所得4个象限的最大风速半径代入式(6),通过最小二乘法拟合求解系数P1~P5。
将求得的各个方位的Rmax(θ)代入下式中即可得到四象限非对称风场V(r,θ):

式中:Rˉmax为最大风速半径平均值,因各个方位的Rmax(θ)不同,所以计算出的风场是非对称的。
3 风场风速验证
为验证两种非对称风场的精度,以0814号台风“黑格比”为个例,对两种非对称风场的数值结果进行对比分析。台风“黑格比”某一段时间内的台风信息如表2所示,移动路径如图3所示。“黑格比”于9月22日18点—9月23日12点这一段时间内的台风资料显示,其具有明显的非对称性,其中东北、西北象限的风速半径相同且明显大于东南、西南象限的风速半径。验证风速测站点如图3所示,包括闸坡测站、珠海测站、珠江口外海测站和汕尾测站。将两个非对称风场进行编号:对称风场与移行风场叠加形成的叠加风场为风场1、基于Holland模型改进的四象限非对称风场为风场2。风速的验证结果如图4所示。

表2 台风“黑格比”一段时间内的风场特征信息

图3 台风路径及验证测点分布
从图4的验证结果可以看出,四象限非对称风场对风速的计算值与观测结果较为一致,尤其是当台风中心距离测站较近时,如台风“黑格比”珠海测站9月24日01:00时刻、珠江口外海测站9月23日11:00时刻以及汕尾测站9月23日19:00时刻。且四象限非对称风场模拟的风速与测站实测风速的相位更吻合,如台风“黑格比”闸坡测站、珠海测站。两种风场的风速均方根误差如表3所示:叠加风场在所有测站的预测风速均方根误差的均值为6.02 m/s,而四象限非对称风场在所有测站的预测风速均方根误差的均值为3.83 m/s,相对于叠加风场改进了2.19 m/s,提高了38.84%的计算精度。可见四象限非对称风场模型明显提高了风速的计算精度,尤其是对于台风大风区而言具有更好的模拟效果。

表3 风速均方根误差(单位:m/s)
4 台风浪数值计算
4.1 SWAN数值模式
第三代海浪模型SWAN[12-13]基于二维波作用量平衡方程建立模型,考虑了波浪破碎、风能输入、水底摩阻、波浪非线性相互作用等的影响,控制方程如下:

图4 台风“黑格比”风速验证
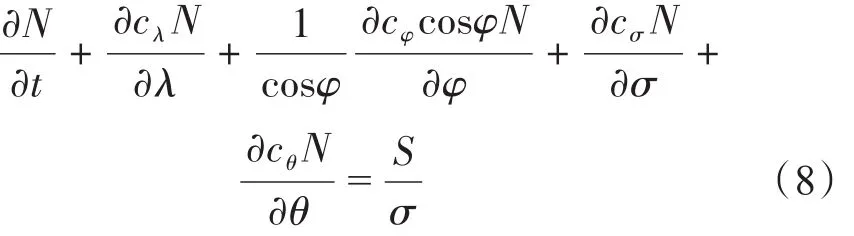
式中:N为波作用量密度;t为时间;λ、φ分别为经度和纬度;σ为相对频率;θ为传播方向;cλ、cφ和cθ为作用量在地理空间和谱空间上的传播速度;S为非保守源汇项。
4.2 模型设置
模型计算采用球坐标系下的非定常模式。在对计算域的空间范围和网格数进行敏感性分析后,取模型的空间计算范围为:15°~25°N,105°~125°E,如图5所示;采用矩形网格,网格数设置为301×601,空间分辨率为2′×2′;在二维谱空间上,频率的计算范围为0.03~1.0 Hz,以指数分布划分为36个,方向分段为36;时间步长设置为10 min。输入模型风场的空间分辨率设置为2′×2′,时间步长设置为1 h。模型计算的地形数据采用ETOPO1全球地形数据。
4.3 台风浪验证
为验证叠加风场和四象限非对称风场对台风浪的数值模拟效果,分别用叠加风场模型和四象限非对称风场模型驱动第三代海浪模式SWAN,对0814号台风“黑格比”、1329号台风“罗莎”、1409号台风“威马逊”3场台风进行台风浪的数值模拟,并与波浪观测站的实测值进行比较。上述3场台风的基本信息和计算时段见表4,路径和测站位置如图5所示,波浪实测资料包括阳西测站和珠江口外海测站。将两个非对称风场进行编号:对称风场与移行风场叠加形成的叠加风场为风场1、基于Holland模型改进的四象限非对称风场为风场2。
图6所示为四象限非对称风场和叠加风场模拟的有效波高与实测波高的比较,误差分析见表5。结果显示,总体上四象限非对称风场的模拟效果比叠加风场好,对波高时间变化过程的模拟效果较叠加风场有明显的改善。其中四象限非对称风场模拟出的波高峰值精度明显优于叠加风场,如台风“黑格比”珠江口外海测点9月23日21:00时刻、台风“威马逊”阳西测点7月18日17:00时刻。四象限非对称风场也能更好地模拟出极值有效波高的发生时刻,如台风“罗莎”阳西测站、台风“威马逊”阳西测站。误差分析显示叠加风场模拟出的有效波高均方根误差均值为0.83 m,而四象限非对称风场模拟出的有效波高均方根误差均值为0.70 m,比叠加风场减小了0.13 m,提高了28.58%的台风浪计算精度。由此可见四象限非对称风场可更好地模拟台风浪的时间发展过程,可提高台风浪的计算精度。

表4 样本台风基本信息

图5 台风路径及验证测点分布

图6 台风波高验证

表5 有效波高均方根误差(单位:m)
5 结论
本文分别采用叠加风场模型和四象限非对称风场模型构造风场,对0814号台风“黑格比”进行模拟,并将模拟风场与测站实测风场进行比较。分别采用上述两种风场驱动第三代海浪模式SWAN,对影响南海区域的3场台风(0814号“黑格比”、1329号“罗莎”、1409号“威马逊”)进行了台风浪的数值模拟,并与测站的实测波高进行了比较,得到以下结论:
(1)四象限非对称风场模型关于台风大风区的模拟优于叠加风场模型,其关于最大风速以及风速时间变化过程的预测更为合理;
(2)波浪数值模拟结果显示:四象限非对称风场对台风浪的模拟效果较叠加风场有所改善:有效波高模拟值与观测值的时间发展过程相吻合,且峰值波高的计算精度较高。
