一种利用浮标站资料改进海浪模式有效波高预报的方法

龚，曹宗元，刘菡，范其平，傅娜

（浙江省舟山市气象局，浙江舟山316021）

1 引言

灾害性海浪对海上安全威胁极大，根据历年海损事故的统计分析，造成的海损事故的原因中，海浪的影响非常大。仅2014年，舟山海域和渔场就有6艘渔（货）船因灾害性海浪而沉没。因此，提高海浪预报的准确率对保障广大渔民的生命、财产安全有着十分重要的现实意义。目前应用于海洋预报业务中的海浪预报方法主要有3种[1-4]：一是半经验半理论预报方法，主要有有效波预报方法[5]、PNJ波谱预报方法[6]和能量平衡导出谱预报方法[7]。二是经验统计预报方法，即通过经验统计方法建立风与海浪波高之间的预报模型来外推预报未来的海浪波高。常用的统计方法有多元回归，神经网络、卡尔曼滤波等[8-10]。半经验半理论预报方法和经验统计预报方法具有计算量小，实际应用方便的特点。三是数值模式预报方法。WAVEWATCHⅢ、WAM和SWAN（Simulating Waves Nearshore）等第三代海浪模式经过不断完善，已能较清晰地描述海浪的生消、传播及波波相互作用等物理过程，有着较高的预报准确率和较长的预报时效，成为当今海浪预报业务的应用发展方向[11-14]。然而，海浪生消、传播及波波相互作用等物理过程非常复杂，数值预报模式对其的描述存在局限性[15]。此外，数值模式本身的系统误差和外强迫场误差也制约着海浪预报的准确度[16]。Reikard等[17]通过对SWAN模式和统计模型的预报性能的比较，给出了数值模式和统计模型各自的预报性能优势。朱智慧等[18]发现建立WAVEWATCHⅢ模式的预报产品的统计预报模型，能提高其准确率。因此，本文将结合数值模式和统计模型的各自优势，利用浮标站海浪历史数据建立数值模式产品的订正统计模型，以期提高舟山渔场海浪预报准确率。

2 资料

本文所使用的资料有两类，具体如下：

2.1 海浪模式简介及其资料

舟山市气象局业务运行的海浪预报数值模式（简称ZS_WWⅢ-SWAN模式）是采用WAVEWATCHⅢ模式和SWAN模式嵌套运行，WAVEWATCHⅢ模式单向提供SWAN模式嵌套波谱边界条件。模式主要物理过程包括风浪相互作用、耗散、波波相互作用、底摩擦作用等。WAVEWATCHⅢ模式和SWAN模式的计算区域如图1中Ⅰ区和Ⅱ区所示，格距分别为10′和3′。模式输入风场采用GFS风场资料。两种模式均由初始时刻的海面风场和JONSWAP谱初始化。业务使用时采用6～72 h的模式预报产品。

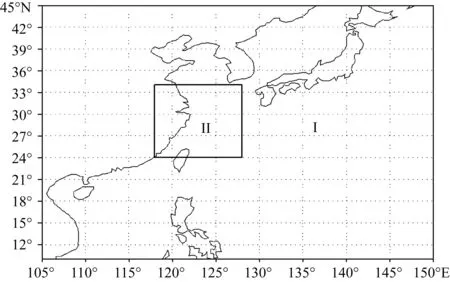
图1 ZS_WWⅢ-SWAN模式计算区域示意图

本文采用ZS_WWⅢ-SWAN模式中SWAN模式嵌套区域预报初始时刻为02时（北京时，下同）、08时、14时、20时的1～72 h有效波高预报数据。数据时段为2013年5月23日—2016年12月31日。在本文的分析中，将模式格点数据内插至舟山海洋气象浮标站站点位置（29°45′N，122°45′E）以代表该站点的有效波高预报值。

2.2 浮标站观测资料

本文研究中采用其对应2.1节中模式预报时刻的舟山海洋气象浮标站有效波高观测数据，资料时段为2013年5月23日—2016年12月31日，时间分辨率为1 h。

剔除缺测数据和有误数据，本文得到样本数351 504个。

3 方法

本文研究采用的回归分析方法为：设y为舟山海洋浮标站有效波高值，x为ZS_WWⅢ-SWAN海浪模式有效波高预报值，x，y的关系由一元n次回归方程确定，即：

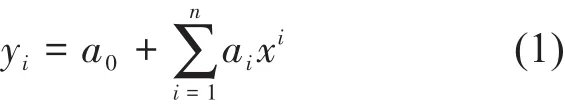
式中：n=1或2，即建立y和x的一元一次、一元二次回归方程。

4 订正预报模型的建立

根据式（1），对x和y进行回归分析，可建立ZS_WWⅢ-SWAN海浪模式1～72 h的逐小时预报有效波高的一元一次线性回归方程和一元二次回归方程，即得到上述二类回归方程各72个。

为了对比分析一元一次线性回归方程和一元二次回归方程的拟合效果，本文还计算了拟合有效波高和实测有效波高之间的误差均方根和相关系数（见图2）。由图2可知，这些回归方程的相关系数均大于0.67，误差均方根小于0.53 m，因此都有着较好的拟合效果。同时，图2a还显示，一元二次回归方程的误差均方根总体上小于一元一次线性回归方程的误差均方根，但随着预报时效的增长而二者差距不断减小。具体表现为：在1～15 h的预报时效内，一元二次回归方程的误差均方根与一元一次线性回归方程的误差均方根差距较为明显，15 h后差别变得不明显。从相关系数看（见图2b），在1～15 h的预报时效内，一元二次回归方程的相关系数比一元一次回归方程的相关系数偏大较为明显，15 h后随着预报时效的增长而二者差距逐渐变得不明显。

上述分析表明，就总体而言，一元二次回归方程比一元一次回归方程的拟合效果要好，因此在海浪预报业务应用中选取该方程作为订正预报模型。

5 业务应用检验

本文将一元二次回归方程作为ZS_WWⅢ-SWAN模式有效波高预报场的订正方程投入业务试运行，并对2017年7月1日—2018年10月10日（其中2017年10月28日—2018年1月14日因舟山浮标站维修而缺测）期间的业务试运行结果进行了检验。

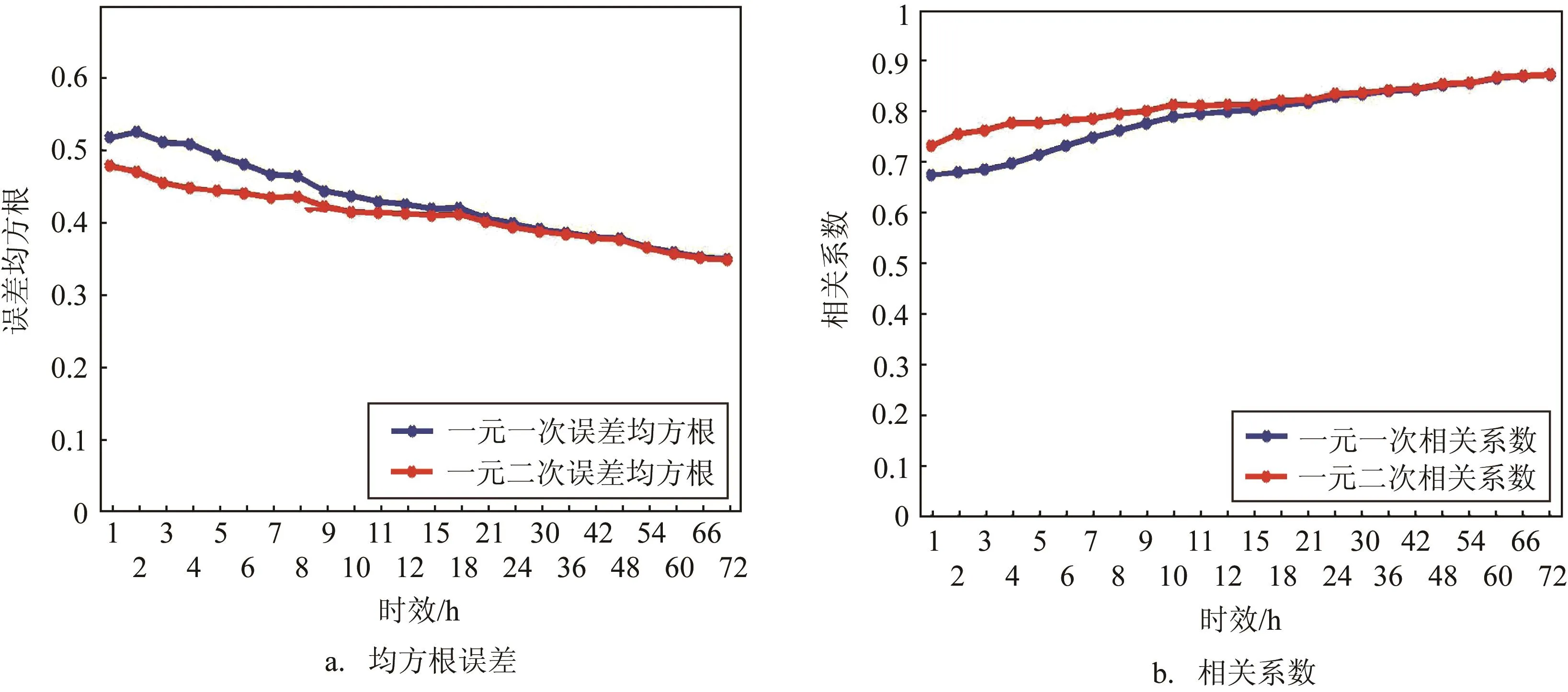
图2 两种回归订正方程对有效波高和实测有效波高拟合效果图

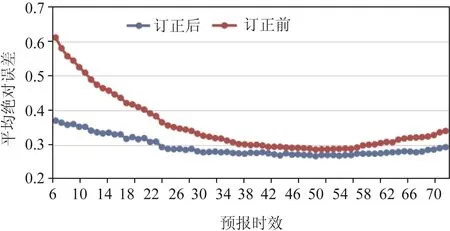
图3 2017年7月1日—2018年10月10日期间订正前后6～72 h的逐小时有效波高预报值和浮标站观测值之间的平均绝对误差

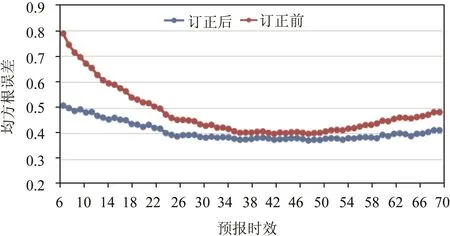
图4 2017年7月1日—2018年10月10日期间订正前后6～72 h的逐小时有效波高预报值和浮标站观测值之间的均方根误差

图3 给出了2017年7月1日—2018年10月10日期间订正前后6—72 h的逐小时有效波高预报值和浮标站观测值之间的平均绝对误差情况。由于ZS_WWⅢ-SWAN模式采用冷启动运行，模式运行前期不稳定，导致预报误差较大，第6～11 h有效波高模式预报值和浮标站观测值之间的平均绝对误差值为0.509～0.611 m，订正后平均绝对误差降至0.352～0.37 m。此后随着预报时效延长，模式平均绝对误差逐渐减小，从第12 h起降至0.5 m以下。39～59 h预报时效内平均绝对误差值介于0.286～0.3m之间。60～72 h误差略有上升，由0.301 m升至0.34 m。相对应的订正后的平均绝对误差为：第12 h起就降至0.341 m以下。39～59 h预报时效内平均绝对误差值介于0.269～0.278 m之间。60～72 h误差略有上升，由0.274 m升至0.293 m。以上分析可知，第6～11 h预报时效内模式预报误差较大，订正方程可有效减小模式系统误差，订正后有效波高的预报精度改善效果较明显，且预报时效越短订正效果越好，订正前后平均绝对误差减小值在0.17～0.241 m之间。其后随着预报时效的延长，模式的系统误差逐渐减小，订正方程的订正能力也逐渐降低。12～30 h预报时效内订正后平均绝对误差减小幅度在0.051～0.148 m之间。31～72 h预报时效内订正后平均绝对误差减小幅度在0.017～0.048 m之间。

就均方根误差检验而言，图4也反映出订正方程较好的订正能力。第6 h预报订正前后均方根误差减小幅度达0.28 m，在18 h内订正前后均方根误差减小幅度随着预报时效的延长逐渐降至0.103 m。19～29 h订正后均方根误差减小幅度在0.053～0.097 m之间。30～64 h订正后平均均方根误差减小幅度在0.022～0.049 m之间。65～72 h订正后均方根误差减小幅度在0.055～0.07 m之间。

6 结论

本文基于浮标站海浪历史数据，利用回归分析方法分别建立了海浪数值模式有效波高预报产品的一元二次回归订正方程和一元一次回归订正方程，对比分析误差均方根和相关系数发现，一元二次回归订正方程的拟合效果更好。将其作为订正统计模型并投入日常预报业务试运行后，2017年7月1日—2018年10月10日期间业务试运行结果显示，订正方程有较高的预报能力，能有效改善有效波高数值预报产品的预报精度，且预报时效越短订正效果越显著。第6～11 h预报时效内的订正前后平均绝对误差值减小0.17～0.241 m，第6～18 h预报时效内订正前后均方根误差减小幅度为0.103～0.28 m。这说明应用订正统计模型对海浪模式输出产品进行订正是不修改模式的情况下，改进海浪模式预报产品准确率的一种有效途径。