一种卫星微角振动高精度测量方法

吴文韬 李醒飞 刘帆 徐冲柯

(天津大学精密测试技术及仪器国家重点实验室，天津 300072)

高分辨率遥感卫星在轨时，活动部件或外界环境动力会产生微振动，其中的微角振动对卫星影响较大。卫星微角振动主要表现为稳态正弦响应、衰减振荡的角度抖动等，频率为0.1～1000 Hz，幅值在几十μrad到0.05 μrad之间[1]，具有幅值小、频带宽的特点。微角振动来源主要有以下几种：①太阳帆板、对地相机等部件运行；②变轨调姿期间推力器点火工作；③动量轮高速转动；④太空尘埃与卫星碰撞等。以上来源产生的微角振动会对相机图像的分辨率以及定向瞄准精度等造成较大影响，成为限制高精度卫星姿态控制精度和稳定性的一个主要因素。因此，准确、实时地对卫星结构微角振动进行测量，并对微角振动情况进行分析和补偿控制，在航空航天领域具有重要意义[2-4]。

目前用于微角振动测量的方法主要有：①基于光学平台的激光仪表测量方法[5]；②多个振动加速度传感器组合测量方法[6]；③基于光纤陀螺的测量方法[7]；④基于磁流体动力学(Magnetohydrodynamics, MHD)微角振动传感器(后文简称为MHD传感器)的测量方法[1]。激光仪表测量方法精度高，但系统组成复杂，仪表尺寸大，不适用于卫星在轨微角振动测量。振动加速度传感器组合测量方法体积小、成本低，但多个传感器组合后会引入误差源，精度不高，同时微角振动解算过程复杂，导致处理器功耗上升。光纤陀螺测量方法具有高动态、高灵敏度的特点，但带宽相对较窄、高频特性较差。MHD传感器测量方法的测量带宽可达1000 Hz，噪声等效幅值小于35 nrad[2]，且MHD传感器具有体积小、质量轻、易安装的特点，能够实时准确反映所测微角振动信息。

国外对MHD传感器的研究较早，并已开发出相对成熟的测量系统。其中，美国应用技术联合体(Applied Technology Associates，ATA)公司研发的MHD传感器[8]已用于地球静止环境业务卫星-N(GOES-N)的成像仪和X射线探测器[9]、先进陆地观测卫星(ALOS)的立体测绘仪[10]等结构的微角振动测量。我国对MHD传感器的研究起步较晚，发展较慢[11-13]，但研究日渐成熟，现已缩小与国外的差距。本文作者所在课题组已研制出多代MHD传感器样机，具备进行卫星结构微角振动高精度测量方法设计研究的能力。

本文根据卫星微角振动幅值小、频带宽的特点，以及卫星在轨微角振动测量系统轻质量、低功耗的需求，选用MHD微角振动传感器作为敏感元件，提出一种微角振动高精度测量方法，并通过仿真和试验验证了其可行性。

1 MHD传感器卫星微角振动测量方法

本文主要针对动量轮转动不平衡引起的对地观测卫星有效载荷微角振动进行测量，其频率范围为10～200 Hz，幅值范围为5～100 μrad[7]。

MHD传感器卫星微角振动测量原理图如图1所示。动量轮工作时产生微角振动并传递给有效载荷。MHD传感器与有效载荷通过机械固连进行微角振动传递，输出的微角振动模拟信号通过屏蔽缆线传入模数(AD)转换模拟输入端。经过AD转换后，数字信号采用差分方式传输，传输完成后，通过电平转换电路，将信号转化为晶体管-晶体管逻辑(TTL)电平形式。微控制器读取信号，并通过星载数据总线将信号数据输出至星上总控机端。星上总控机进行信号处理和角度解算，得到微角振动频率和幅值信息。

图1 MHD传感器测量原理图Fig.1 MHD sensor measurement schematic

为保证对卫星结构微角振动测量的高精度，本文采取的措施如下。

1.1 MHD传感器与有效载荷的同轴安装

MHD传感器星上安装位置示意图如图2所示。MHD传感器用于测量有效载荷的微角振动特性，因此将MHD传感器与有效载荷安装在同一个安装平台上，MHD传感器敏感轴垂面与安装平台贴合，与有效载荷振动轴的垂面平行。MHD传感器可以安装在有效载荷安装面的反面，以保证MHD传感器敏感轴与有效载荷振动轴的同轴度。

图2 MHD传感器安装位置示意Fig.2 MHD sensor installation location diagram

1.2 微角振动信号采用低电压差分信号(LVDS)方式传输

MHD传感器输出为模拟信号，需要将其转化为数字信号后用微控制器读取。

在空间环境中，用于信号传输的线缆会受到包括天体辐射的电磁波、高能粒子以及太阳发出的电磁辐射、宇宙线辐射等的干扰。干扰信号会与模拟信号与数字信号产生混叠，造成模拟信号失真和数字信号输出状态的改变。

由于数字信号相比于模拟信号抗干扰能力更强，同时差分传输相比于单端传输，具有对共模干扰的抑制效果，本文设计了一种采用差分方式进行数字输出信号线缆传输的方法，利用紧密靠近且等长的差分信号双绞线传输，将太空环境下传输线周围的各种电磁场辐射相互抵消，抑制其干扰[14]。各种逻辑电平标准中，选择LVDS作为数字输出的传输方式[15]。

由于微控制器不能直接读取LVDS电平，数字信号传输完成后，通过逻辑电平转换电路，可将信号转化为能被微控制器读取的晶体管-晶体管逻辑(TTL)电平形式。转换前信号与转换后信号需要进行噪声隔离。

1.3 小波降噪算法的信号处理方法

卫星结构微角振动信号一般为混频信号，测量过程中会引入MHD传感器噪声、AD输出噪声等噪声，导致信噪比最低时小于0 dB。为使测量精度更高，需要进行算法降噪处理。因小波降噪具有良好的时频特性和局部性质，适用于全频率、信噪比最低至负十几dB的信号[16]，适合应用于本系统，因此决定采用小波降噪算法进行信号处理[17]。

小波降噪基本流程如图3所示。首先使用合适的小波基对原始信号进行一层小波分解，然后对该层细节分量进行自相关系数R的分析。自相关函数为

(1)

式中：τ为延迟项；N为采样个数；Xi为采样的第i个数据；μ为均值；σ为标准差。如果自相关系数较小，说明该层细节分量主要为噪声，有必要进行下一层小波分解，直到某一层的自相关系数R≥0.6后，说明该层细节分量已经基本为有用数据。此时停止小波分解，并根据这一层及之前各层细节分量的自相关系数确定各层的去噪阈值λ。最后利用去噪阈值处理细节分量，并与分解最大层数的近似分量结合，重构信号，完成小波降噪。

图3 小波去噪流程图

(2)

自相关系数R=0时，λ与传统去噪阈值相同。R增大时，λ减小，在去除噪声的同时保留更多有用信号。

2 仿真及试验验证

2.1 信号处理仿真验证

对本文提出的信号处理方法进行仿真验证。在10 Hz、1个单位和50 Hz、1个单位的混频信号中加入2个单位的白噪声和0.8个单位的1/f噪声，选用小波降噪中的sym5小波基对加入噪声的信号进行降噪处理，得到理想信号、加噪声信号和信号处理后信号的波形如图4所示。

图4 理想信号、加噪声信号和处理后信号波形Fig.4 Ideal signal, noise added signal and processed signal waveform

计算加噪声信号和处理后信号的信噪比为

(3)

式中：Vs为信号幅值的有效值;Vn为噪声幅值的有效值。经信噪比计算，加噪声信号的信噪比为-0.168 5 dB，处理后信号的信噪比为9.372 1 dB。信噪比提升为

(4)

2.2 转台模拟试验验证

用某转台模拟有效载荷，转台可以提供0～100 Hz的单频正弦微角振动，频率精度为0.000 05‰，速率精度为0.05%，速率状态角度精度为0.05%，频率、速率和角度可以通过工控机端软件读取；将MHD传感器样机固定在转台转动轴心上，模拟MHD传感器与有效载荷的固连；用RS232总线模拟星载数据总线；用工控机模拟星上总控机，工控机同时可以控制转台转动以及读取转台理想微角振动信息。

以转台模拟10 Hz频率下较大速率(1°/s)和较小速率(0.1°/s)微角振动为例。控制转台进行上面两组微角振动，测量转台上MHD传感器样机的输出，得到原始信号。用1.3节所述小波降噪方法，选用sym5小波基对微角振动原始信号进行处理，得到小波降噪处理后信号。画出理想信号、原始信号和处理后信号的波形如图5所示。

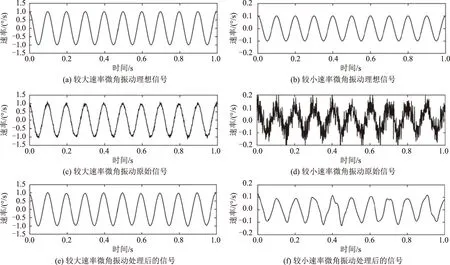
图5 理想信号、原始信号和处理后信号波形Fig.5 Ideal signal, original signal and processed signal waveform

经信噪比计算，较大速率微角振动信号经算法处理后信噪比提高了10.402 0 dB；较小速率微角振动信号经算法处理后信噪比提高了10.777 1 dB。

设初始微角振动角度为0；设t时刻微角振动角度为θ(t)，微角振动速率为ω(t)。物体在T时刻的角度为

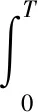
(5)

则微角振动理想角度信号和测量角度信号的波形图如图6所示。

经分析，较大速率微角振动的测量频率为10.01 Hz，测量幅值为0.016 1°；较小速率微角振动的测量频率为10.01 Hz，测量幅值为0.001 5°。

利用微角振动理想频率对本试验微角振动测量频率进行对比分析如表1与图7所示。

图6 理想角度信号和测量角度信号波形图Fig.6 Ideal angle signal and measured angle signal waveform

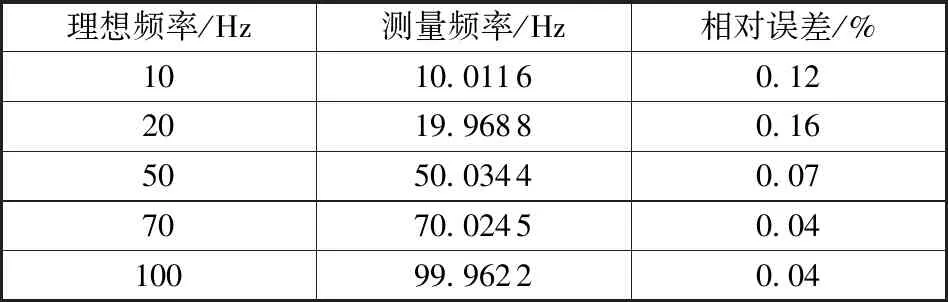
表1 微角振动理想频率与测量频率对比

图7 微角振动频率相对误差Fig.7 Relative error of micro-angular vibration frequency

利用微角振动理想幅值对微角振动测量幅值进行对比分析如表2与图8所示。

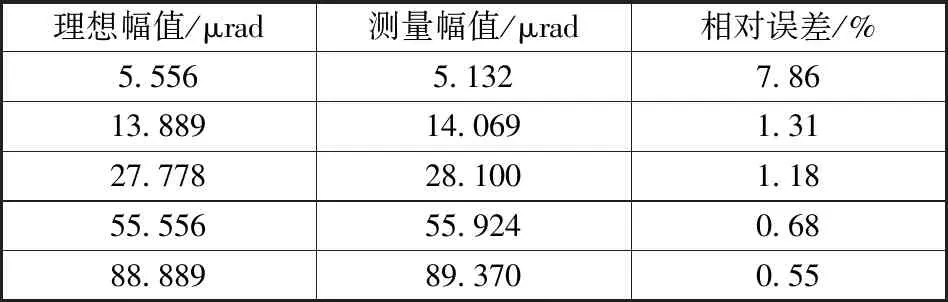
表2 微角振动理想幅值与测量幅值对比

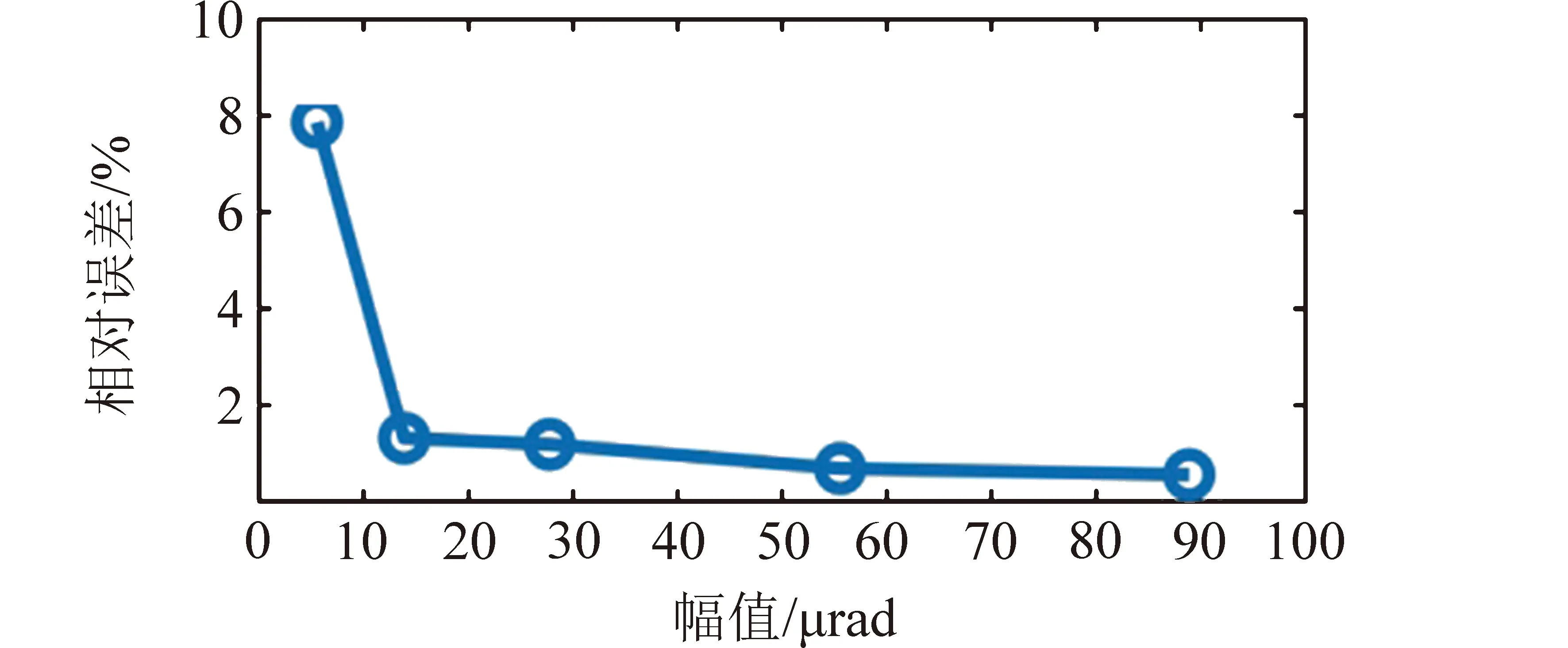
图8 微角振动幅值相对误差Fig.8 Relative error of micro-angular amplitude

2.3 结果分析

通过对图4理想信号、加噪声信号和处理后信号波形图的对比可以看出，本文所述小波降噪算法效果显著。信号处理前后信噪比的提升可以作为对降噪效果的证明。

通过对图5理想信号、原始信号和处理后信号波形图的对比可以看出，微角振动速率较大时，噪声对原始信号影响较小；微角振动速率较小时，噪声对原始信号影响明显增大。使用本文提出的小波降噪算法处理原始信号，可以有效降低噪声成分，提取有用信号。信号处理前后信噪比的提升可以作为对降噪效果的证明。

由表1看出，本试验微角振动测量频率与理想频率基本一致，相对误差小于0.2%；由表2看出，本实验微角振动测量幅值与理想幅值基本一致，相对误差小于8%。由此本文所述方法具有可行性。经国内相关文献的调研，现阶段微角振动测量频率精度可以达到0.1%，幅值精度可以达到15%。本文提出的方法频率精度水平与现阶段技术水平相当，幅值精度高于现阶段技术水平。测量幅值较小时，相对误差较大，幅值较大时，相对误差较小，这是因为MHD传感器存在本底噪声，当测量幅值较小时，本底噪声所占信号比例增大，造成相对误差的增大。因此，接下来的工作方向是降低MHD传感器的本底噪声以提高测量精度。

3 结束语

本文根据卫星结构微角振动特点和卫星在轨微角振动测量要求出发，利用MHD传感器带宽宽、精度高、尺寸小的特点，提出了基于MHD传感器的卫星微角振动高精度测量方法。经仿真及转台模拟试验验证，本方法频率精度优于0.2%，幅值精度优于8%，具有对有效载荷微角振动精确测量的可行性。本方法可在卫星姿态控制和卫星有效载荷微角振动补偿等领域得到应用。