涡轮增压器涡轮叶轮有意失谐强迫振动特性研究

王智慧,马朝臣,黄智

(1.北京理工大学机械与车辆学院, 北京 100081；2.晋中学院机械学院，山西 晋中 030619)

在设计增压器叶轮的过程中，涡轮叶片通常设计成协调的，这样叶盘结构扇区具有完全相同的物理参数和结构参数，也就是所谓的圆周循环对称结构。然而由于加工误差和工作磨损等原因，叶片之间的属性存在小的随机偏差，称为失谐。失谐可能会对叶轮的动力学行为产生严重的影响，特别是会引起振动能的空间局部化，某些叶片将会承受更大的交变应力。研究表明[1-5]，叶轮的失谐和强迫振动的统计学特性非常重要，因为叶轮叶片的属性存在微小变化是随机的，很难人为控制和精确测量。因此对失谐系统的统计学强迫振动特性进行研究具有现实的意义。

统计学方法通常可以使用有限的数据来预测一组产品的耐用性，一般使用Monte Carlo仿真判断叶轮强迫振动幅值超过某个危险值的可能性。为了取得精确的预测结果，要对叶轮的有限元模型进行多次仿真，计算量很大，因此需要使用基于循环对称结构的缩减模型来减少计算时间。本研究使用基于模态综合法的子结构模态失谐方法 (CMM法)计算叶轮的失谐强迫振动，该方法最早由Lim[6]提出，可系统处理不同形式的叶片失谐。

关于叶轮机械的失谐特性国内已有一些学者进行了研究。张长海[7]对失谐叶轮的动力性进行了深入研究，数值模拟了失谐因素对叶轮固有频率和模态的影响，并研究了频率转向特征与失谐敏感性的关系，提出了确定叶轮失谐敏感性的有效方法。贺源[8]围绕失谐叶片， 对叶片振动的测量方法进行研究，采用共振法和叶尖定时法对失谐叶片振动进行了非接触测量，同时验证了仿真结果的准确可靠性。尚海等[9]通过主成分分析方法，研究失谐叶片和机床误差的关联，分析失谐的来源，并提出了有效提高加工精度的方法。刘战合等[10]基于气动力降阶模型提出了一种高效的叶轮机失谐叶片流固耦合分析方法，通过改变部分叶片的结构参数研究了失谐对系统流固耦合颤振稳定性的影响，结果表明，刚度失谐可以明显改善系统的颤振稳定性，但也会导致模态局部化，失谐方式、失谐量和流固耦合作用对失谐系统的颤振稳定性都有明显影响。

有意失谐是指在叶轮系统中人为地对某些叶片加入一定的属性偏移量，以达到减小强迫振动程度的目的。即使是对较小程度的失谐来说，不同的有意失谐形式也会对叶轮的强迫振动产生影响。关于有意失谐近些年国内外也进行了一些研究。Kaza[11]等研究了失谐频率对风扇叶片颤振的影响，使用一个气动模型计算了气动载荷，显示交替的有意失谐形式可以有效增加叶排的稳定性。Nowinsky[12]等通过试验验证了交替的有意失谐会对叶片的振动控制产生有利影响。J Kenyon[13]等设计并测试了一个简单的叶盘，通过增加叶尖质量的有意失谐计算方式达到振幅的最大响应。Yanrong Wang[14]等研究了有意失谐对压气机转子叶片气弹稳定性的影响，分析了4种有意失谐形式对随机失谐的敏感性。使用有意失谐方案后，实际中的强迫振动仍然会很大程度地受到额外随机失谐的影响，因此采用有意失谐必须解决的核心问题是如何在设计中减低叶轮对随机失谐的敏感性。而关于如何降低叶轮对有意失谐过程中随机失谐敏感性的研究甚少，本研究对给定的涡轮增压器涡轮叶轮使用有意失谐方案以减少其强迫振动幅度以及随机失谐敏感性，这对改进现有的叶轮设计方案，减轻高周疲劳问题至关重要。

1 失谐叶轮动力学特性

1.1 叶轮失谐模型

本研究中模型为具有12个叶片的增压器涡轮，使用CMM方法计算失谐强迫振动。缩减模型取叶轮的1/12作为基扇区进行建模(见图1)，分为叶片和叶盘两个子结构。叶片部分使用六面体网格划分，底盘部分使用四面体网格划分，使用固定界面法处理子结构之间的交界面。基扇区总网格节点数15 076个，单元数7 246个。涡轮叶轮所用材料为镍铬铁合金，密度为7 860 kg/m3，泊松比为0.3，杨氏模量为1.1×105MPa，屈服强度为726 MPa。在涡轮的轴心位置施加固定约束。

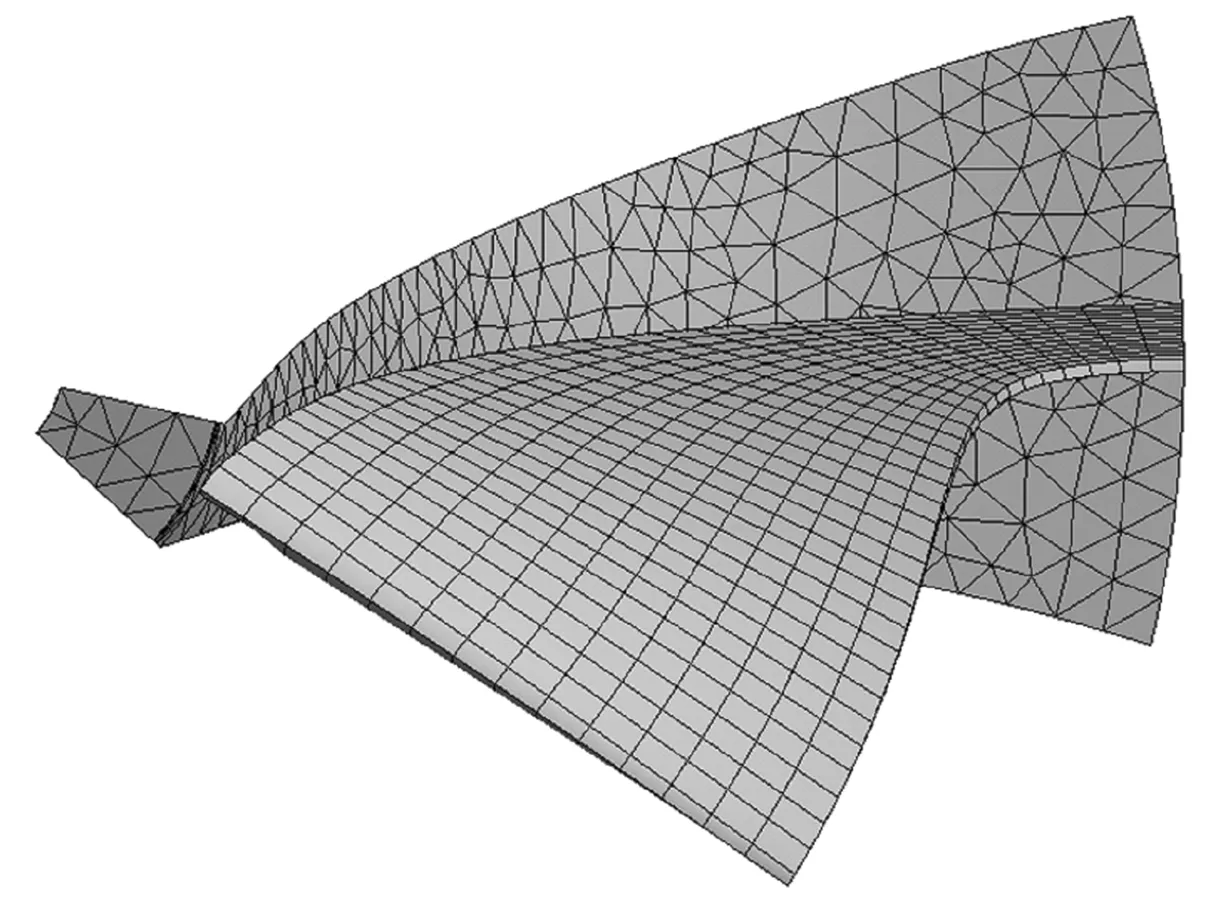
图1 叶轮有限元模型

叶盘结构制造加工或安装、材料的分散性以及工作磨损等原因往往会引起叶片几何参数上的差异，而结构几何失谐又会导致各个叶片的刚度和质量发生变化，传统的处理方法是修改弹性模量参数作为失谐变量，为简化起见，本研究使用改变杨氏模量的方式表示叶片的微小失谐[19]，即刚度失谐。对于初始的叶轮基准设计，所有叶片都是相同的，每个叶片的名义刚度为

kn=k0,n=1,...N。

(1)

实际上任何叶轮叶片都不可避免地存在一些随机失谐，对于叶轮上的第i个叶片，其叶片刚度为

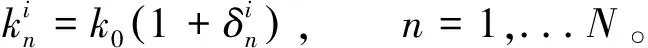
(2)

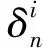
1.2 加速Monte Carlo方法

为了估计叶轮失谐强迫振动的统计学特性，本研究采用Monte Carlo方法进行仿真分析，基本步骤如下：

1) 对随机失谐给定一个标准差，使用随机数生成器生成一组刚度值，将其赋予第i个叶轮的叶片。该叶轮共有12个叶片，每个失谐叶轮样本需要12个随机数，随机数服从均匀分布。

2) 进行扫频仿真计算，找到叶轮叶片的最大响应值。

3) 将失谐叶片的最大响应幅值除以谐调叶轮的最大响应值，得到第i个叶轮的幅值放大系数。

重复以上过程，对多个随机失谐的叶轮进行谐响应分析，数据处理后可以得到叶轮失谐的统计学特性。即使使用了缩减模型，若要计算1 000个失谐叶轮，计算量仍然很大。因此要对Monte Carlo方法进行加速，减少计算的样本数。根据极值统计理论，叶片强迫振动的最大幅值分布趋近于三种极值分布之一[15]。由于振动响应值是有界的，叶片的响应分布将渐近于第三极值分布，即Weibull分布。Mignolet等[16]的研究结果也证实了这一结论。

三参数Weibull分布的分布函数如下式：

F(x)=e-((λ-x)/δ)β。

(3)

对应的概率密度函数为

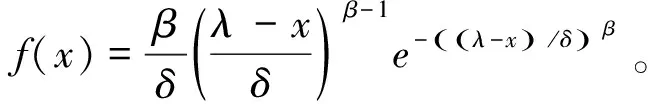
(4)

式中：δ，β和λ分别为缩放、形状和位置参数；x为需要研究的随机变量，这里为失谐叶轮叶片的最大响应值。

1.3 失谐叶轮模态与响应特性

谐调叶轮模态振动特性可以使用固有频率和节径数的关系图表示(见图2)。图2中给出了前4阶模态的频率，并将同一模态族的模态连成线。图中叶片显著模态的频率基本相同，连线近似于水平线。而二阶、三阶和四阶模态族的1节径模态相比0节径模态频率有升高的现象，这是因为底盘的模态刚度随着节径增加而升高，这些模态属于底盘显著模态。叶片显著模态的叶盘振动较小，因此叶片间的耦合作用也相对较弱，而底盘显著模态的叶片间耦合作用则较强。叶间耦合在叶轮振动中起到很重要的作用，它决定着振动能量在叶片之间传递程度。因此底盘显著模态(通常位于频率线的斜线部位)在失谐的时候有可能会引起更大的振动幅值。

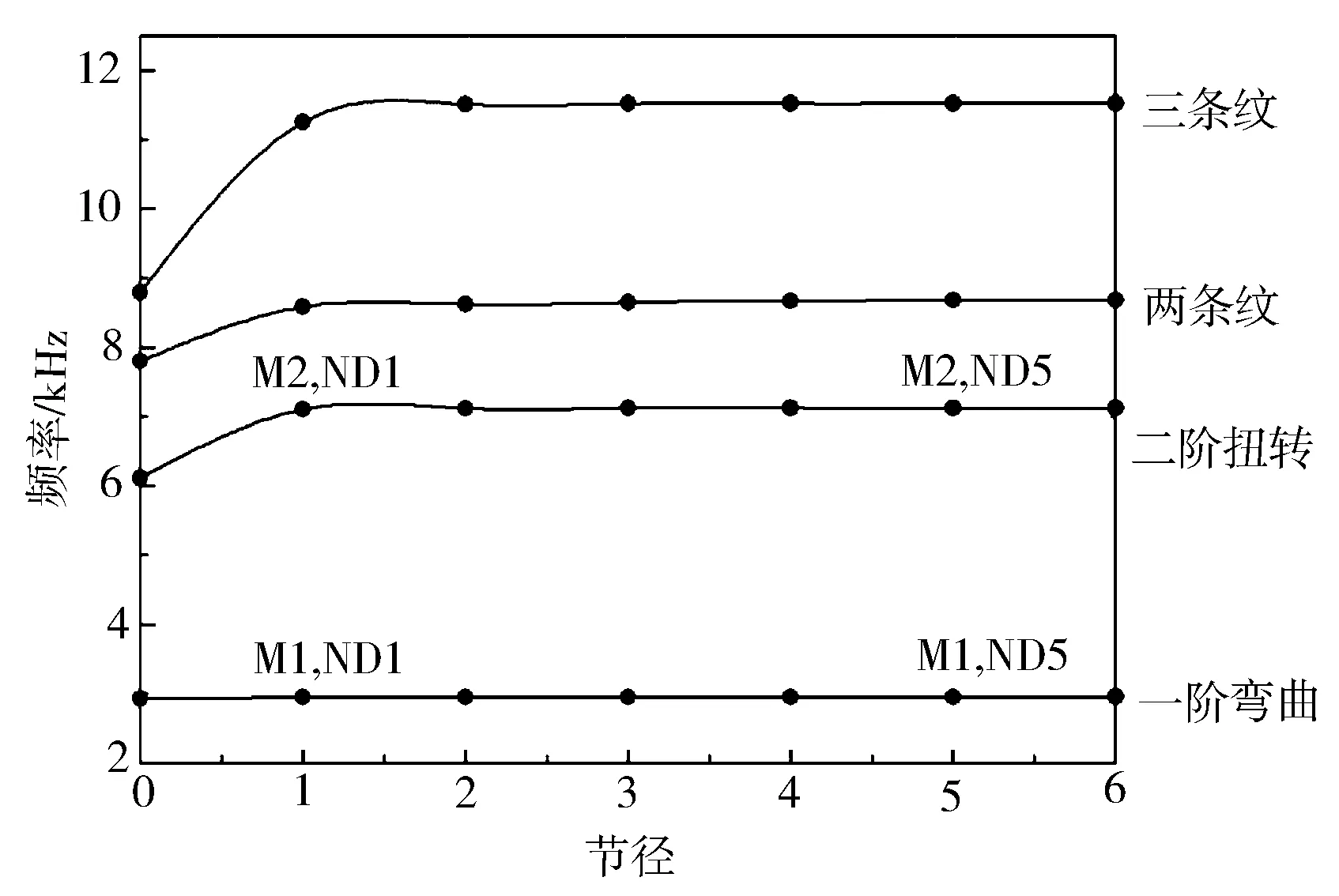
图2 节径与模态频率关系图

为了观察失谐叶轮的强迫振动特性，从方差σ=0.05 的随机失谐叶轮中取出一个样本，对其施加EO1(即引擎阶次为1)的气动激励，进行谐波响应扫频分析。图3a示出原始未失谐叶轮在激振频率达到2 750 Hz时(即叶轮的一阶模态族频率)的强迫振动振型，图3b示出失谐叶轮在同样的激振力达到2 750 Hz时的强迫振动振型。可以看到谐调叶轮的响应表现为节径数为1的形式，与激振力的节径数相匹配。在失谐叶轮的谐振中依然可以观察到节径线的存在，然而可以看到其节径线两侧叶片的增幅不再是完全对称的形式。节径线左侧的叶片振幅明显要大于右边的叶片。这是由于失谐导致叶轮的振动能在某些叶片上更为集中，因此在这些叶片上的振幅和交变应力都更大。图4示出失谐叶轮的12个叶片在1 500～3 500 Hz频率段内的响应情况，可以看到失谐造成各个叶片达到最大响应的频率不再相同，最大响应幅值也各不相同，而谐调叶轮各个叶片的最大响应频率都应为2 750 Hz。

图3 失谐叶轮与谐调叶轮强迫振动

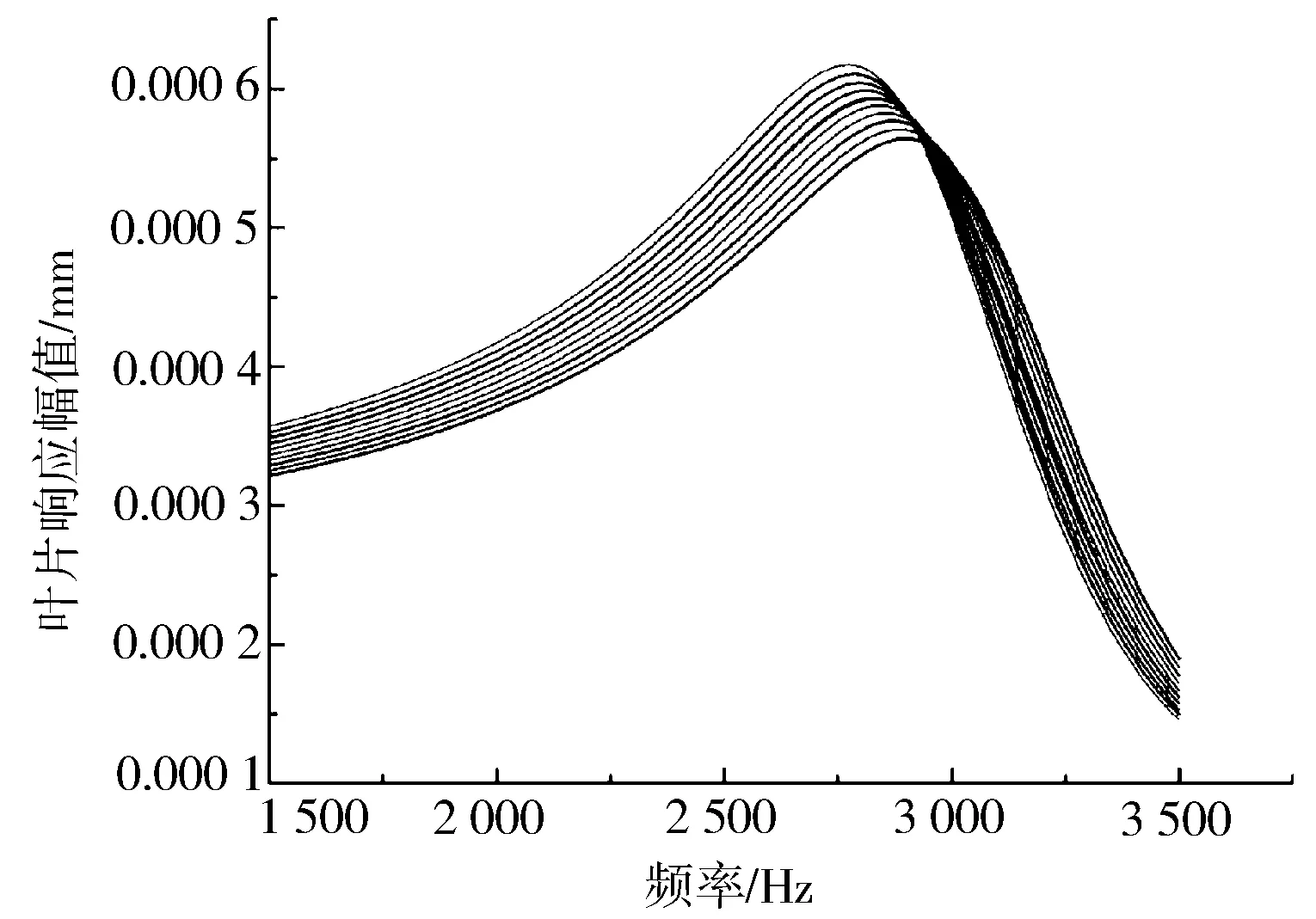
图4 失谐叶轮各叶片振幅

为了研究叶轮对失谐的敏感性，对每个失谐标准差生成300个随机样本进行扫频仿真，计算结果使用Weibull分布估算最大谐振幅值。图5示出了失谐标准差为0.05时，叶轮叶片在频率为2 750 Hz的EO1气动激励作用下的最大振动幅值的统计结果，失谐振动的幅值放大系数分布范围为1.2～1.65。将该分布范围分为16个分组，用直方图可以体现幅值放大系数处于各个分组区间内的失谐叶轮的出现概率，图5中的曲线为用于拟合直方图的Weibull概率密度函数。将密度函数积分可得到分布函数，如图6所示。从分布函数曲线可以反求出各个百分位的幅值放大系数，例如95百分位对应的幅值放大系数为1.52，其含义为只有5%的失谐叶轮叶片的幅值放大系数超过1.52。

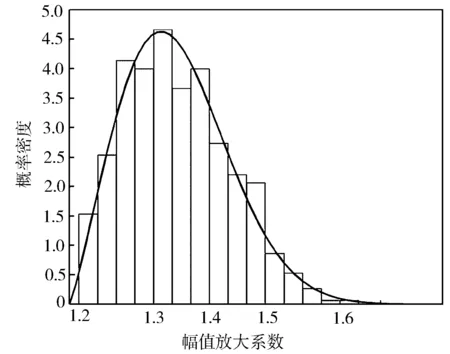
图5 谐振幅值分布与Weibull概率密度函数拟合

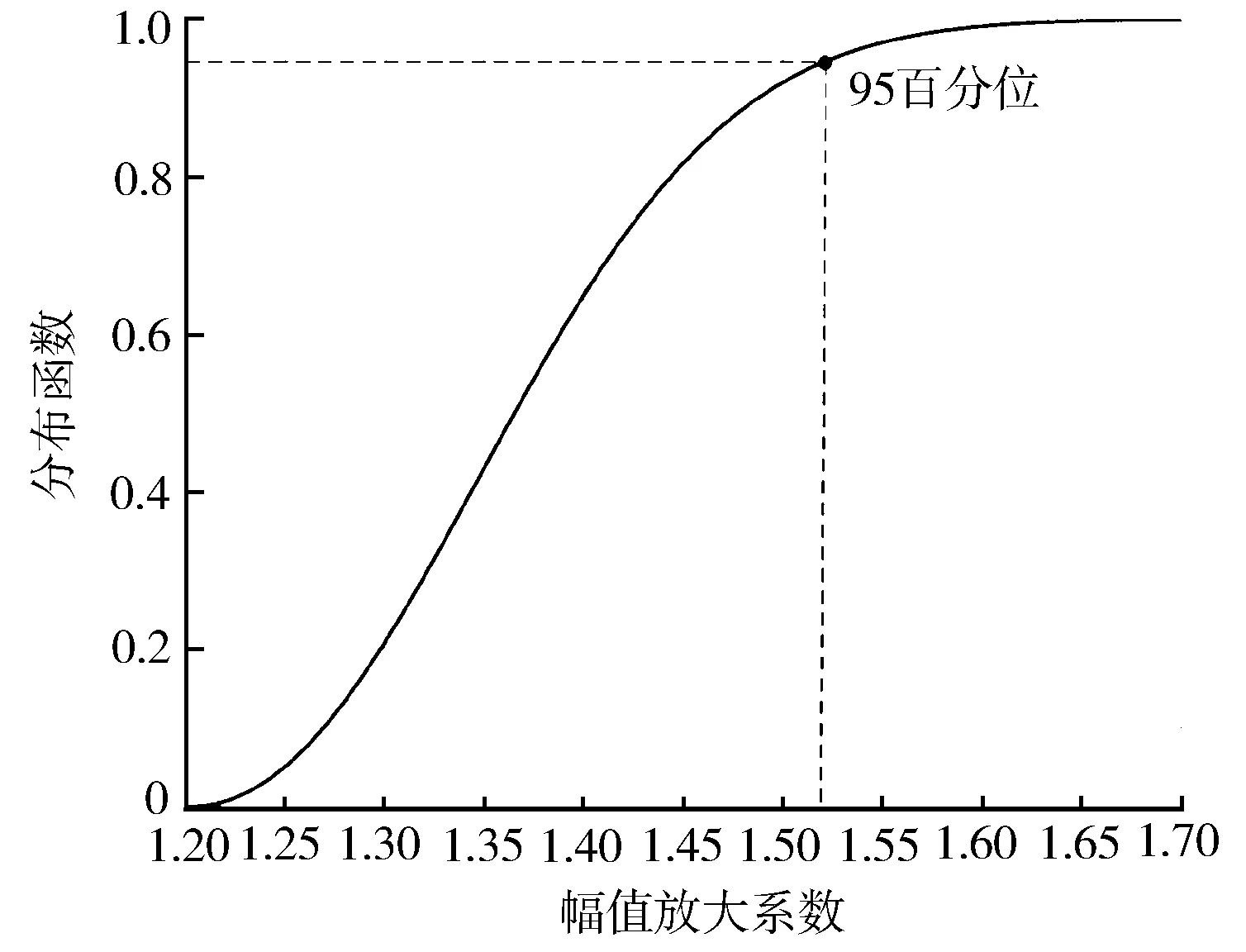
图6 Weibull分布函数

使用上述的Weibull分布计算叶轮响应幅值放大系数的方法，对不同失谐标准差的叶轮作Monte Carlo统计分析，可以研究叶轮对失谐的敏感性。图7示出谐调叶轮在失谐时，分别使用EO1气动激励和EO5气动激励作用在叶轮上，在一阶模态族对应频率时叶轮的99百分位幅值放大系数与失谐标准差的变化关系。由于这两种气动激励刚好与节径1的一阶模态(M1,ND1)和节径5的一阶模态(M1,ND5)相匹配，所以这两个模态分别会被EO1和EO5激励最大程度激起。可以看到在失谐标准差为0.01附近时幅值放大系数达到最大值，这种局部出现峰值的现象与Ottarsson和Pierre等[17-18]的观察一致，因为失谐会影响叶片之间的耦合程度，如果叶间耦合程度很弱，每个叶片相当于各自单独振动，则失谐叶轮的响应与谐调叶轮的响应相比不会相差太大。当耦合程度增加时，叶盘之间的振动能量可以相互传递，增加了振动能聚集在某几个叶片上的可能性，导致了响应峰值的出现。继续增加失谐量，叶片之间的强耦合作用使得各个叶片的振动能可以在叶片之间迅速交换，振动能难以再聚集在叶轮的局部，叶轮的响应相对减小。

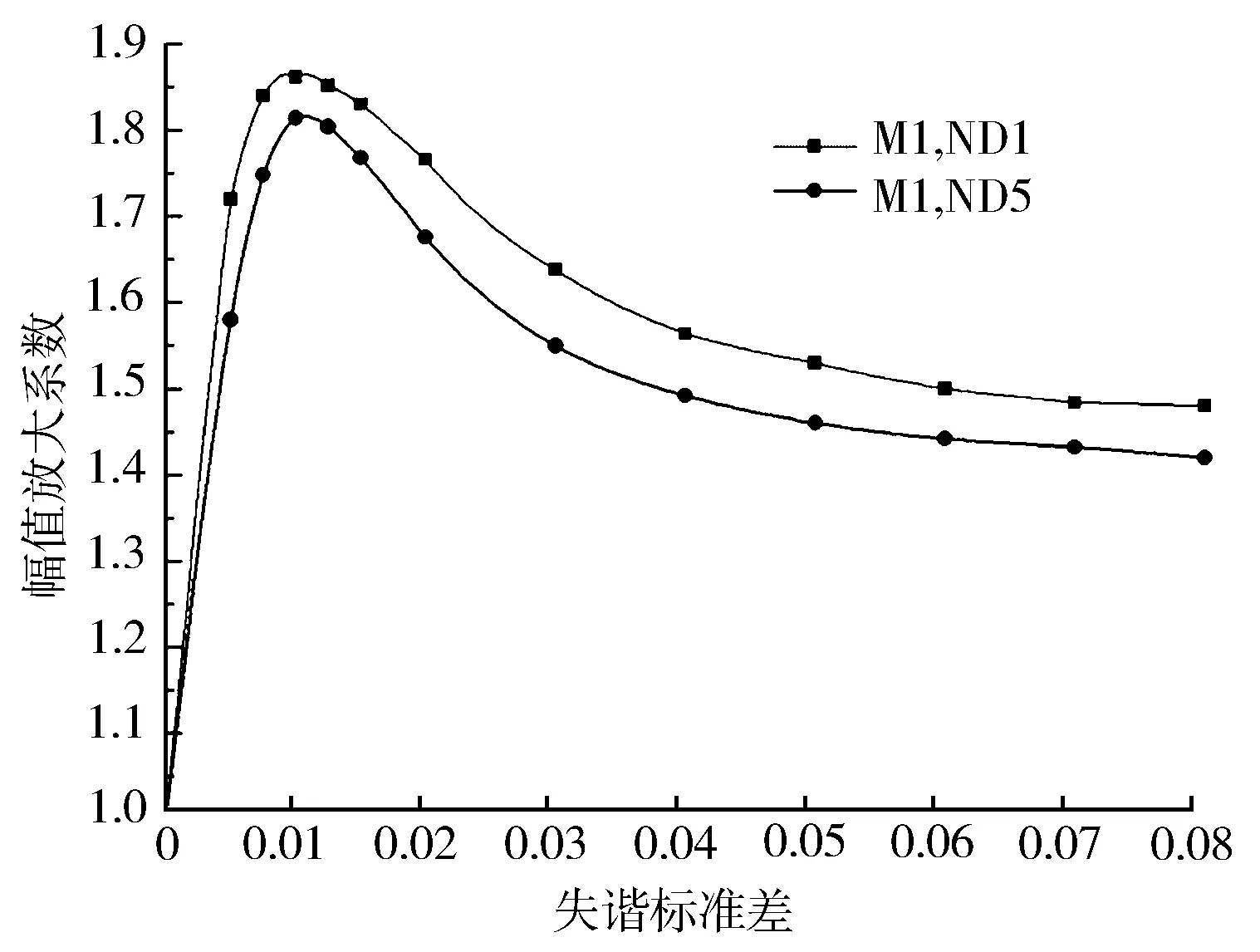
图7 (M1,ND1)和(M1,ND5)处的失谐响应敏感性

图8示出谐调叶轮在失谐时，分别使用EO1气动激励和EO5气动激励作用在叶轮上，在二阶模态族对应频率时叶轮的99百分位幅值放大系数与失谐标准差的变化关系。可以看到随着失谐标准差的变化，叶轮的响应幅值放大系数同样出现了峰值。不同于上面的一阶模态族失谐响应的是，在EO5激励下的叶轮响应幅值比EO1激励下的响应幅值有较大程度降低。这是由于EO1激励主要激起节径1的二阶模态(M2,ND1)，该模态位于频率转向区域，属于底盘显著模态，具有较大的叶间耦合程度，故其失谐响应幅值也较大。

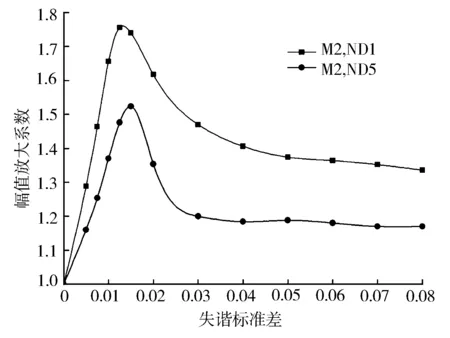
图8 (M2,ND1)和(M2,ND5)处的失谐响应敏感性

2 叶轮有意失谐强迫振动分析

2.1 有意失谐方案

从上面的分析可以发现，谐调叶轮对失谐的敏感性很高，在较小的失谐标准差下即可达到幅值放大系数的峰值。鉴于完全的循环对称结构对微小失谐的敏感性过高，因此有意地将叶轮做成非谐调的，可能有助于减轻叶轮对随机失谐的敏感性。在设计的时候加入足够的失谐量，使得在设计点的叶轮在出现微小失谐时，其失谐量已经超过了响应峰值点，从而降低叶轮的失谐敏感性。

现在将有意失谐引入到叶轮的设计中来。对于原始的谐调叶轮设计，每个叶片的刚度都为k0。对于有意失谐设计，每个叶片的刚度为

kn=k0(1+Δn),n=1,...N。

(5)

由于叶轮具有循环对称性，在选择有意失谐方案时可以利用这一特点，将失谐叶片按一定的周期性进行布置，这样也可以满足动平衡的要求。考虑到加工成本的问题，有意失谐方案中的叶轮仅使用两种类型的叶片(分别用a和b表示)。对于12叶片的叶轮，两种类型叶片的失谐形式有3种，如图9所示，a叶片刚度与原始谐调叶片相同，增加b叶片的刚度，Ⅰ型为两种叶片间隔布置，Ⅱ型为两种叶片两两间隔布置，Ⅲ型为两种叶片三片间隔布置，以达到循环对称效果，以引入有意失谐。叶轮的失谐标准差取为0.05。

图9 有意失谐形式

即使对叶轮使用了有意失谐设计，依然会存在制造误差和工作磨损的问题，因此叶轮叶片与设计值相比仍然会有随机偏差，即随机失谐仍然存在。对于随机失谐的第i个叶轮，叶片刚度可使用下式表示：

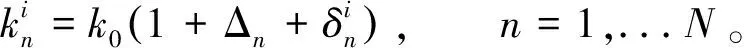
(6)

2.2 有意失谐强迫振动特性

图10至图12示出了3种有意失谐设计的叶轮在EO1气动激励下的失谐敏感性曲线，激励频率为一阶模态频率，幅值放大系数取为99百分位的值。由图10可以看到方案Ⅰ的叶轮强迫振动敏感性曲线仍然具有峰值的特征，峰值对应的失谐标准差值比谐调叶轮的略有降低，因此该方案叶轮仍旧对失谐敏感，然而其振动响应幅值得到了一定程度的降低，由谐调叶轮的1.86降到了1.68。图11示出方案Ⅱ叶轮强迫振动敏感性曲线，可以看到响应峰值已经不再明显，最大响应值降到了1.58。图12示出方案Ⅲ叶轮强迫振动敏感性曲线，可见曲线上升比较平缓，最大响应值为1.49，在微小失谐时响应值较低，表明该有意失谐方案叶轮对失谐不再敏感。因此在设计中采用方案Ⅲ可有效地降低失谐对叶轮强迫振动的影响，提高叶轮的可靠性。

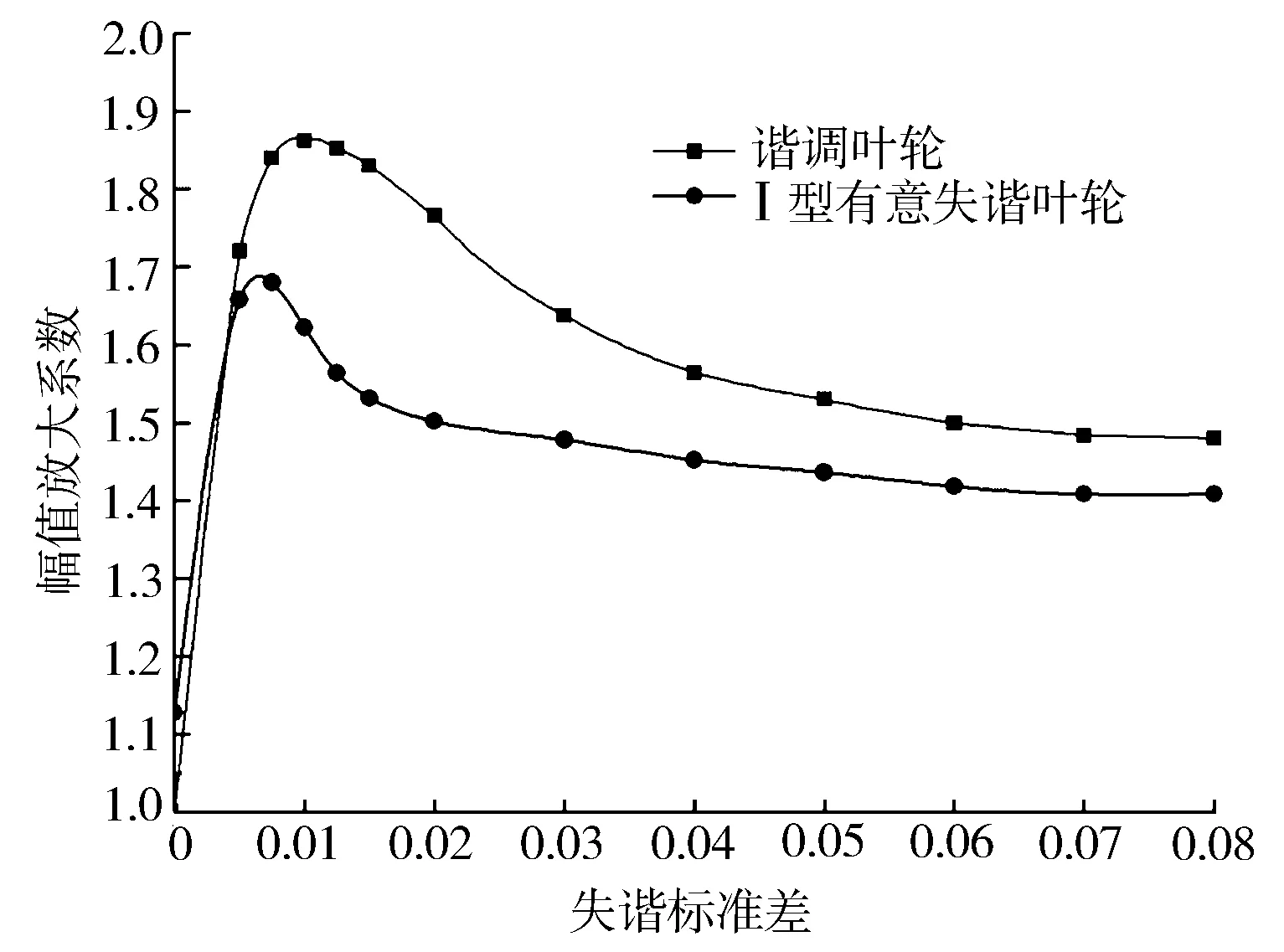
图10 方案Ⅰ失谐响应敏感性

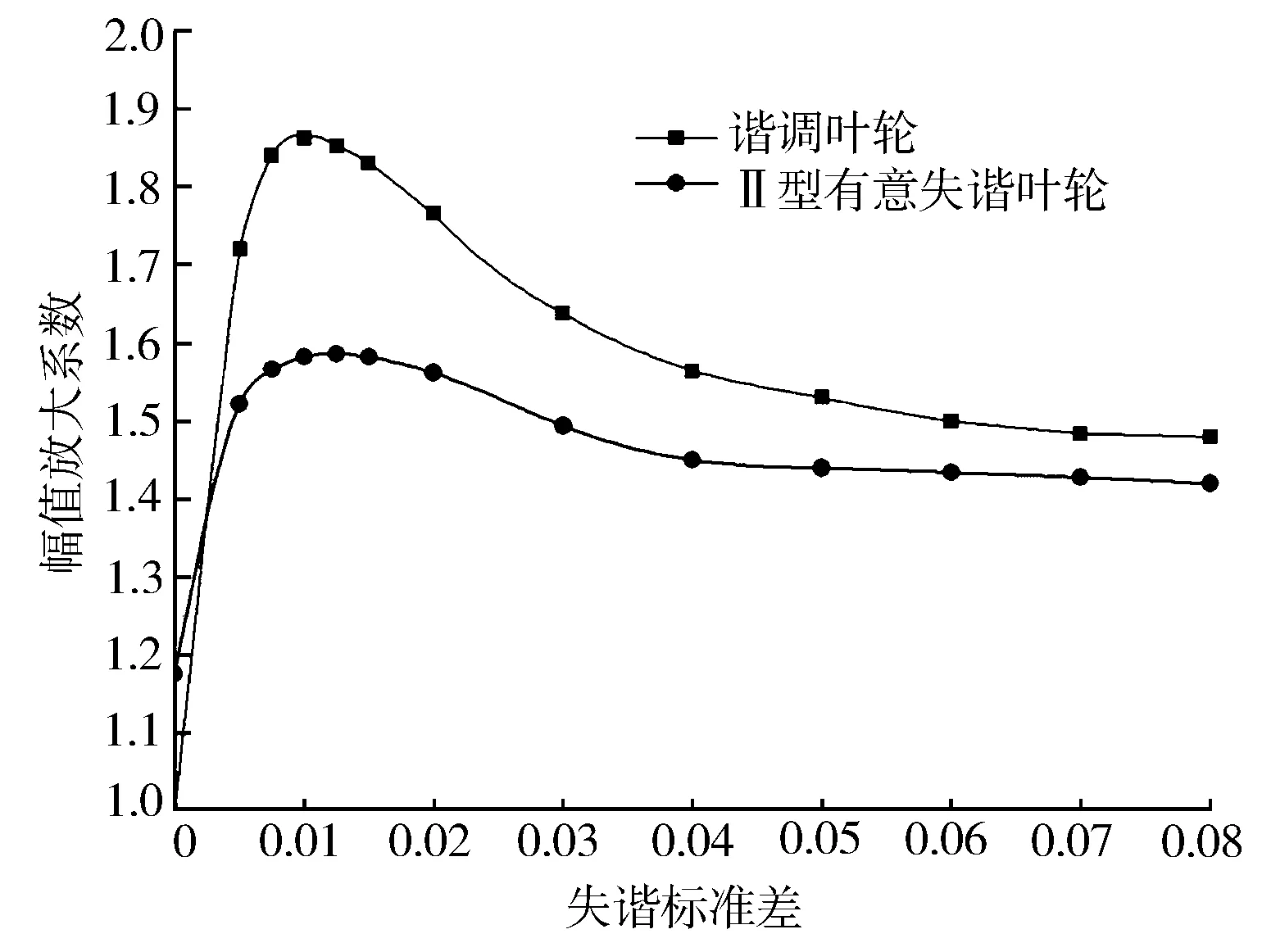
图11 方案Ⅱ失谐响应敏感性

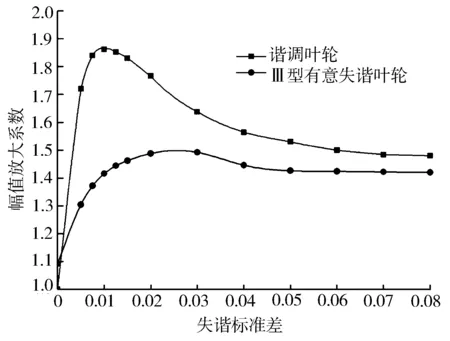
图12 方案Ⅲ失谐响应敏感性

可以看到方案Ⅲ对失谐的敏感性最低，以下探寻有意失谐在叶轮随机失谐响应中起到的作用。图13和图14分别示出了谐调叶轮和方案Ⅲ叶轮出现失谐并受到EO1激励作用时的模态系数分布情况(激励频率为一阶模态频率)。可以看到谐调叶轮和方案Ⅲ叶轮在失谐时所有节径数(ND0，ND1，…ND6)的模态都对激励产生响应，这是因为失谐破坏了叶轮的循环对称性，响应中包含了更多节径的模态。

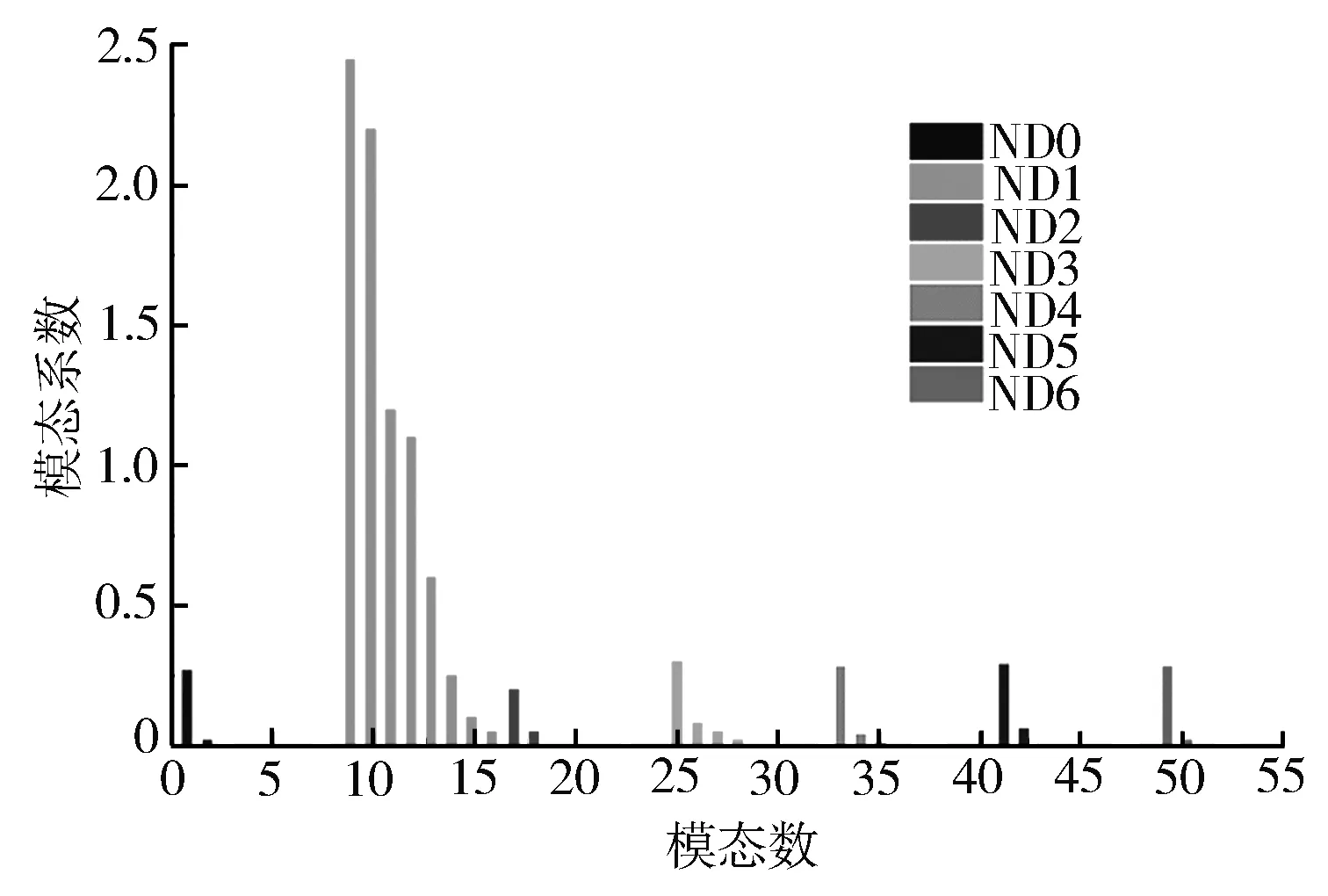
图13 谐调叶轮谐响应模态系数

图14 方案Ⅲ叶轮谐响应模态系数

由于激励和模态节径数匹配的关系，两种叶轮在EO1激励作用下激起的都主要是节径1的模态。可以观察到谐调叶轮的节径1模态响应更大，最大模态系数达到了2.45，而方案Ⅲ叶轮的最大模态系数为1.67。由于激励频率对应的刚好为一阶模态族，所以各节径的模态中主要激起的都是低阶模态。然而，谐调叶轮失谐响应时ND1之外的其他节径的模态响应较弱，每种节径数的模态大多仅有前2阶模态被激起。而方案Ⅲ的叶轮除了节径1模态之外，其他节径的模态被激起的程度则相对较大，前4阶模态都对激励有响应。因此，谐调叶轮随机失谐时强迫振动中的模态响应主要集中在匹配节径的模态上。而采用了有意失谐方案Ⅲ之后，强迫振动的模态响应成分更多地转移到其他节径的模态上，从而在受特定的EO1激励时，节径1的模态不会被大幅度地激起，减轻了叶轮强迫振动的程度。由于有意失谐方案的叶轮响应中各个节径模态的贡献更为平均，因此更不容易受到随机失谐的影响，降低了对失谐响应的敏感性。

3 结论

a) 对谐调叶轮进行模态分析发现，二阶、三阶和四阶模态族的1节径模态相比0节径模态频率有升高的现象，属于底盘显著模态；使用EO1气动激励和EO5气动激励作用在叶轮上，在一阶模态族对应频率时主要激起的模态分别为M1，ND1与M1，ND5；研究发现这两种激励情况下，失谐标准差为0.01附近时幅值放大系数存在峰值；失谐会影响叶片之间的耦合程度，当耦合程度增加时，增加了振动能聚集在某几个叶片上的可能性，导致响应峰值出现；

b) 使用EO1气动激励和EO5气动激励作用在叶轮上，在二阶模态族对应频率时主要激起的模态分别为M2,ND1和M2,ND5；随着失谐标准差的变化，叶轮的响应幅值放大系数同样出现了峰值的现象，不同于一阶模态族失谐响应的是，在EO5激励下的叶轮响应幅值比EO1激励下的响应幅值有较大程度降低；由于M2,ND1属于底盘显著模态，具有较大的叶间耦合程度，其失谐响应幅值也较大；

c) 失谐方案Ⅰ的叶轮强迫振动敏感性曲线仍然具有峰值的特征，但振动响应幅值得到了一定程度的降低；方案Ⅱ的叶轮强迫振动敏感性曲线响应峰值已经不再明显，最大响应值相比谐调叶轮的幅值放大系数由1.86降到了1.58；方案Ⅲ的叶轮强迫振动敏感性曲线上升比较平缓，最大响应幅值放大系数为1.49，微小失谐时响应值较低，方案Ⅲ叶轮对失谐不再敏感。