考虑线性佣金率和保留价的拍卖模型

●杨卫星

经典的拍卖理论研究中，保留价受到了足够的重视①②③。代表性的结论如下：Samulson①给出了一级价格密封拍卖中卖者的最优保留价满足的必要条件。McAfee②用更简便的方法得到了与Samulson①相同的结论，而且给出了最优保留价应该满足的充分条件。

相比保留价的研究，拍卖佣金的研究成果并不多。与文章密切相关的文献评述如下：王彦④把佣金率引入传统的一级和二级密封式拍卖中，研究了佣金率对拍卖结果的影响,但他们只考虑了常数佣金率的情况。Wang⑤引进了线性佣金率，并与文献④中佣金率为固定比例的情况做了对比。美中不足的是，文献⑤中只对均匀分布的特殊情形做了证明。杨卫星等⑥在文献⑤的基础上继续研究带有线性佣金率的拍卖模型，给出并证明了一般分布下的一级和二级密封式拍卖的投标策略，弥补了文献⑤的不足。

以上的文献④⑤⑥虽然充分重视了佣金的作用，但是又忽略了保留价的影响。刘树林等⑦进一步将佣金率内生化，研究了一类同时带有保留价和佣金率的密封式拍卖模型，首次考虑了拍卖行的最优佣金率问题，并且给出了最优佣金率满足的必要条件和充分条件。冉茂盛等⑧建立了带有佣金率以及保留价的一口价拍卖模型，研究了卖者的最优一口价和最优保留价，并且讨论了拍卖行的最优佣金率问题。

通过以上的文献综述发现，一个好的拍卖模型应该同时考虑佣金率和保留价这两个因素，才能更加贴合实际。文章在前人的研究基础上，假设收取的佣金与成交价成线性关系，研究同时带有线性佣金率和保留价的密封拍卖模型。在估值服从一般分布时，得到了投标人的均衡投标策略，并求出投标人、卖者以及拍卖行的预期收益。进一步分析线性佣金率的两个系数对拍卖参与各方的影响。

一、模型及假设

假设投标者i 对卖品的估价为νi，νi独立同分布，分布函数为F（ν）,ν∈[ν,]。

本模型中，拍卖行设定线性佣金率k=k0- k1b，其中k1＞0，b≥0，b 为报价，0≤k≤k0，k0表示法规允许的最大佣金率。卖方设定保留价r,保留价的设定使得拍品的成交价不低于r，因此，对于参与和不参与拍卖无差别的最低估价v·满足π（ν*，b（ν*））=0（其中π（ν，b） 表示受益函数），即：ν*- b（ν*）（1+k0- k1b（ν*））=0，可以得到ν*=r（1+k0- k1r）。

二、投标人的投标策略

（一）一级价格密闭式拍卖

定理1：在同时带有线性佣金率k=k0- k1b 和保留价r 的拍卖模型中(以下简称本模型),若采用一级价格密封式拍卖的方式,均衡报价策略为：

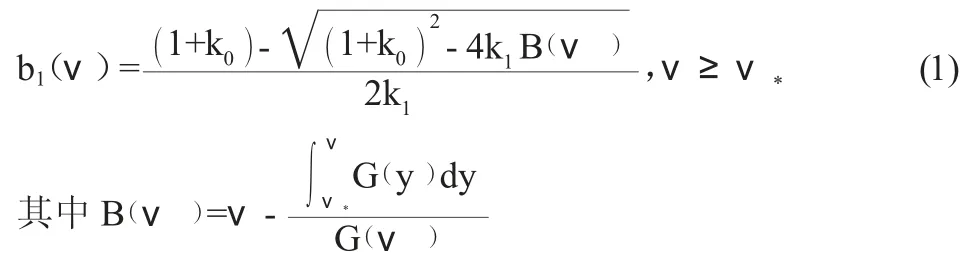
证明：假设投标人有递增的均衡投标函数b1（ν），当某投标人的私人估价为ν 而报价为A 时，他的预期收益是：

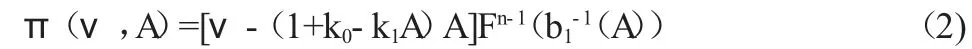
在贝叶斯- 纳什均衡中，当A=b1（ν）时投标者获得最大的预期收益，因此有由包络定理可以得到：

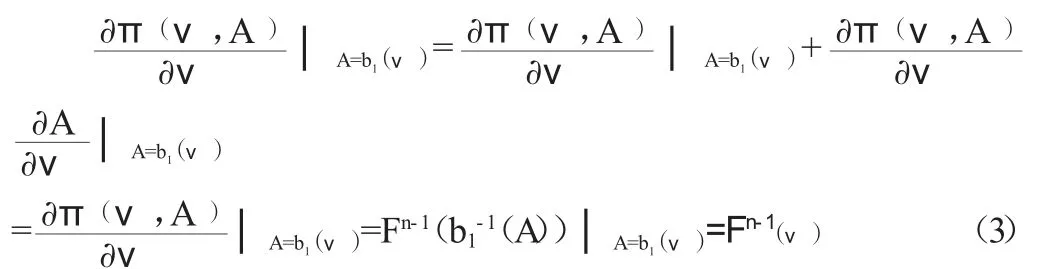
把微分方程(3)两边同时求积分得：

又因为π（ν，，b1（ν，））=0，以及

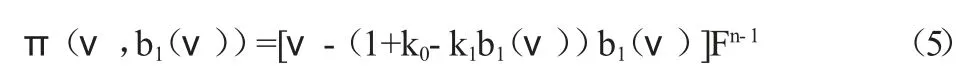
令B=（ν）=（1+k0-k1b1（ν））b1（ν），由上面两式(4)和(5)可解出：

其中B（ν）和Samulson[1]的结论一致，即和只考虑保留价，不考虑佣金时的投标策略一致。进而有（1+k0）b1（ν）-k1b12（ν）=B以及

当△=（1+k0）2-4k1B（ν）≥0 时，即（1+k0）2≥4k1B（ν）时，方程（7）的解为

得到下面的推论1 。

推论1：在本模型中，截距项k0越小，投标人报价越高；斜率项k1越小，投标人报价越低；保留价r 与报价呈正相关关系。

（二）二级价格密闭式拍卖

定理2：在本模型中，若采用二级价格密封式拍卖，均衡报价策略为：

证明：类似王彦等人④的证明。

三、收益比较

（一）卖方的收益比较

定理3：收益等价定理在本模型中不成立，如果投标人数比较多，应该选择第二价格拍卖。

证明：卖者在一价拍卖中的预期收益为：

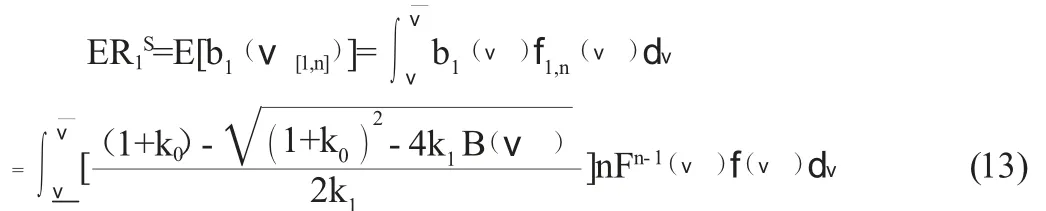
其中ν[1，n]表示ν1，ν2，……νn中的最高次序统计量，f1,n（ν）为ν[1，n]的密度函数。

卖者在二价拍卖中的预期收益为：

其中ν[2,n]为ν1,ν2,…νn中的次高次序统计量，f2，n（ν）为ν[2,n]的密度函数。

下面做比较静态分析，前面的讨论已经得出：得到下面的推论2。

推论2：在一价和二价拍卖模型中，卖方的预期收益和保留价r 正相关，和k0负相关，但和k1正相关。

（二）拍卖行的收益比较

定理4：本模型与不考虑佣金时的情形相比较，卖方的预期收益减少，减少的部分是拍卖行的预期收益。

证明：在一价拍卖中，拍卖行的预期收益为：

同理，在二级价格密封式拍卖中，拍卖行的预期收益为：

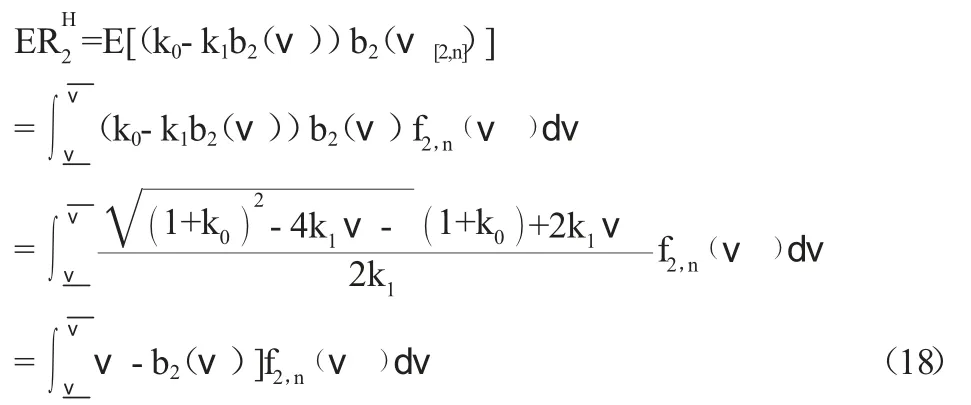
下面做比较静态分析，同样因为

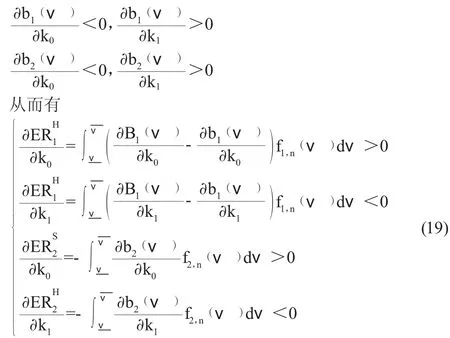
得到下面的推论3。

推论3：在一级和二级价格密封式拍卖中，拍卖行的预期收益和k0正相关，但和k1负相关。

（三）投标人的收益比较

定理5：在本模型中，就一级和二级密封式拍卖两种方式相比较，投标人在一级拍卖中获得更多的预期收益；二者均和k0成反比，和k1成正比，和r 也成反比。

证明：可以求出，在一级价格拍卖中，投标人的预期收益是：

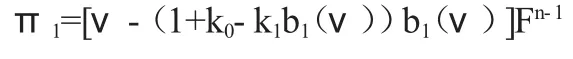
（21）从（20）式得到，π1与ν*成反比，所以，π1和r 成反比，和k0成反比，和k1成正比。

四、结论

文章考虑了一类带有线性佣金率k=k0-k1b 和保留价r 的拍卖模型。主要结论如下：

（1）收益等价定理在本模型中不成立，如果投标人数比较多，应该选择第二价格拍卖。卖者的预期收益和佣金系数k0负相关，但和k1正相关，和保留价r 也正相关。

（2）本模型与不考虑佣金时的情形相比较，卖者的预期收益变少了，而且,减少的部分是拍卖行的预期收益。拍卖行的预期收益和k0正相关，但和k1负相关。

（3）在本模型中，投标人在一级价格拍卖中获得更多的预期收益；二者均和k0成反比，和k1成正比，和r 成反比。

注释：

①Riley J G, Samuelson W F. Optimal auctions[J].American Economic Review, 1981, (3): 381- 392

②McAfee R P, McMillan J. Auctions and bidding [J]. Journal of Economic Literature, 1987, (2): 699- 738

③McAfee R P, McMillan J. Bidding rings [J]. American Economic Review, 1992, (3):579- 599

④王彦,毕志伟,李楚霖.佣金收取对拍卖结果的影响[J].管理科学学报,2004,(4):44- 48

⑤Wang Y, Commission strategy of the auction house[J]. Wuhan University Journal of Natural Sciences, 2006,(11):507- 510

⑥杨卫星，刘树林.带有线性佣金率的密闭式拍卖模型研究[J].统计与决策，2011(13):35- 38

⑦刘树林，杨卫星.第一价格密封拍卖中的最优保留价和最优佣金率研究[J].经济研究，2011,(11):145- 156

⑧冉茂盛，黄俊，李文洲.考虑佣金率的一口价拍卖模型[J].系统工程理论与实践，2016,(9):2276- 2283