信息不对称及广告效应下零售商损失厌恶的供应链协调
2020-03-19史文强孔昭君汪明月
史文强, 孔昭君+, 汪明月
(1.北京理工大学 管理与经济学院, 北京 100081;2.中国科学院大学 公共政策与管理学院, 北京 100049)
0 引言
广告在供应链市场竞争中承担着重要的角色,逐渐成为企业营销和品牌宣传的一项重要手段。我国广告经营总额从1990年的25亿元增长到2017年的6 896亿元,年复合增长率达到23.14%[1]。复杂的外界环境和激烈的市场竞争使销售企业不断加大广告投入、改善广告效果,以保障消费者充分了解产品信息,提升顾客的购买需求[2]。适当的广告投入能够增加销量,从而增加供应链整体效益,然而过量的广告费用也会带来额外成本,加重企业负担。因此广告投入策略是企业的一项重要决策,设计合适的广告策略对供应链各企业均有重要的意义。实际上,供应链决策者面对复杂的市场环境和决策条件时会有不同的风险偏好和心理认知,决策者更加关注的不再只是利润和绩效的最大化,而是产品缺货、库存积压、广告投资失败等引发的、易使其产生损失厌恶行为[3-5]的各种损失风险。另外,供应链系统由众多独立的决策主体构成,为了规避损失,各主体通常会隐藏私人信息(包括成本、需求、心理因素等),引发信息不对称问题,从而加剧双重边际效应,造成供应链系统低效[6]。因此,以参与者损失厌恶和信息不对称为前提,分析广告效应影响下的供应链协调机制,探索供应链的最优决策模式,是亟待解决的问题。
目前,已有许多学者针对广告效应对供应链决策的影响展开研究,杨宽等[7]考虑零售商负责广告促销,构建供应链库存管理模式下易损品的最优广告投入及最优价格联合决策模型,验证了广义收益共享契约能够实现供应链协调;马士华等[8]假设需求为广告投入的函数,分别构建了有无广告投入的二级供应链最优订货量和最优广告投入决策模型,并证明回购契约能够协调有广告投入的供应链;Ahmadi等[9]采用合作博弈和非合作博弈方法,分析了二级合作广告促销供应链模型的均衡解;易余胤[10]构建了广告影响市场需求的闭环供应链协调模型,探讨了产品回收率和广告分担率对供应链最优决策的影响;刘盼等[11]采用Stackelberg博弈构建了3种成本分担模型,分析了大数据环境下定向广告和消费者偏好信息投入对供应链企业定价决策的影响;Song等[12]考虑创新努力和广告支持对市场需求的影响,分别构建合作和非合作博弈模型,探讨了双向补贴政策对二级供应链的协调作用。然而,这些研究成果均未涉及信息不对称及零售商损失厌恶所产生的影响。
在供应链信息不对称方面,国内外也有许多学者从成本信息、需求信息等角度入手,采用契约设计的方法探讨如何应对信息不对称问题。成本信息不对称现象在医药、通信等制造业供应链中广泛存在[13]。Lei等[14]考虑供应商拥有私人成本信息,在需求随机条件下构建了零售商库存不精确的博弈模型,研究了不同情况下的供应链绩效和契约协调参数;吕方等[15]以双供应商和单制造商组成的装配系统为研究对象,考虑其中一个供应商成本信息不对称,分别探讨了批发价契约和价格补贴契约对系统的协调作用;金亮等[16]以在线离线/线上到线下(Online to Offline,O2O)供应链为对象,考虑线下体验店的体验服务成本信息不对称,运用委托代理理论设计线上零售商佣金契约,探索了不对称信息对供应链绩效的影响;刘浪等[17]考虑市场价格随机波动,采用数量折扣契约分别构建了销售成本信息不对称和生产成本信息不对称下的供应链模型,发现供应链中的跟随者能够从隐瞒私有信息中获利;Wang等[18]以供应商成本信息不对称为前提,设计了一组包含订单数量、转移支付、平衡参数的契约,发现在一定条件下该契约能够提高供销双方的利润;Kerkkamp等[19]以零售商保留成本信息不对称为前提,设计了一组包含附带支付的激励契约,探索了不同零售商类型下的二级供应链协调问题。还有许多学者针对需求信息不对称的影响展开了研究,例如Babich等[20]以突发事件影响市场需求为前提,运用回购契约研究了需求信息不对称下的二级供应链协调问题;Feng等[21]针对交易数量和价格,构建了需求信息不对称下的动态讨价还价模型,认为提高预测精度会使交易企业双赢;Li等[22]考虑市场需求为不对称信息,构建了零售商为损失厌恶者的双渠道供应链模型,分析了不对称信息对制造商最优生产量的影响;Zissis等[23]认为数量折扣契约可以协调需求信息不对称下的供应链;谢文明等[24]构建了需求信息不对称下具有直销渠道的二级供应链产能管理模型,设计产能预定合同以保证分销商向供应商传递真实信息;Lobel等[25]考虑零售商隐藏需求信息,设计了批发价契约和期权契约相结合的长期契约。更有一部分学者以需求信息和成本信息皆不对称为背景展开了研究,Lei等[26]在需求信息和成本信息不对称的情况下,构建了供应链扰动的风险管理策略,发现信息不对称下的最优生产量并不高于信息对称下的情况;张欢等[27]考虑生产成本信息和市场信息皆为私有信息,设计了批发价契约和销售奖惩契约下的供应链双边信息不对称激励模型。还有学者以质量信息不对称[28]、努力程度信息不对称[29]和公平关切信息不对称[30]等情况为背景,探索供应链最优运作机制。
如前所述,大部分现有成果在研究广告投入对供应链决策的影响时,是在信息对称前提下展开的;而有关供应链企业信息不对称的研究仍然集中在成本信息和需求信息的不对称情形,鲜有文献涉及决策者心理信息的不对称问题,如损失厌恶、风险偏好等信息不对称问题。另一方面,已有学者通过实验证明,影响决策过程的心理因素是决策主体的私有信息[31]。在供应链的实际运作过程中,主要由零售商担负广告促销任务,一旦广告投入无法有效提升市场需求,零售商将面临更大的风险。此时,零售商极有可能怀疑或否定自己对事件前景的预期,进而产生损失厌恶心理,并为了规避风险而隐藏自身的损失厌恶程度。
鉴于此,本文考虑零售商为损失厌恶者,假设市场需求是广告费的函数,构建零售商损失厌恶程度信息不对称条件下的广告费及订货量供应链联合决策模型,求解最优的订货及定价决策,探讨收益共享契约能否实现二级供应链的协调,并与集中决策、信息对称下的最优决策进行对比,分析批发价、损失厌恶程度、广告效应因子、市场价格等参数对供应链最优决策的影响。
1 问题假设与模型描述
考虑一个风险中性制造商和一个损失厌恶零售商组成的单周期二级供应链,制造商按成本cs生产一种短周期产品,零售商以批发价w引进q件该产品,并以价格p销售给消费者,零售商为吸引更多的消费者所耗费的广告费为u;期末剩余产品按残值v进行处理,若存货不足,则零售商和制造商分别按每单位gr和gs支付缺货成本,g表示供应链整体的缺货成本。
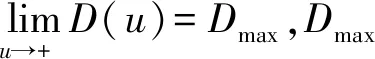
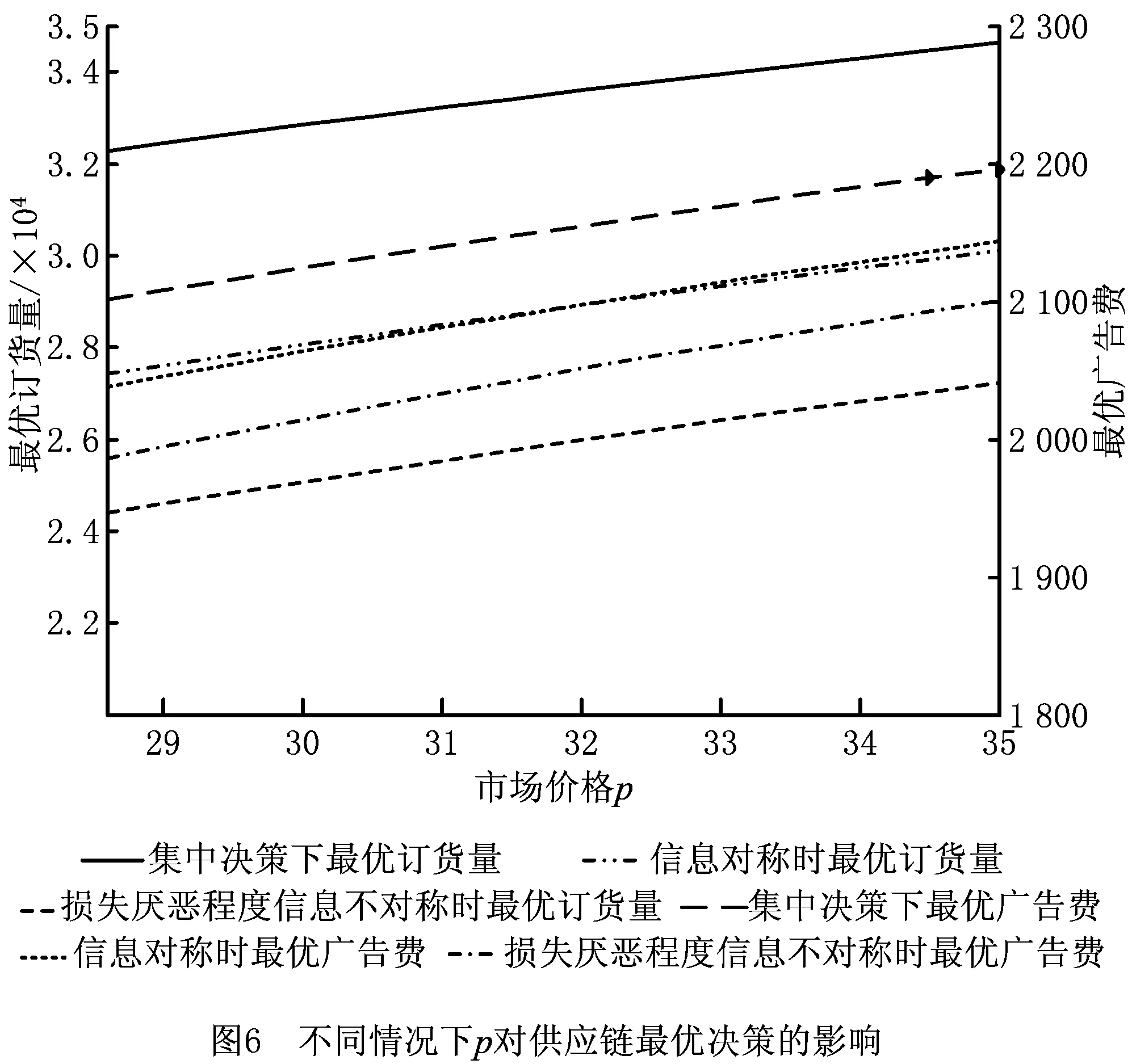
上述参数应满足v 采纳文献[4,33]中的分段线性函数描述损失厌恶对零售商期望效用的影响,零售商的期望效用函数为 (1) 首先给出集中决策下供应链的最优订货量和最优广告费联合决策模型。作为一个整体共同决策,集中决策模式下的制造商和零售商信息共享且不存在风险态度。集中决策下供应链的利润函数为 (2) 对应的集中决策下的期望利润为 结合上述表达式,可将式(3)转化为 此时供应链的核心问题是求解最优的订货量和广告费,以保证供应链的期望利润最大化。 首先,令u为常量,对式(4)求关于q的一阶、二阶偏导: (5) (6) 其次,令q为常量,对式(4)求关于u的一阶、二阶导数: (7) (10) 在分散决策模式下,损失厌恶的零售商和风险中性的制造商均为独立的经济实体,每一方将以自身利益最大化为目标进行订货及生产决策。零售商和制造商在销售周期内达成如下收益共享契约:零售商销售产品取得利润后,将φ比例的收入转移给制造商,自己仅保留1-φ的收入,并以较低的批发价格购买产品(φ在这里也可以为负值)。 分散决策时零售商的利润为 (11) 综上可知,当市场需求低于qA或高于qB时,零售商将面临一定的过量或缺货损失;若将市场需求量控制在[qA,qB]范围内,则零售商将获得收入。因此,当[qA,qB]范围增大时,零售商面临的风险会减小。 根据式(11)可得零售商期望利润函数 将命题1所求的两个盈亏平衡点代入式(12),可得零售商在D(u,ε)≤q,D(u,ε)>q两个阶段的期望损失函数 D(u)·x)-wq-u]f(x)dx; -wq-u]f(x)dx。 零售商的期望收入函数为 [pq-gr(D(u)·x-q)-wq-u]f(x)dx。 其中零售商的期望利润为期望收入与期望损失之和,即πr=Wr1(q,u)+Wr2(q,u)+G(q,u)。 考虑收益共享契约和损失厌恶程度后,得到的零售商期望效用函数 U(πr)=(1-φ)G(q,u)+λ(Wr1(q,u)+ Wr2(q,u))=(1-φ)πr+(λ-1+φ) (Wr1(q,u)+Wr2(q,u))。 (13) 风险中性制造商的利润为 (14) 因为制造商期末将获得零售商的收入分成,所以制造商的期望效用函数为 f(x)dx+φG(q,u)。 (15) 在信息对称条件下,零售商的损失厌恶程度λ为共享信息。销售季节开始前,制造商作为主导方提供一份契约{q,u,φ}供零售商选择,该契约为一组菜单式合同,是一种自我选择的合约机制,合同的主要内容包括订货量q、广告费u和收益共享系数φ。零售商仅可选择“接受”或“拒绝”契约(take it or leave it),而不能自主改变契约参数。 信息对称时,制造商知道损失厌恶程度λ的准确信息,供应链的目标函数和约束可表示为: s.t. U(πr)=(1-φ)πr+(λ-1+φ) (17) 整理式(16),得到收益共享系数 (18) 将其代入供应链目标期望效用,可得 (19) 证明对式(19)求关于q的一阶、二阶偏导数,判断是否存在最优解使目标效用最大。 (20) 同理,对式(19)求u的一阶、二阶导数,化简得到: (g-gr+λgr)μD″(u)+(λ-1)·{D″(u)· (21) 将式(20)和式(21)联立,即可同时解得信息对称时供应链的最优订货量和广告费。将qs*和us*代回式(18)得到φ=1+{λ[Wr1(qs*,us*)+Wr2(qs*,us*)]}/G(qs*,us*)。证毕。 根据命题2求得的qs*和us*代入式(19)可得最优的制造商期望效用 S(qs*,us*))+G(qs*,us*)+λ[Wr1(qs*,us*)+ Wr2(qs*,us*)]。 (22) 性质1零售商为损失厌恶者:①当D(u)≤D′(u)[(w-v)q+u]时,最优订货量qs*随最优广告费us*的增加而增加;②在一定条件下,最优订货量qs*和最优广告费us*随损失厌恶系数λ单调递减。 证明 (1)求式(20)关于u的偏导数 (23) (24) (2)首先判断us*与损失厌恶程度λ的关系。 (25) (26) 其次,根据隐函数求导定理判断qs*与λ的关系。 qs*是us*和λ的函数,而us*是λ的函数,因此qs*可以表示为q(us*(λ),λ),对q(us*(λ),λ)求关于λ的一阶导数可知 (27) 对式(20)等式两边求关于λ的隐函数导数,可得 (28) 性质1说明,零售商为损失厌恶者时,其最优订货量和最优广告费均低于零售商为风险中性的情况。其管理学意义是,随着损失厌恶程度的增加,制造商往往设计谨慎的订货和促销策略供零售商选择,以此控制盈亏平衡点的范围,降低缺货和过量风险。 3.2.1 信息不对称时供应链的最优订货和广告策略 零售商传递虚假信息时的期望效用函数为 (29) 当零售商接受收益共享契约并报出真实损失厌恶程度时,制造商的期望效用 f(x)dx+φ(λ)·G(q(λ),u(λ))。 (30) 根据Myerson显示机理,需要设置最优机制保证零售商如实报出损失厌恶程度。制造商设计的机制如下: S(q(λ),u(λ)))+φ(λ)·G(q(λ),u(λ))]h(λ)dλ。 (31) (32) (33) 证明根据零售商期望效用的含义,可得 (34) Wr2(q(λ),u(λ))]=0。 有 Wr2(q(λ),u(λ))]<0。 (35) (36) 证毕。 由此可见,损失厌恶程度越大,零售商获得的期望效用越少。 根据零售商期望效用的定义及命题3,求得信息不对称时收益共享系数 Wr2(q(λ),u(λ)))}/G(q(λ),u(λ))。 (37) 将U(πr(λ))和φ(λ)代入制造商的期望效用函数,求得全新的目标函数为 μ-S(q(λ),u(λ)))+G(q(λ),u(λ))+λ[Wr1(q(λ), u(λ))+Wr2(q(λ),u(λ))]-U(πr(λ))}h(λ)dλ (38) 命题4零售商损失厌恶程度为不对称信息时,供应链有唯一的最优订货量qa*、最优广告费ua*和收益共享系数φa*。 证明为了使制造商的目标期望效用最大,本质上只要选择一个qa*和ua*使得式(39)最大化。 (39) 式(39)为式(38)积分号内部的表达式。 根据q,u的一阶最优条件可得: 根据u的一阶最优条件可得: (40) (41) 将式(40)和式(41)的解代入式(37)可求得最优收益共享系数φa*。证毕。 3.2.2 损失厌恶程度信息不对称下的供应链协调机制分析 命题5当广告投入会影响市场需求,且零售商损失厌恶程度信息不对称时,适当调整批发价w即可实现广告效应下的供应链协调。 (42) 通过式(42)可知,协调的最优策略不受损失厌恶程度λ的影响。证毕。 3.2.3 信息不对称下最优决策的敏感性分析 本节分析信息不对称下最优订货量和最优广告费随各参数变化的情况。 性质2当D(u)≤D′(u)[(w-v)q+u]时,最优订货量qa*随最优广告费ua*的增加而增加。 证明当D(u)≤D′(u)[(w-v)q+u]时, (43) (44) 证毕。 由此可知,广告投入越多,最优订货量也越多。广告费用的增加将直接刺激市场需求规模,供应链唯有制定较高的订货策略才能响应增长的需求,避免缺货损失。 性质3当考虑批发价为市场所决定的外生变量时,qa*和ua*均为批发价w严格的减函数。 证明考虑w为市场决定的外生变量,重点判断改变批发价对分散决策供应链最优策略的影响。ua*可由w表示,qa*是ua*和w的函数,qa*可表示为q(ua*(w),w),因此根据隐函数定理对q(ua*(w),w)求w的一阶导数可知 (45) (46) (47) 对式(40)隐函数求w的导数,得到 (48) 性质3说明,当批发价增加时,零售商每订购一单位产品将付出额外的费用,零售商将失去订货的动力,表现为供应链的最优订货量和最优广告费用均减小,此时制造商将设计一组谨慎的订货和广告策略菜单,在控制市场需求的同时保障零售商参与合作。 性质4在一定条件下,qa*和ua*随损失厌恶系数λ的增加而减少。 证明qa*是ua*(λ)和λ的函数,qa*可表示为q(ua*(λ),λ),故对q(ua*(λ),λ)求λ的一阶导数可知 (49) 并求得 (50) 对信息不对称下供应链最优订货量的表达式(40)求λ的隐函数导数,可得 (51) 综上所述,随着零售商损失厌恶程度的增加,供应链最优订货量和广告费都减小。在面临同级别的损失时,损失厌恶程度大的零售商更容易产生明显的抵触心理,作为供应链主导方的制造商将调整菜单式契约,严格控制订货量和广告费,降低零售商面临的损失风险。 性质5信息不对称时,最优订货量qa*和最优广告费ua*随零售价p单调递增。 然后求得 (52) 对式(40)求关于p的隐函数导数,可得 (53) 3.2.4 信息不对称对供应链最优决策的影响 本节将信息对称与信息不对称的模型进行对比,分析损失厌恶程度信息不对称对供应链最优决策的影响。 证明 (1)可将式(20)和式(40)分别变换为: =λ-1; (54) (55) (2)结合U(πr)=0和式(36),易得 U(πr(λ))a*-U(πr)s*= 证毕。 性质6说明损失厌恶程度信息不对称会影响供应链的最优订货和广告决策,进而降低供应链的整体绩效;即便是信息对称,供应链最优订货量和广告费仍不会高于集中决策的情况。 先设定批发价为外生变量(w=12),求解一般情况下供应链的最优决策;再将批发价w视为内生变量,观察调整批发价对供应链的协调作用。 表1表示信息不对称下供应链协调时的最优决策量和各节点期望效用。当批发价恒定不变时,分散决策下的供应链最优订货量、最优广告费和供应链期望效用均低于集中决策时,供应链无法协调;当损失厌恶程度为不对称信息时,若调整批发价为2.925,则能使供应链协调,此时供应链信息不对称下的最优订货量32 843、最优广告费2 124.18和供应链期望效用231 762.31均与集中决策一致,满足协调的判断条件。为了达成供应链协调的目标,需要大幅降低批发价,调整后的批发价甚至低于生产成本(收益共享契约允许批发价低于生产成本)。同时,为了保证制造商利润不受损害,需将收益共享系数大幅调高为0.914 655。零售商期望利润301 118.71远大于非协调时的52 865.97,零售商面临的期望损失降低为0。另外,采用调整后的契约不但零售商和制造商的期望效用均不会降低,而且供应链整体期望效用得到提升,实现了互惠共赢。其管理学含义为:零售商隐藏损失厌恶程度的行为对供应链系统效益造成影响,制造商需要设计一组订货量、广告费和收益共享系数的组合式契约激励零售商报出真实信息,同时降低批发价来提升供应链的渠道效率。当批发价减小到一定程度时,零售商面临更小的损失风险,其愿意接受更积极的订货和促销策略,以获取高额利润。同时,制造商在设计的合约菜单中将通过大幅提高零售商的收益共享系数来弥补批发价降低对自身造成的损失,通过合理调整批发价加强供应链产销双方的合作,从而提升供应链的整体运作效率,使供应链系统达到协调。 表1 信息不对称时的供应链协调决策 假定供应链的其他参数恒定不变,观察批发价w变化对供应链最优决策和各节点企业期望效用的影响,相应的数值如图1、图2和表2所示。 根据图1和图2可知,无论在何种信息下,最优订货量、最优广告费、供应链整体期望利润和期望效用均随批发价的增加而降低;信息对称下的最优订货量、广告费和供应链期望利润大于信息不对称时,但小于集中状态下的最优决策;信息共享有效提升了供应链的决策效率,然而分散决策仍然无法达到集中决策下的最优;供应链的期望效用总低于供应链的整体期望利润,这是因为损失厌恶零售商对损失更加敏感,较小的损失会令其产生较大的损失效用。 由表2可见,不论在何种信息模式下,若w减少,则零售商的期望利润、零售商的期望收入、制造商的期望效用、收益共享系数φ和盈亏平衡点qB都将增加,零售商的期望损失和盈亏平衡点qA随w的减少而减少;信息不对称时,零售商的期望效用随批发价增加而单调递增。增加批发价不但直接降低了零售商单位利润,而且缩小了零售商的盈亏平衡点范围[qA,qB],增加了其面临的缺货和过量风险。当面临更大的损失可能性时,零售商更倾向于接受保守的订货策略;制造商制定菜单式合同时,将通过适当减少广告投入来控制市场需求,防止出现缺货。增加批发价并减少订货量和广告费会降低零售商的期望收入,微薄的收入导致零售商只能接受更低的收益共享系数;保守的促销、订货手段和收益共享比例给制造商带来的损失超过增加批发价带来的收益,因此制造商的期望利润和批发价成反比。 信息不对称下,盈亏平衡点qA和qB、零售商期望损失、收益共享系数φ及制造商的期望效用都低于信息对称的情况,而零售商的期望利润、零售商期望收入及零售商的期望效用均比信息对称时要大, 表2 不同信息状态下w对供应链各节点企业参数的影响 续表2 其管理学意义为:信息不对称时,保守订货和广告促销的策略降低了盈亏平衡点qA,从而控制过量损失,使零售商期望收入增加;同时,制造商为了促使零售商报出真实信息,将减少收益分享的比例。 假设批发价为固定值(w=12),分别做出最优订货及广告策略、供应链期望利润及效用、各节点企业的期望效用、收益共享系数等变量关于损失厌恶程度λ的变化趋势图表,如图3、图4和表3所示。 根据图3、图4和表3可知,无论产销双方是信息共享还是信息不对称,供应链最优订货量、最优广告费、盈亏平衡点qA和qB、零售商的期望损失、零售商的期望效用、供应链整体的期望利润和效用均随λ的增大而减小;而零售商的期望利润、零售商的期望收入、收益共享系数均随λ的增大而增大。信息不对称时,λ增大将会导致制造商期望效用先增大后减小。损失厌恶程度越高,零售商对损失越敏感,制造商将会设计一个有低额广告投入的菜单来调控市场需求,防止发生零售商缺货损失,进而降低订货量。在其他条件不变的情况下,保守的订货和促销策略能有效将盈亏平衡点控制在合理的范围内,从而减小零售商的期望损失,同时为弥补订货量减少带来的损失,制造商将设计高额的收益共享系数。制造商受最优订货策略和收益共享系数的双重影响,当收益共享系数增大的作用较大时,制造商的期望效用将小幅增加,而当订货量减少造成的影响较大时,制造商的期望效用将呈现随损失厌恶程度递减的趋势。 无论λ为何值,集中决策下的最优订货量、最优广告费和供应链期望利润大于信息对称和信息不对称时的情况,而且λ越大,上述各决策模式下变量的差距也越大。这说明集中决策的效率高于分散决策(信息对称和信息不对称),损失厌恶程度越大,零售商对损失的抵触情绪越强,决策效率的差异体现得越明显。 表3 不同信息状态下λ对供应链各节点企业参数的影响 信息不对称下的盈亏平衡点、零售商的期望损失、收益共享系数和制造商的期望效用均小于信息对称时,而零售商隐藏信息的行为会使其期望利润、期望收入和期望效用增大,这一规律与4.2节类似。 本节将批发价固定为w=12,损失厌恶程度λ=1.2,观察广告效应因子α在[0,0.02]范围内波动时供应链最优决策和各节点效用的变化情况,如表4、图5和表5所示。 根据表4和图5可知,在集中决策、信息对称和信息不对称3种决策模式下,最优订货量、供应链的期望利润和期望效用均与α满足同增同减的关系,且随着α增大,其变化幅度减小;最优广告费却与α呈现单调递减的关系,而且α越大,广告费u变化的幅度越小。其经济学含义为:广告效应因子越大,市场对广告投入的反响越强,往往极小的广告费用即能产生大量的市场需求;当广告效应因子足够大时,随着α增加,效用变化量递减。 由表5可见,无论产销双方信息状态如何变化,盈亏平衡点qB、收益共享系数、零售商的期望收入、零售商的期望利润和制造商的期望效用均与α正相关,而盈亏平衡点qA、零售商的期望损失与α负相关。信息不对称时,零售商期望效用随α单调递减。其管理学意义为:广告效用因子增加使市场需求激增,供应链主导方通过设计积极的订货策略和保守促销策略来响应市场需求,二者作用使盈亏平衡点的范围增大,从而降低零售商面临的期望损失,提升零售商获益的可能性,同时零售商愿意接受更大的收益共享比例,促使制造商降低批发价,以进一步抢占市场份额。 表4 不同决策模式下α对供应链最优决策的影响 表5 不同信息状态下α对供应链各节点企业参数的影响 当w=12,λ=1.2时,令α=0.003,市场价p波动,探索供应链的最优决策和各节点效用的变化规律,如图6、图7和表6所示。 由图6、图7和表6可见,无论p取何值,集中决策下的最优订货量、最优广告费和供应链的期望利润总是最大,信息对称情况次之,信息不对称时最小。无论何种决策模式,随着p的增加,供应链的最优订货量、最优广告费、供应链系统的期望利润和效用都会增大。 在分散决策模式下(信息对称和信息不对称),盈亏平衡点qB、收益共享系数、零售商的期望收入、零售商的期望利润和制造商的期望效用与p正相关,而盈亏平衡点qA与p负相关。特殊的是,在信息对称条件下,零售商的期望损失随p的增加而递减;当信息不对称时,p增加会导致零售商的期望损失增加。 本文在市场需求受广告影响且零售商为损失厌恶者的情况下,使用“前景理论”和“显示机理”构建了损失厌恶程度为不对称信息时收益共享契约下的订货量和广告费联合决策模型,分析了批发价、损失厌恶程度、广告效应因子、市场价对供应链最优决策的影响,探讨了供应链的协调情况,并与集中决策和信息对称模式下的最优决策进行对比,最后用数值分析进行验证。研究得出以下结论: (1)无论信息对称还是信息不对称,最优订货量、广告费和供应链的期望效用均随批发价的增加而递减,与市场价格正相关,在一定条件下与损失厌恶程度负相关。这是因为增大批发价会降低零售商的单位利润,零售商在面临更大的损失时,更倾向于 表6 不同信息状态下p对供应链各节点企业参数的影响 接受保守的订货策略,进而通过控制广告投入来降低市场需求,防止缺货损失;增加损失厌恶程度会直接放大零售商对损失的感知,在面临更大的风险时,零售商更容易接受保守的订货和促销策略,进一步导致供应链的整体利润受损;较高的市场价格会增加零售商的单位利润,促使零售商接受积极的订货和广告策略。 (2)较为特殊的是,无论处在何种信息状态,随着批发价的增加,制造商的期望效用都会不升反降,这与以往的广告效应下供应链文献[8]得出的结论有较大不同,可能的原因是在综合考虑损失厌恶和收益共享的情况下,增加批发价会缩小盈亏平衡点范围,导致零售商面临的风险激增;零售商只能接受较为保守的订货和广告策略,不但影响自身利润,而且会相应地降低收益共享比例。此时,制造商提升批发价所带来的效用增量已经无法弥补来自订货量、广告费和收益共享比例三者的抑制作用,制造商利润受到影响。这与实际情况相符,许多制造企业更愿意采用“薄利多销”策略来获取更多利润。 (3)在集中决策和分散决策模式下,最优订货量随广告效应因子的增加而递增,但增长趋势逐渐减缓,而最优广告费却与广告效应因子负相关,而且广告效应因子越大,广告费的降低趋势越平缓。这一结论与以往的文献也不同[10],已有文献往往认为广告效应因子越大,投入的广告费越多。本文在前人的基础上,综合考虑损失厌恶程度和缺货损失,供应链成员不再只关心利润最大化,更关注各种损失风险。此时,广告效应因子越大,市场需求对广告投入越敏感,零售商仅需投入少量的促销费用即可达到理想的效果,这时零售商愿意接受积极的订货策略响应市场需求。若利用广告效应的优势盲目增加广告费用来刺激市场需求,则很可能出现供不应求的情况,届时缺货损失和广告费用的双重压力会加大零售商的损失风险。订货量和广告费的变化速率随着广告效应因子的增大而减小,这种变化趋势体现了经济学中“边际效用递减”的规律。 (4)当广告投入影响市场需求时,集中决策下的最优订货量、最优广告费和供应链的期望效用最大,信息对称情况次之,信息不对称时最小。在损失厌恶程度信息不对称时,制造商和供应链的期望效用均低于信息对称时,而零售商的期望效用却比信息对称时要大。由此可见,信息共享模式虽然能大幅度提升供应链的决策效率,保证供应链利润优于信息不对称模式,但是仍低于集中决策下的最优策略;零售商隐藏损失厌恶程度信息虽然能使自身获得超额利润,但是影响了制造商和供应链的整体效率。 (5)在损失厌恶程度信息不对称时,适当调整批发价能够使分散决策下的最优订货量、最优广告费分别与集中决策下供应链的最优订货量和广告费相等,即供应链协调。实际上,若产销双方协商降低批发价格,并提升收益共享系数,则可以保障信息不对称的各方效用都不会减少,而且能提升供应链的整体效用,达到供应链的最优化,这一结论比以往的文献有了一定提升,目前已有学者运用不同契约讨论了广告效应下供应链的协调问题[7-8,10,34],也有学者证明了收益共享契约可以实现零售商谎报信息下的供应链协调[35],然而鲜有学者考虑损失厌恶信息不对称和广告效应对供应链协调运作的影响。部分学者研究了损失厌恶和广告效应情景下的报童模型最优订货和定价问题[32],但仅考虑了单个零售商的决策机制,并未分析供应链企业间的竞合博弈,更没有分析其协调问题。本文在前人研究的基础上,考虑损失厌恶信息不对称可能会影响广告效应下供应链的协调机制,阐明了收益共享契约下供应链协调的条件。 然而,作为一项系统研究的开端,为突破关键环节,本文仅考虑了具有单制造商和单零售商的供应链,也只分析了一方具有损失厌恶态度的情形,后续将研究多个零售商和制造商通过订货和广告决策进行博弈,以及信息不对称下供应链各节点企业皆为损失厌恶者的情况。
2 供应链集中决策模型
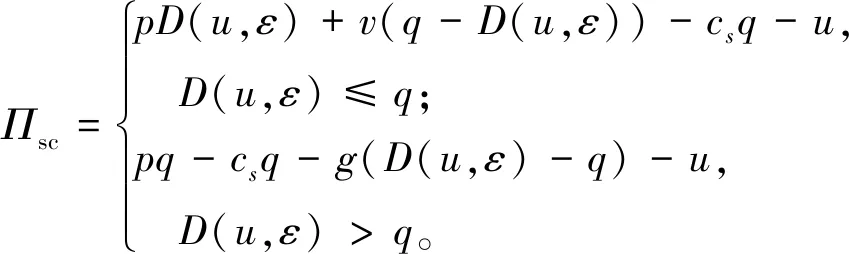
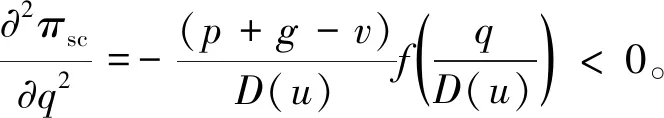
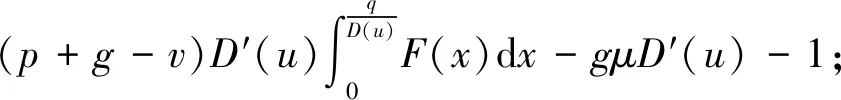
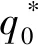
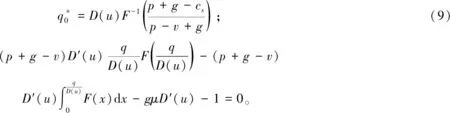
3 分散决策下损失厌恶零售商的收益共享契约模型
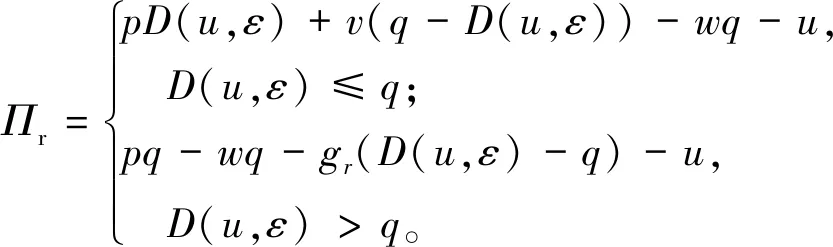
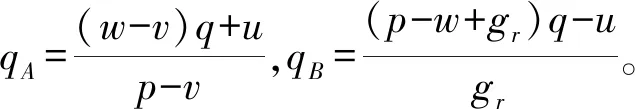
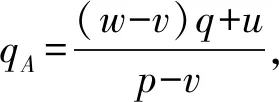
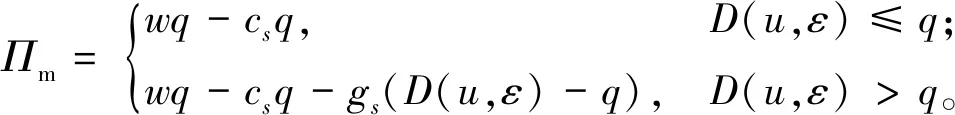
3.1 信息对称下的收益共享契约模型

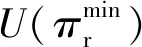



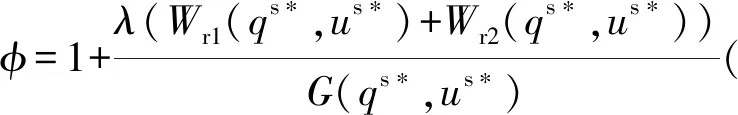


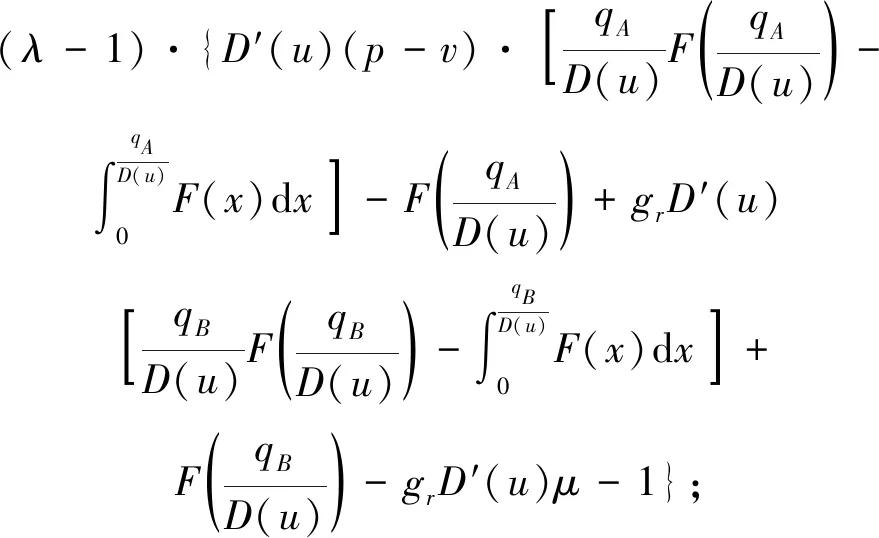
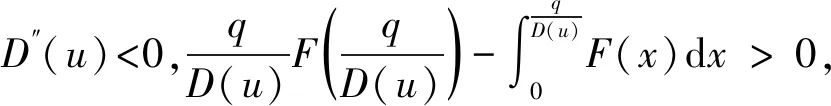

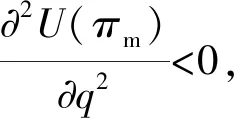
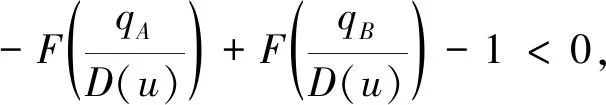
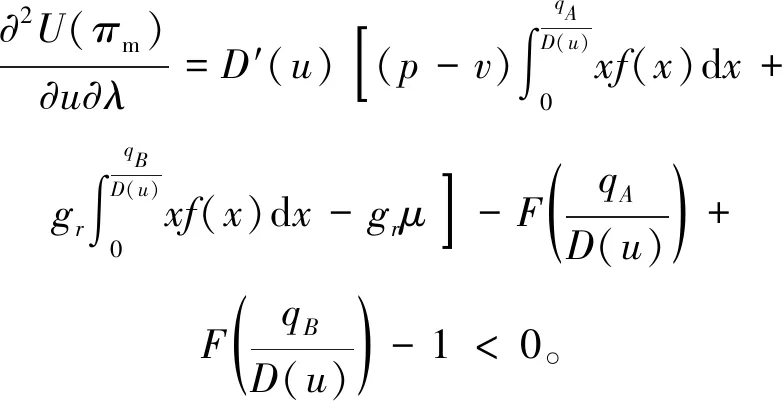
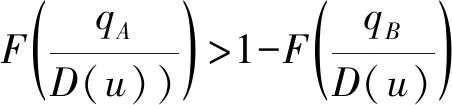

3.2 损失厌恶程度信息不对称下的收益共享契约模型
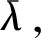


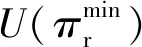
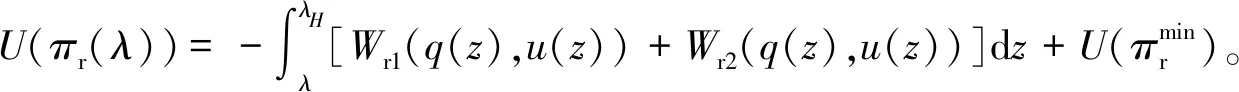
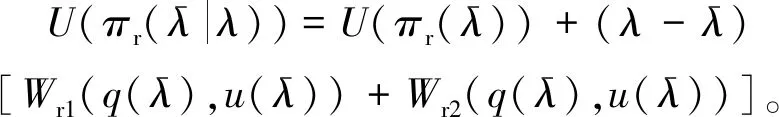


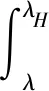
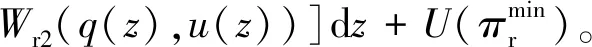
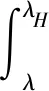



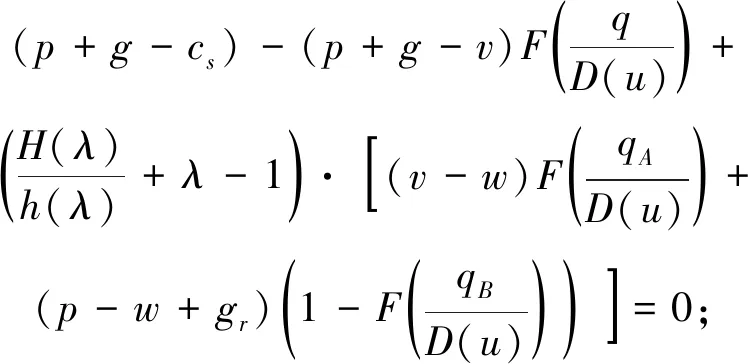

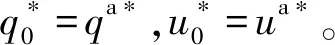
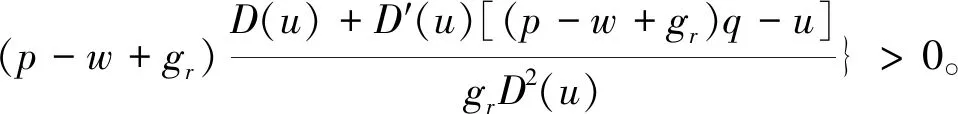


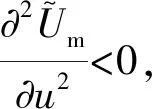

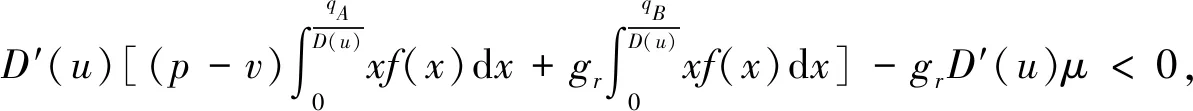


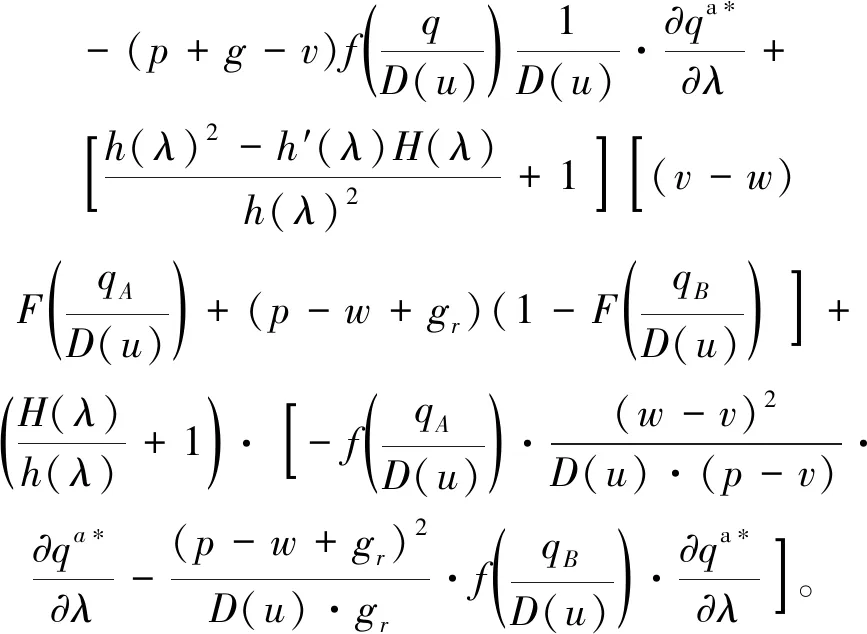

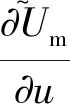
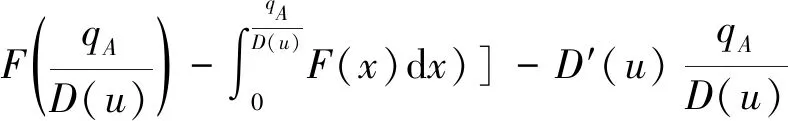

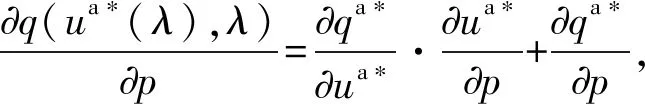



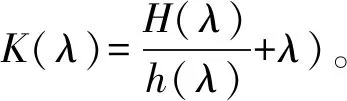
4 算例分析
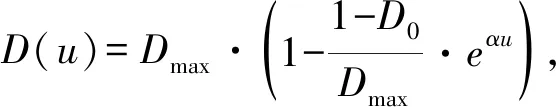
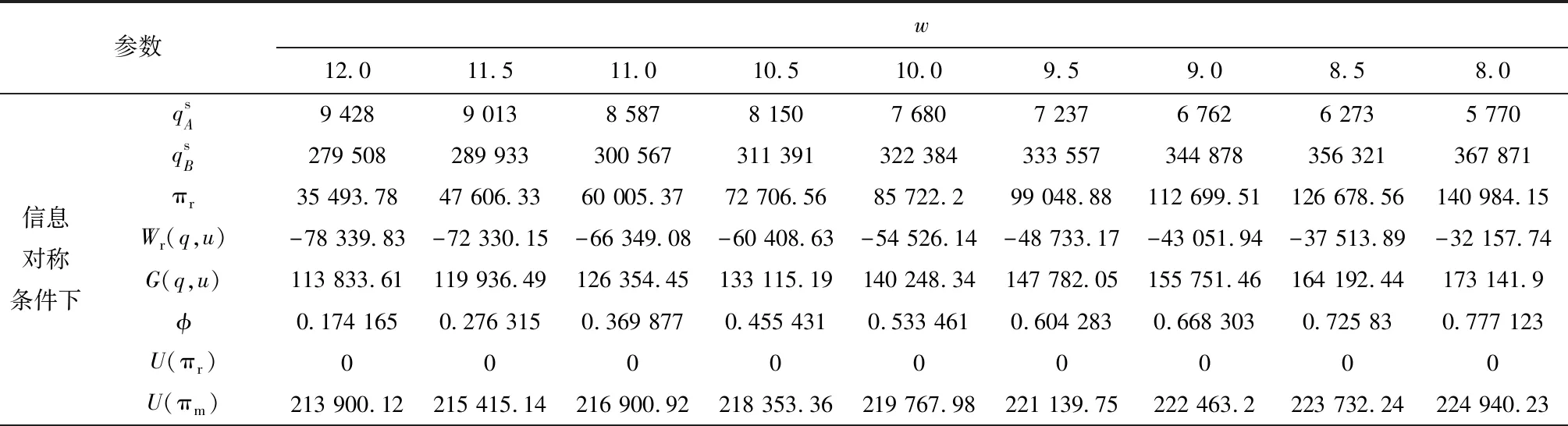
4.1 供应链协调分析

4.2 批发价对供应链的影响

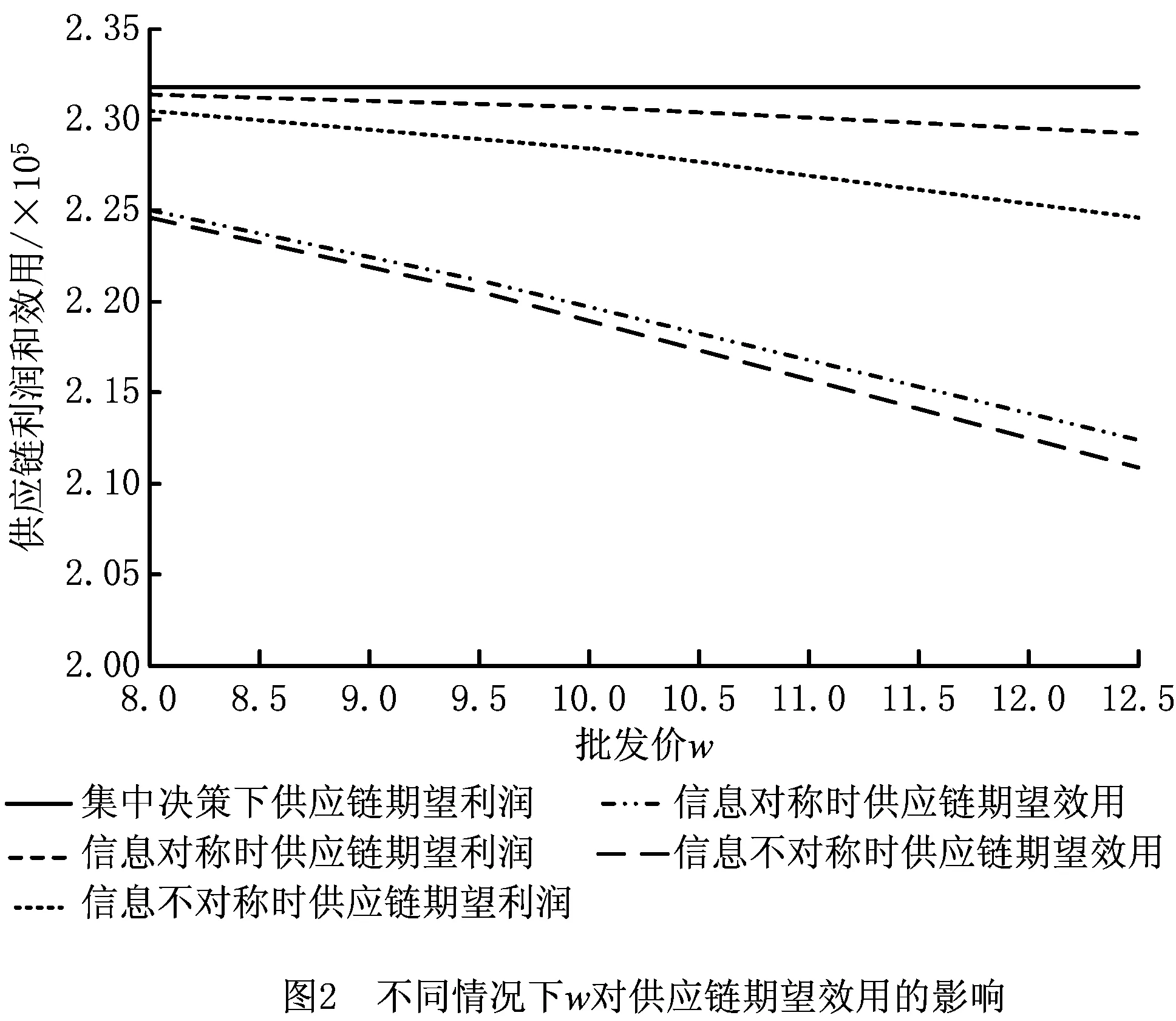

4.3 损失厌恶程度对供应链的影响

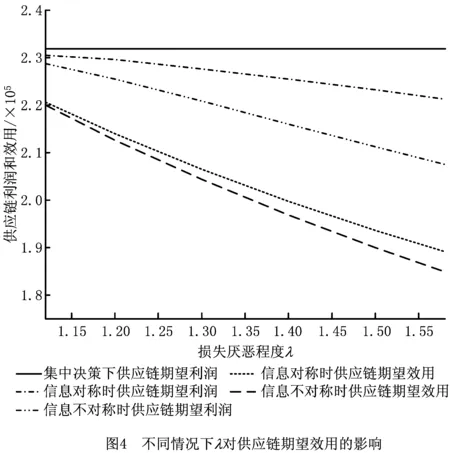

4.4 广告效应因子对供应链的影响

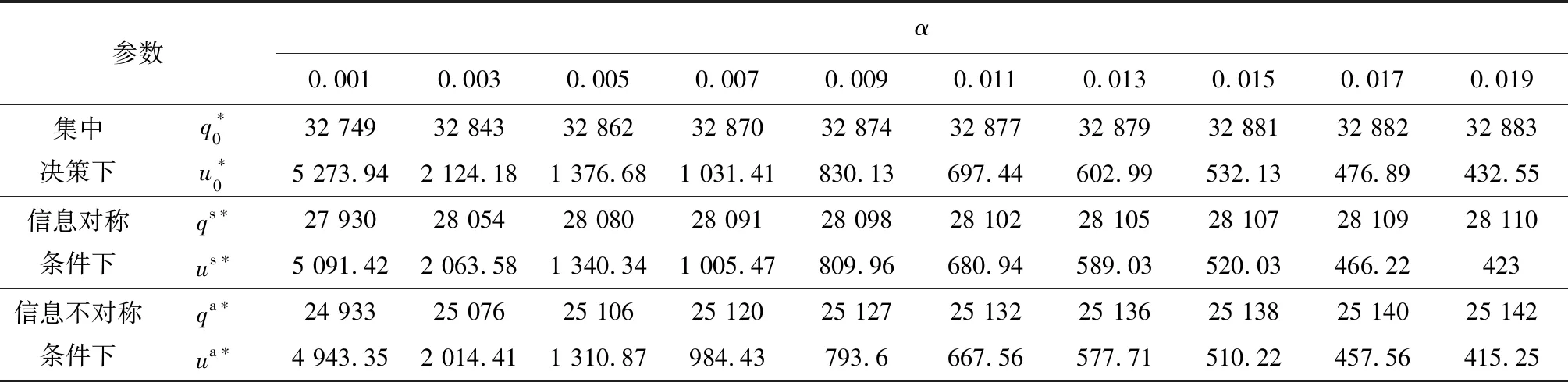
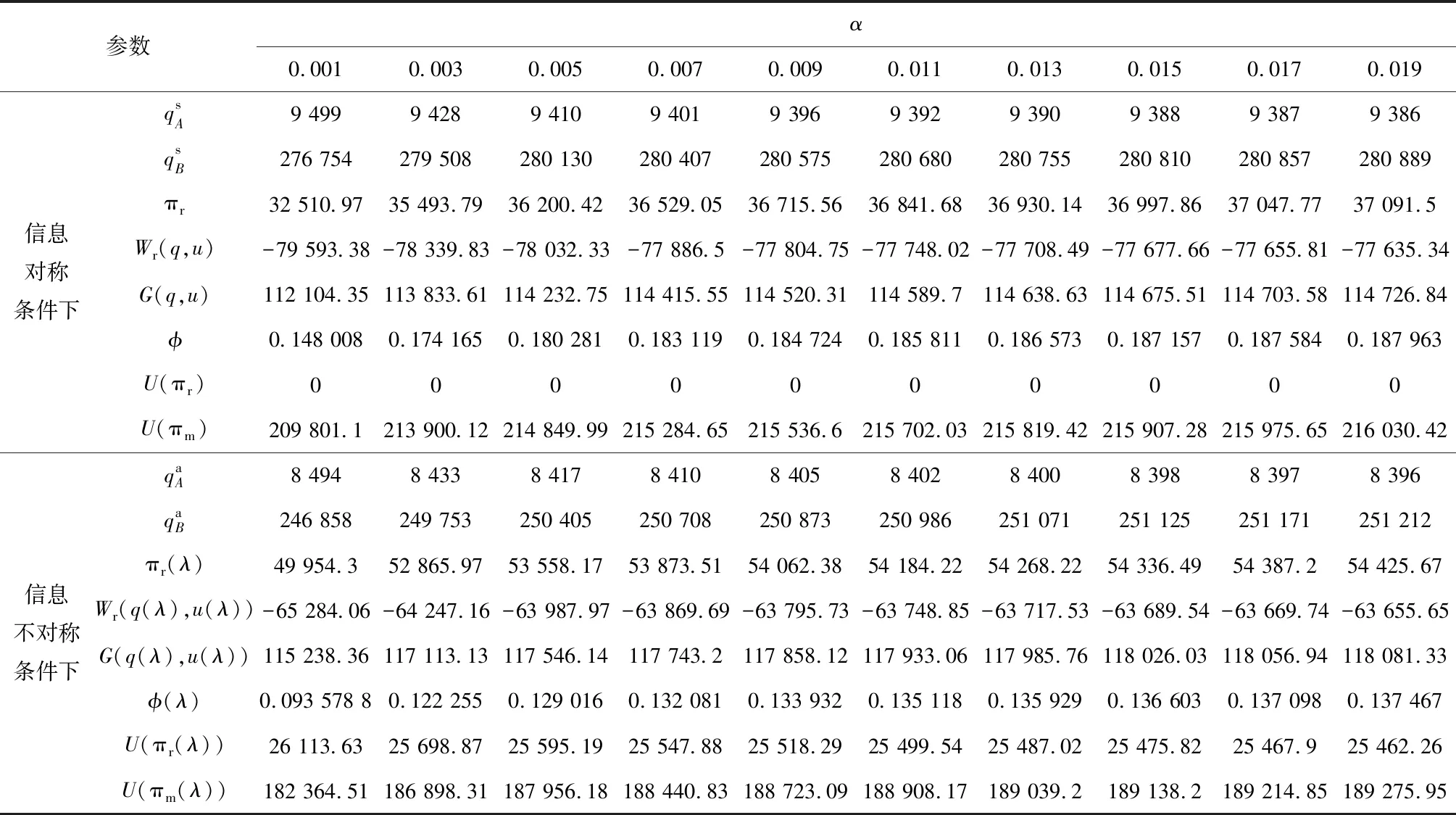
4.5 市场价格对供应链的影响

5 结束语