求解包含复杂关联约束的JSSP的二级嵌套混合算法

罗亚波， 余晗琳

(武汉理工大学机电工程学院，湖北 武汉 430070)

作为一种需满足设备和工艺复杂约束条件的组合优化问题，作业车间调度问题(job shop scheduling problem，JSSP)是典型的NP-hard问题，难以用传统优化方法求解。如何可靠、高效地求解JSSP已成为组合优化领域的研究重点和热点[1-3]，并已取得较多成果[4-7]。

目前作业车间调度常用的方法有基于规则的启发式算法[5]、遗传算法[6]、蚁群算法[7]、粒子群算法[8]、蜂群算法[9]以及将各种算法机制相结合形成的混合算法。其中，遗传算法与蚁群算法是应用较多的2种算法。遗传算法主要通过改进编码方式或改进适应度设置方法来进行优化[10-12]，如 DRISS等[13]提出一种采用新的染色体表达方式的遗传算法，并在一系列基准数据集的基础上进行了验证。蚁群算法主要有一阶变量和二阶变量2类或衍生改进的算法。如ZHAO等[14]提出了用于处理路线决策和任务排序的两代帕雷托蚁群算法。混合算法通常是将另一个算法的机制融合到主算法中[15]，并对主算法进行改进[16]，如混合遗传算法[17-18]。虽然这些算法在求解 JSSP方面有较多成果，但也存在一定的局限，如调度规模较小[19]、工序关系主要以串行为主等，对存在并行、甚至嵌套关系的复杂关联约束调度问题，研究还比较少。

当 JSSP规模较大且存在复杂关联约束时，解空间的复杂度呈几何级数上升，这种情况下，即使寻找可行解也有较大的困难。为此，依据 JSSP包含“设备分配”和“工序排序” 2个相互耦合的子问题的特征，本研究构造将遗传算法与蚁群算法集成到一个完整循环体的二级嵌套混合算法，以在可接受的迭代次数内求得比较满意的调度方案，增加搜索效率和收敛可靠性。

1 二级嵌套模型及其基本思路

为了能采用混合算法求解复杂关联约束问题，首先，从二级嵌套的角度构造包含复杂关联约束的JSSP的数学模型。

以任务工序与设备的关联关系的图1为例，共有4项独立的任务，每项任务均包含串行和并行的工序关系，共 33道工序，调度的目标是：将这些工序合理地分配到A (A1，A2)，B (B1，B2，B3)，C (C1，C2) 3类共7台设备上，使得总加工时间最短。与每一道工序相关联的有：前序工序、工序所需设备、工序时间。需要满足的约束包括：

(1) 前序工序约束。某工序启动前必须完成其他工序，且必须完成的工序完成后就一定能启动某工序，将必须预先完成的工序称为某工序的前序工序。如工序309，其前序工序为307和308，即：307和 308都完成了，就(才)可以启动工序309。

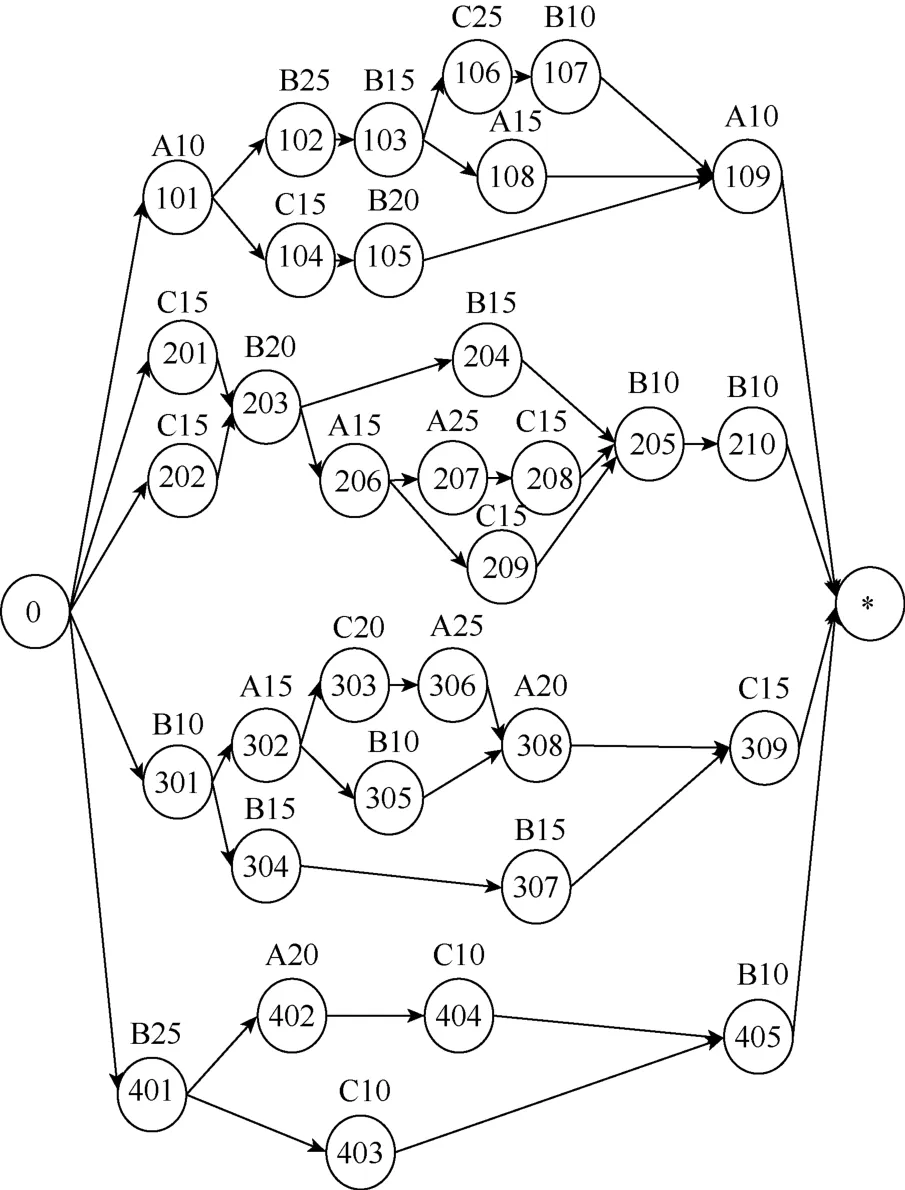
图1 任务工序与设备的关联关系示例图

(2) 设备匹配约束。工序必须分配到与之对应的加工类型的设备上，如各式机床、热处理设备等。在图中用字母A，B，C表示3类不同的设备，如工序401必须分配至B类设备上，即B1，B2，或者B3上。

(3) 工件独占约束。在同一时间，单一工件只能有一道工序处于加工状态。

(4) 设备独占约束。在同一时间，单一设备上只能有一道工序处于加工状态。

二级嵌套模型，即将问题分解为2个互有信息交换的子优化模型，分别求解工序的设备分配与工序在设备上的排序。假设作业车间系统中，有m台设备，n道工序，则优化模型如下：

一级：设备分配

求En(En表示各工序的设备分配方案)

MinC=Min{max(Bj+Tj)}

(j=1,2,···,m)

s.t

Ei=Ri(i=1,2,···,n)BE(i+1)j-BEij≥SEij

(i=1,2,···,n；j=1,2,···,m)

其中，C为第j台设备后道工序启动时间；Bj为第j台设备启动时间；Tj为第j台设备从启动到关停的时间；Ei为第i项工序的设备分配方案；Ri为第i项工序所需的设备类型；BE(i+1)j为第j台设备上排列的第i+1项工序的开始时间；BEij为第j台设备上排列的第i项工序的开始时间；SEij为第j台设备上排列的第i项工序的标准工时。

二级：工序排序

求Pn(Pn表示各工序在所分配设备上的排序)MinCEn= Min{max(BEnj+TEnj)}

(j=1,2,···,m)

s.t

Bik-Bi≥Sik

(i=1,2,···,n；k=1,2,···,i)BE(i+1)j-BEij≥SEij

(i=1,2,···,n；j=1,2,···,m)

Bi(qr)+Si(qr)≤Bi(q(r+u))

其中，CEn为En各设备分配方案的完工时间；BEnj为在En各设备分配方案中的第j台设备启动时间；TEnj为在En各设备分配方案中第j台设备从启动到关停的时间；Bik为第i项工序的第k项前序工序的开始时间；Bi为第i项工序的开始启动时间；Sik为第i项工序的第k项前道工序的标准工时；BE(i+1)j为第j台设备上排列的第i+1项工序的开始时间；BEij为第j台设备上排列的第i项工序的开始时间；SEij为第j台设备上排列的第i项工序的标准工时；Bi(qr)为第q个工件的第r项工序的开始时间；Si(qr)为第q个工件的第r项工序的标准工时；Bi(q(r+u))为q个工件的第r+u项工序的开始时间。

二级嵌套混合算法流程如图2所示，其基本思路是：发挥遗传算法求解“分配问题”和蚁群算法求解“排序问题”的优势。一级优化采用遗传算法求解工序的设备分配方案，二级优化采用蚁群算法求解与设备分配方案对应的工序最优排序，将一级优化结果作为蚂蚁的约束条件输入到二级迭代过程，将二级优化结果作为适应度信息反馈给一级迭代过程，从而形成完整的二级嵌套循环迭代过程。

图2 二级嵌套混合算法流程图

2 面向设备分配的改进遗传算法

2.1 改进的编码策略：基于工序的整数编码策略

采用遗传算法求解作业调度问题，如何将问题的方案转换为按一定规则编码表达的染色体是关键，好的编码方式既可以完整表达方案，又可避免信息冗余，从而降低时间复杂度和空间复杂度。以图 1为例，若使用传统的二进制编码，个体的编码长度为 7×33位的染色体，见表 1。表1存在大量编码资源冗余，如：与 A类设备不匹配的工序所对应的“基因位”数值必须为0，该基因位的存在，占用了信息资源，但在迭代过程中并没有作用，造成了编码资源冗余，可导致搜索效率大幅度下降。

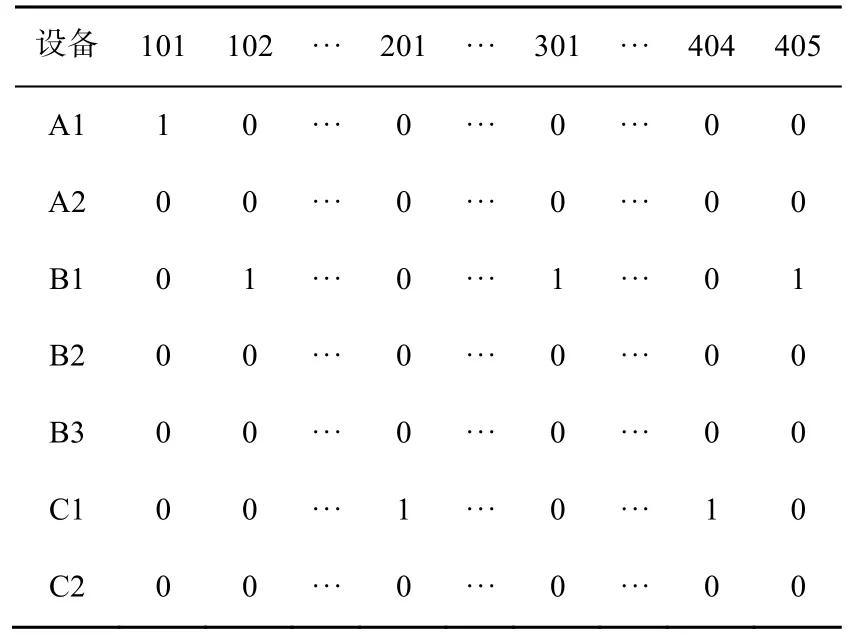
表1 一种传统的表达设备分配的编码方式

根据设备匹配约束，对编码方式进行改进，可大幅度节省编码资源。其改进方式如下：

首先，根据图 1，建立各类设备的工序集合，见表2，其中，设备号中ε是一个符号变量，表示该类设备编号：εaϵ{ε|ε=0,1}，εbϵ{ε|ε=0,1,2}，εcϵ{ε|ε=0,1}。

例如：当εa=0，表示选择设备A1；当εb=2，表示选择设备 B3。当要求在该类设备上进行加工的工序时，常规数字为工件号，下角标数字为工件相应的加工序号。例如 11表示工序 101，210表示工序210。

表2 设备工序集

其次，将上述待加工的工序按表中 A，B，C 3类设备的顺序排列成一个 33位的编码序列，如图3所示，编码的设计变量X={X1,X2,···,X33}，表示设备分配方案，Xi为第i个基因位上的值。

Xiϵ {Xi|X1～9=εa, X10～23=εb, X24～33=εc}

图3 染色体编码源基因位

例如：X1～90 1 1 0 0 0 0 1 1，X10～231 0 1 2 2 2 0 1 2 0 0 1 1 2，X24～330 1 1 0 0 1 1 0 0 1，是一个根据上述编码策略进行编码的染色体，X3=1表示工序 109分配至 A2；X14=2表示工序 203分配至B3；X32=0表示工序403分配至C1。该个体解码得到的局部分配方案见表3。

表3 局部设备分配方案

以这种改进的编码方式，可以得到一个仅有33位的编码方案，相比传统二进制编码方式，使染色体长度缩短至原来的 1/7，避免了编码串中因无用基因位的占用导致的编码资源浪费问题，使搜索过程更有效率。

2.2 改进的交叉策略：基于设备类型的多节点交叉策略

交叉操作是产生新性状的主要途径，编码策略是否可行，取决于该编码策略对应的交叉操作是否可行，或者是否有基于该编码策略的可行的交叉策略。在本编码策略中，由于每一个基因位均有确定的取值范围，如图3所示，在设备上分配的工序数并没有限制，交叉运算本质上是等位基因值的互换，经过交叉运算之后，得到的新个体一定满足约束条件。

例如，有2条染色体：

P1：[101100111 00210110010022 0011101001]

P2：[101000100 10221100110112 1000101011]

由于染色体中X10～23的取值可为 0，1，2，X1～9和X24～33的取值可为0，1，所以，在任意对等位置互换后，依然满足以上取值条件，得到的新个体依然是可行解。然而，该交叉方法存在交叉不充分的问题：任选一个节点进行分段交叉，实际上只有一类设备上可能产生新的分配方案，另2类设备的方案未有变化，如：P1和P2在第12个基因位进行交叉，得到：

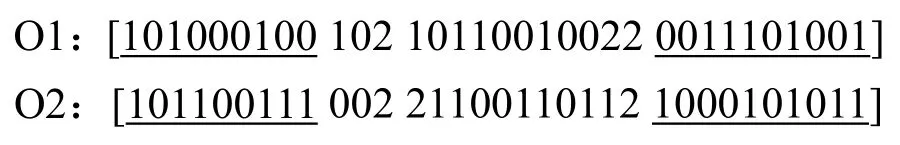
可以看出，新产生的个体O1和O2中，在A类和C类设备上的分配方案并没有改变，这使得交叉产生新性状的效率很低，本研究采用多点交叉，以避免这一问题，即：对3类设备均选择交叉点，分别在设备类别对应的3个区间进行交叉运算。具体方法是：分别产生3个[0，1]区间的随机数，将[0，1]分为段数等于可交叉位置数量的等步长区间，在随机数出现的区间对应的位置进行交叉互换，例如：3个随机数为0.42，0.78，0.28，第一类设备有8个交叉节点，0.42∈[3×1/8，4×1/8]，即处于第 4区间，则将前9位基因在第4个节点进行截断交叉；0.78∈[10×1/13, 11×1/13]，则将 10～23 位基因在第11个节点进行截断交叉；0.28∈[2×1/9，3×1/9]，则将24～33位基因在第3个节点进行截断交叉，得到新的个体：

可以看出，2个新个体在 3类设备的分配上均产生了新性状，即，产生了3类设备分配方案的新的可行解，从而扩展了搜索空间，提升了搜索效率。

2.3 改进的变异策略：设备类别区间内基因互换

变异策略是否可行，同样取决于变异后的个体是否可行。由于不同类别的设备数量可能不同，因此，在不同的基因段，取值范围也不同，常规的变异操作可能导致出现不可行解。为避免这一问题，本研究采用设备类别区间内小概率基因互换策略。

首先产生3个[0，1]范围内的随机数，第一个随机数用于确定选择哪一个个体进行变异操作；然后将[0，1]分为等步长的33个区间，采用与交叉策略同样的方法，确定2个随机数分别落在 1～9，10～23，24～33哪个区间段。如果 2个随机数落在同一区间段，则需对2个基因位的值进行互换，如果落在不同的区间段，则不进行变异操作。由于变异操作是小概率操作，所以在有的迭代过程中不进行变异操作，并不影响搜索的收敛性。

3 面向工序排序的基于逆向遍历的蚁群算法

3.1 逆向遍历形成可行路径的方法

采用蚁群算法求解工序排序问题，每一个个体即为工序可行路径。对于主工序图，每一个蚂蚁个体可逆向将所有工序遍历一次后再倒序排序，得到一条相应的满足先后关系的工序路径。由于工序有串行、并行和嵌套关系，所以蚂蚁个体在逆向遍历时会有多种选择方案，这就形成了初始蚁群。例如：对于图1中工件1的工序图，在其中一种路径选择完成逆向遍历：109→107→108→106→103→105→104→102→101，再倒序排序：101→102→104→105→103→106→108→107→109，这就形成了一只蚂蚁个体的完整路径。

3.2 路径确定的前提下单个蚂蚁最优解的求解方法

遗传算法所得到的设备分配方案，作为初始条件传递给蚁群算法，通过逆向遍历再倒序排序的方式，可以确定设备上工序加工的先后顺序。只要工序启动加工的时间，满足作业调度问题的各种约束条件，则其解就是一个可行解，即在设备上的工序分配方案以及加工顺序确定的情况下，依然可以得到很多可行解，因此，需要从所有可行解中找出最优解，作为蚂蚁播洒信息素的依据。

在逆向遍历中产生满足以上条件的众多加工路径中，一定可以确定一个使设备利用率最高的最优排序，在甘特图中表现为设备等待时间最短，该排序就是这一加工路径的最优排序。换言之，逆向遍历产生蚁群，其中每一个个体一定有一个使总完工时间最短的最优解，其对应的总完工时间就可以作为此蚂蚁路径上的信息素分配依据。以工件1为例，如果遗传算法的设备分配方案是 3类，加工工序分别分配在 A1，A2，B1，B2，B3，C1，C2上，根据 3.1节中形成的蚂蚁路径，可以得到设备上分配的工序排序，见表4。并通过调整工序启动时间回避工件独占约束、前序工序约束等约束，得到唯一的最短加工时间的调度方案，图4为甘特图，其最短加工时间为 95，即作为该蚂蚁路径的信息素播洒依据。

表4 设备上的工序排序

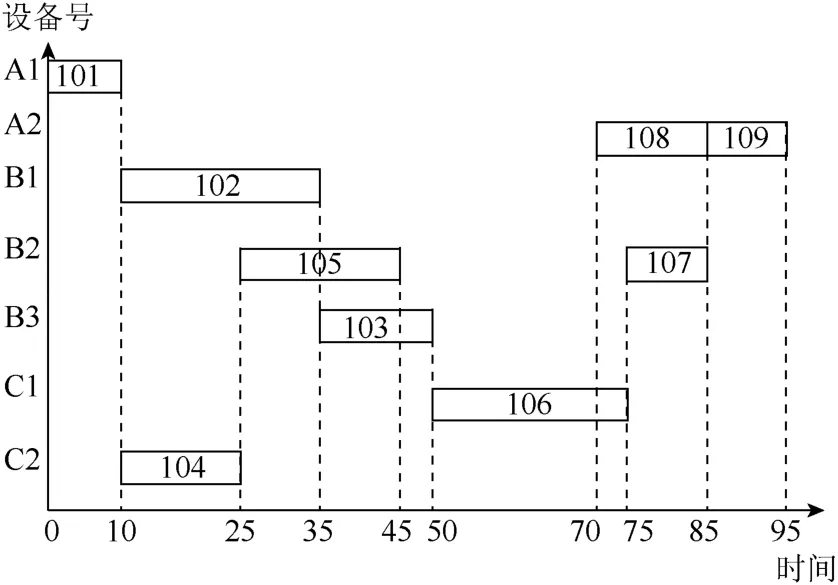
图4 表4条件下工件1的唯一最短加工时间对应的调度方案的甘特图

3.3 信息素播洒与更新策略

信息素分配有多种方法，对任意蚂蚁αμ(μ= 1 ,2,… ,ϑ)，有对应的最优解(最优排序)和与其对应总完工时间cμ，则该蚂蚁相应的每段路径上分配的信息素浓度τμ=1/cμ。因此，单个蚂蚁完成对应最优路径全程的时间越短，其每段路径上分配到的信息素浓度越高，对于2个节点i和j之间有

其中，为初始蚁群完成第一次遍历后节点i与j之间的信息素浓度。当初始蚁群中所有蚂蚁都完成了各自对应的路径，就可以计算出与初始种群对应的各路径上的信息素浓度。各条路径上的信息素可更新为

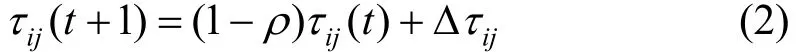
其中，Δτij=；ρ为信息素挥发系数；τij(t+1)为更新后的节点i与j之间的信息素浓度；Δτij为节点i与j之间的信息素浓度增量。

此时，产生新蚂蚁，并根据信息素浓度来选择路径，蚂蚁aμ可根据的大小，确定移动方向

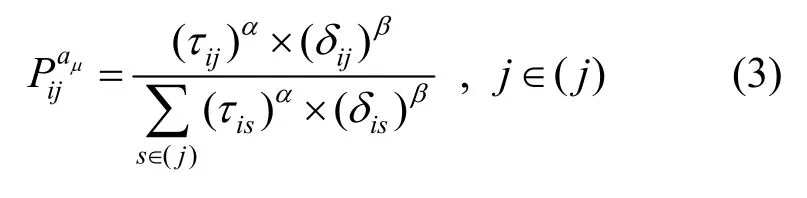
当绝大部分蚂蚁都选择同一条路径时，即得到了最优路径，输出对应的最短完工时间，作为个体的适应度传递到遗传算法模块，从而形成了由遗传算法与蚁群算法相互嵌套的循环迭代过程。

4 对比试验研究

虽然目前有较多关于作业车间调度问题的研究，但研究仍集中于中、小规模、以串行工序为主的问题[20-21]。对于有一定规模的存在包括嵌套关系的调度问题，研究还较少，目前还没有公认的标杆问题。在前期的研究中[22]，采用二级嵌套蚁群算法(二级求解均采用蚁群算法)，对包含主要以串联关系组成的19个工序的案例进行了研究，该案例仅包含少量的嵌套工序。本文主要针对规模更大、关联约束更复杂的情况(包含较多的二级嵌套关联关系)。图 1包含 4个工件、33道存在串行、并行、嵌套关系的工序、3类共7 台设备(A1，A2，B1，B2，B3，C1，C2)，以图 1为研究案例，分别采用遗传算法、蚁群算法、二级嵌套蚁群算法、遗传算法与蚁群算法相结合的二级嵌套混合仿生算法，进行对比试验研究。

单独采用遗传算法：

采用遗传算法求解案例，经过20 000次迭代，迭代过程无收敛特征，在迭代中，最优解的目标函数值在245附近，工时利用率仅为30.95%，最优解如图5所示。

(1) 单独采用蚁群算法。采用蚁群算法进行多次求解试验，偶尔会出现收敛特征，但出现收敛特征的几次试验中，所得到的解有较大差异，说明搜索过程陷入了局部最优。设置停机准则：①无收敛特征，则进行20 000次迭代后停机，并输出迭代中的最优解；②有收敛特征，输出停机时所得到的解。经过50次算法试验，所得到的最优解的目标函数值为 240，工时利用率仅为31.52%，最优解如图6所示。

图5 单独采用遗传算法所得最优解的甘特图

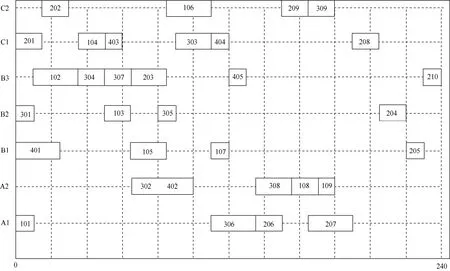
图6 单独采用蚁群算法所得最优解的甘特图

(2) 采用二级嵌套蚁群算法[22]求解。迭代1 800次左右，即满足停机准则，求解有比较高的搜索效率，但优化程度较低，如图7所示。最优解的目标函数值为220，工时利用率仅为34.17%。

(3) 采用遗传算法与蚁群算法相结合的二级嵌套混合仿生算法。经过约1 000次迭代后，即出现收敛特征，经过约5 000次迭代，得到最优解，如图8所示。最优方案所对应的总加工时间为155，设备工时利用率为 53.79%，对于复杂调度问题而言，该工时利用率较高。

表5为4种算法的对比试验结果，表明了本文方法的有效性和优越性。

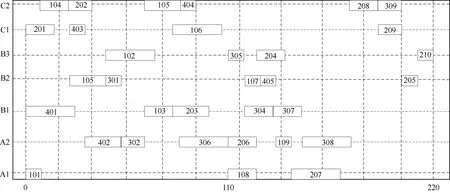
图7 二级嵌套蚁群算法所得最优解的甘特图

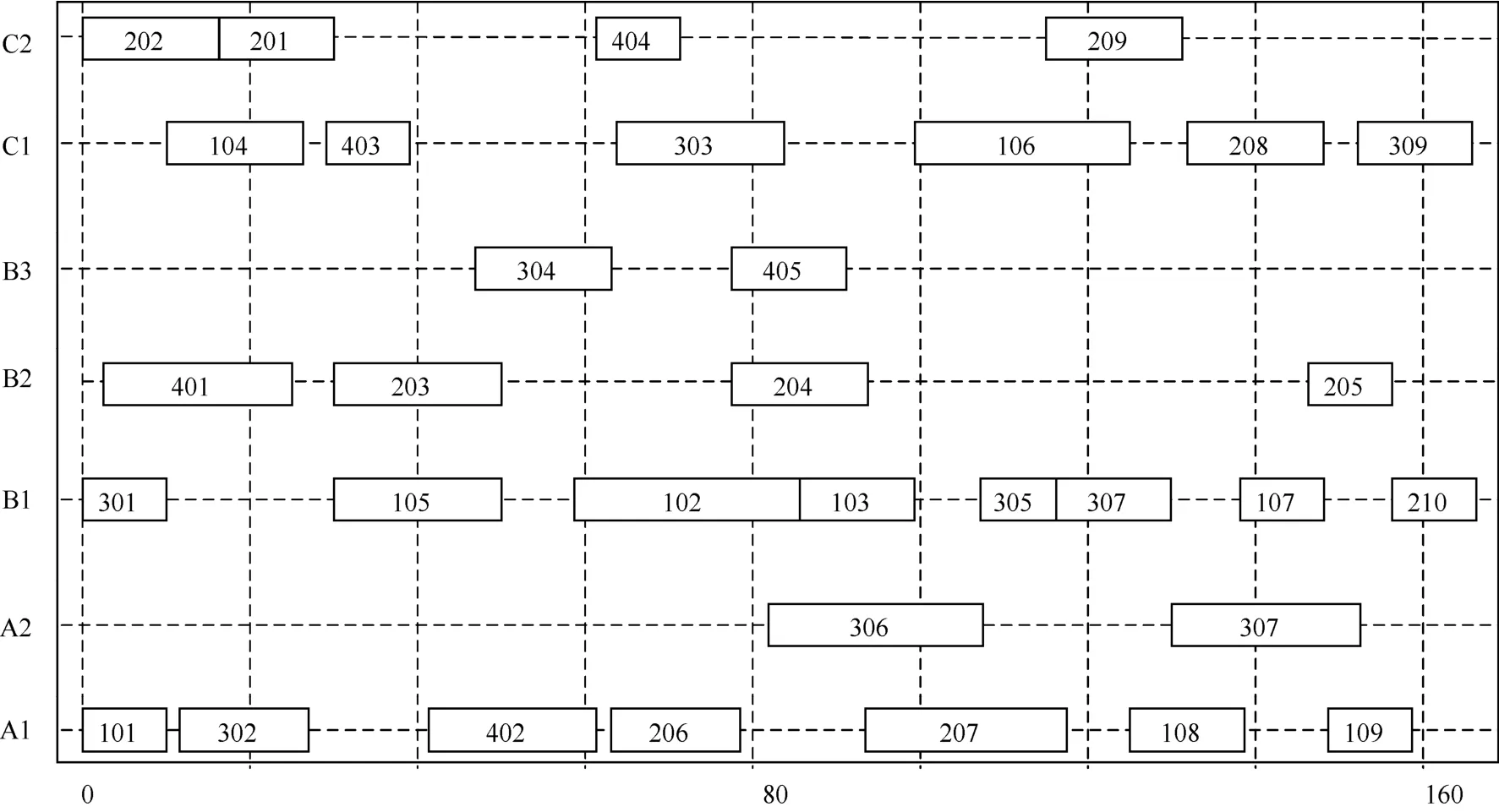
图8 二级嵌套混合算法所得最优解的甘特图

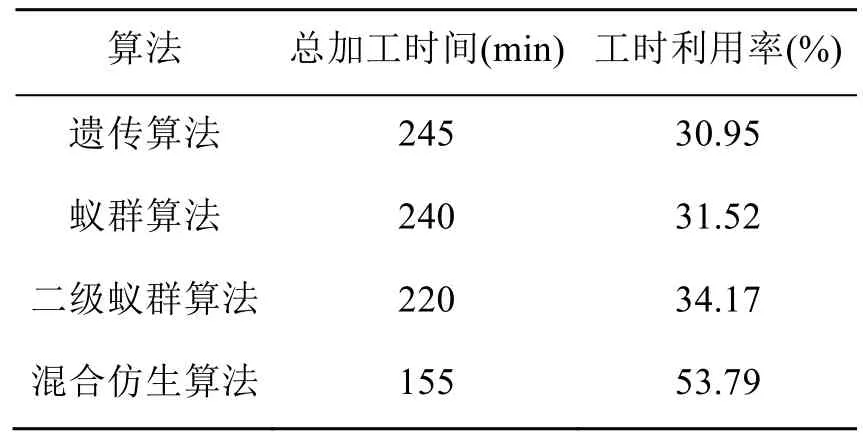
表5 算法对比试验结果

5 结 论

求解包含复杂关联约束的JSSP，目前依然是难点问题，相关研究成果还比较少。本研究将该难点问题分解为：“设备分配”和“工序排序” 2个相互耦合的子问题，分别发挥遗传算法和蚁群算法各自的优势来求解这2个问题，并通过一系列改进策略，构造了集成遗传算法与蚁群算法于一体的二级嵌套混合算法。对于有一定规模、包含嵌套复杂关联约束的JSSP研究案例，采用二级嵌套混合算法得到的解，工时利用率为53.79%，是一个比较满意的解，与单独的遗传算法、蚁群算法、或二级嵌套蚁群算法相比，有更高的可靠性和优化程度。

当然，由于对于包含复杂关联约束的 JSSP的研究还非常少，目前还没有公认的标杆问题，也没有公认的较成熟的算法。本文通过理论分析和案例研究表明：针对包含复杂关联约束的JSSP，所提出的方法具有有效性和相对的优越性，为该类问题的进一步研究提供了新思路和新方法。