超短基线安装误差对定位精度影响分析及其标定技术研究
2020-03-19童金武徐晓苏翁铖铖
童金武,徐晓苏,张 涛,李 瑶,翁铖铖
(东南大学仪器科学与工程学院微惯性仪表与先进导航技术教育部重点实验室,南京 210096)
0 引言
水下声学定位系统根据其基线的长短将水声定位系统分为超短基线(Ultra-Short Baselines,USBL)、短基线(Short Base Line,SBL)和长基线(Long Base Line,LBL)[1]。USBL由于其基阵尺寸小、使用便携等优点被广泛应用于水下目标定位作业[2]。由于单一的导航手段难以满足目前水下作业任务所提出的长距离、高精度导航定位要求,水下导航广泛采用捷联惯性导航系统(Strapdown Inertial Navigation System,SINS)/LBL、SINS/SBL、SINS/USBL、SINS/DVL(Doppler Velocity Log)等方式进行组合导航[3-6]。在USBL定位系统的诸多误差源中,声学基阵安装误差是其重要误差源之一[7-8]。有文献表明,在定位精度为0.5%的USBL定位系统中,1°的航向安装误差角将导致1.7%倍斜距的定位误差[9],因此USBL定位系统在使用前必须进行高精度校准。为了避免在每次定位前对USBL安装误差角进行重复校准,目前现有SINS/USBL组合导航系统广泛采用一体化设计结构。2005年唐秋华首次提出了采用最小二乘法解算USBL安装误差角[8,10]。郑翠娥等在现场试验中验证了最小二乘法估计USBL安装误差角方法的可行性,经该方法补偿后的USBL定位系统精度可达到斜距的5‰[9,11]。中国台湾陈信宏、杜广文等提出了采用多次绕行法构造绕行半径差对安装误差角进行估计,但该方法要求先确定母船环绕轨迹的圆心的位置才能得到绕行半径的精确值,难以在实际工程中直接应用[12]。杜广文也在其硕士学位论文中研究了母船沿直线航行的USBL安装误差标定方法[13],陈信宏等于2013年在实验中验证了母船直线航迹法的可行性[8]。2018年,基于双应答器的USBL标定方法进行USBL安装误差角的高精度标定[1],提高了USBL安装误差角的标定精度,但是该方法要求双应答器的连线与天向坐标轴平行,因此适用于USBL设备生产商对USBL安装误差进行出厂标定。在现有的安装误差角标定技术中,通常将安装误差角作为状态量,通过迭代的方法不断对其进行修正,将修正量小于某个设定的阀值作为算法迭代结束的条件[8]。该方法的不足之处在于,若前后两次安装误差角的估计值都收敛在同一个伪点时,其安装误差的修正量可能会小于预设定的阀值,导致迭代结束,安装误差角估计出错。本文将以对一体化SINS/USBL系统中USBL安装误差进行高精度校准为需求背景,深入分析USBL安装误差角对USBL水平定位精度的影响,开展对USBL安装误差角标定技术的研究。根据分别采用LBL、USBL方法对目标应答器的定位解算值及USBL声头的位置值构造2个共端矢量,通过对这2个矢量的相关性判断达到控制USBL安装误差角估计精度的目的。
本文结构安排如下,在引言部分介绍了USBL及其安装误差标定的研究现状;第1节对USBL定位系统原理进行简要说明;第2节采用数值仿真的方法对USBL安装误差角在其水平定位精度的影响进行评估;第3节对本文设计的基于单应答器双矢量重构的基阵安装误差角高精度标定算法进行详细阐述。这也是本文的主要贡献。第4节对本文中所设计的算法进行水下实验验证与分析,第5节是总结。
1 USBL定位系统原理
1.1 USBL坐标系统
本文需要用到多个坐标系统:USBL基阵坐标系(简称u系,OuXuYuZu),USBL在此坐标系下对目标进行定位解算,定义如图1所示,基元1、2分别位于X轴的正、负半轴上。基元3、4分别位于Y轴的正、负半轴上,发射声头位于坐标原点,即基阵的声学中心。
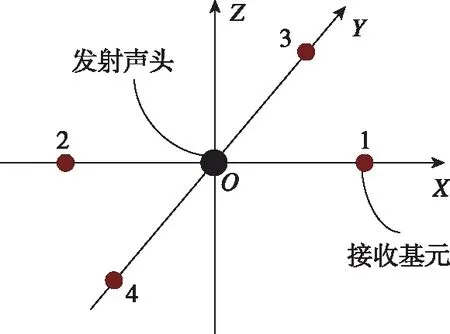
图1 USBL声学基阵坐标系示意图Fig.1 Schematic diagram of USBL acoustic array frame
载体坐标系(简称b系,ObXbYbZb),Y轴正方向指向船艏向,X轴正方向指向右舷,Z轴垂直于xoy平面,竖直向上为正方向。USBL声学基阵刚性安装在载体上,其姿态可以由姿态基准测得。USBL声学基阵安装在基座下方,朝下倒扣安装。理想情况下,基座坐标系与USBL声学基阵坐标系完全平行;工程实践中,b系与u系对应的坐标轴之间很难做到完全平行,他们之间在航向、纵摇、横摇轴方向存在大小为α、β、γ的安装误差角(其中也包括由器件加工引起的角度偏差),如图2所示。
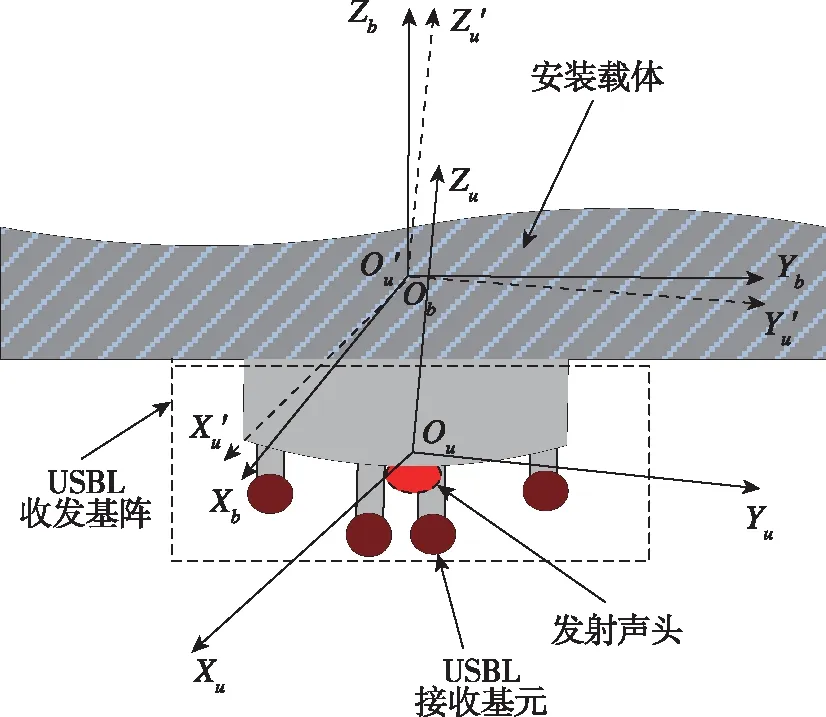
图2 USBL基阵坐标系、载体坐标系示意图Fig.2 Schematic diagram of USBL acoustic array frame and carrier frame
为了得到被定位目标的绝对位置还需要用到全局坐标系(简称g系,OgXgYgZg),g系采用WGS-84 坐标系。另外将地理坐标系作为导航坐标系(简称n系,OnXnYnZn),其坐标原点位于USBL声头的几何中心上,X轴指东向,Y轴指北向,Z轴指天向。为了方便误差分析,还引入了辅助坐标系 (简称a系,OaXaYaZa),坐标原点位于目标应答器的天向连线与水平面的交点,X轴指东向,Y轴指北向,Z轴指天向。本文中所有涉及载体姿态角及USBL安装误差角的方向定义如下,航向角:北偏东为正;纵摇角:北偏上为正;横摇角:东偏上为正。
1.2 USBL基本定位原理
超短基线定位系统由USBL收发基阵上多个接收基元共同接收来自被定位目标的水声信号,并通过相位差解算得到接收声线相对于USBL基阵的方向角值。用方向角结合被定位目标的深度或距离对目标进行位置解算,得到目标相对于USBL收发基阵的位置[14]。超短基线的定位解算模型主要有:基于距离与方向角值的USBL定位模型,基于深度与方向角值的USBL定位模型,基于深度与相位比的定位模型等。图3所示为基于距离与方向角定位解算模型的USBL定位原理示意图。
USBL定位系统由收发基阵和水下应答器组成,如图3所示,发射声头位于收发基阵的几何中心。T为应答器,R为应答器T与声头的距离,r为应答器与声头之间的水平斜距,显然
(1)
(2)
其中
(3)
其中,xu、yu、zu为目标应答器在USBL基阵坐标系下的坐标。相位差产生的原因是从目标应答器到各基元之间存在距离差所致,其原理如图4所示。
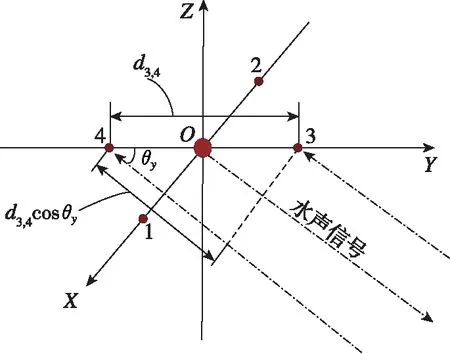
图4 USBL相位差示意图Fig.4 Schematic diagram of USBL phase difference
基元1、2之间的相位差为
(4)
同理,基元3、4之间的相位差为
(5)
其中,d为基元间距,∠θx和∠θy为水声信号的方向角。λ为水声信号波长。在图3中
(6)
(7)
式(2)、式(6)、式(7)为基于距离与方向角模型的USBL声学定位基本解算公式。
对式(6)取全微分得到
(8)
其中,Δφ1,2为基元1、2之间的相位差测量误差,Δλ为波长误差,ΔR为测距误差,Δd为基元间距误差。当各误差项相互独立时,分析斜距相对定位精度的均方误差如下所示
(9)
式(9)中,等式右边第二项误差主要是测距误差和基元间距误差,如果等效声速、时延和基元间距测量值比较精确的情况下,其对定位精度的影响可忽略不计[14]。基元间的相位差测量误差是USBL水声定位系统的主要误差源,而安装误差是导致相位差误差产生的重要原因之一。
2 安装误差角对USBL定位精度影响分析
假设载有USBL的母船绕水下目标应答器沿圆形轨迹航行,如图5所示,显然,目标应答器在辅助坐标系O-XaYaZa中的坐标为(0,0,-h)T。在ti时刻目标应答器T在USBL坐标系下坐标为(L,0,-h)T。
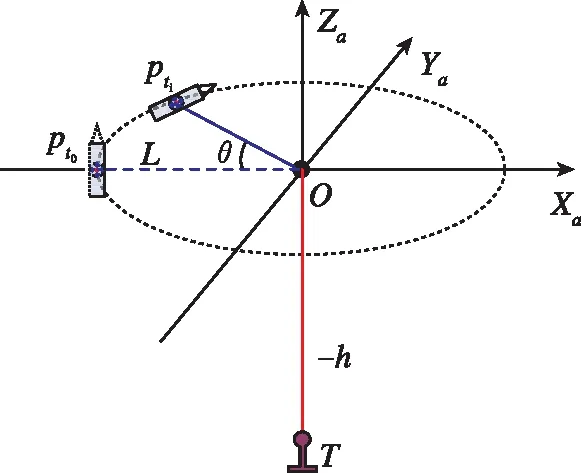
图5 母船绕行示意图Fig.5 Schematic diagram of the carrier ship travelling along a circular trajectory
当USBL载体坐标系ObXbYbZb与声学基阵坐标系OuXuYuZu之间存在航向安装误差角α时,坐标转换矩阵为
(10)
则目标应答器T在声学基阵坐标系OuXuYuZu的坐标为
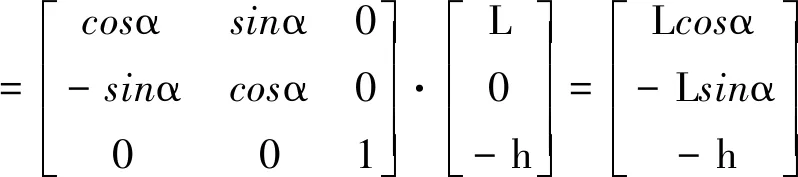
(11)
为了分析航向安装误差对目标应答器的定位影响,计算u系下由航向安装误差引起的对目标应答器的定位误差为
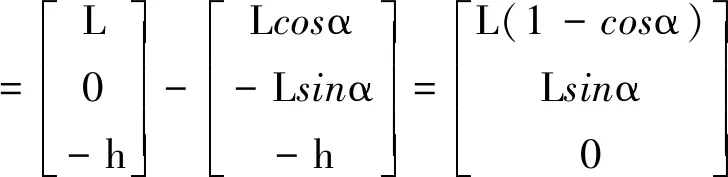
(12)
不考虑其他误差的情况下,由式(12)可知,USBL航向安装误差角α产生X轴方向上的定位误差为
δPb,u(x)(a)=L(1-cosα)
(13)
Y轴方向上的定位误差为
δPb,u(y)(a)=Lsinα
(14)
由航向安装误差角导致的水平定位误差为
(15)
同理,由纵摇和横摇安装误差角导致的水平定位误差分别为
=hsinβ
(16)
=L(1-cosγ)-hsinγ
(17)
其中,L为母船的绕行半径,h为目标应答器的深度,α、β、γ分别为USBL航向、纵摇、横摇方向的安装误差角度值。
为了研究安装误差角对USBL水平定位精度的影响,对其进行数值仿真。参数设置如下,被定位目标应答器T水下深度值ht=1000m,USBL收发器与辅助坐标系的坐标原点之间的水平距离L分别取500m、1000m和1500m,航向误差角α=1°,水平定位误差如图6所示。
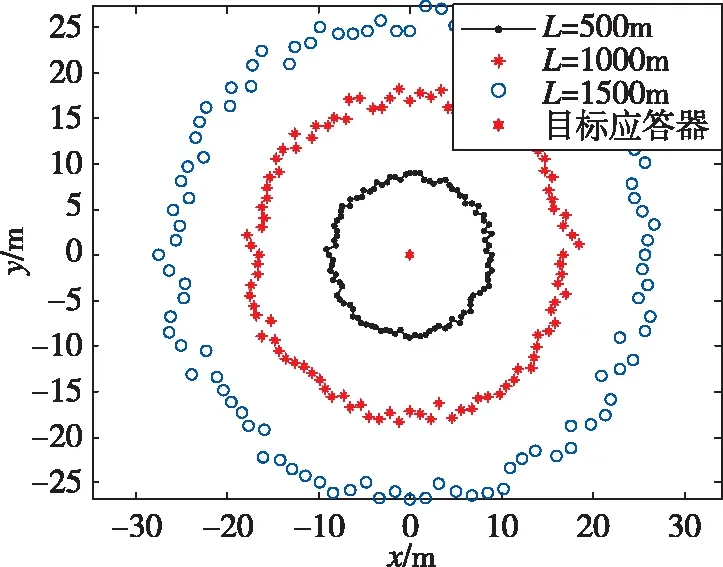
图6 USBL航向安装误差角在不同定位距离条件下导致的水平定位误差Fig.6 Horizontal positioning error caused by heading misalignment error angle of USBL under different positioning distance
从图6可以看出,USBL水平定位误差的大小与目标距离有关,距离越大,误差越大。在1000m的水平距离内,1°的航向安装误差角可导致17.43m的水平定位误差。当航向安装误差角a分别取0.01°、0.1°、0.5°和1°时,水平定位误差如图7所示。
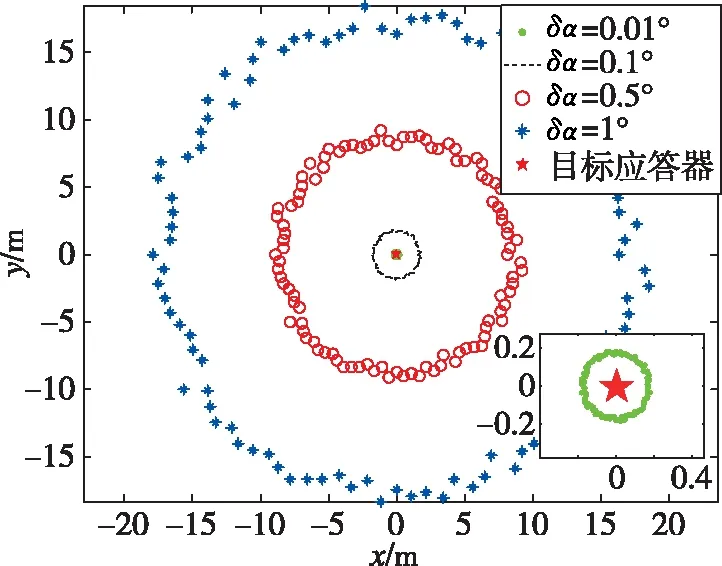
图7 不同量级的USBL航向安装误差角对USBL水平定位精度影响Fig.7 Influence of USBL heading misalignment error angle of different magnitude on USBL horizontal positioning accuracy
从图7可以看出,在1000m水平距离内1°和0.5°的USBL航向安装误差角分别导致17.2m和8.648m的水平定位误差;当安装误差角为0.1°和0.01°时,USBL航向安装误差角分别导致0.172m和0.017m的水平定位误差。
在同样的仿真条件下,1°的纵摇和横摇方向的安装误差角所导致的水平定位误差仿真结果如图8和图9所示。
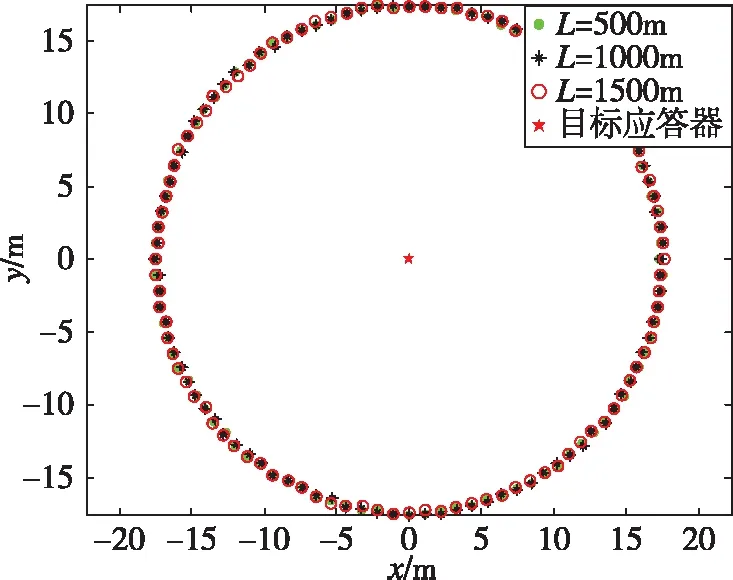
图8 USBL纵摇安装误差角在不同定位距离条件下导致的水平定位误差Fig.8 Horizontal positioning error caused by pitch misalignment error angle of USBL under different positioning distance
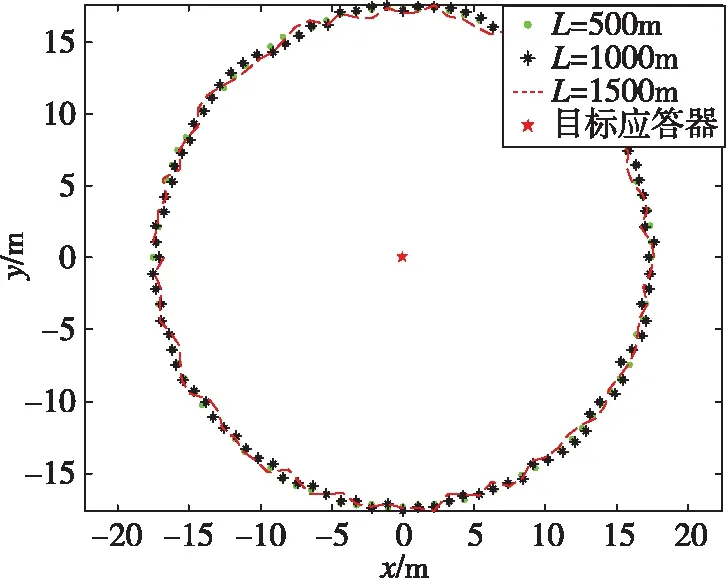
图9 USBL横摇安装误差角在不同水平定位距离条件下水平定位误差示意图Fig.9 Horizontal positioning error of roll misalignment error angle of USBL under different horizontal positioning distance
从图8和图9可以看出,纵摇和横摇安装误差角对USBL水平定位精度的影响对水平距离不敏感,由式(16)和式(17)可以看出,其定位精度主要受目标深度的影响。
从上述理论分析和仿真可知,USBL安装误差角对USBL水平定位精度的影响较大,在定位前必须对其进行安装误差校准。
3 基于单应答器双矢量重构的基阵安装误差角高精度标定方法
3.1 安装误差估计总体方案设计
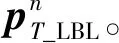
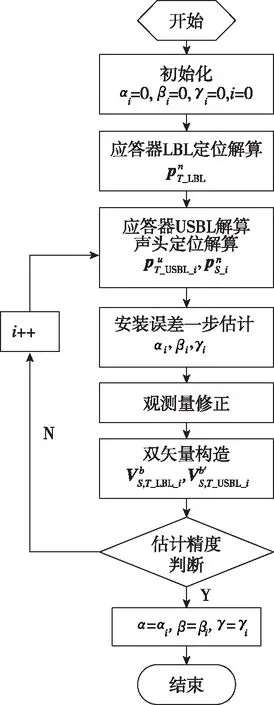
图10 USBL安装误差估计总体方案原理图Fig.10 Schematic diagram of the angular misalignment error estimation
3.2 USBL安装误差角一步估计
由于安装误中平移误差对USBL定位精度影响较小,而角度偏差对USBL定位精度影响大。在本文中,USBL安装误差不考虑位置平移误差,只研究安装误差角的估计。
在考虑USBL坐标系与载体坐标系之间存在安装误差角时,水下目标应答器的位置在导航坐标系下的投影可简化为
(18)
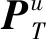
(19)
(20)
(21)
(22)
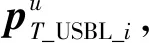
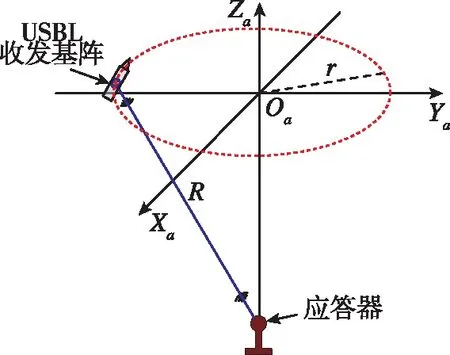
图11 母船航行示意图Fig.11 Schematic diagram of carrier ship sailing
为了加快估计的收敛速度,图10中的安装误差估计模块的一步估计过程是按航向、纵摇、横摇的次序分别对3个方向的安装误差角进行一步估计得到αi、βi、γi值。
步骤1:对αi求解
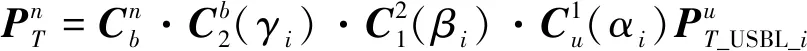
(23)
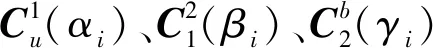
步骤2:对βi求解
如式(23)所示,在估计βi的过程中将ai置为本次估计值。第1次解算βi时,γi置为0,第i次(i>1)求解时,γi=γi-1,即使用上一次的解算值。βi为满足式(23)的最优解。
步骤3:对γi求解
如式(23)所示,解算γi时将αi、βi置为本次解算值,γi为满足式(23)的最优解。
3.3 USBL安装误差角补偿及双矢量重构
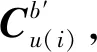
(24)
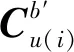
(25)
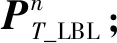
用上述3个值构造2个矢量序列
(26)
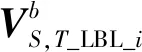
(27)
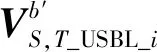
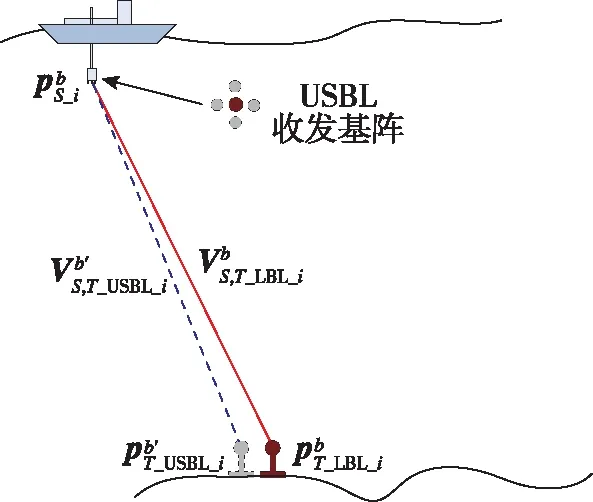
图12 双矢量示意图Fig.12 The schematic of dual vector
3.4 USBL安装误差角估计精度控制
理想情况下,不考虑安装误差等其他误差的影响,USBL对水下目标应答器的定位解算值与采用高精度LBL方法的定位解算值在误差范围内具有高度一致性。本文根据此原理对不断重构的双矢量进行相关性判断,实现对USBL安装误差估计精度的控制。
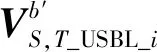
(28)
εth为阀值,该值的确定与目标的深度、水声环境等诸多因素有关,此值需根据试验现场条件及经验设定,在本文中εth取0.005。当Δ值小于所设定的εth时,说明经过USBL安装误差补偿后的目标应答器的定位解算值在误差范围内与高精度的LBL方法的定位解值精度一致。此时安装误差估计结束,输出安装误差的最终估计值α、β、γ。
4 实验与验证
为了验证本文提出的基于双矢量重构的USBL定位算法的定位性能,2018年9月在长江进行了水下试验。本次试验中,目标应答器采用9V电池供电,接收频率为22~26kHz,发送频率为18~22kHz可选,外观如图13所示。

图13 目标应答器Fig.13 Target transponder
USBL接收基阵采用四阵元平面阵结构,4个阵元位于声学基阵的水平轴上,发射声头位于4个基阵的几何中心,信号频率为18k~26kHz宽带扩频信号,其结构如图14所示。

图14 USBL收发基阵Fig.14 USBL transceiver array
收发基阵与连接杆之间刚性连接,竖直向下安放。收发基阵放置于水下1m深处,整个USBL收发装置位于母船的右舷。距离声头1.8m处安装有高精度捷联姿态基准,为载体提供高精度姿态,如图15所示。

图15 USBL安装布局图Fig.15 USBL misalignment layout
试验1 水下应答器高精度定位
母船的出发点为原点,应答器的水平位置通过高精度实时动态定位(Real-Time Kinematic,RTK)测得,RTK定位精度为±(8+10-6×D)mm,测得目标应答器相对于坐标原点的水平位置为X=-25.915m,Y=-6.087m。载有USBL定位系统的母船以25m左右为半径环绕目标应答器航行1圈,其航行轨迹如图16所示。
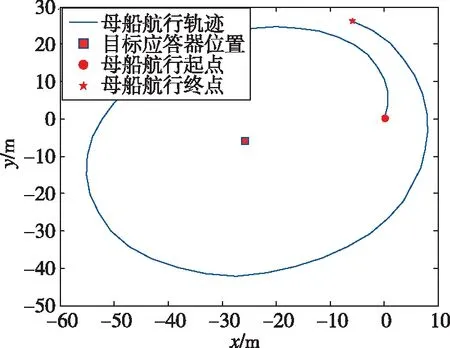
图16 母船航行轨迹示意图Fig.16 The trajectory of carrier ship
图17所示为LBL方法与参考真值的水平定位误差,可以看出,母船采用长基线方法绕行1周,经过5次迭代计算后其定位水平精度≤0.5m。
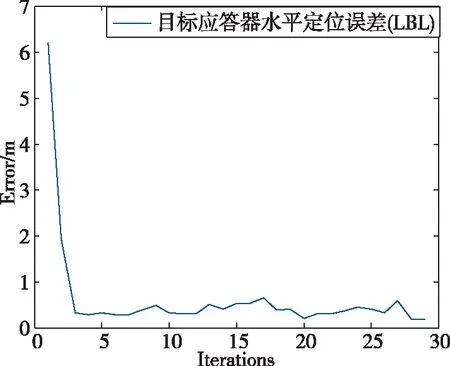
图17 目标应答器的水平定位误差Fig.17 The horizontal positioning error of transponder by LBL method
试验2USBL安装误差校正
在试验1中母船绕行1周就得到了水下目标应答器的值,实验2中仍采用实验1中的轨迹及声头的位置测量值,与此同时对水下应答器进行USBL定位解算。图18中红色小圈是标定前USBL系统对水下目标应答器的定位解算结果,星形是安装误差校正后USBL的定位解算结果,五角星为目标应答器的参考真值。
从图18可以看出,由于存在较大的安装误差,致使USBL水平定位误差为10~20m,而经过安装误差校准后,对目标应答器的定位解算结果明显收敛在一个较小的范围内。
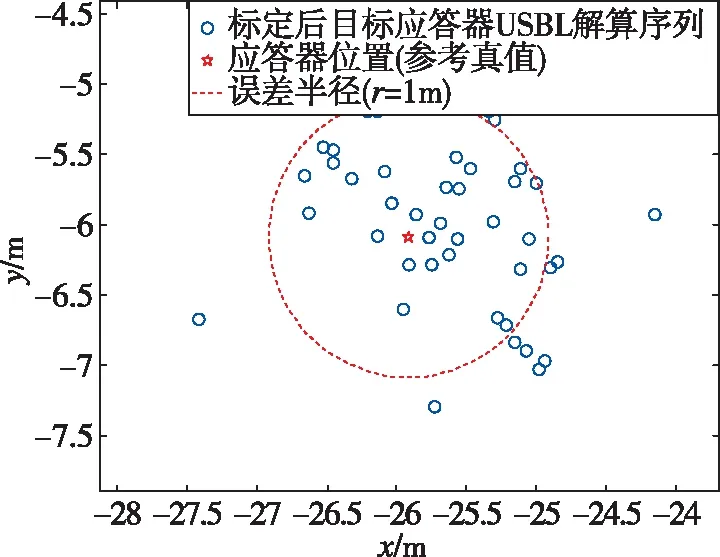
图19 安装误差补偿后USBL对目标应答器定位结果图Fig.19 The transponder positioning result by USBL method after misalignment error compensation
图19所示为安装误差补偿后USBL对目标应答器的定位结果图,从图19中可以看出,经补偿后,80%以上的目标应答器的水平定位误差≤1m。
5 结论
本文通过数值仿真的方法研究了USBL安装误差角对USBL定位系统定位精度的影响,并设计了一种基于双矢量重构的USBL安装误差估计算法,利用3个观测值构造2个矢量。通过对2个矢量的相关性进行判断实现对USBL安装误差角估计精度的控制,该方法从理论上有效避免了外部干扰对估计精度的影响。另外,本算法也为确定USBL安装误差角估计模块的迭代次数提供了理论的依据。实验表明,基于单应答器的双矢量重构方法对USBL安装误差角的估计精度较高。本文提出的算法对目标应答器的定位解算与USBL安装误差角的估计可以在一次绕圈中完成,操作过程简单,易于实现,具有重要的工程应用价值。
